逆誤差関数、誤差関数
逆誤差関数には、前述の逆誤差関数があるのですが、有効桁数を50桁程度で、１に近い値となると、ckの大きな配列の値を必要とするので、あまり実用的ではありません。
18桁程度の精度のものは、インターネットで公開されているプログラムをDelphiに変換してみました。
Extendedで17桁、Doubleの演算では15桁程度の精度が得られます。 逆誤差関数２ 逆誤差関数３
精度のが高い逆誤差関数の必要性はあまりないと思われますが、計算できないのも問題なので、演算に時間が掛かるのですが、誤差関数erf(z)を利用して逆誤差関数erfinv(y)を求めるプログラムを作成てみました。
erf(z)の計算時、z<2.4はテーラー展開z>=2.4は連分数の計算をしています。
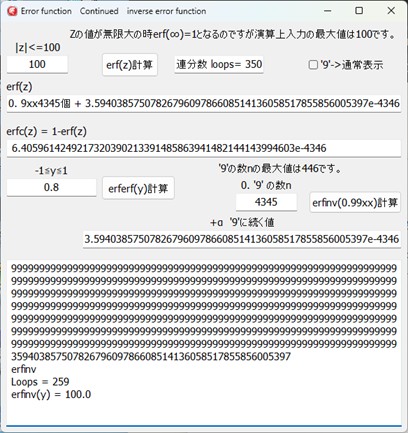プログラムはerf(z)のzの最大値は100、erfinv(y)の値は0.999・・9の9の連続値が最大4345個となっています。
erf(z)のzの値は、プログラムを修正すれば、もっと大きな値を与えることができます。
逆誤差関数erfinv(y)のyの値を9の個数+αで与える場合は、負数を与えることは出来ません。
yの値と、erfinv(y)の符号は同じになるので、問題ないでしょう。
'9'の個数で、yの値を与える場合、9に続く値の与え方として
0.0012345、1.2345e-3の様な場合は加算、345234の様に少数点がない場合9の後に続く値として0.9999345234の様に取り扱いされます。
'9'の数を0とすれば、通常の符号付き入力として取り扱われます。
erf(z)のzの値が大きくなると、erfinv(y)の計算時間は、非常に長くなります。
zの値が100になるような場合は、cpuの能力によりますが、遅いので数分、速いので数十秒必要とします。
y=0.99・・9の9値が50個程度のerfinv(y)の計算なら十数秒で計算出来るので問題ないでしょう。
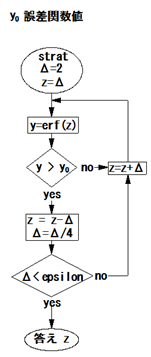逆誤差関数の計算方法は、単純な計算方法で、y=erf(z)のz=0の時yの値もゼロとなり、正比例することを利用します。
目標として当たられるのはyの値なので単純な近似計算を行います。
epsilonの値は、yの絶対値が0.1以下なら1e-200、0.1以上なら1e-80を与えます。
演算結果として50桁を得るためには、yの値が0.1以上なら1E-80で十分です。
0.1以下の場合、zの値が小さくなるので、epsilonの値を小さくする必要があります。
yの値に応じてepsilonの値を計算してあげた方が、計算時間を節約できます。
その時には、除算時の有効桁数も一緒に変更した方が良いでしょう。
プログラム
Biginteger & Bigdecimal の組み込み方は第１種ケルビン関数を参照して下さい。
main.pas
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, system.UITypes,
Vcl.Buttons;
type
TForm1 = class(TForm)
zEdit: TLabeledEdit;
calcBtn: TButton;
ansREdit: TLabeledEdit;
nEdit: TEdit;
OneMansEdit: TLabeledEdit;
Label1: TLabel;
Memo1: TMemo;
yEdit: TLabeledEdit;
invBtn: TBitBtn;
CheckBox1: TCheckBox;
n9Edit: TLabeledEdit;
p9aedit: TLabeledEdit;
inv9Btn: TButton;
Label2: TLabel;
procedure calcBtnClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure invBtnClick(Sender: TObject);
procedure inv9BtnClick(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses System.Character, Sub_big, Velthuis.BigIntegers, Velthuis.Bigdecimals;
const
ZINMAX = '100'; // |z|の入力最大値 有効桁数と収束判定値の関係での値
EPSC = '1e-500'; // 誤差関数収束反対値
// 除算有効桁数が不足し、収束判定値が大きいと演算結果が
// 1.0を超えます。
//------------------------------------------------------------------------------
// 演算時間 秒
// n8 9の数
function inversetime(n9: integer): double;
const
r = 0.911927968427609;
a = -5;
b = 8;
begin
if n9 = 0 then result := 1
else result := b * ln(n9 + 1) + a;
result := round(result);
end;
//------------------------------------------------------------------------------
// 数値の後ろのゼロ消去
function ZeroErase(s : string): string;
const
EP = 'e';
ZC = '0';
dt = '.';
var
c : char;
i, j, k, l : integer;
begin
l := length(s); // l文字長さ
j := 1; // j=1初期化
for i := 1 to l do begin // 一文字目から
c := s[i]; // 一文字取り出し
if c = EP then begin // 'e'だったら
j := i - 1; // eの前の文字No
break; // ブレーク
end;
j := i; // 'e'がなかったらj=i
end;
result := ''; // ''設定
if j < l then begin // jが文字長さより小さかったら
for i := l downto j + 1 do // 文字の後ろから
result := s[i] + result; // 'e'迄コピー
end;
K := 1; // k=1初期化
for i := j downto 1 do begin // 'e'の前の文字から
c := s[i]; // 一文字取り出し'0'は読み飛ばす
if c <> ZC then begin // '0'で無かったら
k := i; // k=i
if c = DT then k := k + 1; // '.'だったら k=i+1 '.'の後の'0'は残す
break; // ブレーク
end;
end;
for i := k downto 1 do // kから1文字目までコピー
result := s[i] + result; // 前に追加コピー
end;
//---------------------------------- 誤差関数 ----------------------------------
// erf(z) 誤差関数
// z < 2.4 テーラー展開計算
// z >= 2.4 連分数計算
function Error_function(z : bigdecimal): bigdecimal;
const
IMAX = 350; // 連分数計算 Loop数
var
mzh2, zhn, s, tmp, y, a : bigdecimal;
epsilon, sabs : bigdecimal;
one, two, nl, nn : bigdecimal;
n : biginteger;
ione : biginteger;
dpcs, i : integer;
begin
dpcs := bigdecimal.DefaultPrecision; // 除算有効桁数
one := bigdecimal.One; // 1
ione := biginteger.One;
epsilon := EPSC; // 収束判定値
if z.Abs(z) < '2.4' then begin // テーラー展開
mzh2 := -z * z; // -z^2
s := z; // n = 0時 z
nl := one; // 0! = 1
zhn := z; // n = 0時 z
n := ione; // n=1から
repeat
nn := n + n + one; // 2n+1
nn := nn * nl; // n!(2n+1)
zhn := zhn * mzh2; // ((-1)^n)(z^(2n+1))
nn := nn.RoundToPrecision(dpcs); // 除算前桁合わせ
zhn := zhn.RoundToPrecision(dpcs); // 除算前桁合わせ
tmp := zhn / nn; // ((-1)^n)(z^(2n+1))/(n!(2n+1))
s := s + tmp; // Σ+Δ
n := n + ione; // inc(n)
nl := nl * n; // n!
sabs := tmp.Abs(tmp); // |Δ|
until sabs < epsilon;
result := s * pai2; // Σ* 2/√(π)
form1.nedit.Text := 'loops= ' + n.ToString;
exit;
end;
two := bigdecimal.two; // 連分数計算
y := z.Abs(z) * two; // 2z
n := IMAX;
a := bigdecimal.Zero; // a = 0
for i := IMAX downto 1 do begin
a := n * (two / (y + a));
n := n - ione;
end;
a := 1 - exp_big(-z * z) / (y + a) * two / pib.Sqrt(pib);
if z < '0' then result := -a
else result := a;
form1.nedit.Text := '連分数 loops= ' + inttostr(IMAX);
end;
//------------------------------------------------------------------------------
// 答0.99・9xxxの9の値を数えると同時に元の値から0.99・9xxx-0.99・9で0.00・xxxを得ます。
// 戻り値'9'の数
function nineNo(x : bigdecimal; var ans: bigdecimal): integer;
const
NINE = '9';
var
char9 : char;
i, lng, count : integer;
str, ninestr : string;
s9f : boolean;
nines : bigdecimal;
begin
s9f := false; // '9'フラグリセット
char9 := NINE; // '9'
str := x.ToPlainString; // x -> string
lng := length(str); // 文字長さ
ninestr := '0.'; // '0.'
count := 0; // '9'の数リセット
for i := 1 to lng do begin // 1文字目から
if str[i] = char9 then begin // '9'なら
if i = 3 then s9f := true; // 3文字目が'9'だったら'9'フラグセット
if s9f then begin // '9'フラグtrueなら
inc(count); // '9'の数インクリメント
ninestr := ninestr + char9; // '0.xx' + '9'
end;
end
else s9f := false; // '9'でなかったら'9'フラグリセット
end;
if count > 0 then begin // '9'の数が0以上なら
nines := ninestr; // '0.9・・9' -> 数値変換
ans := x - nines; // ans = 0.9・・9xxxxx - 0.9・・9 = 0.0・・0xxxxx
end
else ans := x; // ans = x 変化なし この時 '9'の数=0
result := count; // '9'の数
end;
//------------------------------------------------------------------------------
// error function calc
// zの値が∞だとerror関数の値が1になるのですが、演算桁数の関係で
// 50桁表示でzの値が10.7程度で1になってしまうため9の数での表現を採用しています。
Procedure calc_error_function;
var
z, absz, ans, mans, ansm99, zmax, one, ansmone : bigdecimal;
nineN : integer;
str99 : string;
begin
zmax := ZINMAX;
try
z := form1.zEdit.Text;
except
on EConverterror do begin
MessageDlg('z の値に間違いがあります。', mtError, [mbOK], 0);
exit;
end;
end;
absz := z.Abs(z);
if absz > zmax then begin
MessageDlg('z の絶対値が演算の最大値より大きくなっています。', mtError, [mbOK], 0);
exit;
end;
one := bigdecimal.One;
// error 関数計算
ans := Error_function(z);
// errorC 関数計算
mans := bigdecimal.One - ans;
// zの値が1.2を超えると0.999・・9の9の値が増えるの9の値を数で表現 0. + 9の数＋0.99・9を減算した値として表示
if z >= 0 then nineN := nineNo(ans, ansm99)
else nineN := nineNo(-ans, ansm99);
// 0.'9'・・・の'9'は有効桁数とならない様なので変更
ansm99 := ansm99.RoundToPrecision(50);
if ans = '0' then form1.ansREdit.Text := ' 0.0'
else begin
if (nineN > 0) and (Form1.CheckBox1.Checked = false) then begin
if ansm99 = bigdecimal.Zero then str99 := '0'
else str99 := ansm99.ToString;
if z >= 0 then Form1.ansREdit.Text := ' 0. 9xx' + inttostr(nineN) + '個 + ' + str99
else Form1.ansREdit.Text := '-0. 9xx' + inttostr(nineN) + '個 - ' + str99;
end
else begin
ans := ans.RoundToPrecision(50);
Form1.ansREdit.Text := ZeroErase(' ' + ans.ToString);
end;
end;
if mans > one then ansmone := mans - one
else ansmone := mans;
nineN := nineNo(ansmone, ansm99);
ansm99 := ansm99.RoundToPrecision(50);
if (nineN > 0) and (Form1.CheckBox1.Checked = false) then begin
if ansm99 = bigdecimal.Zero then str99 := '0'
else str99 := ansm99.ToString;
if mans > one then Form1.OneMansEdit.Text := ' 1. 9xx' + inttostr(nineN) + '個 + ' + str99
else Form1.OneMansEdit.Text := ' 0. 9xx' + inttostr(nineN) + '個 + ' + str99;
end
else begin
mans := mans.RoundToPrecision(50);
form1.OneMansEdit.Text := ' ' + ZeroErase(mans.ToString);
end;
end;
//----------------------------- 誤差関数計算 -----------------------------------
// erf(z)
procedure TForm1.calcBtnClick(Sender: TObject);
begin
calcBtn.Enabled:= false;
bigdecimal.DefaultPrecision := DPS;
calc_error_function;
calcBtn.Enabled:= true;
end;
//----------------------------- 逆誤差関数 -------------------------------------
// erfの計算からerfinvの値を逆算します
// erf(1)から始めてerf(x)の値をyに近づけます
function erfinv_function(y : bigdecimal; var n : integer): bigdecimal;
const
MINX1 = '1e-200';
// MINX2 = '1e-100'; // DPS = 1000
MINX2 = '1e-80'; // DPS = 600
var
ans, dx, mx, absy, ty, quarter : bigdecimal;
begin
if y = '0' then begin
result := '0';
exit;
end;
absy := y.Abs(y);
mx := MINX2;
if absy < '0.1' then mx := MINX1; // 値による収束判定値変更
quarter := bigdecimal.One / bigdecimal.Two;
quarter := quarter / bigdecimal.Two; // 0.25
dx := bigdecimal.Two; // 2
ty := dx;
n := 0;
repeat
ans := Error_function(ty); // 誤差関数
if ans > absy then begin
ty := ty - dx;
dx := dx * quarter; // dx * 0.25
ty := ty + dx;
end
else
ty := ty + dx;
inc(n);
until (dx < mx) or (ans = absy);
if y < '0' then ty := -ty;
result := ty;
end;
// 逆誤差関数の計算
procedure inverse_error_function(y : bigdecimal);
var
ans, absy, one, dlt : bigdecimal;
n : integer;
begin
if (y > '1') or (y < '-1') then begin
application.MessageBox('yの値が範囲外です。','注意', 0);
exit;
end;
absy := y.Abs(y);
if absy < '1' then begin
one := '1';
dlt := '1e-4346';
dlt := one - dlt;
if absy > dlt then begin // 0.9999999 9 9 が4345個迄
application.MessageBox('yの値が1に近すぎます。(0.9999・・・・9)','注意', 0);
exit;
end;
end;
if (y <> '0') and (absy < '1e-100') then begin
application.MessageBox('yの絶対値が小さすぎます。','注意', 0);
exit;
end;
if y = '1' then begin
Form1.memo1.Lines.Append('erfinv(1) = INFINITY');
exit;
end;
if y = '-1' then begin
Form1.memo1.Lines.Append('erfinv(-1) = -INFINITY');
exit;
end;
Form1.Memo1.Lines.Append('暫く時間が掛かります。');
application.ProcessMessages;
ans := erfinv_function(y, n); // 逆誤差関数
ans := ans.RoundToPrecision(50);
form1.Memo1.Clear;
Form1.memo1.Lines.Append('入力値 y = ' + y.ToPlainString);
Form1.memo1.Lines.Append('erfinv');
Form1.Memo1.Lines.Append('Loops = ' + intTostr(n));
if ans = '0' then
Form1.memo1.Lines.Append('erfinv(y) = 0.0')
else
Form1.memo1.Lines.Append('erfinv(y) = ' + ZeroErase(ans.ToString));
end;
// 逆誤差関数計算 y値入力
procedure TForm1.invBtnClick(Sender: TObject);
var
y : bigdecimal;
begin
try
y := form1.yEdit.Text;
except
on EConverterror do begin
MessageDlg('y の値に間違いがあります。', mtError, [mbOK], 0);
exit;
end;
end;
invBtn.Enabled := false;
memo1.Clear;
inverse_error_function(y); // 逆誤差関数
invBtn.Enabled := true;
end;
//------------------------------------------------------------------------------
// 0 そのまま文字9の後に文字として追加
// 1 0.99・・の値に x.xxe^-yとして加算
// 3 入力エラー
function p9aCondition(s : string; n9: integer): integer;
const
dc = '.';
me = 'e';
le = 'E';
mc = '-';
var
i, l : integer;
s9 : string;
b9, pa : bigdecimal;
cc : char;
EF : boolean;
begin
l := length(s); //文字の長さ
EF := false;
for i := l downto 1 do begin
cc := s[i];
if cc = me then EF := True;
if cc = le then EF := True;
if cc = dc then EF := True;
end;
if EF then begin
s9 := '1.0e-' + intTostr(n9);
b9 := s9;
pa := s;
if pa > s9 then begin
MessageDlg(' +α の値が大きすぎます。', mtWarning, [mbOK], 0);
result := 3;
exit;
end;
result := 1;
exit;
end;
result := 0;
end;
// 逆誤差関数計算
// 9の数入力モード
procedure TForm1.inv9BtnClick(Sender: TObject);
const
YMAX = 4345;
var
n9, ch, j : integer;
b9, pa, yb : bigdecimal;
ystr : string;
begin
val(n9edit.Text, n9, ch);
if ch <> 0 then begin
MessageDlg(' 9 のn数に間違いがあります。', mterror, [mbOK], 0);
exit;
end;
if n9 > YMAX then begin
MessageDlg(' 9 のn数は'+ intTostr(YMAX) + '迄です。', mtWarning, [mbOK], 0);
exit;
end;
try
pa := p9aEdit.Text;
except
on EConverterror do begin
MessageDlg('+α の値に間違いがあります。', mtError, [mbOK], 0);
exit;
end;
end;
ch := p9aCondition(p9aEdit.Text, n9);
if ch = 3 then exit; // 入力エラーなら終了
if ch = 0 then begin // テキスト加算
ystr := '0.';
for j := 1 to n9 do ystr := ystr + '9';
ystr := ystr + p9aEdit.Text;
try
yb := ystr;
except
on EConverterror do begin
MessageDlg('+α の値に間違いがあります。', mtError, [mbOK], 0);
exit;
end;
end;
end;
if ch = 1 then begin // 数値加算
ystr := '0.';
for j := 1 to n9 do ystr := ystr + '9';
b9 := ystr;
yb := b9 + pa;
end;
memo1.Clear;
memo1.Lines.Append('入力値 y = ' + yb.ToPlainString);
memo1.Lines.Append('約 ' + floattostr(inversetime(n9)) + '秒位');
inv9Btn.Enabled := false;
inverse_error_function(yb); // 逆誤差関数
inv9Btn.Enabled := true;
end;
//------------------------------------------------------------------------------
// 初期値
procedure TForm1.FormCreate(Sender: TObject);
var
two : bigdecimal;
begin
bigdecimal.DefaultPrecision := DPS; // 除算有効桁数設定
zedit.EditLabel.Caption := '|z|<=' + ZINMAX;
label1.Caption := 'Zの値が無限大の時erf(∞)=1となるのですが演算上入力の最大値は' + ZINMAX + 'です。';
nEdit.Text := 'loops =';
pib := pi_big; // π 600桁
two := bigdecimal.Two; // 2
pai2 := two / pib.Sqrt(pib, DPS + DPS); // 2/√(π)
end;
end.
Sub_big.pas
unit Sub_big; interface uses Vcl.Forms, Velthuis.BigIntegers, Velthuis.Bigdecimals; const DPS = 600; // 除算有効桁数 // 有効桁数が不足、収束判定値が大きいと演算結果が // 1.0を超えます。 var pib, pai2 : bigdecimal; // π bigdecimal function exp_big(x: bigdecimal): bigdecimal; // e~x function pi_big: Bigdecimal; // π implementation // exp(x) e^x 冪級数 テイラー級数 // exp(x) = 1 + x + x^2/2! + x^3/3! + x^4/4! .... function exp_big(x: bigdecimal): bigdecimal; var dpcs : integer; a, e, prev, zero, one, two, d : bigdecimal; i, ione: bigInteger; begin dpcs := BigDecimal.DefaultPrecision; zero := '0'; one := '1'; two := '2'; e := x; // exp(t)計算開始 e=x if x < zero then e := -x; // x が負数だったらe 正数に d := e; // d 初期値 e = /x/ a := d; // a 初期値 d = e = /x/ i := '2'; ione := '1'; repeat prev := e; // 判定値保存 a := a * (d / i); // a = (d^i)/(i!) a := a.RoundToPrecision(dpcs); e := e + a; // e = e + (d^i)/(i!) e := e.RoundToPrecision(dpcs); i := i + ione; // inc(i) until e = prev; // 桁落ちにより値が変わらなくなったら終了 e := e + one; // e = 1 + d + d^2/2! + d^3/3! ～ e := e.RoundToPrecision(dpcs); one := one.RoundToPrecision(dpcs); if x < '0' then e := one / e; // xが負数だったら答えは逆数 result := e; end; //--------------------------------- Ln(x)--------------------------------------- // x = m * 2^n のnの値と2^nの値を戻します // result = n // ta = 2^n // m = x / 2^n function frexpa(x: bigdecimal; var ta: biginteger): integer; var tb: biginteger; xi, one: bigdecimal; n, j, s, pcs : integer; begin pcs := BigDecimal.DefaultPrecision; one := '1'; one := one.RoundToPrecision(pcs); xi := x; // x保存 if xi < one then x := one / x; // 1より小さかったら逆数 ta := '1'; n := 0; j := 0; // シフト回数クリア ta := '1'; // ta初期値 s := 4096; // s=4^i i = 6 repeat while x > ta do begin biginteger.ShiftLeft(ta, s, tb); // s分左シフト ta := tb; inc(j); // シフト回数インクリメント end; if (s > 1) and (j > 0) then begin // ta > x になったら dec(j); // シフト回数デクリメント biginteger.Shiftright(ta, s, tb); // s分右シフト ta := tb; end; n := n + s * j; // 2^nのn計算 j := 0; // シフト回数クリア s := s shr 2; // sの値を1/4にする 右へ2ビットシフト // s := s div 4; // sの値を1/4にする until s = 0; // s= ...16, 4, 1, 0 if xi < one then begin // より小さかったら n := -n + 1; // 2^nのn値負数 biginteger.Shiftright(ta, 1, tb); // 上式+1により右シフト ta := tb; end; result := n // ta = 2^n end; // 小さい値のlog計算 // xi 実数 // dpcs 有効桁数 // ans log値 // 戻り値 Loopオーバーフロー 無し true 有り false // loop制限の無い場合 1e-4～1e4 が計算出来る範囲 // loop制限 5.8e-3 ～1.73e2 (kk=10000の場合) function Log_11(x: bigdecimal; dpcs: integer; var ans: bigdecimal): boolean; const KK = 10000; var one, two, x1, x2, i, s, last: bigdecimal; k : integer; begin result := true; one := '1'; two := '2'; x1 := (x - one) / (x + one); // x1 = (x-1)/(x+1) x2 := x1 * x1; // x1^2 x2 := x2.RoundToPrecision(dpcs); i := one; // i=1 s := x1; // s初期値 k := 0; // 長ループ脱出用カウンタ0 repeat x1 := x1 * x2; // x1^2n+1 x1 := x1.RoundToPrecision(dpcs); i := i + two; // 2n+1 i := i.RoundToPrecision(dpcs); last := s; // 判定用sの値保存 s := s + x1 / i; // Σs = s + x1^2n+1 / (2n+1) s := s.RoundToPrecision(dpcs); // 収束判定の為指定有効桁数以下丸め inc(k); // ループカウンタインクリメント until (last = s) or (k > KK); // 収束判定 ans := two * s; if k > kk then result := false; end; // loge(x) ln(x) // 級数展開 // 1e±500000 程度が限度 // sm <xi< last の範囲外の場合 (0.7～xi～1.4) * 2^nに変換 xiが1に近いほど変換早い function log_big(xi: bigdecimal): bigdecimal; const KK = 10000; var LOG2, SQRT2, two, last, s, sm, one, one1, k2, a: bigdecimal; k : integer; kb, ta : biginteger; dpcs : integer; begin result := '0'; if xi <= result then begin application.MessageBox('無効な値です。','注意',0); exit; end; sm := '1e-2'; last := '5e1'; dpcs := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ one := '1'; if xi = one then begin exit; end; if (xi > sm) and (xi < last) then begin // 0.01 < xi < 50の時はLog11計算 if Log_11(xi, dpcs, a) then begin // log11 result := a; exit; end; end; one1 := '1e500000'; if xi < one then begin // xi < 1 last := one / xi; // 1 / xi if last > one1 then begin // (1 / xi) > 1e500000 application.MessageBox('値が小さすぎます。','注意',0); exit; end; end; if xi > one1 then begin // xi > 1e500000 application.MessageBox('値が大きすぎます。','注意',0); exit; end; xi := xi.RoundToPrecision(dpcs); two := '2'; Log_11(two, dpcs, LOG2); // log(2) SQRT2 := bigdecimal.Sqrt(two, dpcs + dpcs); // √2 k := frexpa(xi / SQRT2, ta); // x / √2 = m * 2^k ta = 2^k kb := k; k2 := ta; // 2^k integer to decimal k2 := k2.RoundToPrecision(dpcs); if k < 0 then begin // kが負数だったら xi := xi * k2; // x * 2^k x=0.707～1.414 √2 xi := xi.RoundToPrecision(dpcs); end else begin xi := xi / k2; // x / 2^k x=0.707～1.414 √2 end; if xi <> one then begin // xi <> 1 なら Log_11(xi, dpcs, s) // log(xi) end else s := '0'; // xi=1なら s=0 result := LOG2 * kb + s; result := result.RoundToPrecision(dpcs); end; //------------------------------------------------------------------------------ // π // https://www.kurims.kyoto-u.ac.jp/~ooura/pi_fft-j.html // T.Ooura AGM アルゴリズ function pi_big: Bigdecimal; var n, dpcs : integer; SQRT_SQRT_EPSILON, c, b, e : BigDecimal; npow : Bigdecimal; a, one, two, four, five, eight : Bigdecimal; begin dpcs := BigDecimal.DefaultPrecision; // 指定精度 + α one := '1'; one := one.RoundToPrecision(dpcs); // oneの有効桁数をdpcsに設定 two := '2'; four := '4'; five := '5'; eight := '8'; SQRT_SQRT_EPSILON := one / BigDecimal.IntPower(two, dpcs shl 1); // 収束判定値 c := BigDecimal.Sqrt(one / eight, dpcs + dpcs); a := one + c + c + c; b := BigDecimal.Sqrt(a, dpcs + dpcs); e := b - five / eight; b := b + b; c := e - c; a := a + e; npow := '4'; n := 0; while (e > SQRT_SQRT_EPSILON) and (n < 100) do begin npow := npow + npow; // 8,16,32,64 e := (a + b) / two; // 平均値 除算有効桁数での丸め b := a * b; b := b.RoundToPrecision(dpcs); // pcs + α 丸め b := BigDecimal.Sqrt(b, dpcs + dpcs); // 平方根有効桁数での丸め e := e - b; b := b + b; c := c - e; a := e + b; inc(n); end; e := e * e; e := e.RoundToPrecision(dpcs); // pcs + α 丸め e := e / four; // e = e * e / 4 a := a + b; result := (a * a - e - e / two) / (a * c - e) / npow; // 除算の順番に注意 result := result.RoundToPrecision(dpcs); // 指定の精度に丸め end; end.
error_or_erfinv_Continued fraction.zip
三角関数、逆三角関数、その他関数 に戻る