逆誤差関数、誤差関数

　逆誤差関数(erfinv)、java script から変換したものが判りづらいのと、c++より変換したものより精度が良さそうなので、演算に配列を使用した、extended(long double)と多倍長のプログラムを作成してみました。
多倍長演算では、元データーが18桁程度なので、Doubleに併せて18桁表示としています、演算精度は、18:桁を維持します。
Doubleの演算では、0.99・・の場合、直ぐに1になってしまい、1直近では3桁程度しか精度が出ません。

　誤差関数(erf)のextended、doubleでの計算時、計算結果が1に近づくと、精度が悪くなるので、これの対策も検討しました。
誤差関数をテーラー展開した計算のみで行うと、収束判定を、値が変化しなくなった時点で収束したと判定するのですが、この方法だと、有効桁数より小さい値なのだが本来、加算されるべき値が加算されず桁落ちすることになります。
特に、erf(z)の値が1に近づくと顕著になります。
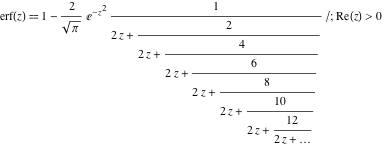
対策として、1に近づくような値の場合は、連分数を使用して計算するようにします。
多倍長演算を使用して、表示桁数に対して、数桁以上演算桁数を多くすれば桁落ちの心配はありませんが、演算数が増えます。

連分数

　連分数の計算は、１から減算する値を計算するので、桁落ちの様な問題は発生しません。
但し、連分数のでの計算は、zの値が小さくなると、連分数の深度が深くなり、計算数が増大します、そこで、zの値が小さい範囲では、テーラー展開の計算で行い、ある程度大きくなったら連分数の計算を行います。
此処での、プログラムは、2.4以下と、以上で切り分けています。
　テーラー展開の場合extended演算でerf(z)のzの値が最大で、4.7程度ですが、連分数を使うと6.1程度まで広がります。

プログラム

Biginteger & Bigdecimal の組み込み方は第１種ケルビン関数を参照して下さい。

Big_erfinvJs.pas

unit Big_erfinvJs;


interface

uses system.math, Vcl.Forms, Vcl.Dialogs, Velthuis.BigIntegers, Velthuis.Bigdecimals;

function erfinvjs_function_big(x : bigdecimal): bigdecimal;

implementation

uses main;

var
  p1 : array[0..1] of array[0..9] of bigdecimal;
  p2 : array[0..1] of array[0..9] of bigdecimal;
  p3 : array[0..3] of array[0..10] of bigdecimal;
  p4 : array[0..3] of array[0..8] of bigdecimal;
  p5 : array[0..3] of array[0..8] of bigdecimal;

  // Bigdecimal　に 直接設定出来ないので、一度文字配列にします。
  p1s: array[0..1] of array[0..9] of string =
    (('-0.0005087819496582806', '-0.008368748197417368', '0.03348066254097446', '-0.012692614766297404',
      '-0.03656379714117627', '0.02198786811111689', '0.008226878746769157', '-0.005387729650712429', '0.0', '0.0'),
     ('1.0', '-0.9700050433032906', '-1.5657455823417585', '1.5622155839842302', '0.662328840472003', '-0.7122890234154284',
      '-0.05273963823400997', '0.07952836873415717', '-0.0023339375937419', '0.0008862163904564247'));
  p2s: array[0..1] of array[0..8] of string =
    (('-0.20243350835593876', '0.10526468069939171', '8.3705032834312', '17.644729840837403', '-18.851064805871424',
      '-44.6382324441787', '17.445385985570866', '21.12946554483405', '-3.6719225470772936'),
     ('1.0', '6.242641248542475', '3.971343795334387', '-28.66081804998', '-20.14326346804852',
     '48.560921310873994', '10.826866735546016', '-22.643693341313973', '1.7211476576120028'));
  p3s: array[0..3] of array[0..10] of string =
    (('-0.1311027816799519', '-0.16379404719331705', '0.11703015634199525', '0.38707973897260434', '0.3377855389120359', '0.14286953440815717',
      '0.029015791000532906', '0.0021455899538880526','-6.794655751811263e-7', '2.8522533178221704e-8','-6.81149956853777e-10'),
     ('1.0', '3.4662540724256723', '5.381683457070069', '4.778465929458438', '2.5930192162362027', '0.848854343457902',
      '0.15226433829533179', '0.011059242293464892', '0.0', '0.0', '0.0'),
     ('-6.81149956853777e-10', '2.8522533178221704e-8', '-6.794655751811263e-7', '0.0021455899538880526', '0.029015791000532906', '0.14286953440815717',
      '0.3377855389120359', '0.38707973897260434', '0.11703015634199525', '-0.16379404719331705', '-0.1311027816799519'),
     ('0.0', '0.0', '0.0', '0.011059242293464892', '0.15226433829533179', '0.848854343457902',
      '2.5930192162362027', '4.778465929458438', '5.381683457070069', '3.4662540724256723', '1.0'));
  p4s: array[0..3] of array[0..8] of string =
    (('-0.0350353787183178', '-0.0022242652921344794', '0.018557330651423107', '0.009508047013259196', '0.0018712349281955923',
      '0.00015754461742496055', '0.00000460469890584318', '-2.304047769118826e-10', '2.6633922742578204e-12'),
     ('1.0', '1.3653349817554064', '0.7620591645536234', '0.22009110576413124', '0.03415891436709477',
      '0.00263861676657016', '0.00007646752923027944', '0.0', '0.0'),
     ('2.6633922742578204e-12', '-2.304047769118826e-10', '0.00000460469890584318', '0.00015754461742496055', '0.0018712349281955923',
      '0.009508047013259196', '0.018557330651423107', '-0.0022242652921344794', '-0.0350353787183178'),
     ('0.0', '0.0', '0.00007646752923027944', '0.00263861676657016', '0.03415891436709477',
      '0.22009110576413124', '0.7620591645536234', '1.3653349817554064', '1.0'));
  p5s: array[0..3] of array[0..8] of string =
    (('-0.016743100507663373', '-0.0011295143874558028', '0.001056288621524929', '0.00020938631748758808', '0.000014962478375834237',
      '4.4969678992770644e-7', '4.625961635228786e-9', '-2.811287356288318e-14', '9.905570997331033e-17'),
     ('1.0', '0.5914293448864175', '0.1381518657490833', '0.016074608709367652', '0.0009640118070051656',
      '0.000027533547476472603', '2.82243172016108e-7', '0.0', '0.0'),
     ('9.905570997331033e-17', '-2.811287356288318e-14', '4.625961635228786e-9', '4.4969678992770644e-7', '0.000014962478375834237',
      '0.00020938631748758808', '0.001056288621524929', '-0.0011295143874558028', '-0.016743100507663373'),
     ('0.0', '0.0', '2.82243172016108e-7', '0.000027533547476472603', '0.0009640118070051656',
      '0.016074608709367652', '0.1381518657490833', '0.5914293448864175', '1.0'));

//--------------------------------- Ln(x)---------------------------------------
// x = m * 2^n のnの値と2^nの値を戻します
// result = n
// ta     = 2^n
// m = x / 2^n
function frexpa(x: bigdecimal; var ta: biginteger): integer;
var
  tb: biginteger;
  xi, one: bigdecimal;
  n, j, s, pcs : integer;
begin
  pcs := BigDecimal.DefaultPrecision;
  one := '1';
  one := one.RoundToPrecision(pcs);
  xi := x;                          // x保存
  if xi < one then x := one / x;    // 1より小さかったら逆数
  ta := '1';
  n := 0;
  j := 0;                           // シフト回数クリア
  ta := '1';                        // ta初期値
  s := 4096;                        // s=4^i    i = 6
  repeat
    while x > ta do begin
      biginteger.ShiftLeft(ta, s, tb);  // s分左シフト
      ta := tb;
      inc(j);                           // シフト回数インクリメント
    end;
    if (s > 1) and (j > 0) then begin   // ta > x になったら
      dec(j);                           // シフト回数デクリメント
      biginteger.Shiftright(ta, s, tb); // s分右シフト
      ta := tb;
    end;
    n := n + s * j;                     // 2^nのn計算
    j := 0;                             // シフト回数クリア
    s := s shr 2;                       // sの値を1/4にする   右へ2ビットシフト
//    s := s div 4;                       // sの値を1/4にする
  until s = 0;            // s= ...16, 4, 1, 0
  if xi < one then begin                // より小さかったら
    n := -n + 1;                        // 2^nのn値負数
    biginteger.Shiftright(ta, 1, tb);   // 上式+1により右シフト
    ta := tb;
  end;
  result := n                             // ta = 2^n
end;

// 小さい値のlog計算
// xi 実数
// dpcs 有効桁数
// ans log値
// 戻り値 Loopオーバーフロー 無し true  有り false
// loop制限の無い場合 1e-4～1e4 が計算出来る範囲
// loop制限 5.8e-3 ～1.73e2  (kk=10000の場合)
function Log_11(x: bigdecimal; dpcs: integer; var ans: bigdecimal): boolean;
const
  KK = 10000;
var
  one, two, x1, x2, i, s, last: bigdecimal;
  k : integer;
begin
  result := true;
  one := '1';
  two := '2';
  x1 := (x - one) / (x + one);                      // x1 = (x-1)/(x+1)
  x2 := x1 * x1;                                    // x1^2
  x2 := x2.RoundToPrecision(dpcs);
  i := one;                                         // i=1
  s := x1;                                          // s初期値
  k := 0;                                           // 長ループ脱出用カウンタ0
  repeat
    x1 := x1 * x2;                                  // x1^2n+1
    x1 := x1.RoundToPrecision(dpcs);
    i := i + two;                                   // 2n+1
    i := i.RoundToPrecision(dpcs);
    last := s;                                      // 判定用sの値保存
    s := s + x1 / i;                                // Σs = s + x1^2n+1 / (2n+1)
    s := s.RoundToPrecision(dpcs);                  // 収束判定の為指定有効桁数以下丸め
    inc(k);                                         // ループカウンタインクリメント
  until (last = s) or (k > KK);                     // 収束判定
  ans := two * s;
  if k > kk then result := false;
end;

// loge(x)    ln(x)
// 級数展開
// 1e±500000 程度が限度
// sm <xi< last の範囲外の場合 (0.7～xi～1.4) * 2^nに変換 xiが1に近いほど変換早い
function log_big(xi: bigdecimal): bigdecimal;
const
  KK = 10000;
var
  LOG2, SQRT2, two, last, s, sm, one, one1, k2, a: bigdecimal;
  k, dpcs : integer;
  kb, ta : biginteger;
begin
  dpcs := bigdecimal.DefaultPrecision;
  result := '0';
  if xi <= result then begin
    application.MessageBox('無効な値です。','注意',0);
    exit;
  end;
  sm := '1e-2';
  last := '5e1';
  one := '1';
  if xi = one then begin
    exit;
  end;
  if (xi > sm) and (xi < last) then begin             // 0.01 < xi < 50の時はLog11計算
    if Log_11(xi, dpcs, a) then begin                 // log11
      result := a;
      exit;
    end;
  end;
  one1 := '1e500000';
  if xi < one then begin                              // xi < 1
    last := one / xi;                                 // 1 / xi
    if last > one1 then begin                         // (1 / xi) > 1e500000
      application.MessageBox('値が小さすぎます。','注意',0);
      exit;
    end;
  end;
  if xi > one1 then begin                             // xi > 1e500000
    application.MessageBox('値が大きすぎます。','注意',0);
    exit;
  end;
  xi := xi.RoundToPrecision(dpcs);
  two := '2';
  Log_11(two, dpcs, LOG2);                            // log(2)
  SQRT2 := bigdecimal.Sqrt(two, dpcs * 2);            // √2
  k := frexpa(xi / SQRT2, ta);                        // x / √2 = m * 2^k  ta = 2^k
  kb := k;
  k2 := ta;                                           // 2^k  integer to decimal
  k2 := k2.RoundToPrecision(dpcs);
  if k < 0 then begin                                 // kが負数だったら
    xi := xi * k2;                                    // x * 2^k   x=0.707～1.414  √2
    xi := xi.RoundToPrecision(dpcs);
  end
  else begin
    xi := xi / k2;                                    // x / 2^k   x=0.707～1.414  √2
  end;
  if xi <> one then begin                             // xi <> 1 なら
    Log_11(xi, dpcs, s)                               // log(xi)
  end
  else s := '0';                                      // xi=1なら s=0
  result := LOG2 * kb + s;
end;

// 文字配列からBigdecimal値に読み込みます
//  p1 : array [0..1] of array[0..9] of bigdecimal;
//  p2 : array [0..1] of array[0..9] of bigdecimal;
//  p3 : array [0..3] of array[0..10] of bigdecimal;
//  p4 : array [0..3] of array[0..8] of bigdecimal;
//  p5 : array [0..3] of array[0..8] of bigdecimal;
procedure pnread;
var
  i, j : integer;
begin
  for i := 0 to 1 do
    for j := 0 to 9 do  p1[i, j] := p1s[i, j];
  for i := 0 to 1 do
    for j := 0 to 9 do  p2[i, j] := p2s[i, j];
  for i := 0 to 3 do
    for j := 0 to 10 do  p3[i, j] := p3s[i, j];
  for i := 0 to 3 do
    for j := 0 to 8 do  p4[i, j] := p4s[i, j];
  for i := 0 to 3 do
    for j := 0 to 8 do  p5[i, j] := p5s[i, j];
end;

function erfinvjs_function_big(x :  bigdecimal):  bigdecimal;
const
  Y1 = '8.91314744949340820313e-2';
  Y2 = '2.249481201171875';
  Y3 = '8.07220458984375e-1';
  Y4 = '9.3995571136474609375e-1';
  Y5 = '9.8362827301025390625e-1';
var
  sign, ax, qs, q, g, r, tmp : bigdecimal;
  dpcs : integer;

  function rational_p1q1(x : bigdecimal): bigdecimal;
  var
    s1, s2 : bigdecimal;
    i : integer;
  begin
　　if x = '0.0'  then begin
      result := '-0.0005087819496582806';
      exit;
    end;
    s1 := '0.0';
    for i := 9 downto 1 do s1 := x * (p1[0, i] + s1);
    s1 := s1 + p1[0, 0];
    s2 := '0.0';
    for I := 9 downto 1 do s2 := x * (p1[1, i] + s2);
    s2 := s2 + p1[1, 0];
    s1 := s1.RoundToPrecision(dpcs);
    s2 := s2.RoundToPrecision(dpcs);
    result := s1 / s2;
  end;

  function rational_p2q2(x : bigdecimal): bigdecimal;
  var
    s1, s2 : bigdecimal;
    i : integer;
  begin
    if x = '0.0' then begin
      result :=  '-0.20243350835593876';
      exit;
    end;
    s1 := '0.0';
    for i := 8 downto 1 do s1 := x * (p2[0, i] + s1);
    s1 := s1 + p2[0, 0];
    s2 := '0.0';
    for I := 8 downto 1 do s2 := x * (p2[1, i] + s2);
    s2 := s2 + p2[1, 0];
    s1 := s1.RoundToPrecision(dpcs);
    s2 := s2.RoundToPrecision(dpcs);
    result := s1 / s2;
  end;

  function rational_p3q3(x : bigdecimal): bigdecimal;
  var
    ax, ix, s1, s2 : bigdecimal;
    i : integer;
  begin
    if x = '0.0' then begin
      result := '-0.1311027816799519';
      exit;
    end;
    ax := x.Abs(x);
    if ax <= '1.0' then begin
      s1 := '0.0';
      for i := 10 downto 1 do s1 := x * (p3[0, i] + s1);
      s1 := s1 + p3[0, 0];
      s2 := '0.0';
      for I := 10 downto 1 do s2 := x * (p3[1, i] + s2);
      s2 := s2 + p3[1, 0];
    end
    else begin
      ix := '1.0' / x;
      s1 := '0.0';
      for i := 10 downto 1 do s1 := ix * (p3[2, i] + s1);
      s1 := s1 + p3[2, 0];
      s2 := '0.0';
      for I := 10 downto 1 do s2 := ix * (p3[3, i] + s2);
      s2 := s2 + p3[3, 0];
    end;
    s1 := s1.RoundToPrecision(dpcs);
    s2 := s2.RoundToPrecision(dpcs);
    result := s1 / s2;
  end;

  function rational_p4q4(x : bigdecimal): bigdecimal;
  var
    ax, ix, s1, s2 : bigdecimal;
    i : integer;
  begin
    if x = '0.0' then begin
      result := '-0.0350353787183178';
      exit;
    end;
    ax := x.Abs(x);
    if ax <= '1.0' then begin
      s1 := '0.0';
      for i := 8 downto 1 do s1 := x * (p4[0, i] + s1);
      s1 := s1 + p4[0, 0];
      s2 := '0.0';
      for I := 8 downto 1 do s2 := x * (p4[1, i] + s2);
      s2 := s2 + p4[1, 0];
    end
    else begin
      ix := '1.0' / x;
      s1 := '0.0';
      for i := 8 downto 1 do s1 := ix * (p4[2, i] + s1);
      s1 := s1 + p4[2, 0];
      s2 := '0.0';
      for I := 8 downto 1 do s2 := ix * (p4[3, i] + s2);
      s2 := s2 + p4[3, 0];
    end;
    s1 := s1.RoundToPrecision(dpcs);
    s2 := s2.RoundToPrecision(dpcs);
    result := s1 / s2;
  end;

  function rational_p5q5(x : bigdecimal): bigdecimal;
  var
    ax, ix, s1, s2 : bigdecimal;
    i : integer;
  begin
    if x = '0.0' then begin
      result := '-0.016743100507663373';
      exit;
    end;
    ax := x.Abs(x);
    if ax <= '1.0' then begin
      s1 := '0.0';
      for i := 8 downto 1 do s1 := x * (p5[0, i] + s1);
      s1 := s1 + p5[0, 0];
      s2 := '0.0';
      for I := 8 downto 1 do s2 := x * (p5[1, i] + s2);
      s2 := s2 + p5[1, 0];
    end
    // 精度10byte以上でないと使用されない
    else begin
      ix := '1.0' / x;
      s1 := '0.0';
      for i := 8 downto 1 do s1 := ix * (p5[2, i] + s1);
      s1 := s1 + p5[2, 0];
      s2 := '0.0';
      for I := 8 downto 1 do s2 := ix * (p5[3, i] + s2);
      s2 := s2 + p5[3, 0];
    end;
    s1 := s1.RoundToPrecision(dpcs);
    s2 := s2.RoundToPrecision(dpcs);
    result := s1 / s2;
  end;

begin
  if (x < '-1') or (x > '1') then begin
    result := '0.0';
    exit;
  end;
  if x = '0.0' then begin
    result :=  x;
    exit;
  end;
  if  x < '0.0' then sign := '-1.0'
                else sign := '1.0';
  ax := x.Abs(x);
  dpcs := bigdecimal.DefaultPrecision;
  // |x| <= 0.5
  if ax <= '0.5' then begin                   // 0<|x|<=0.5
    g := ax * (ax + '10.0');
    r := rational_p1q1(ax);                   // ax = 0～0.5
    result := sign * ((g * Y1) + (g * r));
    exit;
  end;
  q := '1.0' - ax;
  // 1-|x| >= 0.25
  if q >= '0.25' then begin                   // 0.5<|x|<=0.75
    g := g.Sqrt('-2.0' * log_big(q));
    q := q - '0.25';
    r := rational_p2q2(q);                    // q = 0～0.25
    tmp := Y2 + r;
    g := g.RoundToPrecision(dpcs);
    tmp := tmp.RoundToPrecision(dpcs);
    result := sign * (g / tmp);
    exit;
  end;
  // |x| > 0.75
  q := q.sqrt(-log_big(q), dpcs);
  // q < 3
  if q < '3.0' then begin                     // 0.75<|x|<0.999876
    qs := q - '1.125';
    r := rational_p3q3(qs);                   // qs =  0.05241～3
    result := sign * ((Y3 * q) + (r * q));
    exit;
  end;
  // 3 =< q < 6
  if q < '6.0' then begin                     // 0.999876<|x|<0.999999999999999768
    qs := q - '3.0';
    r := rational_p4q4(qs);                   // qs = 0～3
    result := sign * ((Y4 * q) + (r * q));
    exit;
  end;
  // 6 =< q < 18                              // 0.999999999999999768<|x|<1
  qs := q - '6.0';                            // qs = 0～10
  r := rational_p5q5(qs);
  result := sign * ((Y5* q) + (r * q));
end;

initialization
  pnread;                 // string -> bigdecimal

end.

erfinvJs.pas

unit erfinvJs;

interface

function erfinvjs_function(x : extended): extended;

implementation

uses system.math, main, system.SysUtils;

var
  p1: array[0..1] of array[0..9] of extended =
    ((-0.0005087819496582806, -0.008368748197417368, 0.03348066254097446, -0.012692614766297404,
      -0.03656379714117627, 0.02198786811111689, 0.008226878746769157, -0.005387729650712429, 0.0, 0.0),
     ( 1.0, -0.9700050433032906, -1.5657455823417585, 1.5622155839842302, 0.662328840472003, -0.7122890234154284,
      -0.05273963823400997, 0.07952836873415717, -0.0023339375937419, 0.0008862163904564247));
  p2: array[0..1] of array[0..8] of extended =
    ((-0.20243350835593876, 0.10526468069939171, 8.3705032834312, 17.644729840837403, -18.851064805871424,
      -44.6382324441787, 17.445385985570866, 21.12946554483405, -3.6719225470772936),
     ( 1.0, 6.242641248542475, 3.971343795334387, -28.66081804998, -20.14326346804852,
       48.560921310873994, 10.826866735546016, -22.643693341313973, 1.7211476576120028));
  p3: array[0..3] of array[0..10] of extended =
    (( -0.1311027816799519, -0.16379404719331705, 0.11703015634199525, 0.38707973897260434, 0.3377855389120359, 0.14286953440815717,
       0.029015791000532906, 0.0021455899538880526, -6.794655751811263e-7, 2.8522533178221704e-8,-6.81149956853777e-10),
     ( 1.0, 3.4662540724256723, 5.381683457070069, 4.778465929458438, 2.5930192162362027, 0.848854343457902,
       0.15226433829533179, 0.011059242293464892, 0.0, 0.0, 0.0),
     (-6.81149956853777e-10, 2.8522533178221704e-8, -6.794655751811263e-7, 0.0021455899538880526, 0.029015791000532906, 0.14286953440815717,
       0.3377855389120359, 0.38707973897260434, 0.11703015634199525, -0.16379404719331705, -0.1311027816799519),
     ( 0.0, 0.0, 0.0, 0.011059242293464892, 0.15226433829533179, 0.848854343457902,
       2.5930192162362027, 4.778465929458438, 5.381683457070069, 3.4662540724256723, 1.0));
  p4: array[0..3] of array[0..8] of extended =
    ((-0.0350353787183178, -0.0022242652921344794, 0.018557330651423107, 0.009508047013259196, 0.0018712349281955923,
       0.00015754461742496055, 0.00000460469890584318, -2.304047769118826e-10, 2.6633922742578204e-12),
     ( 1.0, 1.3653349817554064, 0.7620591645536234, 0.22009110576413124, 0.03415891436709477,
       0.00263861676657016, 0.00007646752923027944, 0.0, 0.0),
     ( 2.6633922742578204e-12, -2.304047769118826e-10, 0.00000460469890584318, 0.00015754461742496055, 0.0018712349281955923,
       0.009508047013259196, 0.018557330651423107, -0.0022242652921344794, -0.0350353787183178),
     ( 0.0, 0.0, 0.00007646752923027944, 0.00263861676657016, 0.03415891436709477,
       0.22009110576413124, 0.7620591645536234, 1.3653349817554064, 1.0));
  p5: array[0..3] of array[0..8] of extended =
    ((-0.016743100507663373, -0.0011295143874558028, 0.001056288621524929, 0.00020938631748758808, 0.000014962478375834237,
       4.4969678992770644e-7, 4.625961635228786e-9, -2.811287356288318e-14, 9.905570997331033e-17),
     ( 1.0, 0.5914293448864175, 0.1381518657490833, 0.016074608709367652, 0.0009640118070051656,
       0.000027533547476472603, 2.82243172016108e-7, 0.0, 0.0),
     ( 9.905570997331033e-17, -2.811287356288318e-14, 4.625961635228786e-9, 4.4969678992770644e-7, 0.000014962478375834237,
       0.00020938631748758808, 0.001056288621524929, -0.0011295143874558028, -0.016743100507663373),
     ( 0.0, 0.0, 2.82243172016108e-7, 0.000027533547476472603, 0.0009640118070051656,
       0.016074608709367652, 0.1381518657490833, 0.5914293448864175, 1.0));

function erfinvjs_function(x : extended): extended;
const
  Y1 = 8.91314744949340820313e-2;
  Y2 = 2.249481201171875;
  Y3 = 8.07220458984375e-1;
  Y4 = 9.3995571136474609375e-1;
  Y5 = 9.8362827301025390625e-1;
var
  sign, ax, qs, q, g, r : extended;

  function rational_p1q1(x : extended): extended;
  var
    s1, s2 : extended;
    i : integer;
  begin
    if x = 0.0  then begin
      result := -0.0005087819496582806;
      exit;
    end;
    s1 := 0;
    for i := 9 downto 1 do s1 := x * (p1[0, i] + s1);
    s1 := s1 + p1[0, 0];
    s2 := 0;
    for I := 9 downto 1 do s2 := x * (p1[1, i] + s2);
    s2 := s2 + p1[1, 0];
    result := s1 / s2;
  end;

  function rational_p2q2(x : extended): extended;
  var
    s1, s2 : extended;
    i : integer;
  begin
    if x = 0.0 then begin
      result :=  -0.20243350835593876;
      exit;
    end;
    s1 := 0;
    for i := 8 downto 1 do s1 := x * (p2[0, i] + s1);
    s1 := s1 + p2[0, 0];
    s2 := 0;
    for I := 8 downto 1 do s2 := x * (p2[1, i] + s2);
    s2 := s2 + p2[1, 0];
    result := s1 / s2;
  end;

  function rational_p3q3(x : extended): extended;
  var
    ax, ix, s1, s2 : extended;
    i : integer;
  begin
    if x = 0.0 then begin
      result := -0.1311027816799519;
      exit;
    end;
    ax := abs(x);
    if ax <= 1.0 then begin
      s1 := 0;
      for i := 10 downto 1 do s1 := x * (p3[0, i] + s1);
      s1 := s1 + p3[0, 0];
      s2 := 0;
      for I := 10 downto 1 do s2 := x * (p3[1, i] + s2);
      s2 := s2 + p3[1, 0];
    end
    else begin
      ix := 1.0 / x;
      s1 := 0;
      for i := 10 downto 1 do s1 := ix * (p3[2, i] + s1);
      s1 := s1 + p3[2, 0];
      s2 := 0;
      for I := 10 downto 1 do s2 := ix * (p3[3, i] + s2);
      s2 := s2 + p3[3, 0];
    end;
    result := s1 / s2;
  end;

  function rational_p4q4(x : extended): extended;
  var
    ax, ix, s1, s2 : extended;
    i : integer;
  begin
    if x = 0.0 then begin
      result := -0.0350353787183178;
      exit;
    end;
    ax := abs(x);
    if ax <= 1.0 then begin
      s1 := 0;
      for i := 8 downto 1 do s1 := x * (p4[0, i] + s1);
      s1 := s1 + p4[0, 0];
      s2 := 0;
      for I := 8 downto 1 do s2 := x * (p4[1, i] + s2);
      s2 := s2 + p4[1, 0];
    end
    else begin
      ix := 1.0 / x;
      s1 := 0;
      for i := 8 downto 1 do s1 := ix * (p4[2, i] + s1);
      s1 := s1 + p4[2, 0];
      s2 := 0;
      for I := 8 downto 1 do s2 := ix * (p4[3, i] + s2);
      s2 := s2 + p4[3, 0];
    end;
    result := s1 / s2;
  end;

  function rational_p5q5(x : extended): extended;
  var
    ax, ix, s1, s2 : extended;
    i : integer;
  begin
    if x = 0.0 then begin
      result := -0.016743100507663373;
      exit;
    end;
    ax := abs(x);
    if ax <= 1.0 then begin
      s1 := 0;
      for i := 8 downto 1 do s1 := x * (p5[0, i] + s1);
      s1 := s1 + p5[0, 0];
      s2 := 0;
      for I := 8 downto 1 do s2 := x * (p5[1, i] + s2);
      s2 := s2 + p5[1, 0];
    end
    // 精度10byte以上でないと使用されない
    else begin
      ix := 1.0 / x;
      s1 := 0;
      for i := 8 downto 1 do s1 := ix * (p5[2, i] + s1);
      s1 := s1 + p5[2, 0];
      s2 := 0;
      for I := 8 downto 1 do s2 := ix * (p5[3, i] + s2);
      s2 := s2 + p5[3, 0];
    end;
    result := s1 / s2;
  end;

begin
  if (x < -1) or (x > 1) then begin
    result := 0;
    exit;
  end;
  if x = 1.0 then begin
    result := infinity;
    exit;
  end;
  if x = -1.0 then begin
    result := - infinity;
    exit;
  end;
  if x = 0.0 then begin
    result := x;
    exit;
  end;
  if  x < 0.0 then sign := -1.0
              else sign := 1.0;
  ax := abs(x);
  // |x| <= 0.5
  if ax <= 0.5 then begin                   // 0<|x|<=0.5
    g := ax * (ax + 10.0);
    r := rational_p1q1(ax);                 // ax = 0～0.5
    result := sign * ((g * Y1) + (g * r));
    exit;
  end;
  q := 1.0 - ax;
  // 1-|x| >= 0.25
  if q >= 0.25 then begin                   // 0.5<|x|<=0.75
    g := sqrt(-2.0 * ln(q));
    q := q - 0.25;
    r := rational_p2q2(q);                  // q = 0～0.25
    result := sign * (g / (Y2 + r));
    exit;
  end;
  // |x| > 0.75
  q := sqrt(-ln(q));
  // q < 3
  if q < 3.0 then begin                     // 0.75<|x|<0.999876
    qs := q - 1.125;
    r := rational_p3q3(qs);                 // qs =  0.05241～3
    result := sign * ((Y3 * q) + (r * q));
    exit;
  end;
  // 3 =< q < 6
  if q < 6.0 then begin                     // 0.999876<|x|<0.999999999999999768
    qs := q - 3.0;
    r := rational_p4q4(qs);                 // qs = 0～3
    result := sign * ((Y4 * q) + (r * q));
    exit;
  end;
  // 6 =< q < 18                            // 0.999999999999999768<|x|<1
  qs := q - 6.0;                            // qs = 0～10
  r := rational_p5q5(qs);
  result := sign * ((Y5* q) + (r * q));
end;

end.

erf.pas

unit erf;

interface

function erf_function(x : extended): extended;

implementation

uses system.math;

// 誤差関数
// テーラー展開と連分数
function erf_function(x : extended): extended;
var
  n: integer;
  absx: extended;
  a, c, y, ab : extended;
begin
  absx := abs(x);
  if absx < 2.4 then begin                          // テーラー展開
    c := 1;
    a := 0;
    n := 1;
    repeat
      ab := a;
      a := a + x / (2 * n - 1) * c;
      c := -c * x * x / n;
      inc(n);
    until ab = a;
    result :=  a * 2 / sqrt(pi);
    exit;
  end;
  y := absx * 2;                                    // 連分数
  a := 0;
  for n := 40 downto 1 do a := n * 2 / (y + a);
  a := 1 - exp(-x * x) / (y + a) * 2 / sqrt(pi);
  if x < 0 then result := -a
           else result := a;
end;

end.

main.pas

unit main;

interface

uses
  Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
  Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls;

type
  TForm1 = class(TForm)
    Memo1: TMemo;
    erfinvBtn: TButton;
    yEdit: TLabeledEdit;
    zEdit: TLabeledEdit;
    erfBtn: TButton;
    procedure erfinvBtnClick(Sender: TObject);
    procedure erfBtnClick(Sender: TObject);
  private
    { Private 宣言 }
  public
    { Public 宣言 }
  end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

uses system.math, system.UITypes, erfinvJs, erf, Big_erfinvJs, Velthuis.BigIntegers, Velthuis.Bigdecimals;

procedure TForm1.erfBtnClick(Sender: TObject);
var
  z, ans : extended;
  i : integer;
  {$IFDEF CPUX86}                                 // プラットフォーム32ビット
    L : integer;
  {$ENDIF CPUX86}
begin
  val(zedit.Text, z, i);
  if i <> 0 then begin
    application.MessageBox('yの値に間違いがあります。','注意',0);
    exit;
  end;
  memo1.Clear;
  {$IFDEF CPUX86}                                 // プラットフォーム32ビット
    L := length(zedit.Text);
    if L > 30 then z := strtofloat(Formatfloat('#0.########################', z));  // 0.9999999999999999 =>'1'-> 1
    memo1.Lines.Append('x86 mode');
  {$ENDIF CPUX86}
  {$IFDEF CPUX64}                                 // プラットフォーム32ビット
    z := strTofloat(floattostr(z));
    memo1.Lines.Append('x64 mode');
  {$ENDIF CPUX64}
  ans := erf_function(z);
  {$IFDEF CPUX86}                                 // プラットフォーム32ビット
    memo1.Lines.Append('Extended 演算');
  {$ENDIF CPUX86}
  {$IFDEF CPUX64}                                 // プラットフォーム32ビット
    memo1.Lines.Append('double 演算');
  {$ENDIF CPUX64}
  memo1.Lines.Append(' erf= ' + Formatfloat('#0.########################', ans));
end;

procedure TForm1.erfinvBtnClick(Sender: TObject);
var
  x, ans: extended;
  xb, ansb : bigdecimal;
  i : integer;
  {$IFDEF CPUX86}                                 // プラットフォーム32ビット
    L : integer;
  {$ENDIF CPUX86}
begin
  val(yedit.Text, x, i);
  if i <> 0 then begin
    application.MessageBox('yの値に間違いがあります。','注意',0);
    exit;
  end;

  try
    xb := yedit.Text;
  except
    on EConverterror do begin
      MessageDlg('x の値に間違いがあります。', mtError, [mbOK], 0);
      exit;
    end;
  end;
  memo1.Clear;
  {$IFDEF CPUX86}                                 // プラットフォーム32ビット
    L := length(yedit.Text);
    if L > 30 then x := strtofloat(Formatfloat('#0.########################', x));  // 0.9999999999999999 =>'1'-> 1
    memo1.Lines.Append('x86 mode');
  {$ENDIF CPUX86}
  {$IFDEF CPUX64}                                 // プラットフォーム32ビット
    x := strTofloat(floattostr(x));
    memo1.Lines.Append('x64 mode');
  {$ENDIF CPUX64}

  memo1.Lines.Append('inverse error function');
  ans := erfinvjs_function(x);
  {$IFDEF CPUX86}                                 // プラットフォーム32ビット
    memo1.Lines.Append('Extended js 演算');
  {$ENDIF CPUX86}
  {$IFDEF CPUX64}                                 // プラットフォーム32ビット
    memo1.Lines.Append('double js 演算');
  {$ENDIF CPUX64}
//  memo1.Lines.Append(' erfinv= ' + floattostr(ans));
  memo1.Lines.Append(' erfinv= ' + Formatfloat('#0.########################', ans));

  memo1.Lines.Append('');

  memo1.Lines.Append('多倍長演算 js 18桁表示');
  if (xb = '1.0') or (xb = '-1.0') then begin
    if xb >= '0.0' then memo1.Lines.Append(' erfinv=  INFINITY')
                   else memo1.Lines.Append(' erfinv= -INFINITY')
  end
  else begin
    ansb := erfinvjs_function_big(xb);
    ansb := ansb.RoundToPrecision(18);
    if ansb = '0.0' then
      memo1.Lines.Append(' erfinv= 0.0')
    else
      memo1.Lines.Append(' erfinv= ' + ansb.ToString);
  end;
end;

end.

erfinv_function_Js.zip

　　三角関数、逆三角関数、その他関数　に戻る