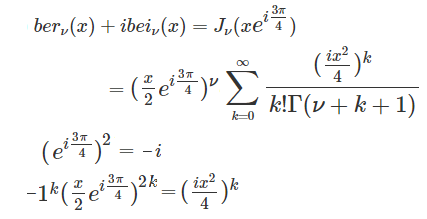
2024/03/26 計算ルーチンを見直して演算を早くしました。
ｘの値を実数とする第１種ケルビン関数
第１種ケルビン関数
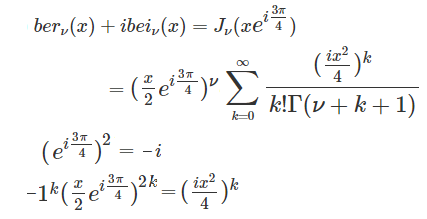
第１種ベッセル関数により計算が出来ますが、計算を簡単にする為上記の計算を使用します。
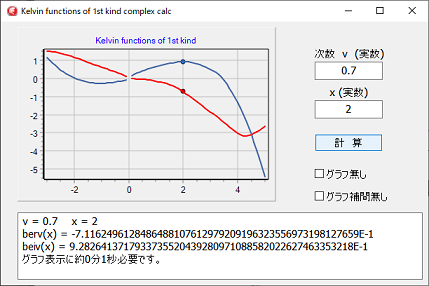次数ｖ変数ｘは両方とも実数で、答えは実数と虚数になります。
次数ｖの最大値は±100です。
グラフは、
赤が実数で青が虚数です。。。。。
グラフを作成するのに、全ての点を計算すると、非常に時間が掛かる為、十数点を計算し、ａｋｉｍａスプライン補間を使用して作図していますので、プロットされた点と、ラインが多少ずれる場合があります。
プログラム
複素数でケルビン関数の計算をする為には、Delphi標準のVariantによる複素数では、有効桁数が不足するので、多倍長演算を使用します。
ベッセル関数の計算を使用しているのでベッセル関数と同じです。
多倍長の組み込みは MPArithからmparith_2018-11-27.zipをダウンロードして下さい。
Zipファイルを解凍して、解凍したフォルダーにパス(ツール->オプション->Delphiオプション->ライブラリ->ライブラリパス)を追加し、Uses に mp_types, mp_real, mp_cmplx,
mp_baseを追加すれば使用可能になります。
また、今回はMPArithだけではなく、Rudy's Delphi CornerのBigintegerを使用します。
此処には、BigDecimalもあります。
特徴として、四則演算 + - * / 等がそのまま利用できることです。
但し、三角関数や対数関数はありません。
Rudy's Delphi Cornerを開いたら -> Free Coad -> Bigintegers for Delphi 又は BigDecimals for Delph -> 上の行の最後のリンク DelphiBigNumbers project on GitHub ->Coad▼-> Download ZIP でダウンロードします。
DelphiBigNumbers-master.zip がダウンロード出来たら、解凍したSorce フォルダーを、適当な場所にコピーして、そこへパス(ツール->オプション->Delphiオプション->ライブラリ->ライブラリパス)を追加し、usesに Velthuis.BigDecimals Velthuis.BigIntegers を追加すれば、BigDecimal Biginteger が使用可能となります。
使用方法は、解凍されたPDFファイルを参照してください。
Bigintegerは、ベルヌーイ数の計算にしようします、ベルヌーイ数はガンマ関数の計算に必要なのですが、固定値の配列として与えるのが大変なので、プログラム内で作成します。
Bigintegerと、mp_floatはデーター形式が違うので、テキスト形式で値の受け渡しをします。
Bigintegerは整数形式で、mp_floatの方が有効桁数が低い場合、mp_floatは、指数形式で、有効桁数に丸めて読み込むことが出来ます。
此処では、Bigintegerからmp_floatへの変換しか行いません。
* 重要
複素数の計算にべき乗があるのですが、Delphiに用意されている VerComplexPower、
Mp_complex に用意されている、mpc_powは、そのまま使用するには問題があることがわかりました。
説明には、a^b =
exp(b*ln(a))となっているので間違いないのですが、a と b
が複素数の時、Imaginary部が両方ともゼロ時で aのreal部がマイナスの時は答えのreal部はゼロにならなければなりませんが、意味不明な値が入ります。
もう一つの問題は、乗数 b の値に、**.5 の様に
．５
の値になった時は、整数部の乗数*√の計算なのですがこの時は、realかImaginaryに意味不明な値が値が入ります。
c=a^b
の複素数計算の時、aとb両方の虚数部に0が発生する時は別途正しい答えがでるルーチンを作成する必要があります。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls,
VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs,
VCLTee.Chart, System.Diagnostics;
type
TForm1 = class(TForm)
Button1: TButton;
Memo1: TMemo;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
Chart1: TChart;
Series1: TLineSeries;
Series2: TLineSeries;
Series3: TPointSeries;
Series4: TPointSeries;
Series5: TLineSeries;
Series6: TLineSeries;
CheckBox1: TCheckBox;
CheckBox2: TCheckBox;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure FormClose(Sender: TObject; var Action: TCloseAction);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
uses system.Math, System.VarCmplx, Velthuis.BigIntegers,mp_real, mp_cmplx, mp_types, mp_base;
{$R *.dfm}
type
DArray = array of double;
var
xt, yt : Darray; // x,y データー akima補間用
m, t : array of mp_float; // m,t akima補間用
BM : array of mp_float; // ベルヌーイ数配列
FA : array of mp_float; // 階乗配列
PVG : array of mp_float; // +v Γ
MVG : array of mp_float; // -v Γ
zero, one, two, four : mp_float;
three, pai, log_2pis2 : mp_float;
const
KMmax = 250; // KM max 250
Vmax = 100; // v 次数 max
GL = 9; // グラフ基本点数
//------------------------------------------------------------------------------
NB = 120; // ベルヌーイ数 配列数 NB + 1
var
NumeratorString : array[0..NB] of string; // 分子
DenominatorString : array[0..NB] of string; // 分母
// 最大公約数 ユークリッドの互除法 BigInteger
function gcd_BigInteger(x, y: BigInteger): BigInteger;
var
t : BigInteger;
begin
while y <> 0 do begin
t := x mod y;
x := y;
y := t;
end;
result := x;
end;
// ベルヌーイ数
// Akiyama-Tanigawa algorithm
// BigInteger
// 文字配列出力
procedure Bernoulli_number_BigInteger;
const
n = (NB + 1) * 2;
var
m, j, k : integer;
a : array of BigInteger; // 分子
b : array of BigInteger; // 分母
tmpN : BigInteger; // 分子
tmpD : BigInteger; // 分母
gcd : BigInteger; // 最大公約数
b0 : BigInteger;
begin
setlength(a, n + 1);
setlength(b, n + 1);
k := 0;
for m := 0 to n do begin
a[m] := 1; // 分子 初期値
b[m] := (m + 1); // 分母 初期値
for j := m - 1 downto 0 do begin
tmpN := a[j] * b[j + 1] - a[j + 1] * b[j]; // 分子
tmpN := tmpN * (j + 1); // 〃
tmpD := b[j] * b[j + 1]; // 分母
gcd := gcd_BigInteger(tmpN, tmpD); // 最大公約数
a[j] := tmpN div gcd;
b[j] := tmpD div gcd;
end;
if (m > 0) and (m mod 2 = 0) then begin
b0 := b[0];
b0 := b0 * m * (m -1); // m ベルヌーイ数No
NumeratorString[k] := a[0].tostring;
DenominatorString[k] := b0.tostring;
inc(k);
end;
end;
end;
//------------------------------------------------------------------------------
// ログガンマ多倍長
procedure log_GammaMul(var x, ans : mp_float);
var
v, w : mp_float;
tmp, tmp0, s : mp_float;
i : integer;
begin
mpf_init2(v, w);
mpf_init3(tmp, tmp0, s);
mpf_set1(v);
mpf_set_int(tmp, NB);
while mpf_is_lt(x, tmp) do begin
mpf_mul(v, x, v);
mpf_add(x, one, x);
end;
mpf_mul(x, x, tmp); // x^2
mpf_div(one, tmp, w); // w = 1 / x^2
mpf_set0(s);
for i := NB downto 1 do begin
mpf_add(s, BM[i], tmp); // tmp = s + B[i]
mpf_mul(tmp, w, s); // s = tmp * w
end;
mpf_add(s, BM[0], tmp); // tmp = s + B[0]
mpf_div(tmp, x, s); // s = (s + B[0]) / x
mpf_add(s, log_2pis2, s); // s = s + ln(2π)/2
mpf_ln(v, tmp); // ln(v)
mpf_sub(s, tmp, s); // s := s - ln(v)
mpf_sub(s, x, s); // s := s - x
mpf_div(one, two, tmp); // tmp = 1/2
mpf_sub(x, tmp, tmp0); // tmp0 = x - 1/2
mpf_ln(x, tmp); // ln(x)
mpf_mul(tmp0, tmp, tmp0); // tmp0 = (x - 1/2) * ln(x)
mpf_add(s, tmp0, ans); // ans = s + (x - 1/2) * ln(x)
mpf_clear2(v, w);
mpf_clear3(tmp, tmp0, s);
end;
// 多倍長ガンマ
// xの値が 0 と負整数の時Γは∞になるのですが処理をしていませんのでエラーになります。
// ケルビンの次数が整数の時は使用されません。
procedure gammaMul(var x, ans: mp_float);
var
tmp, tmp0, logG : mp_float;
begin
mpf_init3(tmp, tmp0, logG);
if mpf_is_lt(x, zero) then begin
mpf_mul(pai, x, tmp); // x*π
mpf_sin(tmp, tmp0); // sin(πx);
mpf_sub(one, x, tmp); // 1-x
log_GammaMul(tmp, logG); // loggamma(1-x);
mpf_exp(logG, logG); // exp(logG)
mpf_div(pai, tmp0, tmp); // π/sin(πx)
mpf_div(tmp, logG, ans); // ans = π/(sin(πx) * logG(1-x))
end
else begin
log_GammaMul(x, logG); // logG
mpf_exp(logG, ans); // exp(logG)
end;
mpf_clear3(tmp, tmp0, logG);
end;
//------------------------------------------------------------------------------
// 階乗 多倍長
procedure factorialMul(n : integer; var ans: mp_float);
label
EXT;
var
i : integer;
bi : mp_float;
begin
mpf_init(bi);
mpf_set1(ans);
mpf_copy(two, bi);
if n <= 1 then begin
goto EXT;
end;
for i := 2 to n do begin
mpf_mul(ans, bi, ans);
mpf_add(bi, one, bi);
end;
EXT:
mpf_clear(bi);
end;
//------------------------------------------------------------------------------
// kelvin(x) 多倍長
// X 複素数 演算の都合上複素数にしてありります。
// kelvin関数のkeluin(x)のxの値は実数です。
// v 次数
// jv(xe^(iπ3/4))
procedure kelvin(var v : mp_float; var x, ri: mp_complex);
var
k : integer;
s, x24k, tmp, tmp0, tmp1 : mp_complex;
ixc, xs2 : mp_complex;
kd, nd, vk : mp_float;
khg, kf : mp_float;
tmf, tmf0 : mp_float;
sb : mp_complex;
begin
mpc_init5(s, x24k, tmp, tmp0, tmp1);
mpc_init3(ixc, xs2);
mpf_init2(khg, kf);
mpf_init3(kd, nd, vk);
mpf_init2(tmf, tmf0);
mpc_init(sb);
mpc_set0(s); // Σ=0
mpc_set0(sb);
mpc_div_mpf(x, two, xs2); // x / 2
mpc_mul(xs2, xs2, tmp); // (x^2)/ 4
mpf_copy(tmp.re, ixc.im);
mpf_copy(tmp.im, ixc.re); // i(x^2)/4
mpc_set1(x24k);
for k := 0 to KMmax do begin
mpf_set1(nd);
mpf_set_int(kf, k); // kf = k
mpf_add(v, kf, tmf0); // k + v
mpf_add(tmf0, one, vk); // vk = k + v + 1;
if mpf_is_lt(vk, zero) then begin // vk < 0 時 nxが整数か確認
mpf_int(vk, tmf); // int(vk);
mpf_sub(vk, tmf, nd); // vk - int(vk) vkが負の整数だったら vk = 0
end;
if mpf_is_ne(vk, zero) and mpf_is_ne(nd, zero) then begin // vkが負の整数の時は計算しない
if mpf_is_ge(v, zero) then
mpf_copy(PVG[k], tmf)
else
mpf_copy(MVG[k], tmf);
// GammaMul(vk, tmf); // Γ(n+k+1)
mpf_mul(FA[k], tmf, khg); // k!Γ(n+k+1) vkが0,負の整数の時±∞
// mpc_set_mpf(kc, kf, zero); // kc = k + 0i 複素数
// mpc_pow(ixc, kc, x24k); // (i(x^2)/4)^k
mpc_div_mpf(x24k, khg, tmp0); // ((i(x^2)/4)^k)/(k!Γ(v+k+1))
mpc_add(s, tmp0, s); // Σ
mpc_sub(s, sb, tmp0);
if mpc_is0(tmp0) then break;
mpc_copy(s, sb);
end;
mpc_mul(x24k, ixc, x24k);
end;
mpf_mul(pai, three, tmf); // 3*π
mpf_div(tmf, four, tmf0); // 3*π/4
mpc_set_mpf(tmp, zero, tmf0); // i(3π/4)
mpc_exp(tmp, tmp1); // e~i(3π/4)
mpc_mul(tmp1, xs2, tmp1); // (x/2)e^i(3π/4)
mpc_set_mpf(tmp, v, zero); // v + 0i
// x が0で次数vが負数の時power演算ゼロでの除算防止
if mpc_is0(x) and mpf_is_lt(v, zero) then // V<0 x=0 時は無限大になるので計算しない
else begin
mpc_pow(tmp1, tmp, tmp0); // ((x/2)e^i(3π/4))^v
mpc_mul(s, tmp0, s); // ((x/2)(e^i(3π/4)))^v * Σ
end;
mpc_copy(s, ri);
mpc_clear5(s, x24k, tmp, tmp0, tmp1);
mpc_clear2(ixc, xs2);
mpf_clear2(khg, kf);
mpf_clear3(kd, nd, vk);
mpf_clear2(tmf, tmf0);
mpc_clear(sb);
end;
// akima m,t テーブル作成
// x[] xデーター配列
// y[] yデーター配列
// m[] m係数テーブル
// t[] t係数テーブル
procedure akima_table;
var
ii, n : integer;
a, b, half, tmf, tmf0 : mp_float;
ytm, xtm : array of mp_float;
tmf1 : mp_float;
begin
n := high(xt) + 1;
setlength(ytm, n);
setlength(xtm, n);
for ii := 0 to n - 1 do begin
mpf_init(ytm[ii]);
mpf_init(xtm[ii]);
end;
mpf_init5(a, b, half, tmf, tmf0);
mpf_init(tmf1);
mpf_set_dbl(half, 1 / 2);
// mpf_set_int(tow, 2);
// mpf_set0(zero);
for ii := 0 to n -1 do begin
mpf_set_dbl(xtm[ii], xt[ii]);
mpf_set_dbl(ytm[ii], yt[ii]);
end;
// shift data by + 2 in the array and compute the secants
// also calculate extrapolated and end point secants
// 傾斜α両端を除く Δy/Δx
for ii := 0 to n - 2 do begin
mpf_sub(ytm[ii + 1], ytm[ii], tmf);
mpf_sub(xtm[ii + 1], xtm[ii], tmf0);
mpf_div(tmf, tmf0, m[ii + 2]);
end;
// for ii := 0 to n - 2 do
// m[ii + 2] := (yt[ii + 1] - yt[ii]) / (xt[ii + 1] - xt[ii]);
// 端点傾斜処理
mpf_mul(two, m[2], tmf);
mpf_sub(tmf, m[3], m[1]);
// m[1] := 2 * m[2] - m[3];
mpf_mul(two, m[1], tmf);
mpf_sub(tmf, m[2], m[0]);
// m[0] := 2 * m[1] - m[2];
mpf_mul(two, m[n], tmf);
mpf_sub(tmf, m[n - 1], m[n + 1]);
// m[n + 1] := 2 * m[n] - m[n - 1];
mpf_mul(two, m[n + 1], tmf);
mpf_sub(tmf, m[n], m[n + 2]);
// m[n + 2] := 2 * m[n + 1] - m[n];
// 各ポイントの傾斜係数計算
for ii := 0 to n - 1 do begin
mpf_sub(m[ii + 3],m[ii + 2],tmf0);
mpf_abs(tmf0, a);
// a := abs(m[ii + 3] - m[ii + 2]);
mpf_sub(m[ii + 1], m[ii], tmf0);
mpf_abs(tmf0, b);
// b := abs(m[ii + 1] - m[ii]);
mpf_add(a, b, tmf1);
if mpf_is_ne(tmf1, zero) then begin
mpf_mul(a, m[ii + 1], tmf);
mpf_mul(b, m[ii + 2], tmf0);
mpf_add(tmf, tmf0, tmf);
mpf_div(tmf, tmf1, t[ii]);
end
else begin
mpf_add(m[ii + 2], m[ii + 1], tmf);
mpf_mul(half, tmf, t[ii]);
end;
{
if (a + b) <> 0 then begin
t[ii] := (a * m[ii + 1] + b * m[ii + 2]) / (a + b);
end
else
t[ii] := half * (m[ii + 2] + m[ii + 1]);
}
end;
for ii := 0 to n - 1 do begin
mpf_clear(ytm[ii]);
mpf_clear(xtm[ii]);
end;
mpf_clear5(a, b, half, tmf, tmf0);
mpf_clear(tmf1);
end;
// akima 補間値計算
// xx xの値
// x[] xデーター配列
// y[] yデーター配列
// m[] m係数テーブル
// t[] t係数テーブル
// result 補間値y'
function akima_Interpolation(xx: double): double;
var
iB, iM, iT: integer;
a, b, tmf, tmf0 : mp_float;
c, d, e, f, tmf1 : mp_float;
three : mp_float;
begin
mpf_init4(a, b, tmf, tmf0);
mpf_init5(c, d, e, f, tmf1);
mpf_init(three);
mpf_set_int(three, 3);
iB := low(xt); // x[] bottom 配列no
iT := high(xt); // x[] top配列No
// xx値の上下の配列xの配列番号を探す
// XX<x[iB]の場合一番下の区間 XX>x[iT]の場合一番上の区間
while (iT - iB) > 1 do begin
iM := (iB + iT) div 2; // middle配列no
if xt[iM] > xx then
iT := iM
else
iB := iM;
end;
mpf_set_dbl(b, xt[iT] - xt[iB]);
// b := xt[iT] - xt[iB]; // 区間のxの変化量
mpf_set_dbl(a, xx - xt[iB]);
// a := xx - xt[iB]; // x[iB]からのxの値
// 3次akima spline 計算
mpf_set_dbl(c, yt[iB]); // c = yt[ib]
mpf_mul(t[iB], a, d); // d = t[ib] * a
mpf_mul(three, m[iB + 2], tmf); // 3 * m[iB + 2]
mpf_mul(two, t[ib], tmf0); // 2 * t[iB]
mpf_sub(tmf, tmf0, tmf1); // 3 * m[iB + 2] - 2 * t[iB]
mpf_sub(tmf1, t[iB + 1], tmf); // 3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]
mpf_mul(tmf, a, tmf); // (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a
mpf_mul(tmf, a, tmf); // (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a * a
mpf_div(tmf, b, e); // (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a * a / b
mpf_add(t[iB], t[iB + 1], tmf); // t[iB] + t[iB + 1]
mpf_mul(two, m[iB + 2], tmf0); // 2 * m[iB + 2]
mpf_sub(tmf, tmf0, tmf); // t[iB] + t[iB + 1] - 2 * m[iB + 2]
mpf_mul(tmf, a, tmf); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a
mpf_mul(tmf, a, tmf); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a
mpf_mul(tmf, a, tmf); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a * a
mpf_mul(b, b, tmf0); // b * b
mpf_div(tmf, tmf0, f); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a * a / (b * b)
mpf_add(c, d, tmf); // c + d
mpf_add(tmf, e, tmf); // c + d + e
mpf_add(tmf, f, tmf); // c + d + e + f
result := mpf_todouble(tmf);
{
result := yt[iB]
+ t[iB] * a
+ (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a * a / b
+ (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a * a / (b * b);
}
mpf_clear4(a, b, tmf, tmf0);
mpf_clear5(c, d, e, f, tmf1);
mpf_clear(three);
end;
// 計算
// xの値が大きくなると誤差が大きくなります。
// ta[] グラフ作成用テーター計算点
procedure TForm1.Button1Click(Sender: TObject);
label
EXT;
const
x0m = 1e-50; // ゼロ近傍値 infinity 符号設定用
ta : array[0..GL - 1] of double = (0.08, 0.14, 0.23, 0.46, 0.86, 1.5, 2.5, 3.2, 4);
YPM = 1E304; // Double 最大値制限 オーバフロー対策
YMM = -YPM;
var
ch, i, xi: integer;
berx, beix: double;
berxe, beixe: double;
xin, vin, xv, rk, ik: double;
xmin, xmax, dx, dxf : double;
ymin, ymax: double;
berl : Darray;
beil : Darray;
beru : Darray;
beiu : Darray;
xl : Darray;
xu : Darray;
xm, vm, xvm, ixm: mp_float;
nd, tmf : mp_float;
ri : mp_complex;
GCF : integer;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
mm, ss, ms : integer;
xc, xcb : mp_complex;
GU, GS : integer; // グラフ作成時 推定点数
k : integer;
vk, avm, tmf0 : mp_float;
ix : double;
// double to mpc グラフ計算用
procedure xvtoxc(xv, ia : double; var xc : mp_complex);
begin
mpf_set_dbl(xvm, xv);
mpf_set_dbl(tmf, ia);
mpc_set_mpf(xc, xvm, tmf);
end;
// Double 最大値制限
function maxmin(x : double): double;
begin
result := x;
if x > YPM then result := YPM;
if x < YMM then result := YMM;
end;
begin
memo1.Clear;
val(labelededit1.Text, vin, ch);
if ch <> 0 then begin
application.MessageBox('次数vの値に間違いがあります。','注意', 0);
exit;
end;
if abs(vin) > Vmax then begin
application.MessageBox('次数vの値が計算範囲外です。','注意', 0);
exit;
end;
val(labelededit2.Text, xin, ch);
if ch <> 0 then begin
application.MessageBox('xの値に間違いがあります。','注意', 0);
exit;
end;
if abs(xin) > 100 then begin
application.MessageBox('xが100を越えると条件によって誤差が大きくなります。','注意', 0);
end;
mpf_init4(xm, vm, xvm, ixm);
mpf_init2(nd, tmf);
mpf_init3(vk, avm, tmf0);
mpc_init3(ri, xc, xcb);
mpf_set0(zero);
ix := 0;
mpf_set0(ixm);
mpf_read_decimal(vm, PAnsiChar(ansistring(labelededit1.Text + #00)));
mpf_read_decimal(xm, PAnsiChar(ansistring(labelededit2.Text + #00)));
mpc_set_mpf(xcb, xm, ixm); // xcb 計算用 xの複素数
series1.Clear;
series2.Clear;
series3.Clear;
series4.Clear;
series5.Clear;
series6.Clear;
memo1.Lines.Append('v = ' + floatTostr(vin) + ' x = ' + floatTostr(xin));
application.ProcessMessages;
rk := 0;
ik := 0;
mpf_abs(vm, avm);
for k := 0 to KMmax do begin
mpf_set_int(tmf, k); // k
mpf_add(tmf, avm, tmf0); // v + k
mpf_add(tmf0, one, vk); // vk= v + k + 1
gammaMul(vk, PVG[k]); // Γ(n+k+1)
end;
mpf_chs(avm, avm); // -v
for k := 0 to KMmax do begin
mpf_set1(nd);
mpf_set_int(tmf, k); // k
mpf_add(tmf, avm, tmf0); // -v + k
mpf_add(tmf0, one, vk); // vk= -v + k + 1
if mpf_is_lt(vk, zero) then begin // vk < 0 時 nxが整数か確認
mpf_int(vk, tmf); // int(vk);
mpf_sub(vk, tmf, nd); // vk - int(vk) vkが負の整数だったら nd = 0
end;
if mpf_is_ne(vk, zero) and mpf_is_ne(nd, zero) then // vkが負の整数の時は計算しない
gammaMul(vk, MVG[k]) // Γ(n+k+1)
else
mpf_set0(MVG[k]); // Γ(n+k+1) = 0
end;
// ゼロ近傍の計算符号設定
xvtoxc(x0m, ix, xc); // x double to mpc
kelvin(vm, xc, ri); // ゼロ近辺のプラス側x計算
if mpf_is_ne(nd, zero) then begin // vが-0以下で整数でなく
if mpf_is_ge(ri.re, zero) then rk := infinity // x=0時の無限大±符号設定
else rk := -infinity;
if mpf_is_ge(ri.im, zero) then ik := infinity
else ik := -infinity;
end;
mpf_int(vm, tmf); // int(vm)
mpf_sub(vm, tmf, nd); // nd = vm - int(v)
StopWatch := TStopwatch.StartNew;
// 表示値の計算
kelvin(vm, xcb, ri); // xcb 複素数
// x=0 v < 0 v = 非整数 の場合 ±∞
if mpc_is0(xcb) and mpf_is_lt(vm, zero) and mpf_is_ne(nd, zero) then begin
berxe := rk;
beixe := ik;
memo1.Lines.Append('berv(x) = ' + floatTostr(berxe)); // 数値表示
memo1.Lines.Append('beiv(x) = ' + floatTostr(beixe));
end
else begin
memo1.Lines.Append( string('berv(x) = ' + mpf_decimal(ri.re, 50)));
memo1.Lines.Append( string('beiv(x) = ' + mpf_decimal(ri.im, 50)));
berxe := mpf_todouble(ri.re);
beixe := mpf_todouble(ri.im);
end;
StopWatch.Stop;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
ms := ElapsedMillseconds * (GL + 1) * 2 + 1000;
mm := ms div 60000;
ss := (ms mod 60000) div 1000;
memo1.Lines.Append('グラフ表示に約' + inttostr(mm) + '分' + inttostr(ss) + '秒必要です。');
if checkbox2.Checked = true then begin // グラフ無だったら終了
Chart1.Canvas.Font.Style := [fsBold];
Chart1.Canvas.Font.size := 8;
Chart1.Canvas.TextOut(170, 115,'グラフ無し');
goto EXT;
end;
// 最大値最小値の検索とグラフデーター作成
xi := round(xin);
xmin := xi - 4;
GCF := 0;
if (Xin >= -2) and (xin <= 2) then GCF := 1;
if (xin >= -3) and (xin <= -2) then GCF := 2;
if (xin >= 2) and (xin <= 3) then GCF := 3;
if (xin >= -4) and (xin <= -3) then GCF := 4;
if (xin >= 3) and (xin <= 4) then Gcf := 5;
case GCF of
0: xmin := xi - 4;
1: xmin := -4;
2: xmin := -5;
3: xmin := -3;
4: xmin := -6;
5: xmin := -2;
end;
xmax := xmin + 8;
case GCF of
0 : begin
setlength(berl, GL + GL);
setlength(beil, GL + GL);
setlength(xt, GL + GL); setlength(yt, GL + GL);
setlength(xl, GL + GL);
end;
1, 2, 3, 4, 5:
begin
setlength(berl, GL); setlength(beru, GL);
setlength(beil, GL); setlength(beiu, GL);
setlength(xt, GL); setlength(yt, GL);
setlength(xl, GL); setlength(xu, GL);
end;
end;
dxf := 0.1;
dx := 0.1;
GU := 40;
GS := 40;
case GCF of
0 :
begin
dx := (xmax - xmin) / (Gl + GL - 1);
for i := 0 to GL + GL - 1 do xl[i] := dx * i + xmin;
xl[0] := xl[0] + dxf;
xl[GL + GL - 1] := xl[GL + GL - 1] - dxf;
GS := 80;
end;
else
begin
for i := 0 to GL - 1 do begin
xu[i] := ta[i];
xl[GL - i - 1] := -ta[i];
end;
end;
end;
case GCF of
2 : begin dx := 5 / 4; dxf := 3 / 4; GS := 50; GU := 30; end;
3 : begin dx := 3 / 4; dxf := 5 / 4; GS := 30; GU := 50; end;
4 : begin dx := 6 / 4; dxf := 2 / 4; GS := 60; GU := 20; end;
5 : begin dx := 2 / 4; dxf := 6 / 4; GS := 20; GU := 60; end;
end;
if GCF >= 2 then begin
for i := 0 to Gl - 1 do xl[i] := xl[i] * dx;
for i := 0 to Gl - 1 do xu[i] := xu[i] * dxf;
end;
// グラフ用データー作成
ymin := 0;
ymax := 0;
case GCF of
0 : begin
for i := 0 to GL + GL - 1 do begin
xv := xl[i];
xvtoxc(xv, ix, xc);
kelvin(vm, xc, ri);
berl[i] := maxmin(mpf_todouble(ri.re));
beil[i] := maxmin(mpf_todouble(ri.im));
if berl[i] > ymax then ymax := berl[i];
if beil[i] > ymax then ymax := beil[i];
if berl[i] < ymin then ymin := berl[i];
if beil[i] < ymin then ymin := beil[i];
end;
end;
1, 2, 3, 4, 5:
for i := 0 to GL - 1 do begin
xv := xl[i];
xvtoxc(xv, ix, xc);
kelvin(vm, xc, ri);
berl[i] := maxmin(mpf_todouble(ri.re));
beil[i] := maxmin(mpf_todouble(ri.im));
if berl[i] > ymax then ymax := berl[i];
if beil[i] > ymax then ymax := beil[i];
if berl[i] < ymin then ymin := berl[i];
if beil[i] < ymin then ymin := beil[i];
xv := xu[i];
xvtoxc(xv, ix, xc);
kelvin(vm, xc, ri);
beru[i] := maxmin(mpf_todouble(ri.re));
beiu[i] := maxmin(mpf_todouble(ri.im));
if beru[i] > ymax then ymax := beru[i];
if beiu[i] > ymax then ymax := beiu[i];
if beru[i] < ymin then ymin := beru[i];
if beiu[i] < ymin then ymin := beiu[i];
end;
end;
// 指定値の値制御
if berxe > ymax then berxe := ymax;
if berxe < ymin then berxe := ymin;
if beixe > ymax then beixe := ymax;
if beixe < ymin then beixe := ymin;
series3.AddXY(xin, berxe);
series4.AddXY(xin, beixe);
if checkbox1.Checked = true then
case GCF of
0:
begin
for i := 0 to GL + GL - 1 do begin
series1.AddXY(xl[i], berl[i]);
series2.AddXY(xl[i], beil[i]);
end;
end;
1, 2, 3, 4, 5 :
begin
for i := 0 to GL - 1 do begin
series1.AddXY(xl[i], berl[i]);
series2.AddXY(xl[i], beil[i]);
series5.AddXY(xu[i], beru[i]);
series6.AddXY(xu[i], beiu[i]);
end;
end;
end;
if checkbox1.Checked = false then
// グラフ計算
case GCF of
0:
begin
for i := 0 to GL + GL - 1 do begin
xt[i] := xl[i];
yt[i] := berl[i];
end;
akima_table;
dx := (xt[GL + GL - 1] - xt[0]) / GS;
for i := 0 to GS do begin
xv := dx * i + xt[0];
berx := maxmin(akima_Interpolation(xv));
series1.AddXY(xv, berx);
end;
for i := 0 to GL + GL - 1 do yt[i] := beil[i];
akima_table;
for i := 0 to GS do begin
xv := dx * i + xt[0];
beix := maxmin(akima_Interpolation(xv));
series2.AddXY(xv, beix);
end;
end;
1, 2, 3, 4, 5 :
begin
for i := 0 to GL- 1 do begin
xt[i] := xl[i];
yt[i] := berl[i];
end;
akima_table;
dx := xt[0] / GS;
for i := GS downto 1 do begin
xv := dx * i;
berx := maxmin(akima_Interpolation(xv));
series1.AddXY(xv, berx);
end;
for i := 0 to GL- 1 do yt[i] := beil[i];
akima_table;
for i := GS downto 1 do begin
xv := dx * i;
beix := maxmin(akima_Interpolation(xv));
series2.AddXY(xv, beix);
end;
if mpf_is0(xm) then begin
// series1.AddXY(0, herxe);
// series2.AddXY(0, heixe);
series5.AddXY(0, berxe);
series6.AddXY(0, beixe);
end;
for i := 0 to GL- 1 do begin
xt[i] := xu[i];
yt[i] := beru[i];
end;
akima_table;
dx := xt[GL - 1] / GU;
for i := 1 to GU do begin
xv := dx * i;
berx := maxmin(akima_Interpolation(xv));
series5.AddXY(xv, berx);
end;
for i := 0 to GL- 1 do yt[i] := beiu[i];
akima_table;
for i := 1 to GU do begin
xv := dx * i;
beix := maxmin(akima_Interpolation(xv));
series6.AddXY(xv, beix);
end;
end;
end;
EXT:
mpf_clear4(xm, vm, xvm, ixm);
mpf_clear2(nd, tmf);
mpc_clear3(ri, xc, xcb);
mpf_clear3(vk, avm, tmf0);
end;
procedure TForm1.FormCreate(Sender: TObject);
var
i : integer;
N, D, tmp : mp_float;
begin
mpf_set_default_decprec(180); // 有効桁数180桁 50桁の精度に必要です。
setlength(BM, NB + 1); // ベルヌーイ数配列
setlength(FA, KMmax + Vmax + 1); // K1配列
setlength(PVG, KMmax + Vmax + 2); // +vΓ
setlength(MVG, KMmax + Vmax + 2); // -vΓ
setlength(t, GL + GL); // akima 補間値計算 配列 t
setlength(m, GL + GL + 3); // akima 補間値計算 配列 m
for i := 0 to NB do mpf_init(BM[i]);
for i := 0 to KMmax + Vmax do mpf_init(FA[i]);
for i := 0 to KMmax + Vmax + 1 do mpf_init(PVG[i]);
for i := 0 to KMmax + Vmax + 1 do mpf_init(MVG[i]);
for i := 0 to GL + GL - 1 do mpf_init(t[i]);
for i := 0 to GL + GL + 2 do mpf_init(m[i]);
mpf_init3(N, D, tmp);
mpf_init4(zero, one, two, four);
mpf_init3(three, pai, log_2pis2);
mpf_set0(zero);
mpf_set1(one);
mpf_set_int(two, 2);
mpf_set_int(three, 3);
mpf_set_int(four, 4);
mpf_set_pi(pai);
mpf_mul(pai, two, tmp); // 2π
mpf_ln(tmp, tmp); // ln(2π)
mpf_div(tmp, two, log_2pis2); // ln(2π)/2
Bernoulli_number_BigInteger; // ベルヌーイ数作成
for i := 0 to NB do begin
mpf_read_decimal(N, PAnsiChar(ansistring(NumeratorString[i] + #00)));
mpf_read_decimal(D, PAnsiChar(ansistring(DenominatorString[i] + #00)));
mpf_div(N, D, BM[i]);
end;
for i := 0 to KMmax + Vmax do begin
factorialMul(i, N);
mpf_copy(N, FA[i]);
end;
memo1.Clear;
mpf_clear3(N, D, tmp);
end;
procedure TForm1.FormClose(Sender: TObject; var Action: TCloseAction);
var
i : integer;
begin
for i := 0 to NB do mpf_clear(BM[i]);
for i := 0 to KMmax + Vmax do mpf_clear(FA[i]);
for i := 0 to KMmax + Vmax + 1 do mpf_clear(PVG[i]);
for i := 0 to KMmax + Vmax + 1 do mpf_clear(MVG[i]);
for i := 0 to GL + GL - 1 do mpf_clear(t[i]);
for i := 0 to GL + GL + 2 do mpf_clear(m[i]);
mpf_clear4(zero, one, two, four);
mpf_clear3(three, pai, log_2pis2);
end;
end.
kelvin_function_Mult_of_1st_kind.zip
三角関数、逆三角関数、その他関数 に戻る