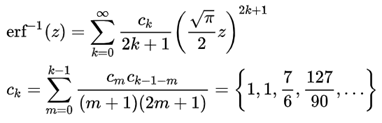
逆誤差関数 (Extended Double)
Extended、Doubleの計算の計算の精度確認です。
実際の使用においての精度は、Doubleで十分だと思います。
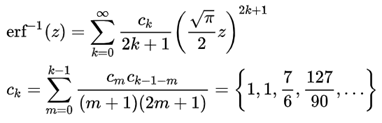
逆誤差関数の上記計算をそのまま実行すると、Ckのk値が大きくなり、Ckの値を求めるのに非常に時間がかかります。
C、C++に組み込まれているerfinv関数では通常のLong Doubleの関数となっており近似計算をしています。
近似値は、分子と、分母に分けて、zの値の大きさに応じて何種類かに分けて計算しています。
逆誤差関数にあるものをは、多倍長計算となっているので、Extended(Long
Double) Win32(x86)とDouble Win64(x64)のプログラムに変換してみました。
Win32 と
Win64の切り替えは、コンパイラをWin32にするか、Win64にするかです。
DoubleとExtended(Long Duble)の計算精度は次の様になります。
Double
5.0 * 10^-324 ~ 1.7 * 10^308 15~16桁
Extended
3.6 * 10^-4951 ~ 1.1 * 10^4932 19~20桁
実際の計算では、Extendedで表示されるのは、18桁でDoubleでは16桁程度です。
通常のFloatToStrでは両方とも15桁までしか表示されません。
18桁表示する為には、FloatToStrFを使用する必要があります。
演算の精度を比較する為に、逆誤差関数のなかりC++から多倍長に変換したもの比較出来るように同じものを組み込んでみました。
ついでに、JavaScriptで組まれたプログラムを見つけたので、これも比較の為に、変換して組み込んでみました。
C++のものも、JavaScriptのものも、Long
Doubleとなっているので、Win32モードの方が精度が高くなります。
近似値用のデーターはC++は20桁、JavaScriptは15~18桁程度となっています。
何桁まで正しい値を返すかは、多倍長での計算と比較すれば良いでしょう、元の近似用の値は同じですが、多倍長計算の方が精度が高い答えとなります。
参考の為に誤差関数erf(z)のExtended(long double)の計算も組み込んでみました、これは別ユニットにしてあります。
erf(z)の計算はx86モードの時 z= 4.7 が最大値とり、x64モードではdouble演算となり z= 4 が最大値となります。
実際にはもう少し大きな値を計算出来るのですが、演算誤差により正しい値を返さなくなります。
プログラム
Biginteger & Bigdecimal の組み込み方は第1種ケルビン関数を参照して下さい。
注 textからDoubleに変換するとき、'0.999999・・・9'の'9'の値が続く場合、1に変換されないで、1.000000000000000222044604925031になるようです。
1より大きな値となります。
普通は、'0.999999・・・9の様な値を入れることは無いので、バグとして認識されていないのでしょう。
対策として一度 FlotToStrでTextにして再度読み込んで、1になるようにしています。
Main.pas
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, system.UITypes, Soap.TypeTrans;
type
TForm1 = class(TForm)
CalcBtn: TButton;
Memo1: TMemo;
yEdit: TLabeledEdit;
erfBtn: TButton;
zEdit: TLabeledEdit;
procedure CalcBtnClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure erfBtnClick(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
epsilon : extended;
implementation
{$R *.dfm}
uses system.Math, erf, Velthuis.BigIntegers, Velthuis.Bigdecimals;
const
DPS = 50;
//--------------------------------- Ln(x)---------------------------------------
// x = m * 2^n のnの値と2^nの値を戻します
// result = n
// ta = 2^n
// m = x / 2^n
function frexpa(x: bigdecimal; var ta: biginteger): integer;
var
tb: biginteger;
xi, one: bigdecimal;
n, j, s, pcs : integer;
begin
pcs := BigDecimal.DefaultPrecision;
one := '1';
one := one.RoundToPrecision(pcs);
xi := x; // x保存
if xi < one then x := one / x; // 1より小さかったら逆数
ta := '1';
n := 0;
j := 0; // シフト回数クリア
ta := '1'; // ta初期値
s := 4096; // s=4^i i = 6
repeat
while x > ta do begin
biginteger.ShiftLeft(ta, s, tb); // s分左シフト
ta := tb;
inc(j); // シフト回数インクリメント
end;
if (s > 1) and (j > 0) then begin // ta > x になったら
dec(j); // シフト回数デクリメント
biginteger.Shiftright(ta, s, tb); // s分右シフト
ta := tb;
end;
n := n + s * j; // 2^nのn計算
j := 0; // シフト回数クリア
s := s shr 2; // sの値を1/4にする 右へ2ビットシフト
// s := s div 4; // sの値を1/4にする
until s = 0; // s= ...16, 4, 1, 0
if xi < one then begin // より小さかったら
n := -n + 1; // 2^nのn値負数
biginteger.Shiftright(ta, 1, tb); // 上式+1により右シフト
ta := tb;
end;
result := n // ta = 2^n
end;
// 小さい値のlog計算
// xi 実数
// dpcs 有効桁数
// ans log値
// 戻り値 Loopオーバーフロー 無し true 有り false
// loop制限の無い場合 1e-4~1e4 が計算出来る範囲
// loop制限 5.8e-3 ~1.73e2 (kk=10000の場合)
function Log_11(x: bigdecimal; dpcs: integer; var ans: bigdecimal): boolean;
const
KK = 10000;
var
one, two, x1, x2, i, s, last: bigdecimal;
k : integer;
begin
result := true;
one := '1';
two := '2';
x1 := (x - one) / (x + one); // x1 = (x-1)/(x+1)
x2 := x1 * x1; // x1^2
x2 := x2.RoundToPrecision(dpcs);
i := one; // i=1
s := x1; // s初期値
k := 0; // 長ループ脱出用カウンタ0
repeat
x1 := x1 * x2; // x1^2n+1
x1 := x1.RoundToPrecision(dpcs);
i := i + two; // 2n+1
i := i.RoundToPrecision(dpcs);
last := s; // 判定用sの値保存
s := s + x1 / i; // Σs = s + x1^2n+1 / (2n+1)
s := s.RoundToPrecision(dpcs); // 収束判定の為指定有効桁数以下丸め
inc(k); // ループカウンタインクリメント
until (last = s) or (k > KK); // 収束判定
ans := two * s;
if k > kk then result := false;
end;
// loge(x) ln(x)
// 級数展開
// 1e±500000 程度が限度
// sm <xi< last の範囲外の場合 (0.7~xi~1.4) * 2^nに変換 xiが1に近いほど変換早い
function log_big(xi: bigdecimal): bigdecimal;
label
EXT;
const
KK = 10000;
var
LOG2, SQRT2, two, last, s, sm, one, one1, k2, a: bigdecimal;
k : integer;
kb, ta : biginteger;
pcsBack, dpcs : integer;
rmback : BigDecimal.RoundingMode;
begin
result := '0';
if xi <= result then begin
application.MessageBox('無効な値です。','注意',0);
exit;
end;
sm := '1e-2';
last := '5e1';
pcsBack := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ
rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ
dpcs := pcsBack + 5; // 指定精度 + α
BigDecimal.DefaultPrecision := dpcs;
BigDecimal.DefaultRoundingMode := rmNearesteven;
one := '1';
if xi = one then begin
goto EXT;
end;
if (xi > sm) and (xi < last) then begin // 0.01 < xi < 50の時はLog11計算
if Log_11(xi, dpcs, a) then begin // log11
result := a;
goto EXT;
end;
end;
one1 := '1e500000';
if xi < one then begin // xi < 1
last := one / xi; // 1 / xi
if last > one1 then begin // (1 / xi) > 1e500000
application.MessageBox('値が小さすぎます。','注意',0);
goto EXT;
end;
end;
if xi > one1 then begin // xi > 1e500000
application.MessageBox('値が大きすぎます。','注意',0);
goto EXT;
end;
xi := xi.RoundToPrecision(dpcs);
two := '2';
Log_11(two, dpcs, LOG2); // log(2)
SQRT2 := bigdecimal.Sqrt(two, dpcs * 2); // √2
k := frexpa(xi / SQRT2, ta); // x / √2 = m * 2^k ta = 2^k
kb := k;
k2 := ta; // 2^k integer to decimal
k2 := k2.RoundToPrecision(dpcs);
if k < 0 then begin // kが負数だったら
xi := xi * k2; // x * 2^k x=0.707~1.414 √2
xi := xi.RoundToPrecision(dpcs);
end
else begin
xi := xi / k2; // x / 2^k x=0.707~1.414 √2
end;
if xi <> one then begin // xi <> 1 なら
Log_11(xi, dpcs, s) // log(xi)
end
else s := '0'; // xi=1なら s=0
result := LOG2 * kb + s;
EXT:
result := result.RoundToPrecision(pcsBack);
BigDecimal.DefaultPrecision := pcsBack; // 除算演算精度復帰
BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰
end;
//----------------------------- errinv 10byte相当-------------------------------
// C++ライブラリより変換
// 元は Long Double 10byte演算でしたので多倍長演算を使用
// 近似計算用データーは20桁ありますが、誤差により18桁程度の精度となります。
// doubleでの計算でも15桁程度の精度は出ますが1に近い0.9999999999999999の場合無限大になります。
function Inverse_error_long_double(x : bigdecimal; var INF : integer): bigdecimal;
const
DPSLD = 30;
var
LN2 : bigdecimal;
A : array[0..7] of bigdecimal;
B : array[0..7] of bigdecimal;
C : array[0..7] of bigdecimal;
D : array[0..7] of bigdecimal;
E : array[0..7] of bigdecimal;
F : array[0..7] of bigdecimal;
abs_x, r, num, den : bigdecimal;
d1, d2 : bigdecimal;
i : integer;
begin
INF := 0;
if (x < -1) or (x > 1) then begin
result := 0;
exit;
end;
if (x = -1) then begin
INF := - 1;
exit;
end;
if (x = 1) then begin
INF := 1;
exit;
end;
bigdecimal.DefaultPrecision := DPSLD; // 除算30桁設定
LN2 := '6.931471805599453094172321214581e-1';
A[0] := '1.1975323115670912564578e0';
A[1] := '4.7072688112383978012285e1';
A[2] := '6.9706266534389598238465e2';
A[3] := '4.8548868893843886794648e3';
A[4] := '1.6235862515167575384252e4';
A[5] := '2.3782041382114385731252e4';
A[6] := '1.1819493347062294404278e4';
A[7] := '8.8709406962545514830200e2';
B[0] := '1.0000000000000000000e0';
B[1] := '4.2313330701600911252e1';
B[2] := '6.8718700749205790830e2';
B[3] := '5.3941960214247511077e3';
B[4] := '2.1213794301586595867e4';
B[5] := '3.9307895800092710610e4';
B[6] := '2.8729085735721942674e4';
B[7] := '5.2264952788528545610e3';
C[0] := '1.42343711074968357734e0';
C[1] := '4.63033784615654529590e0';
C[2] := '5.76949722146069140550e0';
C[3] := '3.64784832476320460504e0';
C[4] := '1.27045825245236838258e0';
C[5] := '2.41780725177450611770e-1';
C[6] := '2.27238449892691845833e-2';
C[7] := '7.74545014278341407640e-4';
D[0] := '1.4142135623730950488016887e0';
D[1] := '2.9036514445419946173133295e0';
D[2] := '2.3707661626024532365971225e0';
D[3] := '9.7547832001787427186894837e-1';
D[4] := '2.0945065210512749128288442e-1';
D[5] := '2.1494160384252876777097297e-2';
D[6] := '7.7441459065157709165577218e-4';
D[7] := '1.4859850019840355905497876e-9';
E[0] := '6.65790464350110377720e0';
E[1] := '5.46378491116411436990e0';
E[2] := '1.78482653991729133580e0';
E[3] := '2.96560571828504891230e-1';
E[4] := '2.65321895265761230930e-2';
E[5] := '1.24266094738807843860e-3';
E[6] := '2.71155556874348757815e-5';
E[7] := '2.01033439929228813265e-7';
F[0] := '1.414213562373095048801689e0';
F[1] := '8.482908416595164588112026e-1';
F[2] := '1.936480946950659106176712e-1';
F[3] := '2.103693768272068968719679e-2';
F[4] := '1.112800997078859844711555e-3';
F[5] := '2.611088405080593625138020e-5';
F[6] := '2.010321207683943062279931e-7';
F[7] := '2.891024605872965461538222e-15';
abs_x := x.Abs(x);
if abs_x < '0.85' then begin
d1 := '0.180625';
d2 := '0.25';
r := d1 - d2 * x * x;
num := A[7];
den := B[7];
for i := 6 downto 0 do begin
num := num * r + A[i];
den := den * r + B[i];
end;
num := num.RoundToPrecision(DPSLD);
den := den.RoundToPrecision(DPSLD);
result := x * num / den;
bigdecimal.DefaultPrecision := DPS; // 除算有効桁数元に戻し
exit;
end;
r := bigdecimal.Sqrt(LN2 - log_big(bigdecimal.One - abs_x));
if r <= '5.0' then begin
d1 := '1.6';
r := r - d1;
num := C[7];
den := D[7];
for i := 6 downto 0 do begin
num := num * r + C[i];
den := den * r + D[i];
end;
end
else begin
d2 := '5.0';
r := r - d2;
num := E[7];
den := F[7];
for i := 6 downto 0 do begin
num := num * r + E[i];
den := den * r + F[i];
end;
end;
num := num.RoundToPrecision(DPSLD);
den := den.RoundToPrecision(DPSLD);
result := num / den;
if x < '0' then
result := - result;
bigdecimal.DefaultPrecision := DPS; // 除算有効桁数元に戻し
end;
//------------------------------------------------------------------------------
// stdlib-js Standard library for JavaScript より変換
function inverse_error_js(x : extended): extended;
const
Y1 = 8.91314744949340820313e-2;
Y2 = 2.249481201171875;
Y3 = 8.07220458984375e-1;
Y4 = 9.3995571136474609375e-1;
Y5 = 9.8362827301025390625e-1;
var
sign, ax, qs, q, g, r : extended;
function rational_p1q1(x : extended): extended;
var
s1, s2 : extended;
begin
if x = 0.0 then begin
result := -0.0005087819496582806;
exit;
end;
s1 := -0.0005087819496582806 + (x * (-0.008368748197417368 + (x * (0.03348066254097446
+ (x * (-0.012692614766297404 + (x * (-0.03656379714117627 + (x * (0.02198786811111689
+ (x * (0.008226878746769157 + (x * (-0.005387729650712429 + (x * (0.0 + (x * 0.0)))))))))))))))));
s2 := 1.0 + (x * (-0.9700050433032906 + (x * (-1.5657455823417585 + (x * (1.5622155839842302
+ (x * (0.662328840472003 + (x * (-0.7122890234154284 + (x * (-0.05273963823400997
+ (x * (0.07952836873415717 + (x * (-0.0023339375937419 + (x * 0.0008862163904564247)))))))))))))))));
result := s1 / s2;
end;
function rational_p2q2(x : extended): extended;
var
s1, s2 : extended;
begin
if x = 0.0 then begin
result := -0.20243350835593876;
exit;
end;
s1 := -0.20243350835593876 + (x * (0.10526468069939171 + (x * (8.3705032834312
+ (x * (17.644729840837403 + (x * (-18.851064805871424 + (x * (-44.6382324441787
+ (x * (17.445385985570866 + (x * (21.12946554483405 + (x * -3.6719225470772936)))))))))))))));
s2 := 1.0 + (x * (6.242641248542475 + (x * (3.971343795334387 + (x * (-28.66081804998
+ (x * (-20.14326346804852 + (x * (48.560921310873994 + (x * (10.826866735546016
+ (x * (-22.643693341313973 + (x * 1.7211476576120028)))))))))))))));
result := s1 / s2;
end;
function rational_p3q3(x : extended): extended;
var
ax, ix, s1, s2 : extended;
begin
if x = 0.0 then begin
result := -0.1311027816799519;
exit;
end;
ax := abs(x);
if ax <= 1.0 then begin
s1 := -0.1311027816799519 + (x * (-0.16379404719331705 + (x * (0.11703015634199525
+ (x * (0.38707973897260434 + (x * (0.3377855389120359 + (x * (0.14286953440815717
+ (x * (0.029015791000532906 + (x * (0.0021455899538880526 + (x * (-6.794655751811263e-7
+ (x * (2.8522533178221704e-8 + (x * -6.81149956853777e-10)))))))))))))))))));
s2 := 1.0 + (x * (3.4662540724256723 + (x * (5.381683457070069 + (x * (4.778465929458438
+ (x * (2.5930192162362027 + (x * (0.848854343457902 + (x * (0.15226433829533179
+ (x * (0.011059242293464892 + (x * (0.0 + (x * (0.0 + (x * 0.0)))))))))))))))))));
end
else begin
ix := 1.0 / x;
s1 := -6.81149956853777e-10 + (ix * (2.8522533178221704e-8 + (ix * (-6.794655751811263e-7
+ (ix * (0.0021455899538880526 + (ix * (0.029015791000532906 + (ix * (0.14286953440815717
+ (ix * (0.3377855389120359 + (ix * (0.38707973897260434 + (ix * (0.11703015634199525
+ (ix * (-0.16379404719331705 + (ix * -0.1311027816799519)))))))))))))))))));
s2 := 0.0 + (ix * (0.0 + (ix * (0.0 + (ix * (0.011059242293464892 + (ix * (0.15226433829533179
+ (ix * (0.848854343457902 + (ix * (2.5930192162362027 + (ix * (4.778465929458438
+ (ix * (5.381683457070069 + (ix * (3.4662540724256723 + (ix * 1.0)))))))))))))))))));
end;
result := s1 / s2;
end;
function rational_p4q4(x : extended): extended;
var
ax, ix, s1, s2 : extended;
begin
if x = 0.0 then begin
result := -0.0350353787183178;
exit;
end;
ax := abs(x);
if ax <= 1.0 then begin
s1 := -0.0350353787183178 + (x * (-0.0022242652921344794 + (x * (0.018557330651423107
+ (x * (0.009508047013259196 + (x * (0.0018712349281955923 + (x * (0.00015754461742496055
+ (x * (0.00000460469890584318 + (x * (-2.304047769118826e-10 + (x * 2.6633922742578204e-12)))))))))))))));
s2 := 1.0 + (x * (1.3653349817554064 + (x * (0.7620591645536234 + (x * (0.22009110576413124
+ (x * (0.03415891436709477 + (x * (0.00263861676657016 + (x * (0.00007646752923027944
+ (x * (0.0 + (x * 0.0)))))))))))))));
end
else begin
ix := 1.0 / x;
s1 := 2.6633922742578204e-12 + (ix * (-2.304047769118826e-10 + (ix * (0.00000460469890584318
+ (ix * (0.00015754461742496055 + (ix * (0.0018712349281955923 + (ix * (0.009508047013259196
+ (ix * (0.018557330651423107 + (ix * (-0.0022242652921344794 + (ix * -0.0350353787183178)))))))))))))));
s2 := 0.0 + (ix * (0.0 + (ix * (0.00007646752923027944 + (ix * (0.00263861676657016
+ (ix * (0.03415891436709477 + (ix * (0.22009110576413124 + (ix * (0.7620591645536234
+ (ix * (1.3653349817554064 + (ix * 1.0)))))))))))))));
end;
result := s1 / s2;
end;
function rational_p5q5(x : extended): extended;
var
ax, ix, s1, s2 : extended;
begin
if x = 0.0 then begin
result := -0.016743100507663373;
exit;
end;
ax := abs(x);
if ax <= 1.0 then begin
s1 := -0.016743100507663373 + (x * (-0.0011295143874558028 + (x * (0.001056288621524929
+ (x * (0.00020938631748758808 + (x * (0.000014962478375834237 + (x * (4.4969678992770644e-7
+ (x * (4.625961635228786e-9 + (x * (-2.811287356288318e-14 + (x * 9.905570997331033e-17)))))))))))))));
s2 := 1.0 + (x * (0.5914293448864175 + (x * (0.1381518657490833 + (x * (0.016074608709367652
+ (x * (0.0009640118070051656 + (x * (0.000027533547476472603 + (x * (2.82243172016108e-7
+ (x * (0.0 + (x * 0.0)))))))))))))));
end
else begin
ix := 1.0 / x;
s1 := 9.905570997331033e-17 + (ix * (-2.811287356288318e-14 + (ix * (4.625961635228786e-9
+ (ix * (4.4969678992770644e-7 + (ix * (0.000014962478375834237 + (ix * (0.00020938631748758808
+ (ix * (0.001056288621524929 + (ix * (-0.0011295143874558028 + (ix * -0.016743100507663373)))))))))))))));
s2 := 0.0 + (ix * (0.0 + (ix * (2.82243172016108e-7 + (ix * (0.000027533547476472603
+ (ix * (0.0009640118070051656 + (ix * (0.016074608709367652 + (ix * (0.1381518657490833
+ (ix * (0.5914293448864175 + (ix * 1.0)))))))))))))));
end;
result := s1 / s2;
end;
begin
if (x < -1) or (x > 1) then begin
result := 0;
exit;
end;
if x = 1.0 then begin
result := infinity;
exit;
end;
if x = -1.0 then begin
result := - infinity;
exit;
end;
if x = 0.0 then begin
result := x;
exit;
end;
if x < 0.0 then sign := -1.0
else sign := 1.0;
ax := abs(x);
// |x| <= 0.5
if ax <= 0.5 then begin
g := ax * (ax + 10.0);
r := rational_p1q1(ax);
result := sign * ((g * Y1) + (g * r));
exit;
end;
q := 1.0 - ax;
// 1-|x| >= 0.25
if q >= 0.25 then begin
g := sqrt(-2.0 * ln(q));
q := q - 0.25;
r := rational_p2q2(q);
result := sign * (g / (Y2 + r));
exit;
end;
q := sqrt(-ln(q));
// q < 3
if q < 3.0 then begin
qs := q - 1.125;
r := rational_p3q3(qs);
result := sign * ((Y3 * q) + (r * q));
exit;
end;
// 3 =< q < 6
if q < 6.0 then begin
qs := q - 3.0;
r := rational_p4q4(qs);
result := sign * ((Y4 * q) + (r * q));
exit;
end;
// 6 =< q < 18
qs := q - 6.0;
r := rational_p5q5( qs );
result := sign * ((Y5* q) + (r * q ));
end;
//------------------------------------------------------------------------------
// C++ ライブラリより変換
// 元は Long double
function Inverse_error_double(x : extended): extended;
var
Ln2 : extended;
A : array[0..7] of extended;
B : array[0..7] of extended;
C : array[0..7] of extended;
D : array[0..7] of extended;
E : array[0..7] of extended;
F : array[0..7] of extended;
abs_x, r, num, den : extended;
i : integer;
begin
if (x < -1) or (x > 1) then begin
result := 0;
exit;
end;
if (x = -1) then begin
result := -INFiNITY;
exit;
end;
if (x = 1) then begin
result := INFiNITY;
exit;
end;
Ln2 := 6.931471805599453094172321214581e-1; // ln(2)
A[0] := 1.1975323115670912564578e0;
A[1] := 4.7072688112383978012285e1;
A[2] := 6.9706266534389598238465e2;
A[3] := 4.8548868893843886794648e3;
A[4] := 1.6235862515167575384252e4;
A[5] := 2.3782041382114385731252e4;
A[6] := 1.1819493347062294404278e4;
A[7] := 8.8709406962545514830200e2;
B[0] := 1.0000000000000000000e0;
B[1] := 4.2313330701600911252e1;
B[2] := 6.8718700749205790830e2;
B[3] := 5.3941960214247511077e3;
B[4] := 2.1213794301586595867e4;
B[5] := 3.9307895800092710610e4;
B[6] := 2.8729085735721942674e4;
B[7] := 5.2264952788528545610e3;
C[0] := 1.42343711074968357734e0;
C[1] := 4.63033784615654529590e0;
C[2] := 5.76949722146069140550e0;
C[3] := 3.64784832476320460504e0;
C[4] := 1.27045825245236838258e0;
C[5] := 2.41780725177450611770e-1;
C[6] := 2.27238449892691845833e-2;
C[7] := 7.74545014278341407640e-4;
D[0] := 1.4142135623730950488016887e0;
D[1] := 2.9036514445419946173133295e0;
D[2] := 2.3707661626024532365971225e0;
D[3] := 9.7547832001787427186894837e-1;
D[4] := 2.0945065210512749128288442e-1;
D[5] := 2.1494160384252876777097297e-2;
D[6] := 7.7441459065157709165577218e-4;
D[7] := 1.4859850019840355905497876e-9;
E[0] := 6.65790464350110377720e0;
E[1] := 5.46378491116411436990e0;
E[2] := 1.78482653991729133580e0;
E[3] := 2.96560571828504891230e-1;
E[4] := 2.65321895265761230930e-2;
E[5] := 1.24266094738807843860e-3;
E[6] := 2.71155556874348757815e-5;
E[7] := 2.01033439929228813265e-7;
F[0] := 1.414213562373095048801689e0;
F[1] := 8.482908416595164588112026e-1;
F[2] := 1.936480946950659106176712e-1;
F[3] := 2.103693768272068968719679e-2;
F[4] := 1.112800997078859844711555e-3;
F[5] := 2.611088405080593625138020e-5;
F[6] := 2.010321207683943062279931e-7;
F[7] := 2.891024605872965461538222e-15;
abs_x := abs(x);
if abs_x < 0.85 then begin
r := 0.180625 - 0.25 * x * x;
num := A[7];
den := B[7];
for i := 6 downto 0 do begin
num := num * r + A[i];
den := den * r + B[i];
end;
result := x * num / den;
exit;
end;
r := Sqrt(Ln2 - Ln(1.0 - abs_x));
if r <= 5.0 then begin
r := r - 1.6;
num := C[7];
den := D[7];
for i := 6 downto 0 do begin
num := num * r + C[i];
den := den * r + D[i];
end;
end
else begin
r := r - 5.0;
num := E[7];
den := F[7];
for i := 6 downto 0 do begin
num := num * r + E[i];
den := den * r + F[i];
end;
end;
result := num / den;
if x < 0 then
result := - result;
end;
//------------------------------------------------------------------------------
// '0.9999999999999999' '9'の値が長くなると正しく1に変換されません。
// 1.000000000000000222044604925031になる
// 一度stringに戻して再変換して切り捨てます。
// Doubleの演算では、値が1に近づくと演算制度が4桁程度迄落ちます。
// Double 5.0 * 10^-324 ~ 1.7 * 10^308 15~16桁
// Extended 3.6 * 10^-4951 ~ 1.1 * 10^4932 19~20桁
procedure TForm1.CalcBtnClick(Sender: TObject);
var
y, ans : bigdecimal;
yd, ansd : extended;
n : integer;
exstr : string;
{$IFDEF CPUX86} // プラットフォーム32ビット
L : integer;
{$ENDIF CPUX86}
begin
memo1.Clear;
//----------------------------------------------------------------------------
val(yedit.Text, yd, n);
if n <> 0 then begin
application.MessageBox('yの値に間違いがあります。','注意', 0);
exit;
end;
{$IFDEF CPUX64} // プラットフォーム64ビット
Memo1.Lines.Add('X64モード');
yd := strtofloat(floatTostr(yd)); // 0.9999999999999999 =>'1'-> 1
exstr := ' Double 8byte 演算';
{$ENDIF CPUX64}
{$IFDEF CPUX86} // プラットフォーム32ビット
Memo1.Lines.Add('X86モード');
L := length(yedit.Text);
if L > 30 then yd := strtofloat(Formatfloat('#0.########################',yd)); // 0.9999999999999999 =>'1'-> 1
exstr := ' Extended 10byte 演算';
{$ENDIF CPUX86}
// memo1.Lines.Append(floatTostr(yd - 1)); // 2.22044604925031E-16
if (-1 > yd) or (yd > 1) then begin
application.MessageBox('yの値が範囲外です。','注意', 0);
exit;
end;
//----------------------------------------------------------------------------
ansd := Inverse_error_double(yd);
memo1.Lines.Append('inverse error function');
memo1.Lines.Append('C++から変換' + exstr);
memo1.Lines.Append(' erfinv = ' + Formatfloat('#0.########################', ansd));
memo1.Lines.Append(' erfinv = ' + floatTostr(ansd));
//----------------------------------------------------------------------------
ansd := inverse_error_js(yd);
memo1.Lines.Append('');
memo1.Lines.Append('jsから変換' + exstr);
memo1.Lines.Append(' erfinv = ' + Formatfloat('#0.########################', ansd));
memo1.Lines.Append(' erfinv = ' + floatTostr(ansd));
//----------------------------------------------------------------------------
memo1.Lines.Append('');
memo1.Lines.Append('C++ から変換 多倍長演算');
y := yedit.Text;
ans := Inverse_error_long_double(y, n);
if n = 1 then
memo1.Lines.Append(' erfinv = INFINITY');
if n = -1 then
memo1.Lines.Append(' erfinv = -INFINITY');
if n = 0 then begin
ans := ans.RoundToPrecision(18); // 18桁丸め
if ans = 0 then
memo1.Lines.Append(' erfinv = 0.0')
else
memo1.Lines.Append(' erfinv = ' + ans.ToString);
end;
end;
procedure TForm1.erfBtnClick(Sender: TObject);
var
z, ans : Extended;
ch : integer;
exstr : string;
{$IFDEF CPUX86} // プラットフォーム32ビット
L : integer;
{$ENDIF CPUX86}
begin
memo1.Clear;
//----------------------------------------------------------------------------
val(zedit.Text, z, ch);
if ch <> 0 then begin
application.MessageBox('zの値に間違いがあります。','注意', 0);
exit;
end;
{$IFDEF CPUX64} // プラットフォーム64ビット
Memo1.Lines.Add('X64モード');
z := strtofloat(floatTostr(z)); // 0.9999999999999999 =>'1'-> 1
exstr := ' Double 8byte 演算';
{$ENDIF CPUX64}
{$IFDEF CPUX86} // プラットフォーム32ビット
Memo1.Lines.Add('X86モード');
L := length(zedit.Text);
if L > 30 then z := strtofloat(Formatfloat('#0.########################', z)); // 0.9999999999999999 =>'1'-> 1
exstr := ' Extended 10byte 演算';
{$ENDIF CPUX86}
memo1.Lines.Append('error function');
ans := Error_function(z);
memo1.Lines.Append(exstr);
memo1.Lines.Append(' erf = ' + floatTostr(ans));
end;
procedure TForm1.FormCreate(Sender: TObject);
var
tmp : extended;
begin
epsilon := 1;
repeat
epsilon := epsilon / 2;
tmp := 1 - epsilon;
until tmp = 1;
epsilon := epsilon * 2;
bigdecimal.DefaultPrecision := DPS;
end;
end.
erf.pas
unit erf; interface function Error_function(z : Extended): Extended; implementation uses system.Math, system.SysUtils, main; // erf(z) function Error_function(z : Extended): Extended; var mzh2, zhn, s, sb, tmp, zmax : Extended; pai2 : Extended; n, nl, nn : Extended; begin {$IFDEF CPUX64} // プラットフォーム64ビット zmax := 4; {$ENDIF CPUX64} {$IFDEF CPUX86} // プラットフォーム64ビット zmax := 4.7; {$ENDIF CPUX86} if abs(z) > zmax then begin if z >= 0 then result := 1 else result := -1; exit; end; pai2 := 2.0 / Sqrt(pi); // 2/√(π) mzh2 := -z * z; // -z^2 s := z; // n = 0時 z nl := 1.0; // 0! = 1 zhn := z; // n = 0時 z n := 1.0; // n=1から repeat sb := s; nn := n + n + 1.0; // 2n+1 nn := nn * nl; // n!(2n+1) zhn := zhn * mzh2; // ((-1)^n)(z^(2n+1)) tmp := zhn / nn; // ((-1)^n)(z^(2n+1))/(n!(2n+1)) s := s + tmp; // Σ+Δ n := n + 1.0; // inc(n) nl := nl * n; // n! until (sb = s) or (abs(tmp) <= epsilon); result := s * pai2; // Σ* 2/√(π) if abs(result) >=1 then if result >=0 then result := 1.0 else result := -1.0; form1.Memo1.Lines.Append(' loops= ' + floatTostr(n)); end; end.
![]() inverse_error_function.zip
inverse_error_function.zip
三角関数、逆三角関数、その他関数 に戻る