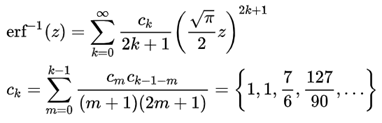
c0=1
逆誤差関数(Inverse error functtion)
名前の通り、誤差関数値から元の値を値を求めるものです。
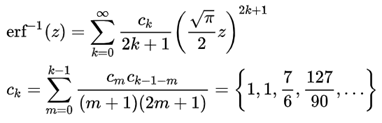
c0=1
上記の計算で、問題になるのは、 Ckの値で、この計算は、kの値が大きくなるにつれて、計算量が非常に多くなります。
誤差関数の値は-1～1なのですが、誤差関数 0.999の値を求めようとすると、ｋの最大値は、100000となってしまいます。
Ｃkの値が既知ならば問題ないのですが、配列を用意して100000迄計算すると、此処のプログラムでは半日以上掛かります。
一度計算をしておいて、ファイルに保存しておけば読みだして再利用が可能です。
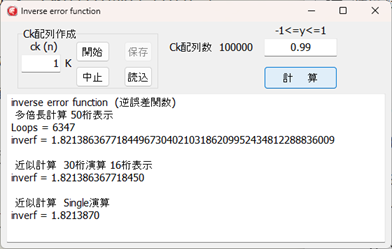Ckの配列は、プログラムの起動時1000個を作成します。
しかし1000個では、y=0.937迄しか対応できません。
Ckの配列を半日かけて100000個分作成しても対応出来るのはy=0.999375迄です。
現実には、それほど、有効桁数を必要としないと思われるので、c++のerfinv計算を移植してみました。
C++では、Long Double
で10byte演算だったのですが、現在は64ビットモードだと8byte演算Doubleで計算されるので、演算精度が不足します。
そこで、多倍長演算をして、表示16桁にしてみました。
16桁正しく演算されます。
0～0.9999999999999999999999999999999999999999999999999999999999999999999999999999
の範囲でテストをしてみましたが、16桁正しい値を返します。
Doubleで計算すると、15桁の精度となりｙの値が0.9999を超えた辺りから多少の誤差が出るようです。
此処のプログラムには組み込んでありませんが、x86モードの10byte精度(extended)で 0.9999999迄は正しい答えを返します。
参考に演算精度が数桁で良いのならとsingleでのプログラムも変換してみました。
これは、完全に4byte演算です。
プログラム
Biginteger & Bigdecimal の組み込み方は第１種ケルビン関数を参照して下さい。
// Inverse Error function // Ck値によるinvErfの計算の場合、Ckの配列をかなり大きくしても、0.999・・・の値の場合配列の数が不足します。 // プログラムでは1000k(100万)迄作成出来るようにしてありますが100k迄しかテストしていません。 // 100kの作成で、PCにもよりますが10時間程度必要とします。1000k作成すると日単位となって現実的でありません。 // 100kで0.99937程度までは50桁の答えが計算できます。 // プログラム起動時は1kに設定してあります。 // 精度と必要性から考えると、近似計算の16桁の精度計算で良いようにおもわれます。 // 近似計算の場合0.99・・・50桁以上でも問題なく計算できます。 // 近似計算はc言語のerfinv関数をdelphi bigdecimal用に変換したものです。 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, system.UITypes; type TForm1 = class(TForm) CalcBtn: TButton; Memo1: TMemo; yEdit: TLabeledEdit; GroupBox1: TGroupBox; CkEdit: TLabeledEdit; Label1: TLabel; mbtn: TButton; cbtn: TButton; sbtn: TButton; rbtn: TButton; SaveDialog1: TSaveDialog; OpenDialog1: TOpenDialog; MaxloopsLabel: TLabel; procedure CalcBtnClick(Sender: TObject); procedure mbtnClick(Sender: TObject); procedure cbtnClick(Sender: TObject); procedure sbtnClick(Sender: TObject); procedure rbtnClick(Sender: TObject); private { Private 宣言 } public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses system.Math, Velthuis.BigIntegers, Velthuis.Bigdecimals; const DPS = 200; // 除算時有効桁数 EPS = '1e-60'; // 収束判定値デフォルト DPSCK = DPS div 2; var KMAX : integer; Kmaxm : integer; Cka : array of bigdecimal; Ckm : array of bigdecimal; BR : boolean; F1 : textFile; //--------------------------------- Ln(x)--------------------------------------- // x = m * 2^n のnの値と2^nの値を戻します // result = n // ta = 2^n // m = x / 2^n function frexpa(x: bigdecimal; var ta: biginteger): integer; var tb: biginteger; xi, one: bigdecimal; n, j, s, pcs : integer; begin pcs := BigDecimal.DefaultPrecision; one := '1'; one := one.RoundToPrecision(pcs); xi := x; // x保存 if xi < one then x := one / x; // 1より小さかったら逆数 ta := '1'; n := 0; j := 0; // シフト回数クリア ta := '1'; // ta初期値 s := 4096; // s=4^i i = 6 repeat while x > ta do begin biginteger.ShiftLeft(ta, s, tb); // s分左シフト ta := tb; inc(j); // シフト回数インクリメント end; if (s > 1) and (j > 0) then begin // ta > x になったら dec(j); // シフト回数デクリメント biginteger.Shiftright(ta, s, tb); // s分右シフト ta := tb; end; n := n + s * j; // 2^nのn計算 j := 0; // シフト回数クリア s := s shr 2; // sの値を1/4にする 右へ2ビットシフト // s := s div 4; // sの値を1/4にする until s = 0; // s= ...16, 4, 1, 0 if xi < one then begin // より小さかったら n := -n + 1; // 2^nのn値負数 biginteger.Shiftright(ta, 1, tb); // 上式+1により右シフト ta := tb; end; result := n // ta = 2^n end; // 小さい値のlog計算 // xi 実数 // dpcs 有効桁数 // ans log値 // 戻り値 Loopオーバーフロー 無し true 有り false // loop制限の無い場合 1e-4～1e4 が計算出来る範囲 // loop制限 5.8e-3 ～1.73e2 (kk=10000の場合) function Log_11(x: bigdecimal; dpcs: integer; var ans: bigdecimal): boolean; const KK = 10000; var one, two, x1, x2, i, s, last: bigdecimal; k : integer; begin result := true; one := '1'; two := '2'; x1 := (x - one) / (x + one); // x1 = (x-1)/(x+1) x2 := x1 * x1; // x1^2 x2 := x2.RoundToPrecision(dpcs); i := one; // i=1 s := x1; // s初期値 k := 0; // 長ループ脱出用カウンタ0 repeat x1 := x1 * x2; // x1^2n+1 x1 := x1.RoundToPrecision(dpcs); i := i + two; // 2n+1 i := i.RoundToPrecision(dpcs); last := s; // 判定用sの値保存 s := s + x1 / i; // Σs = s + x1^2n+1 / (2n+1) s := s.RoundToPrecision(dpcs); // 収束判定の為指定有効桁数以下丸め inc(k); // ループカウンタインクリメント until (last = s) or (k > KK); // 収束判定 ans := two * s; if k > kk then result := false; end; // loge(x) ln(x) // 級数展開 // 1e±500000 程度が限度 // sm <xi< last の範囲外の場合 (0.7～xi～1.4) * 2^nに変換 xiが1に近いほど変換早い function log_bigf(xi: bigdecimal): bigdecimal; label EXT; const KK = 10000; var LOG2, SQRT2, two, last, s, sm, one, one1, k2, a: bigdecimal; k : integer; kb, ta : biginteger; pcsBack, dpcs : integer; rmback : BigDecimal.RoundingMode; begin result := '0'; if xi <= result then begin application.MessageBox('無効な値です。','注意',0); exit; end; sm := '1e-2'; last := '5e1'; pcsBack := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ dpcs := pcsBack + 5; // 指定精度 + α BigDecimal.DefaultPrecision := dpcs; BigDecimal.DefaultRoundingMode := rmNearesteven; one := '1'; if xi = one then begin goto EXT; end; if (xi > sm) and (xi < last) then begin // 0.01 < xi < 50の時はLog11計算 if Log_11(xi, dpcs, a) then begin // log11 result := a; goto EXT; end; end; one1 := '1e500000'; if xi < one then begin // xi < 1 last := one / xi; // 1 / xi if last > one1 then begin // (1 / xi) > 1e500000 application.MessageBox('値が小さすぎます。','注意',0); goto EXT; end; end; if xi > one1 then begin // xi > 1e500000 application.MessageBox('値が大きすぎます。','注意',0); goto EXT; end; xi := xi.RoundToPrecision(dpcs); two := '2'; Log_11(two, dpcs, LOG2); // log(2) SQRT2 := bigdecimal.Sqrt(two, dpcs * 2); // √2 k := frexpa(xi / SQRT2, ta); // x / √2 = m * 2^k ta = 2^k kb := k; k2 := ta; // 2^k integer to decimal k2 := k2.RoundToPrecision(dpcs); if k < 0 then begin // kが負数だったら xi := xi * k2; // x * 2^k x=0.707～1.414 √2 xi := xi.RoundToPrecision(dpcs); end else begin xi := xi / k2; // x / 2^k x=0.707～1.414 √2 end; if xi <> one then begin // xi <> 1 なら Log_11(xi, dpcs, s) // log(xi) end else s := '0'; // xi=1なら s=0 result := LOG2 * kb + s; EXT: result := result.RoundToPrecision(pcsBack); BigDecimal.DefaultPrecision := pcsBack; // 除算演算精度復帰 BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰 end; // log(x) function log_big(xi: bigdecimal): bigdecimal; begin result := log_bigf(xi); end; //----------------------------- errinv 10byte相当------------------------------- // Cライブラリより変換 // 元は LongDouble 10byte演算でしたがwin11では無いため多倍長演算を使用 // 演算結果の表示時に16桁に丸めます。 // 近似計算用データーは20桁ありますが、誤差により16桁程度の精度となります。 // doubleでの計算でも15桁程度の精度は出ますが1に近い0.9999999999999999の場合無限大になります。 function Inverse_error_long_double(x : bigdecimal; var INF : integer): bigdecimal; const DPSLD = 30; var LN2 : bigdecimal; A : array[0..7] of bigdecimal; B : array[0..7] of bigdecimal; C : array[0..7] of bigdecimal; D : array[0..7] of bigdecimal; E : array[0..7] of bigdecimal; F : array[0..7] of bigdecimal; abs_x, r, num, den : bigdecimal; d1, d2 : bigdecimal; i : integer; begin INF := 0; if (x < -1) or (x > 1) then begin result := 0; exit; end; if (x = -1) then begin INF := - 1; exit; end; if (x = 1) then begin INF := 1; exit; end; bigdecimal.DefaultPrecision := DPSLD; // 除算30桁設定 LN2 := '6.931471805599453094172321214581e-1'; A[0] := '1.1975323115670912564578e0'; A[1] := '4.7072688112383978012285e1'; A[2] := '6.9706266534389598238465e2'; A[3] := '4.8548868893843886794648e3'; A[4] := '1.6235862515167575384252e4'; A[5] := '2.3782041382114385731252e4'; A[6] := '1.1819493347062294404278e4'; A[7] := '8.8709406962545514830200e2'; B[0] := '1.0000000000000000000e0'; B[1] := '4.2313330701600911252e1'; B[2] := '6.8718700749205790830e2'; B[3] := '5.3941960214247511077e3'; B[4] := '2.1213794301586595867e4'; B[5] := '3.9307895800092710610e4'; B[6] := '2.8729085735721942674e4'; B[7] := '5.2264952788528545610e3'; C[0] := '1.42343711074968357734e0'; C[1] := '4.63033784615654529590e0'; C[2] := '5.76949722146069140550e0'; C[3] := '3.64784832476320460504e0'; C[4] := '1.27045825245236838258e0'; C[5] := '2.41780725177450611770e-1'; C[6] := '2.27238449892691845833e-2'; C[7] := '7.74545014278341407640e-4'; D[0] := '1.4142135623730950488016887e0'; D[1] := '2.9036514445419946173133295e0'; D[2] := '2.3707661626024532365971225e0'; D[3] := '9.7547832001787427186894837e-1'; D[4] := '2.0945065210512749128288442e-1'; D[5] := '2.1494160384252876777097297e-2'; D[6] := '7.7441459065157709165577218e-4'; D[7] := '1.4859850019840355905497876e-9'; E[0] := '6.65790464350110377720e0'; E[1] := '5.46378491116411436990e0'; E[2] := '1.78482653991729133580e0'; E[3] := '2.96560571828504891230e-1'; E[4] := '2.65321895265761230930e-2'; E[5] := '1.24266094738807843860e-3'; E[6] := '2.71155556874348757815e-5'; E[7] := '2.01033439929228813265e-7'; F[0] := '1.414213562373095048801689e0'; F[1] := '8.482908416595164588112026e-1'; F[2] := '1.936480946950659106176712e-1'; F[3] := '2.103693768272068968719679e-2'; F[4] := '1.112800997078859844711555e-3'; F[5] := '2.611088405080593625138020e-5'; F[6] := '2.010321207683943062279931e-7'; F[7] := '2.891024605872965461538222e-15'; abs_x := x.Abs(x); if abs_x < '0.85' then begin d1 := '0.180625'; d2 := '0.25'; r := d1 - d2 * x * x; num := A[7]; den := B[7]; for i := 6 downto 0 do begin num := num * r + A[i]; den := den * r + B[i]; end; num := num.RoundToPrecision(DPSLD); den := den.RoundToPrecision(DPSLD); result := x * num / den; bigdecimal.DefaultPrecision := DPS; // 除算有効桁数元に戻し exit; end; r := bigdecimal.Sqrt(LN2 - log_big(bigdecimal.One - abs_x), DPSLD + DPSLD); if r <= '5.0' then begin d1 := '1.6'; r := r - d1; num := C[7]; den := D[7]; for i := 6 downto 0 do begin num := num * r + C[i]; den := den * r + D[i]; end; end else begin d2 := '5.0'; r := r - d2; num := E[7]; den := F[7]; for i := 6 downto 0 do begin num := num * r + E[i]; den := den * r + F[i]; end; end; num := num.RoundToPrecision(DPSLD); den := den.RoundToPrecision(DPSLD); result := num / den; if x < '0' then result := - result; bigdecimal.DefaultPrecision := DPS; // 除算有効桁数元に戻し end; //------------------------------------- π-------------------------------------- // π // https://www.kurims.kyoto-u.ac.jp/~ooura/pi_fft-j.html // T.Ooura AGM アルゴリズ function pi_big: Bigdecimal; var n, dpcs : integer; rmback : BigDecimal.RoundingMode; SQRT_SQRT_EPSILON, c, b, e : BigDecimal; npow : Bigdecimal; a, one, two, four, five, eight : Bigdecimal; begin rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ dpcs := DPS + 5; // 指定精度 + α BigDecimal.DefaultPrecision := dpcs; BigDecimal.DefaultRoundingMode := rmNearesteven; one := '1'; one := one.RoundToPrecision(dpcs); // oneの有効桁数をdpcsに設定 two := '2'; four := '4'; five := '5'; eight := '8'; SQRT_SQRT_EPSILON := one / BigDecimal.IntPower(two, dpcs shl 0); // 収束判定値 c := BigDecimal.Sqrt(one / eight, dpcs * 2); a := one + c + c + c; b := BigDecimal.Sqrt(a, dpcs * 2); e := b - five / eight; b := b + b; c := e - c; a := a + e; npow := '4'; n := 0; while (e > SQRT_SQRT_EPSILON) and (n < 100) do begin npow := npow + npow; // 8,16,32,64 e := (a + b) / two; // 平均値 除算有効桁数での丸め b := a * b; b := b.RoundToPrecision(dpcs); // pcs + α 丸め b := BigDecimal.Sqrt(b, dpcs * 2); // 平方根有効桁数での丸め e := e - b; b := b + b; c := c - e; a := e + b; inc(n); end; e := e * e; e := e.RoundToPrecision(dpcs); // pcs + α 丸め e := e / four; // e = e * e / 4 a := a + b; result := (a * a - e - e / two) / (a * c - e) / npow; // 除算の順番に注意 result := result.RoundToPrecision(DPS); // 指定の精度に丸め BigDecimal.DefaultPrecision := DPS; // 除算演算精度復帰 BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰 end; //------------------------------------------------------------------------------ // 数値の後ろのゼロ消去 function ZeroErase(s : string): string; const EP = 'e'; ZC = '0'; DT = '.'; var c : char; i, j, k, l : integer; begin l := length(s); j := 1; for i := 1 to l do begin c := s[i]; if c = EP then begin j := i - 1; break; end; j := i; end; result := ''; if j < l then begin for i := l downto j + 1 do result := s[i] + result; end; K := 1; for i := j downto 1 do begin c := s[i]; if c <> ZC then begin k := i; if c = DT then k := k + 1; break; end; end; for i := k downto 1 do result := s[i] + result; end; //-----------------------------Ck[n]配列初期値計算------------------------------ // プログラム起動時Ck[n]の計算 procedure ck(k : integer); var j : integer; top, Bottom : bigdecimal; one, mb, s : bigdecimal; procedure ckcalc(k : integer); var m : integer; begin one := '1'; Cka[0] := one; mb := bigdecimal.Zero; s := 0; for m := 0 to k - 1 do begin Bottom := (mb + one) * (mb + mb + one); // 分母 top := CKa[m] * Cka[k - m - 1]; // 分子 bottom := bottom.RoundToPrecision(DPS); top := top.RoundToPrecision(DPS); s := s + top / bottom; // Σ mb := mb + one; end; s := s.RoundToPrecision(DPSCK); if k > 0 then cka[k] := s; end; begin for j := 0 to k do ckcalc(j); // Ck(0)～Ck(k)計算 end; //---------------------------------erfinv--------------------------------------------- // InvErfのCk配列による計算 function Inverse_error(y: bigdecimal; var k : integer): bigdecimal; var kb, s, pai, one, two, aks2k1, sd, abssd : bigdecimal; rps2y, rps2yh2 : bigdecimal; k2p1: bigdecimal; begin one := bigdecimal.One; two := one + one; // 2 pai := pi_big; // π pai := pai.Sqrt(pai, DPS + DPS); // √(π) rps2y := pai / two * y; // √(π)/2 * y rps2yh2 := rps2y * rps2y; s := 0; k := 0; kb := bigdecimal.Zero; repeat k2p1 := kb + kb + one; aks2k1 := CKa[k] / k2p1; sd := rps2y * aks2k1; s := s + sd; kb := kb + one; rps2y := rps2y * rps2yh2; rps2y := rps2y.RoundToPrecision(DPS); inc(k); abssd := sd.Abs(sd); until (abssd < EPS) or (k > KMAX); result := s; form1.Memo1.Lines.Append('Loops = ' + inttostr(k - 1)); end; //------------------------------ erfinv single --------------------------------------- function erfinv_single(x : single): single; var w, p: single; begin if abs(x) = 1 then begin if x > 0 then result := infinity else result := -infinity; exit; end; w := - ln((1.0 - x) * (1.0+x)); if w < 5.0 then begin w := w - 2.5; p := 2.81022636e-08; p := 3.43273939e-07 + p * w; p := -3.5233877e-06 + p * w; p := -4.39150654e-06 + p * w; p := 0.00021858087 + p * w; p := -0.00125372503 + p * w; p := -0.00417768164 + p * w; p := 0.24664072 + p * w; p := 1.50140941 + p * w; end else begin w := sqrt(w) - 3.0; p := -0.000200214257; p := 0.000100950558 + p * w; p := 0.00134934322 + p * w; p := -0.00367342844 + p * w; p := 0.00573950773 + p * w; p := -0.0076224613 + p * w; p := 0.00943887047 + p * w; p := 1.00167406 + p * w; p := 2.83297682 + p * w; end; result := p * x; end; //---------------------------------- calc -------------------------------------- // 入力値によるInvErf計算 procedure TForm1.CalcBtnClick(Sender: TObject); var y, ans, absy : bigdecimal; yd, ansd : bigdecimal; n, INF : integer; sy, sans : single; begin if not mbtn.Enabled then exit; try y := yedit.Text; except on EConverterror do begin MessageDlg('y の値に間違いがあります。', mtError, [mbOK], 0); exit; end; end; absy := y.Abs(y); if absy > bigdecimal.One then begin MessageDlg('y の絶対値|y|は1又は1以下にしてください。', mtWarning, [mbOK], 0); exit; end; //------------------------------- 多倍長 ------------------------------------- calcBtn.Enabled := false; memo1.Clear; memo1.Lines.Append('inverse error function (逆誤差関数)'); memo1.Lines.Append(' 多倍長計算 50桁表示'); if absy < bigdecimal.One then begin ans := Inverse_error(y, n); // Ck配列によるInvErfの計算 if n > KMAX then memo1.Lines.Append('Ck配列の最大値を超えました答えは正しくありません。'); ans := ans.RoundToPrecision(50); if ans = '0' then memo1.Lines.Append('inverf = 0.0') else memo1.Lines.Append('inverf = ' + ZeroErase(ans.ToString)); end else begin Memo1.Lines.Append('Loops = 0'); if y > 0 then memo1.Lines.Append('inverf = ∞') else memo1.Lines.Append('inverf = -∞'); end; //-------------------- 近似計算 多倍長 30桁 ---------------------------------- memo1.Lines.Append(''); memo1.Lines.Append(' 近似計算 30桁演算 16桁表示'); yd := yedit.Text; ansd := Inverse_error_long_double(yd, INF); // 近似値によるInvErfの計算 if INF = 0 then begin ansd := ansd.RoundToPrecision(16); if ans = '0' then memo1.Lines.Append('inverf = 0.0') else memo1.Lines.Append('inverf = ' + ansd.ToString); end else begin if INF = 1 then Memo1.Lines.Append('INF'); if INF = -1 then Memo1.Lines.Append('-INF'); end; //-------------------- 近似計算 single 演算 --------------------------------- memo1.Lines.Append(''); memo1.Lines.Append(' 近似計算 Single演算'); sy := strtofloat(yedit.Text); sans := erfinv_single(sy); memo1.Text := memo1.Text + 'inverf = ' + floatTostrF(sans, ffFixed, 7, 7); calcBtn.Enabled := true; end; //---------------------------- Ck[n]配列のファイル操作-------------------------- procedure CkmaxLoopsdisp(n: integer); begin Form1.MaxloopsLabel.Caption := 'Ck配列数 ' + intTostr(n); end; // Ck[n]の新規計算-------------------------------------------------------------- // Ck[n]の初期値設定と殆ど同じですが、デバッグの都合上別に設定 procedure ckb(k : integer); var j : integer; top, Bottom : bigdecimal; one, mb, s : bigdecimal; procedure ckcalc(k : integer); var m : integer; begin one := '1'; Ckm[0] := one; mb := bigdecimal.Zero; s := 0; for m := 0 to k - 1 do begin Bottom := (mb + one) * (mb + mb + one); // 分母 top := CKm[m] * Ckm[k - m - 1]; // 分子 bottom := bottom.RoundToPrecision(DPS); top := top.RoundToPrecision(DPS); s := s + top / bottom; // Σ mb := mb + one; end; s := s.RoundToPrecision(DPSCK); // 有効桁数DPSの1/2 if k > 0 then ckm[k] := s; end; begin for j := 0 to k do begin // j=0～k ckcalc(j); // ck(j)計算 if j mod 100 = 0 then begin // 100ループ一回 ループNo表示 form1.Memo1.Lines.Append(' Ck作成 loops = ' + inttostr(j)); end; application.ProcessMessages; if BR then break; // 中止入力でブレーク end; KMAXm := j - 1; // Ckの計算済み最大値 end; // 新規配列作成の中止 procedure TForm1.cbtnClick(Sender: TObject); begin BR := True; end; // Ck(n)の新規作成 procedure TForm1.mbtnClick(Sender: TObject); var ch, k : integer; begin if not calcbtn.Enabled then exit; val(ckEdit.Text, K, ch); if ch <> 0 then begin application.MessageBox('Ck(n)の値に間違いが在ります。','注意',0); exit; end; if K > 1000 then begin application.MessageBox('Ck(n)の値が大きすぎます1000K以下にしてください。','注意',0); exit; end; mbtn.Enabled := false; sbtn.Enabled := false; rbtn.Enabled := false; BR := False; KMAXm := k * 1000; setlength(Ckm, kMAXm + 1); // Ck(n)の長さ設定 ckb(KMAXm); // Ck(n)の新規計算 KMAX := kMAXm; // 配列の最大値Ck(m)の新規計算の最大値に変更 setlength(Cka, KMAX + 1); // invEnf計算用Cka配列の長さを設定 for k := 0 to KMAX do cka[k] := ckm[k]; // 配列のコピー memo1.Lines.Append('Ck(n)の作成完了しました。' + 'Ck(n) nMax= ' + intTostr(KMAXm)); CkmaxLoopsdisp(KMAX); mbtn.Enabled := true; sbtn.Enabled := true; rbtn.Enabled := true; end; // Ck[n]配列のファイルからの読み込み ------------------------------------------------- function dataread: integer; var i, Km : integer; L : string; begin result := 0; readln(f1, L); km := strtoint(L); setlength(ckm, km); for i := 0 to km do begin readln(f1, L); ckm[i] := L; end; result := km; end; procedure TForm1.rbtnClick(Sender: TObject); var i, km : integer; begin if OpenDialog1.Execute then begin if not FileExists(OpenDialog1.FileName) then exit; AssignFile(F1, OpenDialog1.FileName); reset(F1); end; try km := dataread; finally closeFile(F1); end; if km > 1000 then begin setlength(Cka, km); for i := 0 to km do Cka[i] := Ckm[i]; KMAX := km; CkmaxLoopsdisp(KMAX); end; end; // Ck[n]配列のファイルへの保存 ------------------------------------------------- procedure datawrite; var i : integer; begin Writeln(F1,inttostr(KMAX)); for i := 0 to KMAX do begin Writeln(F1, Cka[i].ToString); end; end; procedure TForm1.sbtnClick(Sender: TObject); var LLS : string; begin if SaveDialog1.Execute then begin LLS := ChangeFileExt(SaveDialog1.FileName,'.Ckd'); if FileExists(LLS) then if MessageDlg('既にファイルが存在します 上書きしますか',mtConfirmation, [mbYes, mbNo], 0) = mrNo then exit; AssignFile(F1,LLS); { ダイアログで選択されたファイル } ReWrite(F1); try datawrite; // 修正データー書き込み finally closeFile(F1); end; end; end; //------------------------------------------------------------------------------ // 初期値設定 initialization kMAX := 1000; bigdecimal.DefaultPrecision := DPS; setlength(Cka, KMAX + 1); ck(KMAX); end.
inverse_error_function_test.zip
三角関数、逆三角関数、その他関数 に戻る