非線形方程式の数値解法 続き
非線形方程式y=f(x)で、指定されたxの範囲の最小値(最下点)あるいは最大値(最上点)を求める計算です。
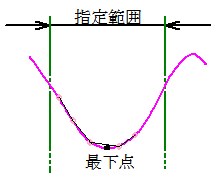微分が出来れば、変化がゼロになる点を求めれば簡単に計算が出来ますが、微分が容易でない場合二分法に近い方法で計算しますが、f(a)f(b)<0になる事は有りません。
この場合は、指定範囲の片方から指定のピッチで計算し、前の計算値と、新しい値の計算値の差分の符号が変化する場所を検出し、最小値(最下点)あるいは最大値(最高点)を求めます。
{f(a)-f(b)}{f(b)-f(c)] < 0 となる点です。
最初は、ある程度大きなピッチで計算し、符号がが反転したら、ピッチを二つ戻し、ピッチを小さくし再度計算することを繰り替えし、ピッチが指定値epsilon以下になったら、計算終了とします。
ピッチを二つ戻すのは、最小値(最下点)あるいは最大値(最高点)をピッチが過ぎても、差分の符号が反転しない場合があるからです、この場合は二つ過ぎたところで符号が反転します。
この手法は、ねじ歯車の軸間距離の計算に使用しています。
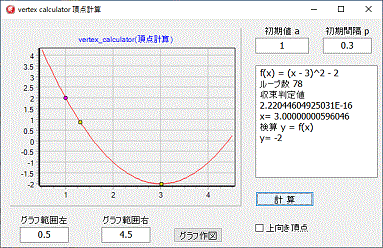
プログラム
プログラム、簡単に微分可能な計算式となっていますが、あくまでもプログラム例です。
// 非線形方程式の最大値(頂点)又は最小値(谷点)検出 // 最大値(頂点)のx軸方向の値は、誤差が大きくなります、最大値(頂点)は水平に成るためです。 // グラフを最初に作図して、範囲の確認をします。 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, VCLTee.Series, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) Chart1: TChart; Series1: TLineSeries; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; BitBtn1: TBitBtn; Memo1: TMemo; Series3: TPointSeries; Series4: TPointSeries; LabeledEdit3: TLabeledEdit; LabeledEdit4: TLabeledEdit; BitBtn2: TBitBtn; CheckBox1: TCheckBox; procedure BitBtn1Click(Sender: TObject); procedure BitBtn2Click(Sender: TObject); procedure LabeledEdit1Change(Sender: TObject); procedure LabeledEdit2Change(Sender: TObject); procedure LabeledEdit3Change(Sender: TObject); procedure LabeledEdit4Change(Sender: TObject); procedure CheckBox1Click(Sender: TObject); private { Private 宣言 } procedure chart_graph(gl, gr: double); public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} // 関数f(x)の計算式 非線形方程式 function f(x: double): double; begin result := (x - 3) * (x - 3) - 2; // result := x * x; if form1.CheckBox1.Checked = true then result := -result; end; // 区間[gl,gr]の関数f(x)のグラフを作図 procedure TForm1.chart_graph(gl, gr: double); const n = 100; var x, xs, xe, dx: double; y : double; i : integer; begin series1.clear; series3.clear; series4.clear; if gl = gr then exit; // 範囲がゼロだったら終了 xs := gl; xe := gr; dx := (xe - xs) / n; for i := 0 to n do begin x := xs + i * dx; y := f(x); series1.AddXY(x, y); end; end; // 頂点の近似値計算 function bisection_method(a, p, epsilon: double; var loop: integer): double; var fn, fa: double; chf : boolean; begin // 初期指定点とピッチ確認 fn := f(a); // 初期点計算 fa := f(a + p); chf := false; if form1.CheckBox1.Checked = true then begin if fn > fa then chf := true; // 上向き頂点 end else begin if fn < fa then chf := true; // 下向き頂点 最下点 end; if chf then begin result := 0; exit; end; // 頂点の計算 repeat chf := false; fa := fn; // 前の値 a := a + p; // 次の点 fn := f(a); // 次の点計算 if form1.CheckBox1.Checked = true then begin if fn < fa then chf := true; // 上向き頂点 end else begin if fn > fa then chf := true; // 下向き頂点 最下点 end; if chf then begin a := a - p - p; // 2ピッチ戻し p := p / 4; fn := f(a); // 元の値再計算 end; inc(loop); until (p < epsilon * (abs(a) + 1)) or (loop > 500); result := a; end; // 計算実行 procedure TForm1.BitBtn1Click(Sender: TObject); var a, p, alpha, y : double; loop : integer; epsilon, tmp : double; begin a := strTofloat(labelededit1.Text); p := strTofloat(labelededit2.Text); memo1.Clear; // 収束判定値計算 epsilon := 1; repeat epsilon := epsilon / 2; tmp := 1 + epsilon; until tmp = 1; epsilon := epsilon * 2; // 非線形方程式の計算 loop := 0; alpha := bisection_method(a, p, epsilon, loop); if loop = 0 then begin application.MessageBox('初期値の位置に間違いがある、又はピッチが大きすぎます。','注意',0); exit; end; // 検算 y := f(alpha); // 計算結果表示 series4.AddXY(alpha, y); memo1.Lines.Append('f(x) = (x - 3)^2 - 2'); memo1.Lines.Append('ループ数 ' + intTostr(loop)); memo1.Lines.Append('収束判定値'); memo1.Lines.Append(floatTostr(epsilon)); memo1.Lines.Append('x= ' +floatTostr(alpha)); memo1.Lines.Append('検算 y = f(x)'); memo1.Lines.Append('y= ' +floatTostr(y)); end; procedure TForm1.BitBtn2Click(Sender: TObject); var gl, gr : double; ch : integer; a, p, y : double; begin val(labelededit3.Text, gl, ch); if ch <> 0 then begin application.MessageBox('グラフ範囲左に間違いが有ります。','注意',0); exit; end; val(labelededit4.Text, gr, ch); if ch <> 0 then begin application.MessageBox('グラフ範囲右に間違いが有ります。','注意',0); exit; end; if gr <= gl then begin application.MessageBox('グラフ範囲右には左より大きくして下さい。','注意',0); exit; end; chart_graph(gl, gr); application.ProcessMessages; val(labelededit1.Text, a, ch); if ch <> 0 then begin application.MessageBox('初期値aに間違いが有ります。','注意',0); exit; end; val(labelededit2.Text, p, ch); if ch <> 0 then begin application.MessageBox('初期間隔pに間違いが有ります。','注意',0); exit; end; if (a < gl) or (a > gr) then begin application.MessageBox('初期値aがグラフの範囲外です。','注意',0); exit; end; if a > (gr - gl) / 2 + gl then begin application.MessageBox('初期値aは左寄りにして下さい。','注意',0); exit; end; y := f(a); series3.AddXY(a, y); application.ProcessMessages; if p > (gr - gl) / 2 then begin application.MessageBox('初期間隔pが大きすぎます。','注意',0); exit; end; if p <= 0 then begin application.MessageBox('初期間隔pはゼロより大きくして下さい。','注意',0); exit; end; y := f(a + p); series4.AddXY(a + p, y); application.ProcessMessages; bitbtn1.Enabled := True; end; procedure TForm1.LabeledEdit1Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit2Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit3Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit4Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.CheckBox1Click(Sender: TObject); begin bitbtn1.Enabled := false; end; end.
ギヤ(歯車)の計算の場合、計算の精度は千分の一以下であれば精度で実用上問題ないのでDoubleの精度でOKですが、大きな精度が必要な場合は、多倍長bigdecimalの計算が必要です。
bigdecimalの組み込みは、ベルヌーイ数その４をbig_mathについては、bigdecimalによるmathを参照してください。
Delphiの多倍長計算にはMPArithもあります、これを使用するのであれば、組み込み方は、ベルヌーイ数その２を参照してください。
MPArithははfunctioｎ形式が使用出来ない為、工夫が必要です。
bigdecimalによるプログラム
// 非線形方程式の最大値最小値検出 // 最大値最小値のx軸方向の値は、誤差が大きくなります、最大値最小値の近辺は水平に成るためです。 // グラフを最初に作図して、範囲の確認をします。 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, VCLTee.Series, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) Chart1: TChart; Series1: TLineSeries; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; BitBtn1: TBitBtn; Memo1: TMemo; Series3: TPointSeries; Series4: TPointSeries; LabeledEdit3: TLabeledEdit; LabeledEdit4: TLabeledEdit; BitBtn2: TBitBtn; CheckBox1: TCheckBox; procedure BitBtn1Click(Sender: TObject); procedure BitBtn2Click(Sender: TObject); procedure LabeledEdit1Change(Sender: TObject); procedure LabeledEdit2Change(Sender: TObject); procedure LabeledEdit3Change(Sender: TObject); procedure LabeledEdit4Change(Sender: TObject); procedure CheckBox1Click(Sender: TObject); private { Private 宣言 } procedure chart_graph(gl, gr: double); public { Public 宣言 } end; var Form1: TForm1; implementation uses Velthuis.Bigdecimals, Velthuis.bigintegers, big_Math; {$R *.dfm} { function BigdecimalToDouble(b: bigdecimal): double; var bigstr : string; absb : bigdecimal; begin absb := bigdecimal.Abs(b); if absb = bigdecimal.Zero then begin result := 0; exit; end; if absb >= maxdouble then begin result := maxdouble; if b < bigdecimal.Zero then result := -result; exit; end; if absb <= mindouble then begin result := mindouble; if b < bigdecimal.Zero then result := -result; exit; end; b := b.RoundToPrecision(30); bigstr := b.ToString; result := strtofloat(bigstr); end; } // 関数f(x)の計算式 非線形方程式 bigdecimal function f(x: bigdecimal): bigdecimal; begin result := (x - 3) * (x - 3) - 2; // result := x * x; if form1.CheckBox1.Checked = true then result := -result; end; // 区間[gl,gr]の関数f(x)のグラフを作図 procedure TForm1.chart_graph(gl, gr: double); const n = 100; var x, xs, xe, dx: double; y : double; i : integer; begin series1.clear; series3.clear; series4.clear; if gl = gr then exit; // 範囲がゼロだったら終了 xs := gl; xe := gr; dx := (xe - xs) / n; for i := 0 to n do begin x := xs + i * dx; y := bigdecimaltodouble(f(x)); series1.AddXY(x, y); end; end; // 頂点の近似値計算 function bisection_method(a, p, epsilon: bigdecimal; var loop: integer): bigdecimal; var fn, fa: bigdecimal; chf : boolean; begin // 初期指定点とピッチ確認 fn := f(a); // 初期点計算 fa := f(a + p); chf := false; if form1.CheckBox1.Checked = true then begin if fn > fa then chf := true; // 上向き頂点 end else begin if fn < fa then chf := true; // 下向き頂点 最下点 end; if chf then begin result := 0; exit; end; // 頂点検出 repeat chf := false; fa := fn; // 前の値 a := a + p; // 次の点 fn := f(a); // 次の点計算 if form1.CheckBox1.Checked = true then begin if fn < fa then chf := true; // 上向き頂点 end else begin if fn > fa then chf := true; // 下向き頂点 最下点 end; if chf then begin a := a - p - p; // 2ピッチ戻し p := p / 4; fn := f(a); // 元の値再計算 end; inc(loop); until (p < epsilon * (bigdecimal.abs(a) + 1)) or (loop > 5000); result := a; end; // 計算実行 procedure TForm1.BitBtn1Click(Sender: TObject); var a, p, alpha, y : bigdecimal; loop, prec : integer; epsilon : bigdecimal; estr : string; yd, ad : double; begin a := labelededit1.Text; p := labelededit2.Text; memo1.Clear; // 収束判定値計算 // 非線形方程式の計算 prec := bigdecimal.DefaultPrecision; prec := prec - 1; estr := '1e-' + intTostr(prec); epsilon := estr; loop := 0; alpha := bisection_method(a, p, epsilon, loop); if loop = 0 then begin application.MessageBox('初期値の位置に間違いがある、又はピッチが大きすぎます。','注意',0); exit; end; // 検算 y := f(alpha); yd := bigdecimaltodouble(y); ad := bigdecimaltodouble(alpha); // 計算結果表示 series4.AddXY(ad, yd); if checkbox1.Checked = true then memo1.Lines.Append('f(x) = - ((x - 3)^2 - 2)') else memo1.Lines.Append('f(x) = (x - 3)^2 - 2'); memo1.Lines.Append('ループ数 ' + intTostr(loop)); memo1.Lines.Append('収束判定値'); memo1.Lines.Append(epsilon.ToString); memo1.Lines.Append('x= ' + floatTostr(ad)); memo1.Lines.Append('検算 y = f(x)'); memo1.Lines.Append('y= ' + floatTostr(yd)); end; procedure TForm1.BitBtn2Click(Sender: TObject); var gl, gr : double; ch : integer; a, p, y : double; begin val(labelededit3.Text, gl, ch); if ch <> 0 then begin application.MessageBox('グラフ範囲左に間違いが有ります。','注意',0); exit; end; val(labelededit4.Text, gr, ch); if ch <> 0 then begin application.MessageBox('グラフ範囲右に間違いが有ります。','注意',0); exit; end; if gr <= gl then begin application.MessageBox('グラフ範囲右には左より大きくして下さい。','注意',0); exit; end; chart_graph(gl, gr); application.ProcessMessages; val(labelededit1.Text, a, ch); if ch <> 0 then begin application.MessageBox('初期値aに間違いが有ります。','注意',0); exit; end; val(labelededit2.Text, p, ch); if ch <> 0 then begin application.MessageBox('初期間隔pに間違いが有ります。','注意',0); exit; end; if (a < gl) or (a > gr) then begin application.MessageBox('初期値aがグラフの範囲外です。','注意',0); exit; end; if a > (gr - gl) / 2 + gl then begin application.MessageBox('初期値aは左寄りにして下さい。','注意',0); exit; end; y := bigdecimaltodouble(f(a)); series3.AddXY(a, y); application.ProcessMessages; if p > (gr - gl) / 2 then begin application.MessageBox('初期間隔pが大きすぎます。','注意',0); exit; end; if p <= 0 then begin application.MessageBox('初期間隔pはゼロより大きくして下さい。','注意',0); exit; end; y := bigdecimaltodouble(f(a + p)); series4.AddXY(a + p, y); application.ProcessMessages; bitbtn1.Enabled := True; end; procedure TForm1.LabeledEdit1Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit2Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit3Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit4Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.CheckBox1Click(Sender: TObject); begin bitbtn1.Enabled := false; memo1.Clear; series1.clear; series3.clear; series4.clear; end; end.
非線形方程式と傾きを指定された直線との接点計算
非線形方程式y=f(x)で、指定されたxの範囲の最小値(最下点)あるいは最大値(最上点)を求める計算の応用です。
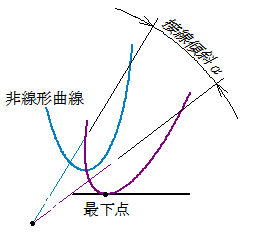
直線 y=αx
直線の傾きをαとすると、非線形方程式の値を、-α 分座標変換して最小値(最下点)あるいは最大値(最上点)をを求めます。
座標変換に三角関数を使用する為、計算の誤差が大きくなると同時に、計算繰り返し数が多くなります。
微分が出来れば、簡単に直線の方程式を導き出せます。
プログラムは例なので微分できる方程式を使用しています。
プログラム
// 非線形方程式と傾き指定の接線計算 // 非線形lineを-傾き分座標変換して頂点として計算します。 // 非線形方程式の頂点又は接線検出 // 頂点のx軸方向の値は、誤差が大きくなります、頂点は水平に成るためです。 // グラフを最初に作図して、範囲の確認をします。 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, VCLTee.Series, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) Chart1: TChart; Series1: TLineSeries; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; BitBtn1: TBitBtn; Memo1: TMemo; Series3: TPointSeries; Series4: TPointSeries; LabeledEdit3: TLabeledEdit; LabeledEdit4: TLabeledEdit; BitBtn2: TBitBtn; CheckBox1: TCheckBox; LabeledEdit5: TLabeledEdit; Series2: TLineSeries; procedure BitBtn1Click(Sender: TObject); procedure BitBtn2Click(Sender: TObject); procedure LabeledEdit1Change(Sender: TObject); procedure LabeledEdit2Change(Sender: TObject); procedure LabeledEdit3Change(Sender: TObject); procedure LabeledEdit4Change(Sender: TObject); procedure CheckBox1Click(Sender: TObject); procedure LabeledEdit5Change(Sender: TObject); private { Private 宣言 } procedure chart_graph(gl, gr: double); public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} // x, y 座標 // q : 角度(rad) // xt, yt 変換後座標 procedure transformation(x, y, q : double; var xt, yt : double); var qt, ysx, l : double; begin if x <> 0 then begin ysx := y / x; qt := arctan(ysx); end else qt := pi / 2; qt := qt + q; l := x * x + y * y; l := Sqrt(l); xt := cos(qt) * l; yt := sin(qt) * l; end; // 関数f(x)の計算式 非線形方程式 // f(x) = (x-3)^2 - 2 // f'(x) = x / 2 - 6 // 傾きαの接線のx座標 α= x/2-6, x= (α+6)/2 function f(x: double): double; begin result := (x - 3) * (x - 3) - 2; // result := x * x; if form1.CheckBox1.Checked = true then result := -result; end; // グラフ範囲内 傾き確認 // gl グラフ左端 // gr グラフ右端 // a 直線傾き // チェックピッチ function tiltcheck(gl, gr, a, p: double): boolean; var sx, ex, sy, ey, sa, ea : double; n, i : integer; begin result := false; p := p / 10; n := round((gr - gl) / p); sx := gl; sy := f(gl); ex := gl + p; ey := f(ex); sa := (ey - sy) / (ex - sx) - a; for i := 2 to n do begin sx := ex; sy := ey; ex := gl + i * p; ey := f(ex); ea := (ey - sy) / (ex - sx) - a; if ea * sa <= 0 then begin result := true; break; end; sa := ea; end; end; // 線分 procedure line_segment(x, y, a, gl, gr: double); var c : double; begin c := y - a * x; y := a * gl + c; form1.Series2.AddXY(gl, y); y := a * gr + c; Form1.Series2.AddXY(gr, y); Form1.Memo1.Lines.Append('接線式'); if c >= 0 then Form1.Memo1.Lines.Append(' y = ' + floatTostr(a) + 'x + ' + floatTostr(c)) else Form1.Memo1.Lines.Append(' y = ' + floatTostr(a) + 'x ' + floatTostr(c)) end; // 区間[gl,gr]の関数f(x)のグラフを作図 procedure TForm1.chart_graph(gl, gr: double); const n = 100; var x, xs, xe, dx: double; y : double; i : integer; begin series1.clear; series2.clear; series3.clear; series4.clear; if gl = gr then exit; // 範囲がゼロだったら終了 xs := gl; xe := gr; dx := (xe - xs) / n; for i := 0 to n do begin x := xs + i * dx; y := f(x); series1.AddXY(x, y); end; end; // 頂点の近似値計算 function bisection_method(a, p, q, epsilon: double; var loop: integer): double; var fn, fa, fnt, fat: double; nt, at : double; chf : boolean; begin q := arctan(q); fn := f(a); // 初期点計算 transformation(a, fn, q, at, fnt); a := a + p; // 次の点 fa := f(a); // 次の点計算 transformation(a, fa, q, nt, fat); chf := false; if form1.CheckBox1.Checked = true then begin if fnt > fat then chf := true; // 上向き頂点 end else begin if fnt < fat then chf := true; // 下向き頂点 最下点 end; if chf then begin result := 0; exit; end; // 頂点の計算 repeat chf := false; fat := fnt; // 前の値保存 a := a + p; // 次の計算点 fn := f(a); // 次の点計算 transformation(a, fn, q, nt, fnt); if form1.CheckBox1.Checked = true then begin if fnt < fat then chf := true; // 上向き頂点 end else begin if fnt > fat then chf := true; // 下向き頂点 最下点 end; if chf then begin a := a - p - p; // 2ピッチ戻し p := p / 4; fn := f(a); // 元の値再計算 transformation(a, fn, q, nt, fnt); end; inc(loop); until (p < epsilon * (abs(a) + 1)) or (loop > 500); result := a; end; // 計算実行 procedure TForm1.BitBtn1Click(Sender: TObject); var a, p, alpha, y, q, gr, gl : double; loop : integer; epsilon, tmp : double; begin q := strTofloat(labelededit5.Text); a := strTofloat(labelededit1.Text); p := strTofloat(labelededit2.Text); gl := strTofloat(labelededit3.Text); gr := strTofloat(labelededit4.Text); memo1.Clear; // 収束判定値計算 epsilon := 1; repeat epsilon := epsilon / 2; tmp := 1 + epsilon; until tmp = 1; epsilon := epsilon * 2; // 非線形方程式の計算 loop := 0; alpha := bisection_method(a, p, -q, epsilon, loop); if loop = 0 then begin application.MessageBox('初期値の位置に間違いがある、又はピッチが大きすぎます。','注意',0); exit; end; // 検算 y := f(alpha); // 計算結果表示 series4.AddXY(alpha, y); memo1.Lines.Append('f(x) = (x - 3)^2 - 2'); memo1.Lines.Append('ループ数 ' + intTostr(loop)); memo1.Lines.Append('収束判定値'); memo1.Lines.Append(floatTostr(epsilon)); memo1.Lines.Append('x= ' +floatTostr(alpha)); memo1.Lines.Append('検算 y = f(x)'); memo1.Lines.Append('y= ' +floatTostr(y)); line_segment(alpha, y, q, gl, gr); end; procedure TForm1.BitBtn2Click(Sender: TObject); var gl, gr : double; ch : integer; a, p, y, q : double; begin val(labelededit3.Text, gl, ch); if ch <> 0 then begin application.MessageBox('グラフ範囲左に間違いが有ります。','注意',0); exit; end; val(labelededit4.Text, gr, ch); if ch <> 0 then begin application.MessageBox('グラフ範囲右に間違いが有ります。','注意',0); exit; end; if gr <= gl then begin application.MessageBox('グラフ範囲右には左より大きくして下さい。','注意',0); exit; end; chart_graph(gl, gr); application.ProcessMessages; val(labelededit1.Text, a, ch); if ch <> 0 then begin application.MessageBox('初期値aに間違いが有ります。','注意',0); exit; end; val(labelededit2.Text, p, ch); if ch <> 0 then begin application.MessageBox('初期間隔pに間違いが有ります。','注意',0); exit; end; if (a < gl) or (a > gr) then begin application.MessageBox('初期値aがグラフの範囲外です。','注意',0); exit; end; if a > (gr - gl) / 2 + gl then begin application.MessageBox('初期値aは左寄りにして下さい。','注意',0); exit; end; val(labelededit5.Text, q, ch); if ch <> 0 then begin application.MessageBox('直線の傾きに間違いが有ります。','注意',0); exit; end; y := f(a); series3.AddXY(a, y); application.ProcessMessages; if p > (gr - gl) / 2 then begin application.MessageBox('初期間隔pが大きすぎます。','注意',0); exit; end; if p <= 0 then begin application.MessageBox('初期間隔pはゼロより大きくして下さい。','注意',0); exit; end; y := f(a + p); series4.AddXY(a + p, y); if not tiltcheck(a, gr, q, p) then begin application.MessageBox('計算範囲内(初期値～グラフ範囲右)に指定の傾きは有りません。','注意',0); exit; end; application.ProcessMessages; bitbtn1.Enabled := True; end; procedure TForm1.LabeledEdit1Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit2Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit3Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit4Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit5Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.CheckBox1Click(Sender: TObject); begin bitbtn1.Enabled := false; end; end.
bigdecimalによるプログラム
演算桁数が多いため、計算に非常に時間がかかります。
// 非線形方程式と傾き指定の接線計算 // 非線形lineを-傾き分座標変換して頂点として計算します。 // 非線形方程式の頂点又は接線検出 // 頂点のx軸方向の値は、誤差が大きくなります、頂点は水平に成るためです。 // グラフを最初に作図して、範囲の確認をします。 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, VCLTee.Series, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart, system.Math; type TForm1 = class(TForm) Chart1: TChart; Series1: TLineSeries; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; BitBtn1: TBitBtn; Memo1: TMemo; Series3: TPointSeries; Series4: TPointSeries; LabeledEdit3: TLabeledEdit; LabeledEdit4: TLabeledEdit; BitBtn2: TBitBtn; CheckBox1: TCheckBox; LabeledEdit5: TLabeledEdit; Series2: TLineSeries; procedure BitBtn1Click(Sender: TObject); procedure BitBtn2Click(Sender: TObject); procedure LabeledEdit1Change(Sender: TObject); procedure LabeledEdit2Change(Sender: TObject); procedure LabeledEdit3Change(Sender: TObject); procedure LabeledEdit4Change(Sender: TObject); procedure CheckBox1Click(Sender: TObject); procedure LabeledEdit5Change(Sender: TObject); private { Private 宣言 } procedure chart_graph(gl, gr: double); public { Public 宣言 } end; var Form1: TForm1; implementation uses Velthuis.Bigdecimals, Velthuis.bigintegers, big_math; {$R *.dfm} { // Bigdecimal -> Double function BigdecimalToDouble(b: bigdecimal): double; var bigstr : string; absb : bigdecimal; begin absb := bigdecimal.Abs(b); if absb = bigdecimal.Zero then begin result := 0; exit; end; if absb >= maxdouble then begin result := maxdouble; if b < bigdecimal.Zero then result := -result; exit; end; if absb <= mindouble then begin result := mindouble; if b < bigdecimal.Zero then result := -result; exit; end; b := b.RoundToPrecision(30); bigstr := b.ToString; result := strtofloat(bigstr); end; } // 座標変換 // x, y 座標 // q : 角度(rad) // xt, yt 変換後座標 // 誤差を小さくする為50％程有効桁数を大きくします。 procedure transformation(x, y, q : bigdecimal; var xt, yt : bigdecimal); var qt, ysx, l : bigdecimal; pre : integer; begin pre := bigdecimal.DefaultPrecision; bigdecimal.DefaultPrecision := pre + pre div 2; // 50％程有効桁数up if x <> 0 then begin ysx := y / x; qt := arctan_big(ysx); end else qt := pi_big / 2; qt := qt + q; l := x * x + y * y; l := l.Sqrt(l); xt := cos_big(qt) * l; yt := sin_big(qt) * l; bigdecimal.DefaultPrecision := pre; end; // 関数f(x)の計算式 非線形方程式 // f(x) = (x-3)^2 - 2 // f'(x) = x / 2 - 6 // 傾きαの接線のx座標 α= x/2-6, x= (α+6)/2 function f(x: bigdecimal): bigdecimal; begin result := (x - 3) * (x - 3) - 2; // result := x * x; if form1.CheckBox1.Checked = true then result := -result; end; // グラフ範囲内 傾き確認 // gl グラフ左端 // gr グラフ右端 // a 直線傾き // チェックピッチ function tiltcheck(gl, gr, a, p: double): boolean; var sx, ex, sy, ey, sa, ea : double; n, i : integer; begin result := false; p := p / 10; n := round((gr - gl) / p); sx := gl; sy := bigdecimaltodouble(f(gl)); ex := gl + p; ey := bigdecimaltodouble(f(ex)); sa := (ey - sy) / (ex - sx) - a; for i := 2 to n do begin sx := ex; sy := ey; ex := gl + i * p; ey := bigdecimaltodouble(f(ex)); ea := (ey - sy) / (ex - sx) - a; if ea * sa <= 0 then begin result := true; break; end; sa := ea; end; end; // 接線 procedure line_segment(x, y, a, gl, gr: double); var c : double; begin c := y - a * x; y := a * gl + c; form1.Series2.AddXY(gl, y); y := a * gr + c; Form1.Series2.AddXY(gr, y); Form1.Memo1.Lines.Append('接線式'); if c >= 0 then Form1.Memo1.Lines.Append(' y = ' + floatTostr(a) + 'x + ' + floatTostr(c)) else Form1.Memo1.Lines.Append(' y = ' + floatTostr(a) + 'x ' + floatTostr(c)) end; // 区間[gl,gr]の関数f(x)のグラフを作図 procedure TForm1.chart_graph(gl, gr: double); const n = 100; var x, xs, xe, dx: double; y : double; i : integer; begin series1.clear; series2.clear; series3.clear; series4.clear; if gl = gr then exit; // 範囲がゼロだったら終了 xs := gl; xe := gr; dx := (xe - xs) / n; for i := 0 to n do begin x := xs + i * dx; y := bigdecimalTodouble(f(x)); series1.AddXY(x, y); end; end; // 傾斜頂点の近似値計算 function bisection_method(x, p, q, epsilon: bigdecimal; var loop: integer): bigdecimal; var yn, ya, ynt, yat : bigdecimal; xnt, xat : bigdecimal; chf : boolean; begin q := -arctan_big(q); // 傾きαを角度(rad)に yn := f(x); // 初期点計算 transformation(x, yn, q, xnt, ynt); // 座標変換 x := x + p; // 次の点 ya := f(x); // 次の点計算 transformation(x, ya, q, xat, yat); // 座標変換 chf := false; if form1.CheckBox1.Checked = true then begin if ynt > yat then chf := true; // 上向き頂点 end else begin if ynt < yat then chf := true; // 下向き頂点 最下点 end; if chf then begin result := 0; exit; end; // 頂点の計算 repeat chf := false; yat := ynt; x := x + p; yn := f(x); // 初期点計算 transformation(x, yn, q, xnt, ynt); // 座標変換 if form1.CheckBox1.Checked = true then begin if ynt < yat then chf := true; // 上向き頂点 end else begin if ynt > yat then chf := true; // 下向き頂点 最下点 end; if chf then begin x := x - p - p; // 2ピッチ戻し p := p / 4; yn := f(x); // 元の値再計算 transformation(x, yn, q, xnt, ynt); // 座標変換 end; transformation(x, yn, q, xnt, ynt); // 座標変換 inc(loop); until (p < epsilon * (bigdecimal.Abs(x) + 1)) or (loop > 5000); result := x.RoundToPrecision(bigdecimal.DefaultPrecision); end; // 計算実行 procedure TForm1.BitBtn1Click(Sender: TObject); var x, y, q, gr, gl : double; loop, pre : integer; ab, pb, qb : bigdecimal; epsilon, xbig: bigdecimal; epstr : string; begin q := strTofloat(labelededit5.Text); gl := strTofloat(labelededit3.Text); gr := strTofloat(labelededit4.Text); qb := labelededit5.Text; ab := labelededit1.Text; pb := labelededit2.Text; memo1.Clear; // 収束判定値計算 pre := bigdecimal.DefaultPrecision; epstr := '1E-' + inttostr(pre * 4 div 5); epsilon := epstr; // 非線形方程式の計算 loop := 0; xbig := bisection_method(ab, pb, qb, epsilon, loop); if loop = 0 then begin application.MessageBox('初期値の位置に間違いがある、又はピッチが大きすぎます。','注意',0); exit; end; x := bigdecimaltodouble(xbig); // 検算 y := bigdecimalTodouble(f(xbig)); // 計算結果表示 series4.AddXY(x, y); memo1.Lines.Append('f(x) = (x - 3)^2 - 2'); memo1.Lines.Append('ループ数 ' + intTostr(loop)); memo1.Lines.Append('収束判定値 ' + epsilon.ToString); memo1.Lines.Append('x= ' +floatTostr(x)); memo1.Lines.Append('検算 y = f(x)'); memo1.Lines.Append(' y= ' + floatTostr(y)); // memo1.Lines.Append(xbig.ToString); line_segment(x, y, q, gl, gr); // 接線描画 end; // 入力値確認 初期グラフ作図 procedure TForm1.BitBtn2Click(Sender: TObject); var gl, gr : double; ch : integer; a, p, y, q : double; begin val(labelededit3.Text, gl, ch); if ch <> 0 then begin application.MessageBox('グラフ範囲左に間違いが有ります。','注意',0); exit; end; val(labelededit4.Text, gr, ch); if ch <> 0 then begin application.MessageBox('グラフ範囲右に間違いが有ります。','注意',0); exit; end; if gr <= gl then begin application.MessageBox('グラフ範囲右には左より大きくして下さい。','注意',0); exit; end; chart_graph(gl, gr); application.ProcessMessages; val(labelededit1.Text, a, ch); if ch <> 0 then begin application.MessageBox('初期値aに間違いが有ります。','注意',0); exit; end; val(labelededit2.Text, p, ch); if ch <> 0 then begin application.MessageBox('初期間隔pに間違いが有ります。','注意',0); exit; end; if (a < gl) or (a > gr) then begin application.MessageBox('初期値aがグラフの範囲外です。','注意',0); exit; end; if a > (gr - gl) / 2 + gl then begin application.MessageBox('初期値aは左寄りにして下さい。','注意',0); exit; end; val(labelededit5.Text, q, ch); if ch <> 0 then begin application.MessageBox('直線の傾きに間違いが有ります。','注意',0); exit; end; y := bigdecimaltodouble(f(a)); series3.AddXY(a, y); application.ProcessMessages; if p > (gr - gl) / 2 then begin application.MessageBox('初期間隔pが大きすぎます。','注意',0); exit; end; if p <= 0 then begin application.MessageBox('初期間隔pはゼロより大きくして下さい。','注意',0); exit; end; y := bigdecimaltodouble(f(a + p)); series4.AddXY(a + p, y); if not tiltcheck(a, gr, q, p) then begin application.MessageBox('計算範囲内(初期値～グラフ範囲右)に指定の傾きは有りません。','注意',0); exit; end; application.ProcessMessages; bitbtn1.Enabled := True; end; procedure TForm1.LabeledEdit1Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit2Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit3Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit4Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.LabeledEdit5Change(Sender: TObject); begin bitbtn1.Enabled := false; end; procedure TForm1.CheckBox1Click(Sender: TObject); begin bitbtn1.Enabled := false; end; end.
vertex_calculator_big.zip
三角関数、逆三角関数、その他関数、 連立一次方程式の解法 に戻る