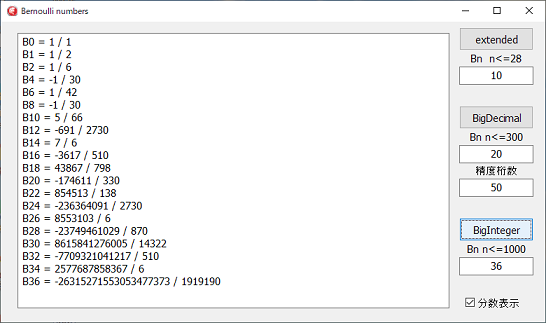
 プログラムのBigDecimalでの計算は分数計算をしていて、浮動小数点での表示と、分数での表示を切り替えることが出来ます。
プログラムのBigDecimalでの計算は分数計算をしていて、浮動小数点での表示と、分数での表示を切り替えることが出来ます。分数で表示する場合は、分子の大きさに合わせて、精度桁数の設定を変えます。
分数表示で、小数点が現れる場合は、精度桁数を大きくしてください。
此処の計算アルゴリズムでは、B1の値が+になります。
間違いではありません。
B1のベルヌーイ数は、条件によってマイナスの値と、プラスの値を取ることが知られています。
新しい、ベルヌーイ数表のB1の値は±1/2となっています。
2021-12-8 BigDecimalでの計算時間が余りにも長いので、BigIntegerの計算を追加しました。
ベルヌーイ数 その4
ベルヌーイ数計算のアルゴリズムにAkiyama-Tanigawa algorithmを使用したプログラムを検討しました。
Akiyama-Tanigawa algorithmは、インターネットで検索すると、論文を見つける事ができるので、それを参照してください。
論文の中には、プログラムについての記載はありません、論文の内容から、そのアルゴリズムのプログラムが作られています。
二項係数の計算も階乗も使用していないので、非常に簡単なプログラムとなっています。
(ベルヌーイ数 その2、ベルヌーイ数 その3でも二項係数の計算も階乗も使用していませんが、全て正の値として計算されるため、符号付加のルーチンが必要となります。)
また、今回はMPArithではなく、Rudy's Delphi CornerのBigDecimalを使用します。
此処には、Bigintegerもあります。
特徴として、四則演算 + - * / 等がそのまま利用できることです。
但し、三角関数や対数関数はありません。
Rudy's Delphi Cornerを開いたら
-> Free Coad -> Bigintegers for Delphi 又は
BigDecimals for Delph -> 上の行の最後のリンク DelphiBigNumbers
project on GitHub ->
Coad▼ ->
Download ZIP でダウンロードします。
DelphiBigNumbers-master.zip がダウンロード出来たら、解凍したSorce フォルダーを、適当な場所にコピーして、そこへパス(ツール->オプション->Delphiオプション->ライブラリ->ライブラリパス)を追加し、usesに Velthuis.BigDecimals Velthuis.BigIntegers を追加すれば、BigDecimal Biginteger が使用可能となります。
使用方法は、解凍されたPDFファイルを参照してください。
 プログラムのBigDecimalでの計算は分数計算をしていて、浮動小数点での表示と、分数での表示を切り替えることが出来ます。
プログラムのBigDecimalでの計算は分数計算をしていて、浮動小数点での表示と、分数での表示を切り替えることが出来ます。
分数で表示する場合は、分子の大きさに合わせて、精度桁数の設定を変えます。
分数表示で、小数点が現れる場合は、精度桁数を大きくしてください。
此処の計算アルゴリズムでは、B1の値が+になります。
間違いではありません。
B1のベルヌーイ数は、条件によってマイナスの値と、プラスの値を取ることが知られています。
新しい、ベルヌーイ数表のB1の値は±1/2となっています。
BigDecimalでの計算では、ベルヌーイNoが300を超えると、演算時間が異常に長くなります。
BigIntegerのプログラムも追加してみましたが、これでもベルヌーイNoを1000にすると、いつ計算が終わるか心配になる位時間が掛かります。
ベルヌーイ数 その3 での計算が、一番早く計算ができます。
プログラム
// reference http://rvelthuis.de/programs/bigintegers.html unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls; type TForm1 = class(TForm) Memo1: TMemo; BitBtn1: TBitBtn; LabeledEdit1: TLabeledEdit; BitBtn2: TBitBtn; LabeledEdit2: TLabeledEdit; CheckBox1: TCheckBox; LabeledEdit3: TLabeledEdit; BitBtn3: TBitBtn; LabeledEdit4: TLabeledEdit; procedure BitBtn1Click(Sender: TObject); procedure BitBtn2Click(Sender: TObject); procedure BitBtn3Click(Sender: TObject); private { Private 宣言 } public { Public 宣言 } end; var Form1: TForm1; implementation uses Velthuis.BigDecimals, Velthuis.BigIntegers; {$R *.dfm} // 浮動小数点の剰余 function fmod(x, y: extended): extended; var tmp: extended; n : integer; begin tmp := x / y; n := trunc(tmp); result := x - y * n; end; // 最大公約数 ユークリッドの互除法 extended function gcd(x, y: extended): extended; var t : extended; n : integer; begin n := 0; while y <> 0 do begin inc(n); t := fmod(x, y); x := y; y := t; if n > 100 then break; end; result := Abs(x); end; // Akiyama-Tanigawa algorithm procedure Bernoulli_number(n : integer); var a, b : array of extended; tmpn, tmpd, g : extended; m, j : integer; begin setlength(a, n + 1); setlength(b, n + 1); for m := 0 to n do begin a[m] := 1; b[m] := m + 1; for j := m - 1 downto 0 do begin tmpn := a[j] * b[j + 1] - a[j + 1] * b[j]; tmpn := tmpn * (j + 1); tmpd := b[j] * b[j + 1]; g := gcd(tmpn, tmpd); a[j] := tmpn / g; b[j] := tmpd / g; end; if (m = 1) or (m mod 2 = 0) then begin if form1.CheckBox1.checked = true then Form1.memo1.Lines.Append('B' + intTostr(m) + ' = ' + floatTostr(a[0]) + ' / ' + floatTostr(b[0])) else Form1.memo1.Lines.Append('B' + intTostr(m) + ' = ' + floatTostr(a[0] / b[0])); end; end; end; procedure TForm1.BitBtn1Click(Sender: TObject); var n, c : integer; begin memo1.Clear; val(labeledEdit1.Text, n, c); if c <> 0 then begin Memo1.Text := 'nの値に間違いがあります。'; exit; end; n := abs(n); if n > 28 then begin Memo1.Text := 'nの値は28迄にして下さい。'; exit; end; Bernoulli_number(n); end; // 最大公約数 ユークリッドの互除法 BigDecimal function gcd_BigDecimal(x, y: BigDecimal): BigDecimal; var t : BigDecimal; begin while y <> 0 do begin t := x mod y; x := y; y := t; end; result := BigDecimal.Abs(x); end; // Akiyama-Tanigawa algorithm // BigDecimal procedure Bernoulli_number_BigDecimal(n: integer); var m, j : integer; a : array of BigDecimal; // 分子 b : array of BigDecimal; // 分母 tmpN : BigDecimal; // 分子 tmpD : BigDecimal; // 分母 tmp : BigDecimal; gcd : BigDecimal; // 最大公約数 begin setlength(a, n + 1); setlength(b, n + 1); for m := 0 to n do begin a[m] := BigDecimal.One; // 分子 初期値 b[m] := (m + 1); // 分母 初期値 for j := m - 1 downto 0 do begin tmpN := a[j] * b[j + 1] - a[j + 1] * b[j]; // 分子 tmpN := tmpN * (j + 1); // 〃 tmpD := b[j] * b[j + 1]; // 分母 gcd := gcd_BigDecimal(tmpN, tmpD); // 最大公約数 a[j] := tmpN / gcd; b[j] := tmpD / gcd; end; if (n <= 40) or (n = m) then if (m = 1) or (m mod 2 = 0) then if form1.CheckBox1.checked = true then Form1.memo1.Lines.Append('B' + intTostr(m) + ' = ' + a[0].tostring + ' / ' + b[0].tostring) else begin tmp := a[0] / b[0]; Form1.memo1.Lines.Append('B' + intTostr(m) + ' = ' + tmp.tostring) end; end; end; procedure TForm1.BitBtn2Click(Sender: TObject); var n, k , c : integer; begin memo1.Clear; val(labeledEdit2.Text, n, c); if c <> 0 then begin Memo1.Text := 'nの値に間違いがあります。'; exit; end; n := abs(n); if n mod 2 <> 0 then begin memo1.Text := 'BigInteger計算のベルヌーイnの値は偶数にして下さい。'; exit; end; if n > 300 then begin memo1.Text := 'BigInteger計算のベルヌーイnの値は300迄にして下さい。'; exit; end; val(labeledEdit3.Text, k, c); if c <> 0 then begin Memo1.Text := '精度桁数の値に間違いがあります。'; exit; end; BigDecimal.DefaultPrecision := k; Bernoulli_number_BigDecimal(n); end; // 最大公約数 ユークリッドの互除法 BigInteger function gcd_BigInteger(x, y: BigInteger): BigInteger; var t : BigInteger; begin while y <> 0 do begin t := x mod y; x := y; y := t; end; result := BigInteger.Abs(x); end; // Akiyama-Tanigawa algorithm // BigInteger procedure Bernoulli_number_BigInteger(n: integer); var m, j : integer; a : array of BigInteger; // 分子 b : array of BigInteger; // 分母 tmpN : BigInteger; // 分子 tmpD : BigInteger; // 分母 gcd : BigInteger; // 最大公約数 Bn, Bd, tmp : BigDecimal; begin setlength(a, n + 1); setlength(b, n + 1); for m := 0 to n do begin a[m] := 1; // 分子 初期値 b[m] := (m + 1); // 分母 初期値 for j := m - 1 downto 0 do begin tmpN := a[j] * b[j + 1] - a[j + 1] * b[j]; // 分子 tmpN := tmpN * (j + 1); // 〃 tmpD := b[j] * b[j + 1]; // 分母 gcd := gcd_BigInteger(tmpN, tmpD); // 最大公約数 a[j] := tmpN div gcd; b[j] := tmpD div gcd; end; if (n <= 40) or (n = m) then if (m = 1) or (m mod 2 = 0) then if form1.CheckBox1.checked = true then Form1.memo1.Lines.Append('B' + intTostr(m) + ' = ' + a[0].tostring + ' / ' + b[0].tostring) else begin Bn := a[0]; Bd := b[0]; tmp := Bn / Bd; Form1.memo1.Lines.Append('B' + intTostr(m) + ' = ' + tmp.ToString); end; end; end; procedure TForm1.BitBtn3Click(Sender: TObject); var n, c : integer; begin val(labelededit4.Text, n, c); if c <> 0 then begin memo1.Text := 'BigInteger計算のベルヌーイnの値に間違いがあります。'; exit; end; n := abs(n); if n mod 2 <> 0 then begin memo1.Text := 'BigInteger計算のベルヌーイnの値は偶数にして下さい。'; exit; end; if n > 1000 then begin memo1.Text := 'BigInteger計算のベルヌーイnの値は1000迄にして下さい。'; exit; end; memo1.Clear; Bernoulli_number_BigInteger(n); end; end.
![]() Bernoulli_number_extended.zip
Bernoulli_number_extended.zip
各種プログラム計算例に戻る