2021-12-15 参考にCのプログラム追加
2021-12- 01 mpf_set_default_decprec による演算有効桁数変更について追記
ベルヌーイ数 その２
ベルヌーイ数 その１のでは、B18程度迄で、浮動小数点の結果しか得られなかったので、もう少し大きなBnが得られるプログラムを検討してみました。
元のプログラムはインターネットで探し出して来たものです。(C言語による最新アルゴリズム事典からダウンロードしたBernoull.cを基本にしています。)
このプログラムは、ベルヌーイ数をすべて正の値で計算します、そこで、ベルヌーイ数計算後に、負の値になるベルヌーイNoの値を負数に変更しています。
浮動小数点を使用していますが、計算は、分子と分母に分けて、分数計算としています。
浮動小数点でも、有効桁数が、整数表現をできる範囲であれば分数表示とし、それを超えた値となった場合は、浮動小数点表示になります。
分母は、2n(2n-1)で分子も単純な計算の繰り返しだけなので非常に高速に計算ができます。
Cのプログラム
このプログラムは、多倍長のプログラムと一緒にダウンロードができ、実行はDOS窓でなされます。
/***********************************************************
bernoull.c -- Bernoulli (ベルヌーイ) 数
***********************************************************/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <float.h>
double gcd(double x, double y) /* 最大公約数 */
{
double t;
while (y != 0) { t = fmod(x, y); x = y; y = t; }
return x;
}
#define N 40
int main()
{
int i, n;
double q, b1, b2, bc, d;
static double t[N + 1];
char s[4] = " = ";
double invEP = 1 / DBL_EPSILON;
/* B0 */
n = 0;
b1 = 1;
printf(" B(%2d) = %.0f\n", n, b1);
/* B1 */
n = 1;
// b1 = -1;
b2 = 2;
printf(" B(%2d) =±%.0f/%.0f\n", n, b1, b2);
/* B2～ */
q = 1; /* 分母初期値 */
t[1] = 1; /* 分子初期値 */
for (n = 2; n <= N; n++) {
for (i = 1; i < n; i++) t[i - 1] = i * t[i]; /* 分子計算 */
t[n - 1] = 0; /* 〃 */
for (i = n; i >= 2; i--) t[i] += t[i - 2]; /* 〃 */
if (n % 2 == 0) { /* n偶数なら */
b1 = n * t[0]; /* 分子計算 */
bc = b1;
q *= 4; /* 分母計算 */
b2 = q * (q - 1); /* 〃 */
if (n % 4 == 0) { b1 *= -1; s[3] = '\0'; /* nが4の倍数の時 -b1 */
} else s[3] = ' ';
/* 小数部有無の判別 */
if (bc < invEP && b2 < invEP) { /* 小数部無 */
d = gcd(bc, b2); /* d 最大公約数 */
b1 /= d;
b2 /= d;
printf(" B(%2d)%s%.0f/%.0f\n", n, s, b1, b2); /* 分数表記 */
} else { /* 小数部有 */
printf(" B(%2d)%s%.10g\n", n, s, b1 / b2); /* 浮動小数点表記 */
}
}
}
printf("\n Enterキーを押して下さい");
getchar();
return EXIT_SUCCESS;
}
Delphiのプログラム
次のプログラムは上記Cのプログラムを、Delphiに変更したものです。
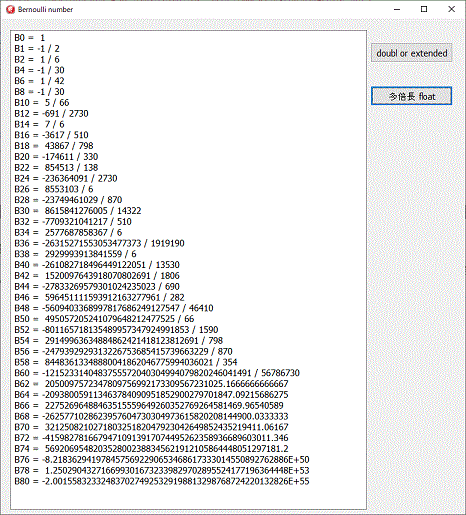多倍長のプログラムを作成する前に、浮動小数点Extendedでプログラムを作成し、それから多倍長のプログラムに変換しています。
Extendedでも、６４bitモードでコンパイルするとDoubleでの精度となります。
多倍長の組み込みは MPArithからmparith_2018-11-27.zipをダウンロードして下さい。
Zipファイルを解凍して、解凍したフォルダーにパス(ツール->オプション->Delphiオプション->ライブラリ->ライブラリパス)を追加し、Uses に mp_types, mp_real,
mp_baseを追加すれば使用可能になります。
左図では、B62以降浮動小数点表示となっていますが、
mpf_set_default_decprec(桁数); を使用すると同時に、mpf_decimal_alt(x,
桁数)を変更すれば、大きな値まで、整数計算、分数表示が可能となります。
分数計算時、最大公約数で分母の値を最小値とするため、演算中の分子の値は、表示される値よりも大きくなるので、mpf_set_default_decprec(桁数)は、表示する桁数よりも大きな値を指定する必要があります。
ダウンロード出来るプログラムは修正していないので、必要であれば自分で修正してください。
演算速度は、64ビットの方が圧倒的に早いです。
TForm1.FormCreate(Sender: TObject);
var
tmp: extended;
MP_tmp: mp_float;
begin
mpf_set_default_decprec(150);
// 演算有効桁数指定
mpf_init(MP_EPSILON);
mpf_init(MP_tmp);
memo1.lines.append('B' + inttostr(m) + estr + string(mpf_decimal_alt(b1,
100))
プログラム
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons;
type
TForm1 = class(TForm)
BitBtn1: TBitBtn;
Memo1: TMemo;
BitBtn2: TBitBtn;
procedure BitBtn1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure FormDestroy(Sender: TObject);
procedure BitBtn2Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses mp_real, mp_types, mp_base;
var
EPSILON : extended;
MP_EPSILON : mp_float;
// 浮動小数点の剰余
function fmod(x, y: extended): extended;
var
tmp: extended;
n : integer;
begin
tmp := x / y;
n := trunc(tmp);
result := x - y * n;
end;
// 最大公約数 ユークリッドの互除法
function gcd(x, y: extended): extended;
var
t : extended;
begin
while y <> 0 do begin
t := fmod(x, y);
x := y;
y := t;
end;
result := x;
end;
// ベルヌーイ数計算 普通精度計算
// t[]は分子の値
// qは分母の値
procedure TForm1.BitBtn1Click(Sender: TObject);
const
N = 50;
var
i, m : integer;
q, b1, b2, d, invE: extended;
t: array of extended;
estr : string;
begin
memo1.Clear;
{$IFDEF CPUX64} // プラットフォーム64ビット
begin // double 計算精度15桁
memo1.Lines.Add('CPUX64モード 演算精度 double');
end;
{$ENDIF CPUX64}
{$IFDEF CPUX86} // プラットフォーム32ビット
begin // extended 計算精度19桁
memo1.Lines.Add('CPUX86モード 演算精度 extended');
end;
{$ENDIF CPUX86}
invE := 1 / EPSILON; // 浮動小数点 小数点表示にならない最大値値
// B0,B1
m := 0;
b1 := 1;
memo1.lines.append('B' + inttostr(m) + ' = ' + floatTostr(b1));
m := 1;
b1 := -1;
b2 := 2;
memo1.lines.append('B' + inttostr(m) + ' = ' + floatTostr(b1) + ' / ' + floatTostr(b2));
// B2～
setlength(t, N + 1); // 配列確保 分子の計算に使用 配列全てゼロ
q := 1; // 分母初期値
t[1] := 1; // 分子初期値
for m := 2 to N do begin
for i := 1 to m - 1 do t[i - 1] := i * t[i]; // 分子計算
t[m - 1] := 0; // 〃
for i := m downto 2 do t[i] := t[i] + t[i - 2]; // 〃
if m mod 2 = 0 then begin // 偶数ベルヌーイNoなら
b1 := m * t[0]; // 分子
q := q * 4; // 分母計算
b2 := q * (q - 1); // 分母
if m mod 4 = 0 then begin // ベルヌーイ数がマイナスになるベルヌーイNo
estr := ' = ';
b1 := -b1;
end
else estr := ' = ';
if (abs(b1) < invE) and (b2 < invE) then begin // 小数部が無かったら分数表示
d := gcd(abs(b1), b2); // 最大公約数
b1 := b1 / d;
b2 := b2 / d;
memo1.lines.append('B' + inttostr(m) + estr + floatTostr(b1) + ' / ' + floatTostr(b2));
end
else // 小数部があったら小数点表示
memo1.lines.append('B' + inttostr(m) + estr + floatTostr(b1 / b2));
end;
end;
end;
//------------------------------------------------------------------------------
// 浮動小数点の剰余 多倍長計算
procedure Mp_fmod(x, y: mp_float; var ans: mp_float);
var
tmp, tmp0: mp_float;
n : mp_int;
begin
mpf_init2(tmp, tmp0);
mp_init(n);
mpf_div(x, y, tmp);
mpf_trunc(tmp, n);
mpf_mul_mpi(y, n, tmp0);
mpf_sub(x, tmp0, ans);
mp_clear(n);
mpf_clear2(tmp, tmp0);
end;
// 最大公約数 多倍長計算 ユークリッドの互除法
procedure MP_gcd(a, b: mp_float; var ans: mp_float);
var
t: mp_float;
x, y: mp_float;
begin
mpf_init3(t, x, y);
mpf_copy(a, x); // aの値が変わらないようにコピーして使用
mpf_copy(b, y); // bの値が変わらないようにコピーして使用
repeat
Mp_fmod(x, y, t);
mpf_copy(y, x);
mpf_copy(t, y);
until s_mpf_is0(y);
mpf_copy(x, ans);
mpf_clear3(t, x, y);
end;
// ベルヌーイ数計算 多倍長計算
procedure TForm1.BitBtn2Click(Sender: TObject);
const
N = 80;
var
i, m : integer;
q, b1, b2, d, tmp, invE: mp_float;
t: array[0..N] of mp_float;
estr : string;
begin
mpf_init5(q, b1, b2, d, tmp);
mpf_init(invE);
for i := 0 to N do mpf_init(t[i]);
memo1.Clear;
mpf_inv(MP_EPSILON, invE);
m := 0;
mpf_set1(b1);
memo1.lines.append('B' + inttostr(m) + ' = ' + string(mpf_decimal_alt(b1, 50)));
m := 1;
mpf_set_int(b2, 2);
mpf_chs(b1, b1);
memo1.lines.append('B' + inttostr(m) + ' = ' + string(mpf_decimal_alt(b1, 50))
+ ' / ' + string(mpf_decimal_alt(b2, 50)));
mpf_set1(q);
mpf_set1(t[1]);
for m := 2 to N do begin
for i := 1 to m - 1 do mpf_mul_int(t[i], i, t[i - 1]);
mpf_set0(t[m - 1]);
for i := m downto 2 do mpf_add(t[i], t[i - 2], t[i]);
if m mod 2 = 0 then begin
mpf_mul_int(q, 4, q);
mpf_mul_int(t[0], m, b1);
mpf_sub_int(q, 1, tmp);
mpf_mul(q, tmp, b2);
mpf_copy(b1, tmp);
if m mod 4 = 0 then begin
estr := ' = ';
mpf_chs(b1, b1);
end
else estr := ' = ';
if mpf_is_lt(tmp, invE) and mpf_is_lt(b2, invE) then begin
Mp_gcd(tmp, b2, d);
mpf_div(b1, d, b1);
mpf_div(b2, d, b2);
memo1.lines.append('B' + inttostr(m) + estr + string(mpf_decimal_alt(b1, 50))
+ ' / ' + string(mpf_decimal_alt(b2, 50)));
end
else begin
mpf_div(b1, b2, tmp);
memo1.lines.append('B' + inttostr(m) + estr + string(mpf_decimal_alt(tmp, 50)));
end;
end;
end;
for i := 0 to N do mpf_clear(t[i]);
mpf_clear(invE);
mpf_clear5(q, b1, b2, d, tmp);
end;
//------------------------------------------------------------------------------
procedure TForm1.FormCreate(Sender: TObject);
var
tmp: extended;
MP_tmp: mp_float;
begin
mpf_set_default_decprec(100); // 演算桁数指定
mpf_init(MP_EPSILON);
mpf_init(MP_tmp);
EPSILON := 1;
repeat
tmp := 1;
EPSILON := EPSILON / 2;
tmp := tmp + EPSILON;
until tmp = 1;
EPSILON := EPSILON * 2;
mpf_set1(MP_EPSILON);
repeat
mpf_set1(MP_tmp);
mpf_div_int(MP_EPSILON, 2, MP_EPSILON);
mpf_add(MP_tmp, MP_EPSILON, MP_tmp);
until mpf_is1a(MP_tmp);
mpf_mul_int(MP_EPSILON, 2, MP_EPSILON);
memo1.Clear;
memo1.Lines.Append('EPSIRON = ' + floatTostr(EPSILON));
memo1.Lines.Append('MP_EPSIRON = ' + string(mpf_decimal_alt(MP_EPSILON, 100)));
memo1.Lines.Append('MP_tmp = ' + string(mpf_decimal_alt(MP_tmp, 80)));
mpf_clear(MP_tmp);
end;
procedure TForm1.FormDestroy(Sender: TObject);
begin
mpf_clear(MP_EPSILON);
end;
end.
Bernoulli_number_float.zip
各種プログラム計算例に戻る