ベルヌーイ数 その３
ベルヌーイ数 その２ のプログラムを整数演算にし、全て分数表示をするようにしてみました。
多倍長integerに関しては、浮動小数点の表示も行いますが、ベルヌーイNoが大きいと、値が大きすぎて通常の計算には利用が難しくなります。
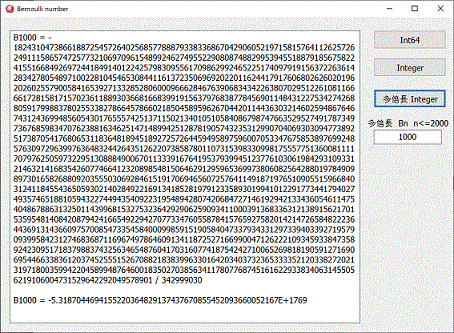多倍長のintegerは、bigintegerなので、大きい桁数の演算が出来ます。
多倍長の演算の組み込みは、ベルヌーイ数 その２を参照してください。
計算は、B2000迄指定できますが、プログラムを変更すれば、もっと大きな値でも計算は可能です。
計算結果が分数で表示されますが、分数のまゝでは、利用できないので、浮動小数点表示もされます。
B1の値は、－1/2とされていることが多いのですが、B1の値は、ベルヌーイ数算出の元の方程式によって＋1/2の値となることがあるので、現在では、±1/2と表記さることが多くなっています。
プログラム
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons;
type
TForm1 = class(TForm)
BitBtn1: TBitBtn;
Memo1: TMemo;
BitBtn2: TBitBtn;
BitBtn3: TBitBtn;
LabeledEdit1: TLabeledEdit;
procedure BitBtn1Click(Sender: TObject);
procedure BitBtn2Click(Sender: TObject);
procedure BitBtn3Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses mp_base, mp_types, mp_real;
// 最大公約数 ユークリッドの互除法 int64
function gcd_int64(x, y: int64): int64;
var
t : int64;
begin
while y <> 0 do begin
t := x mod y;
x := y;
y := t;
end;
result := x;
end;
// ベルヌーイ数計算 1nt64 64ビット
// t[]は分子の値
// qは分母の値
procedure TForm1.BitBtn1Click(Sender: TObject);
const
N = 26;
var
i, m : integer;
q, b1, b2, d: int64;
c1, c2 : int64;
t: array of int64;
estr : string;
begin
memo1.Clear;
setlength(t, N + 1); // 配列確保 配列全て0(ゼロ)
// B0,B1
m := 0;
b1 := 1;
memo1.lines.append('B' + inttostr(m) + ' = ' + floatTostr(b1));
m := 1;
// b1 := -1;
b2 := 2;
memo1.lines.append('B' + inttostr(m) + ' =±' + floatTostr(b1) + ' / ' + floatTostr(b2));
// B2～
q := 1; // 分母計算初期値
t[1] := 1; // 分子計算初期値
for m := 2 to N do begin
for i := 1 to m - 1 do t[i - 1] := i * t[i]; // 分子計算
t[m - 1] := 0; // 〃
for i := m downto 2 do t[i] := t[i] + t[i - 2]; // 〃
if m mod 2 = 0 then begin // 偶数ベルヌーイNoなら
q := q * 4; // 分母計算
b1 := m * t[0]; // 分子
b2 := q * (q - 1); // 分母
c1 := b1 div m; // b1 オーバーフロー確認用
c2 := b2 div (q - 1); // b2 オーバーフロー確認用
if (c1 = t[0]) and (c2 = q) then begin // オーバーフローが無かったら
d := gcd_int64(b1, b2); // 最大公約数
b1 := b1 div d;
b2 := b2 div d;
if m mod 4 = 0 then begin // 4の倍数のベルヌーイNoは負数
estr := ' = ';
b1 := -b1;
end
else estr := ' = ';
memo1.lines.append('B' + inttostr(m) + estr + intTostr(b1) + ' / ' + intTostr(b2));
end
else break;
end;
end;
end;
// 最大公約数 ユークリッドの互除法 integer
function gcd_integer(x, y: integer): integer;
var
t : integer;
begin
while y <> 0 do begin
t := x mod y;
x := y;
y := t;
end;
result := x;
end;
// integer 32ビット整数計算
procedure TForm1.BitBtn2Click(Sender: TObject);
const
N = 16;
var
i, m : integer;
q, b1, b2, d: integer;
c1, c2 : integer;
t: array of integer;
estr : string;
begin
memo1.Clear;
setlength(t, N + 1); // 配列確保 配列全て0(ゼロ)
// B0,B1
m := 0;
b1 := 1;
memo1.lines.append('B' + inttostr(m) + ' = ' + floatTostr(b1));
m := 1;
// b1 := -1;
b2 := 2;
memo1.lines.append('B' + inttostr(m) + ' =±' + floatTostr(b1) + ' / ' + floatTostr(b2));
// B2～
q := 1; // 分母計算初期値
t[1] := 1; // 分子計算初期値
for m := 2 to N do begin
for i := 1 to m - 1 do t[i - 1] := i * t[i]; // 分子計算
t[m - 1] := 0; // 〃
for i := m downto 2 do t[i] := t[i] + t[i - 2]; // 〃
if m mod 2 = 0 then begin // 偶数ベルヌーイNoなら
q := q * 4; // 分母計算
b1 := m * t[0]; // 分子
b2 := q * (q - 1); // 分母
c1 := b1 div m; // b1 オーバーフロー確認用
c2 := b2 div (q - 1); // b2 オーバーフロー確認用
if (c1 = t[0]) and (c2 = q) then begin // オーバーフローが無かったら
d := gcd_integer(b1, b2); // 最大公約数
b1 := b1 div d;
b2 := b2 div d;
if m mod 4 = 0 then begin // 4の倍数のベルヌーイNoは負数
estr := ' = ';
b1 := -b1;
end
else estr := ' = ';
memo1.lines.append('B' + inttostr(m) + estr + intTostr(b1) + ' / ' + intTostr(b2));
end
else break;
end;
end;
end;
// 最大公約数 ユークリッドの互除法 多倍長整数
procedure gcd_mp_int(a, b: mp_int; var ans: mp_int);
var
t : mp_int;
x, y : mp_int;
begin
mp_init3(t, x, y);
mp_copy(a, x);
mp_copy(b, y);
repeat
mp_mod(x, y, t);
mp_copy(y, x);
mp_copy(t, y);
until s_mp_is_le0(y);
mp_copy(x, ans);
mp_clear3(t, x, y);
end;
// ベルヌーイ数 多倍長整数演算
procedure TForm1.BitBtn3Click(Sender: TObject);
var
i, m, N: integer;
q, b1, b2, d, tmp, invE: mp_int;
c1, c2, qm1: mp_int;
b1f, b2f, bnf: mp_float;
t: array of mp_int;
estr : string;
begin
// N := 2000;
val(labelededit1.Text, N, i);
if i <> 0 then begin
Memo1.Clear;
memo1.Text := '多倍長のBnのNの値に間違いがありまます。';
exit;
end;
N := abs(N);
if N > 2000 then begin
Memo1.Clear;
memo1.Text := '多倍長のNの値は2000迄にしてください。';
exit;
end;
mp_init5(q, b1, b2, d, tmp);
mp_init(invE);
mp_init3(c1, c2, qm1);
mpf_init3(b1f, b2f, bnf);
setlength(t, N + 1);
for i := 0 to N do mp_init(t[i]);
memo1.Clear;
mp_set1(b1);
// B0 = 1
if N = 0 then begin
m := 0;
memo1.lines.append('B' + inttostr(m) + ' = ' + string(mp_adecimal(b1)));
end;
// B1 = -1 / 2
if N = 1 then begin
m := 1;
mp_set_int(b2, 2);
// mp_chs(b1, b1);
memo1.lines.append('B' + inttostr(m) + ' =±' + string(mp_adecimal(b1))
+ ' / ' + string(mp_adecimal(b2)));
mpf_set_mpi(b1f, b1); // 浮動小数点変換 b1->b1f
mpf_set_mpi(b2f, b2); // 浮動小数点変換 b2->b2f
mpf_div(b1f, b2f, bnf); // bnf = b1f/b2f
memo1.lines.append('');
memo1.lines.append('B' + inttostr(m) + ' =±' + string(mpf_adecimal_alt(bnf, 50)));
end;
// B2～
if N >= 2 then begin
if N mod 2 <> 0 then memo1.lines.append('B' + inttostr(N) + ' = 0')
else begin
mp_set1(q); // 分母計算初期値
mp_set1(t[1]); // 分子計算初期値
for m := 2 to N do begin
for i := 1 to m - 1 do mp_mul_int(t[i], i, t[i - 1]); // 分子計算
mp_set_int(t[m - 1], 0); // 〃
for i := m downto 2 do mp_add(t[i], t[i - 2], t[i]); // 〃
if m mod 2 = 0 then begin // 偶数ベルヌーイNoなら
mp_mul_int(q, 4, q); // 分母計算
if m = N then begin // 指定ベリヌーイ数になったら
mp_mul_int(t[0], m, b1); // b1 = t[0] * m
mp_sub_int(q, 1, qm1); // qm1 = q - 1
mp_mul(q, qm1, b2); // b2 = q * (q - 1)
mp_set_int(tmp, m);
mp_div(b1, tmp, c1); // c1 = b1 / m
mp_div(b2, qm1, c2); // c2 = b2 / (q - 1)
if mp_is_eq(t[0], c1) and mp_is_eq(c2, q) then begin // オーバーフローが無かったら
gcd_mp_int(b1, b2, d); // d = 最大公約数
if m mod 4 = 0 then begin // Bnが4の倍数なら
estr := ' = ';
mp_chs(b1, b1); // b1の符号反転
end
else estr := ' = ';
mp_div(b1, d, b1); // b1 = b1 / d
mp_div(b2, d, b2); // b2 = b2 / d
memo1.lines.append('B' + inttostr(m) + estr + string(mp_adecimal(b1))
+ ' / ' + string(mp_adecimal(b2)));
mpf_set_mpi(b1f, b1); // 浮動小数点変換 b1->b1f
mpf_set_mpi(b2f, b2); // 浮動小数点変換 b2->b2f
mpf_div(b1f, b2f, bnf); // bnf = b1f/b2f
memo1.lines.append('');
memo1.lines.append('B' + inttostr(m) + estr + string(mpf_adecimal_alt(bnf, 50)));
end
else break;
end;
end;
end;
end;
end;
for i := 0 to N do mp_clear(t[i]);
mpf_clear3(b1f, b2f, bnf);
mp_clear3(c1, c2, qm1);
mp_clear(invE);
mp_clear5(q, b1, b2, d, tmp);
end;
end.
Bernoulli_number_integer.zip
各種プログラム計算例に戻る