ねじ歯車計算

　ねじ歯車の計算です。
計算の詳細については参考書を参照して下さい。適当な参考書が見つからない場合は、小原歯車のホームページで、資料を公開しているのでそちらを参照して下さい。
インターネットで"小原歯車"の検索を実行すれば直ぐに見つかるでしょう、初心者用から、設計者用まで、可なり詳しく紹介しています。
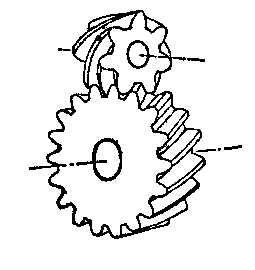
　ねじ歯車は、ハスバ歯車を二個組み合わせて、食い違い軸の駆動伝達を出来る様にしています。
軸角９０°が一般的ですが角度を自由に取ることも可能です。
９０°の物は、汎用品として市販されていますが、ギヤ比は限られています、このプログラムは、軸角を自由に設定するためのプログラムです。
転位したハスバ歯車も使用可能です。
　計算出来るのは、軸間距離と駆動軸と従動軸の角度を指定した場合の各々のネジリ角です。
又、それぞれのギヤのデーターを入力する事により、軸角を求める事が出来ます。
円筒ウォームとして使用する為、駆動側の歯数を一枚にして計算することも可能になっています。
　片方の歯車を既製品として、もう片方のギヤを求める計算はありません、特に転位したギヤを使用する場合は計算が複雑になるので、プログラムのルーチンを追加してください。
　歯数が少なくて切り下げが発生する場合、転位をすることも可能ですが、ハスバ歯車の様に自動的に転位量を計算するようにはなっていません。
本プログラムを修正すれば、切り下げが発生した時、自動的に最小のプラス転位量を求める事が出来る様になるでしょう。

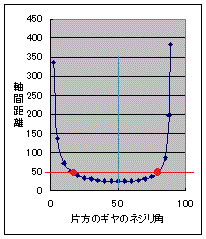　左図は、ネジリ角によって軸間がどの様に変化するかの一例のグラフです。
ある角度左図では約５０°になってますが、その角度で軸間が最小となり、それより小さくても、大きくても軸間は広がります。
軸間を指定した場合、軸間最小値より小さい値を指定すると、解はありません。最小値と同じ値を指定すると解は一つとなります。最小値より大きい値を指定すると、解は二つ存在することになります。
本プログラムでは、二つ存在する場合、どちらにするか選択するようになっています。

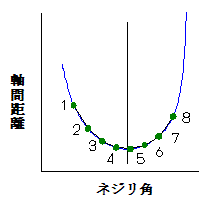　軸間指定でネジリ角を求める場合、まず最初に指定された軸間より大きな値になる角度から計算を始めます。
　　片方の歯車に、
　　　　　　ネジリ角　β１　１°を与えると
　　反対側のネジリ角　β２　単純には
　　　　　軸角　Σ　－　β1　となりますが、
転位がある場合は、平行軸ハスバ歯車と違って、軸角が変化しますので注意が必要です。
ネジリ角β１　を、少しずつ変化させて計算しますが、その変化量を⊿βとして、左図の図中番号１，２，３，４，５，６と計算し、５から６になった時軸間距離が最小値を越えたことになります。
最小値を越えたら、計算を二つ前に戻し、⊿βをもっと小さい値にして４の時点から計算を再開し、⊿βが十分に小さく（誤差として無視できる値）なった時を軸間最短距離とします。
二つ前に戻すのは最小値を超えた判定は、前の値より、大きくなったかどうかで判定しますが、前の値が既に最小値を越えてしまうことがあるからです。これで、最短距離が求まったので、次は、指定された軸間距離の計算となります、計算に先立って、解が無いのか、一つなのか、二つなのかを判定し、今度は指定された距離に対するネジリ角を求めることになりますが、指定値に対する判定の符号、軸間が小さくなっていく方向なのか、大きくなっていく方向なのかに注意を払う必要があります。

後の計算は、ハスバ歯車と同じですが、伝達効率、強度計算は、歯のかみ合い方が違うので、少し違った計算となっています。
本プログラムで、平行軸の計算も出来ますが、軸角０度の場合は、ハスバ歯車の計算を使用して下さい。