懸垂線の長さ指定計算 DKA法使用
懸垂線の長さと支持位置を指定しカテナリー数Cを求めて、弛みを計算します。
此処では、ニュートン法での収束ではなく、冪級数展開した値を、DKA法で解放します。
ニュートン法の時は、近似値としてC4迄しましたが、此処ではC30位まで展開します。
求めるカテナリー数が大きくなると、オーバーフローするのでその時は、冪級数展開の次数を小さくします。
指定した長さが、支持間の直線での長さに近づくとカテナリー数Cが急激に大きくなり、同じ長さで∞となります。
精度は、次数が大きい方が高くなりますので、適当に調整します。
直線距離に対して、上から12桁目ぐらいが大きくなっていないと、計算結果が出たとしても、誤差が大きくなります。
Doubleで計算していますが、精度が15桁ぐらいだからです。
カテナリー数が非常に大きい場合で、精度を高くする為には、多倍長での演算が必用です。
オーバーフローギリギリ迄次数を大きくすればカテナリー数Cの値の誤差は、懸垂線の長さ指定のニュートン法と同じくらいまで得ることができます。
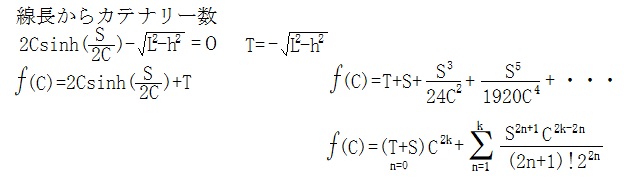 冪級数展開した値にC2k-2nを掛けてCの級数にします。
冪級数展開した値にC2k-2nを掛けてCの級数にします。
プログラムの長さも、計算時間もニュートン法の方が短くなります。
DKA法でも、計算が出来る参考のプログラムです。
冪級数展開では偶数次数項のみ値が割り振られるので、奇数次数項はゼロにします。
DKA法で解析された値で虚数部がゼロに近い値がカテナリー数Cとなり、値は+と-の二つとなりますが、絶対値は同じになります。
DKA法の収束計算で、指定された値まで収束しない場合は、最大ループ数迄、計算が続行されます。
計算された値には、何も問題はありません、単に計算終了に時間が掛かるだけです。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls,
VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs,
VCLTee.Chart;
type
TForm1 = class(TForm)
Memo1: TMemo;
Panel1: TPanel;
h_Edit: TLabeledEdit;
S_Edit: TLabeledEdit;
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
Button1: TButton;
CheckBox1: TCheckBox;
Series3: TLineSeries;
Series4: TPointSeries;
Length_Edit: TLabeledEdit;
divide_Edit: TLabeledEdit;
Series5: TPointSeries;
Timer1: TTimer;
Button2: TButton;
deg_Edit: TLabeledEdit;
CheckBox2: TCheckBox;
procedure Button1Click(Sender: TObject);
procedure Timer1Timer(Sender: TObject);
procedure Button2Click(Sender: TObject);
private
{ Private 宣言 }
function datainput: boolean;
procedure Drawing;
procedure CalcXY;
function dataset(n: integer; var d: array of double): boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses
system.Math;
var
S : double; // 支持間 m
h : double; // 高低差 m
B : integer; // 分割数
C : double; // カテナリー数
d : double; // 弛度 m
m : double; // 最大たるみ位置 m
dm :double; // 最大たるみ位置 弛度 m
x : double; // 斜弛度地点までの距離 m
L : double; // 線実長
deg : integer; // DKA法次数
No : integer; // 自動計算線長
Tf : boolean = false; // 自動計算タイマー停止フラグ
// 入力処理
function TForm1.datainput: boolean;
var
ch : integer;
Lmin : double;
mstr : string;
begin
result := false;
val(S_edit.Text, S, ch);
if ch <> 0 then begin
application.MessageBox('支持間距離に間違いがあります。','注意',0);
exit;
end;
val(h_edit.Text, h, ch);
if ch <> 0 then begin
application.MessageBox('高低差に間違いがあります。','注意',0);
exit;
end;
Lmin := sqrt(h * h + S * s);
val(Length_edit.Text, L, ch);
if ch <> 0 then begin
application.MessageBox('線の長さに間違いがあります。','注意',0);
exit;
end;
if Lmin >= L then begin
mstr := '最小値は' + floatTostr(Lmin) + 'です。';
application.MessageBox(Pchar(mstr),'注意',0);
exit;
end;
val(divide_edit.Text, B, ch);
if ch <> 0 then begin
application.MessageBox('分割数に間違いがあります。','注意',0);
exit;
end;
if B <= 0 then begin
application.MessageBox('分割数は1以上にして下さい。','注意',0);
exit;
end;
val(deg_edit.Text, deg, ch);
if ch <> 0 then begin
application.MessageBox('次数の値に間違いがあります。','注意',0);
exit;
end;
if deg < 4 then begin
application.MessageBox('次数が小さすぎます4以上にして下さい。','注意',0);
exit;
end;
if 40 < deg then begin
application.MessageBox('次数が大きすぎます40以下にして下さい。','注意',0);
exit;
end;
if deg mod 2 <> 0 then begin
application.MessageBox('次数の値は偶数にして下さい。','注意',0);
exit;
end;
result := true;
end;
// Durand Kerner Aberth algorithm
function dka(a : array of double; var cr, ci: array of double; n: integer): boolean;
var
r, r0, t : double;
e, f1, f2, w1, w2 : double;
p1, p2, a1, a2, norm: double;
i, j, L: integer;
ca : array of double;
zc : double;
StrText : string;
eps : double;
begin
result := true;
setlength(ca, n + 1);
for i := 0 to n do ca[i] := a[i];
zc := - ca[n-1] / n;
for i := 1 to n do
for j := n downto i do
ca[j-1] := ca[j-1] + ca[j] * zc;
r := 0;
for i := 0 to n - 1 do begin
r0 := power(n * abs(ca[i]), 1/(n-i));
if r < r0 then r := r0;
end;
Form1.Memo1.Lines.Add('R = ' + floatTostr(R));
eps := 1E-15 * r; // 半径で収束判定値調整
for i := 1 to n do begin // 半径rの円に等間隔に配置する
t := 2 * PI / n * (i - 3.0 / 4.0);
cr[i-1] := -a[n-1] / n + r * cos(t); // アーバスの初期値
ci[i-1] := r * sin(t);
end;
L := 0;
e := 0;
try
repeat
eback := e;
e := 0;
for i := 0 to n -1 do begin
f1 := 1; // 分子 f(zi)、実部=f1,虚部=f2
f2 := 0; // ※a[n]=1
for j := n-1 downto 0 do begin // ホーナー法 f(z)=( … ((z+a[n-1])*z+a[n-2])*z+a[n-3])* … +a[1])*z+a[0]
w1 := f1 * cr[i] - f2 * ci[i]; // f*z=(f1+i*f2)*(x1+i*x2)=(f1*x1-f2*x2)+i*(f1*x2+f2*x1)
w2 := f2 * cr[i] + f1 * ci[i];
f1 := w1 + a[j]; // f=z+a[j]
f2 := w2;
end;
p1 := 1; // 分母 Π[j=1,N,i≠j](zi-zj)、実部=p1,虚部=p2
p2 := 0;
for j := 0 to n - 1 do begin
if j <> i then begin
w1 := p1 * (cr[i] - cr[j]) - p2 * (ci[i] - ci[j]); // p*(zi-zj)
w2 := p1 * (ci[i] - ci[j]) + p2 * (cr[i] - cr[j]);
p1 := w1; // p=(zi-zj)
p2 := w2;
end;
end;
t := p1 * p1 + p2 * p2; // 分子÷分母 (f1+i*f2)/(p1+i*p2)=(f1+i*f2)(p1-i*p2)/(p1*p1+p2*p2)
if t = 0 then begin
application.MessageBox('0では割れません。(DKAルーチン)', '注意', 0);
result := false;
exit;
end;
a1 := (f1 * p1 + f2 * p2) / t;
a2 := (f2 * p1 - f1 * p2) / t;
norm :=sqrt(a1 * a1 + a2 * a2);
if e < norm then e := norm; // 最大値
cr[i] := cr[i] - a1; // k回目の近似根 zi[k+1]=zi[k]-f(zi[k])/Π[j=1,N,i≠j](zi[k]-zj[k])
ci[i] := ci[i] - a2;
end;
inc(L);
until (e < eps) or (L > 400);
except
on E: Exception do begin
StrText := E.ClassName + sLineBreak + E.Message;
StrText := StrText + #13#10 + 'DKA法計算ルーチン';
StrText := StrText + sLineBreak + 'オーバーフローだったら次数を下げて計算してみてください。';
Application.MessageBox(PChar(StrText), '情報', MB_ICONINFORMATION);
Form1.Timer1.Enabled := False;
Tf := False;
result := False;
end;
end;
Form1.Memo1.Lines.Add('DKA法 Loop = ' + intTostr(L))
end;
// sinh 値用N次元データー作成
function TForm1.dataset(n: integer; var d: array of double): boolean;
var
T : double;
m : integer;
i : integer;
StrText : string;
function factorial(n: integer): double; // n!
var
j : integer;
begin
result := 1;
for j := 2 to n do result := result * j;
end;
begin
result := true;
for i := 0 to n do d[i] := 0; // 配列クリア
T := sqrt(L * L - h * h);
d[n] := S - T; // 次数n
try
for i := 1 to n div 2 do begin
m := n - 2 * i; // 次数m n-2 -> 0 偶数次数
d[m] := power(S, 2 * i + 1) / factorial(2 * i + 1) / power(2, 2 * i);
end;
except
on E: Exception do begin
StrText := E.ClassName + sLineBreak + E.Message;
StrText := StrText + #13#10 + '配列のデーター作成ルーチン';
Application.MessageBox(PChar(StrText), '情報', MB_ICONINFORMATION);
Tf := False;
Timer1.Enabled := False;
result := false;;
end;
end;
end;
// 懸垂線作図
// 低い方の支持位置基準
procedure TForm1.Drawing;
const
KN = 500;
var
xn : double;
xd, dx : double;
y : double;
i : integer;
begin
dx := S / KN;
// 懸垂線作図
for i := 0 to KN do begin
xn := i * dx; // 計算位置
xd := abs(xn - m); // 最大弛み位置からの距離
y := C * (cosh(xd / C) - 1) - dm; // 高さ 低い方の支持位置を基準として計算
Series1.AddXY(xn, y);
end;
// 斜弛み位置通過接線
Series3.AddXY(0, 0 - d); // 斜弛み位置通過傾斜線 低い方
Series3.AddXY(S, h - d); // 斜弛み位置通過傾斜線 高い方
// 支持位置 斜弛度地点 丸表示
Series4.AddXY(0, 0); // 低い方の支持位置
y := h / S * x - d; // 斜弛度y座標
Series4.AddXY(x, y); // 斜弛度xy
Series4.AddXY(S, h); // 高い方の支持位置
end;
// 懸垂線等分割位置の計算
procedure TForm1.CalcXY;
var
Ls : double;
Sb : double;
xs, y : double;
n : integer;
begin
for n := 1 to B - 1 do begin
Ls := L / B * n; // 線の長さ
Sb := C * (arcSinh(Ls / C - sinh(m / C))) + m; // 仮の支持位置
xs := Sb - m; // 撓み計算位置
y := C * (cosh(xs / C) - 1) - dm; // 高さ 低い方の支持位置を基準として計算
Series5.AddXY(Sb, y); // 分割位置
end;
end;
// 懸垂線計算の実行 線長からカテナリー数を求めます
// その後グラフ作成
procedure TForm1.Button1Click(Sender: TObject);
var
s1 : double;
lmin, lmax : double;
bmin, bmax : double;
mg : double;
ab : array of double;
cr : array of double;
ci : array of double;
n, i, j : integer;
li : int64;
StrText, scou : string;
fd : double;
ch : integer;
cn : array of double;
Lc : double;
Lm : double;
// 丸め処理
procedure roundfd(var d: double);
begin
if abs(d) < 1E5 then begin // 0.00001 以下の場合
li := round(d * 1E8); // 小数点8桁以下丸め
d := li / 1E8;
end;
end;
begin
Timer1.Enabled := False;
if not datainput then exit;
button1.Enabled := False;
n := deg;
// 次数で配列の確保
setlength(ab, n + 1);
setlength(cr, n);
setlength(ci, n);
setlength(cn, 2);
// 配列にデーターセット
if not dataset(n, ab) then begin
Button1.Enabled := true;
timer1.Enabled := False;
Tf := False;
exit;
end;
j := 0;
// 配列先頭の値を1に設定
try
for i := n-1 downto 0 do begin
ab[i] := ab[i] / ab[n];
end;
ab[n] := 1;
except
on E: Exception do begin
StrText := E.ClassName + sLineBreak + E.Message;
StrText := StrText + #13#10 + '配列の先頭を1にする処理';
j := 1; // 演算エラーフラグセット
end;
end;
if j = 1 then begin // 演算エラーがあったら
Application.MessageBox(PChar(StrText), '情報', MB_ICONINFORMATION);
Button1.Enabled := true;
timer1.Enabled := False;
Tf := False;
exit;
end;
memo1.Clear;
Lm := (L - sqrt(S * S + h * h)) / L;
if Lm <= 1E-11 then
memo1.Lines.Add('指定長さが直線距離に近すぎ計算誤差が大きくなります。');
// 配列データー表示
if checkbox2.Checked then begin
memo1.Lines.Add('配列データー n 奇数次数はゼロ');
memo1.Lines.Add('次数 n= ' + intTostr(n));
for i := n downto 0 do begin
if i mod 2 = 0 then begin
scou := 'n' + inttostr(i) + '= ' + floatTostr(ab[i]);
memo1.Lines.Add(scou);
end;
end;
end;
// dka法計算 カテナリー数Cの値を求めます
if not dka(ab, cr, ci, n) then begin
Button1.Enabled := true;
timer1.Enabled := False;
Tf := False;
exit;
end;
// dka法 計算結果表示
if Checkbox2.Checked then
for i := 0 to n-1 do begin
fd := cr[i]; // 実数部
roundfd(fd); // 値が小さい場合小数点8桁以下丸め
scou := 'x' + inttostr(i + 1) + '= ' + floatTostr(fd);
ch := length(scou);
ch := 28 - ch;
for j := 0 to ch do scou := scou + ' ';
fd := ci[i]; // 虚数部
roundfd(fd); // 小数点8桁以下丸め
memo1.Lines.Add(scou + floatTostr(fd) + ' i');
end;
// Cの検出 虚数が小さい場所 xが+-の二箇所絶対値は同じ値
j := 0;
for i := 0 to n-1 do begin
if abs(ci[i]) < 1E-8 then begin
fd := cr[i];
if j <= 1 then begin
cn[j] := fd;
end;
inc(j);
end;
end;
if (j = 0) or (j > 2) then begin
if j = 0 then
StrText := 'DKA法演算が収束しませんでした。';
if j > 2 then
StrText := 'DKA法での計算 桁落ちの可能性があります。';
Application.MessageBox(PChar(StrText), '情報', MB_ICONINFORMATION);
Button1.Enabled := true;
timer1.Enabled := False;
Tf := False;
exit;
end;
// 計算結果表示
C := abs(cn[0]); // cn[0]とcn[1]の絶対値は同じ
memo1.Lines.Add('カテナリー数 C= ' + floatTostr(C));
m := S / 2 - C * arcsinh(h / (2 * C * sinh(S / 2 / C)));
memo1.Lines.Add('最大たるみ位置 m= ' + floatTostr(m));
Lc := C * (sinh(m / c) + sinh((S - m) / C));
memo1.Lines.Add('線長計算値 Lc= ' + floatTostr(Lc));
memo1.Lines.Add('線長計算差 dL= ' + floatTostr(L - Lc));
s1 := abs(m * 2);
dm := C * (cosh(s1 / 2 / C) - 1);
memo1.Lines.Add('最大位置 弛度 dm= ' + floatTostr(dm));
x := m + C * arcsinh(h / S);
memo1.Lines.Add('斜弛度位置 x=' + floatTostr(x));
d := x / S * h + C * (cosh(m / C) - cosh(arcsinh(h / S)));
memo1.Lines.Add('斜弛度 d=' + floatTostr(d));
memo1.Lines.Add('直線距離 =' + floatTostr(sqrt(h * h + S * S)));
if h > 0 then begin
lmin := -d;
lmax := h;
end
else begin
lmin := -d + h;
lmax := 0;
end;
bmin := 0;
bmax := S;
// グラフ縦横スケール設定
if bmax > lmax - lmin then begin
mg := (bmax - (lmax - lmin)) / 2;
lmax := lmax + mg;
lmin := lmin - mg;
end
else begin
mg := ((lmax - lmin) - bmax) / 2;
bmin := bmin - mg;
bmax := bmax + mg;
end;
Series1.Clear;
Series2.Clear;
Series3.Clear;
Series4.Clear;
Series5.Clear;
if checkbox1.Checked then begin
Series2.AddXY(bmin, lmax);
Series2.AddXY(bmin, lmin);
Series2.AddXY(bmax, lmin);
end;
application.ProcessMessages;
// グラフ表示
Drawing; // 懸垂線グラフ
CalcXY; // 線長等分割点表示
application.ProcessMessages;
if tf then Timer1.Enabled := True
else button1.Enabled := true;
end;
// テスト計算スタートストップ
procedure TForm1.Button2Click(Sender: TObject);
var
ch : integer;
begin
checkbox2.Checked := false;
divide_Edit.Text := '5';
Timer1.Interval := 20;
if Tf then begin
Tf := False;
timer1.Enabled := False;
Button1.Enabled := True;
end
else begin
val(S_Edit.Text, S, ch);
if ch <> 0 then exit;
val(h_Edit.Text, h, ch);
if ch <> 0 then exit;
timer1.Enabled := True;
Tf := True;
Button1.Enabled := False;
No := round(sqrt(S * S + h * h) + 1); // テスト計算長さ
Length_Edit.Text := intTostr(No);
end;
end;
// テスト計算繰り返しタイマー
procedure TForm1.Timer1Timer(Sender: TObject);
begin
Length_Edit.Text := intTostr(No);
Button1Click(nil);
inc(No);
if No > 500 then No := round(sqrt(S * S + h * h) + 1);
end;
end.
 catenary_DKALength.zip
catenary_DKALength.zip
各種プログラム計算例に戻る
最初に戻る
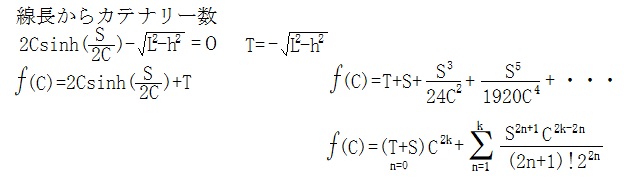 冪級数展開した値にC2k-2nを掛けてCの級数にします。
冪級数展開した値にC2k-2nを掛けてCの級数にします。