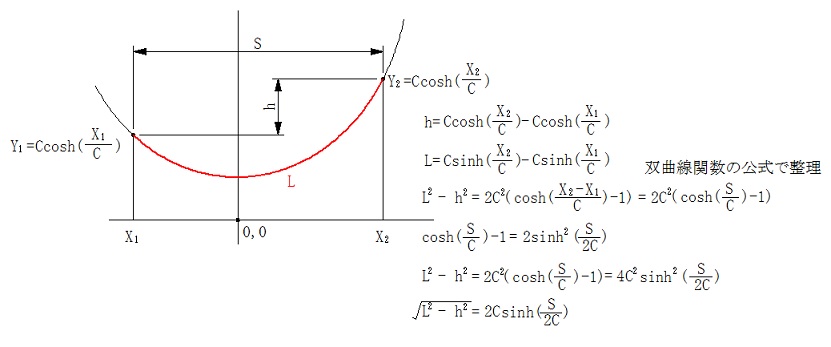
懸垂線の長さ指定
懸垂線の長さを指定して、カテナリー数を求めるプログラムがインターネットにあったので、Delphiで同じプログラムを作成してみました。
線長からカテナリー数を求めることの出来る計算式が必要なので、まずはこれの検討です。
与えられた条件、懸垂線の支持間S、高低差h、線長Lと求めるべきカテナリー数Ｃ からなる方程式を導き出します。
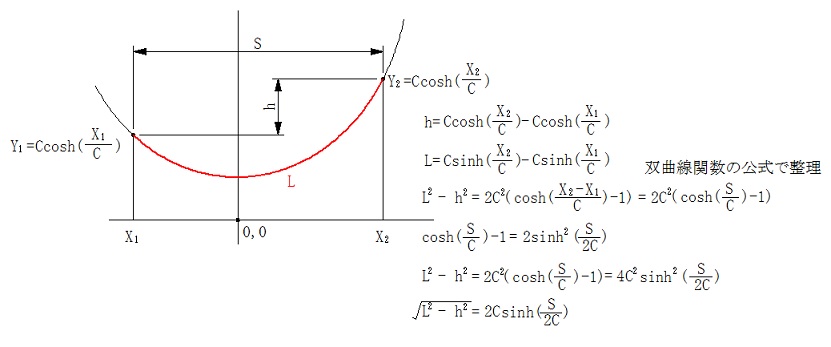
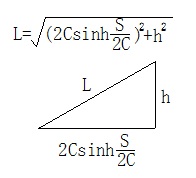詳細は懸垂線、Wikipedia Catenaryを参照してください。
2Csinh(S/(2C))は、懸垂線の左右の支持位置の高さが等しい場合の懸垂線の長さの計算式です。
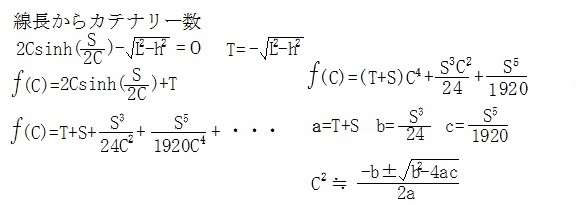Ｌ(線長)、ｈ(高低差)、Ｓ（支持間）は既知数として与えられているので、Cを求める為の式に変形します。
残念ながらＣを求める為の逆関数はありません。
そこでニュートン法を用いて計算をするのですが、近似値を与える必要があります。
近似値を求める為の計算式を作る為、冪級数展開を行います。
展開を分母Ｃ4迄とし、両辺にC4を掛ければ、四次方程式となります。
この四次方程式には、奇数次数項がないので、（Ｃ2）2として二次方程式を解法すれば、カテナリー数Ｃの近似値を得ることが出来ます。
カテナリー数Ｃは、実数のみなので、簡単に近似値を求める事ができます。
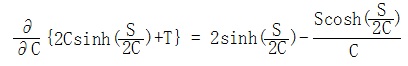
更に、ニュートン法で、指定長に収束する為、微分を行います。
計算回数は増えますが、ニュートン法、近似式を使用しなくても、カテナリー数を求める事は可能です。
長さLは、カテナリー数Ｃに反比例する事と、答えが一つしかない事から、適当なカテナリー数Ｃを与えて長さＬ’を計算し、長かったらカテナリー数Ｃを大きく、短かったらカテナリー数を小さくしてながら収束させれば簡単なプログラムで、カテナリー数を求める事ができます。
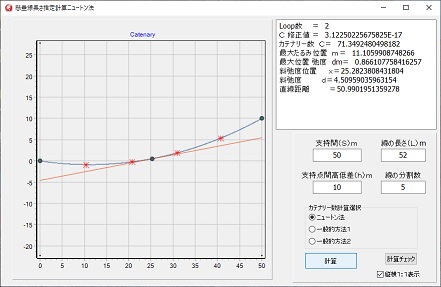左図は、指定長さLのカテナリー数Ｃを求めるのと、長さＬを等分割した場合の実行例です。
インターネットに有ったプログラムにあわせてみました。
ニュートン法を使用しない場合の計算も出来ます。
計算チェックは、指定長さＬを１ずつ長くして、自動計算を行います。
長さが500を超えたら最初の長さに戻ります。
注 指定された長さが、支持間の直線距離にあまりにも近いと、カテナリー数が非常に大きくなり、桁落ちや演算誤差により、計算結果が出たとしても、正しい答えとなりません。
直線距離に対して、値の上の桁から、少なくとも、12桁目位の値が大きくなっている必要があります。
此処のプログラムでは、精度Doubleで有効桁数15桁程度です。
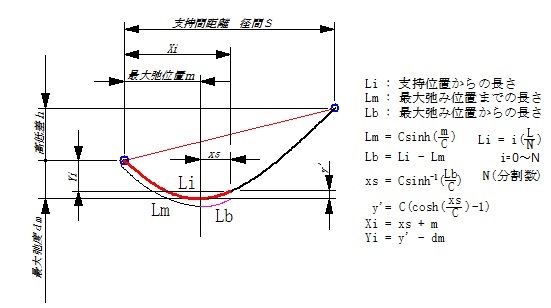
左は、等分割されたカテナリー線の分割位置の座標を計算する計算式です。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls,
VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs,
VCLTee.Chart;
type
TForm1 = class(TForm)
Memo1: TMemo;
Panel1: TPanel;
h_Edit: TLabeledEdit;
S_Edit: TLabeledEdit;
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
Button1: TButton;
CheckBox1: TCheckBox;
Series3: TLineSeries;
Series4: TPointSeries;
Length_Edit: TLabeledEdit;
divide_Edit: TLabeledEdit;
Series5: TPointSeries;
RadioGroup1: TRadioGroup;
Timer1: TTimer;
Button2: TButton;
procedure Button1Click(Sender: TObject);
procedure Timer1Timer(Sender: TObject);
procedure Button2Click(Sender: TObject);
private
{ Private 宣言 }
function datainput: boolean;
procedure Drawing;
procedure Calc;
procedure CalcXY;
procedure Calced;
function f(Ct, S, sL2mh2: double): double;
function dfdx(Ct, S: double): double;
function f_inverse(S, Lh: double): double;
function f_inverse_newton(S, sL2mh2: double): double;
function solve_C(S, h, L: double): double;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses
system.Math;
var
S : double; // 支持間 m
h : double; // 高低差 m
B : integer; // 分割数
C : double; // カテナリー数
d : double; // 弛度 m
m : double; // 最大たるみ位置 m
dm :double; // 最大たるみ位置 弛度 m
x : double; // 斜弛度地点までの距離 m
L : double; // 線実長
No : integer;
Tf : boolean = false;
// 入力処理
function TForm1.datainput: boolean;
var
ch : integer;
Lmin : double;
mstr : string;
begin
result := false;
val(S_edit.Text, S, ch);
if ch <> 0 then begin
application.MessageBox('支持間距離に間違いがあります。','注意',0);
exit;
end;
val(h_edit.Text, h, ch);
if ch <> 0 then begin
application.MessageBox('高低差に間違いがあります。','注意',0);
exit;
end;
Lmin := sqrt(h * h + S * s);
val(Length_edit.Text, L, ch);
if ch <> 0 then begin
application.MessageBox('線の長さに間違いがあります。','注意',0);
exit;
end;
if Lmin >= L then begin
mstr := '最小値は' + floatTostr(Lmin) + 'です。';
application.MessageBox(Pchar(mstr),'注意',0);
exit;
end;
val(divide_edit.Text, B, ch);
if ch <> 0 then begin
application.MessageBox('分割数に間違いがあります。','注意',0);
exit;
end;
if B <= 0 then begin
application.MessageBox('分割数は１以上にして下さい。','注意',0);
exit;
end;
result := true;
end;
// 懸垂線作図
// 低い方の支持位置基準
procedure TForm1.Drawing;
var
xn : double;
xd, dx : double;
y : double;
i : integer;
begin
dx := S / 1000;
// 懸垂線作図
for i := 0 to 1000 do begin
xn := i * dx; // 計算位置
xd := abs(xn - m); // 最大弛み位置からの距離
y := C * (cosh(xd / C) - 1) - dm; // 高さ 低い方の支持位置を基準として計算
Series1.AddXY(xn, y);
end;
// 斜弛み位置通過接線
Series3.AddXY(0, 0 - d); // 斜弛み位置通過傾斜線 低い方
Series3.AddXY(S, h - d); // 斜弛み位置通過傾斜線 高い方
// 支持位置 斜弛度地点 丸表示
Series4.AddXY(0, 0); // 低い方の支持位置
y := h / S * x - d; // 斜弛度y座標
Series4.AddXY(x, y); // 斜弛度xy
Series4.AddXY(S, h); // 高い方の支持位置
end;
// 長さからカテナリー数計算
// 長さ近似値のカテナリー数
procedure TForm1.Calc;
const
KP = 500000; // 最大ループ数
// KP = 100; // 最大ループ数
var
Cd : double;
L0 : double;
Ld : double;
Loop : integer;
eps : double;
begin
eps := 1.0E-15 * L; // 判定値
C := 1; // カテナリー数初期値
Cd := 128; // カテナリー数補助値
Loop := 0; // ループ数 無限ループ対策
repeat
m := S / 2 - C * arcsinh(h / (2 * C * sinh(S / 2 / C))); // 最大弛み位置
L0 := C * (sinh(m / C) + sinh((S - m) / C)); // 仮の長さ計算
Ld := L - L0; // 指定長さとの差計算
if Ld < 0 then C := C + Cd; // 仮の長さが長すぎたら加算
if Ld > 0 then begin // 短かったら
C := C - Cd; // カテナリー数戻し
Cd := Cd / 2; // 補正値二分の一
C := C + Cd; // 補正値加算
end;
inc(Loop); // ループ数インクリメント
until (Cd < eps) or (Loop > KP) or (Ld = 0); // 収束判定
memo1.Lines.Add('Loop数 ＝ ' + intTostr(Loop));
memo1.Lines.Add('Ｃ 修正値 ＝ ' + floatTostr(Cd));
if loop > KP then begin
memo1.Lines.Add('カテナリー数収束せずループ数超えました。');
memo1.Lines.Add('線の長さが直線距離に近すぎるか長すぎます。');
timer1.Enabled := False;
Button1.Enabled := True;
Tf := False;;
end;
end;
// 長さからカテナリー数計算
procedure TForm1.Calced;
const
KP = 500000; // 最大ループ数
// KP = 100; // 最大ループ数
var
eps: double;
Cd : double;
Ls : double;
C2 : double;
Lm : double;
Loop : integer;
begin
eps := 2.0E-15 * L; // 判定値
C2 := 2; // カテナリー数初期値
Cd := 256; // カテナリー数補助値
Loop := 0; // ループ数 無限ループ対策
Ls := sqrt(L * L - h * h);
repeat
Lm := C2 * sinh(S / C2);
if Ls < Lm then C2 := C2 + Cd;
if Ls > Lm then begin
C2 := C2 - Cd;
Cd := Cd / 2;
C2 := C2 + Cd;
end;
inc(Loop); // ループ数インクリメント
until (Cd < eps) or (Ls = Lm) or (Loop > KP);
C := C2 / 2;
memo1.Lines.Add('Loop数 ＝ ' + intTostr(Loop));
memo1.Lines.Add('Ｃ 修正値 ＝ ' + floatTostr(Cd));
if loop > KP then begin
memo1.Lines.Add('カテナリー数収束せずループ数超えました。');
memo1.Lines.Add('線の長さが直線距離に近すぎるか長すぎます。');
timer1.Enabled := False;
Button1.Enabled := True;
Tf := False;;
end;
end;
// --------- カテナリー数計算 ニュートン法 -----------------------
// 差分計算
function TForm1.f(Ct, S, sL2mh2: double): double;
begin
result := 2.0 * Ct * sinh(S / (Ct * 2.0)) - sL2mh2;
end;
// 微分
function TForm1.dfdx(Ct, S: double): double;
begin
result := 2.0 * sinh(S / (2.0 * Ct)) - (S * cosh(S / (2.0 * Ct)) / Ct);
end;
// カテナリー数近似値
function TForm1.f_inverse(S, Lh: double): double;
var
a0, b0, c0, d0, e0:double;
begin
a0 := S - Lh; // *注 Lh は符号が反対
b0 := power(S, 3) / 24;
c0 := power(S, 5) / 1920;
d0 := sqrt(b0 * b0 - 4 * a0 * c0);
e0 := (- b0 - d0) / 2 / a0;
result := sqrt(e0);
end;
// カテナリー数収束計算 ニュートン法
// 長さが長くなったら収束判定値大きくしないと桁落ちの為収束判定できなくなります。
function TForm1.f_inverse_newton(S, sL2mh2: double): double;
const
Kp = 1000;
var
Ct : double;
fvalue, fback: double;
move : double;
eps : double;
i, n : integer;
begin
eps := 1.0E-15 * L; // 判定値 長さで制御
Ct := f_inverse(S, sL2mh2); // 近似値
fvalue := f(Ct, S, sL2mh2); // 差分
n := 0;
for i := 0 to Kp do begin
fback := abs(fvalue); // 桁落ち収束チェック用
move := fvalue / dfdx(Ct, S); // 補正値
Ct := Ct - move; // 新カテナリー数
fvalue := f(Ct, S, sL2mh2); // 差分
inc(n);
if (abs(fvalue) < eps) or (fback = fvalue) then break;
end;
memo1.Lines.Add('Loop数 ＝ ' + intTostr(n));
memo1.Lines.Add('Ｃ 修正値 ＝ ' + floatTostr(abs(fvalue)));
if n > kp then begin
memo1.Lines.Add('カテナリー数収束せずループ数超えました。');
memo1.Lines.Add('線の長さが直線距離に近すぎるか長すぎます。');
timer1.Enabled := False;
Tf := False;
Button1.Enabled := True;
end;
if Ct < 0 then begin
memo1.Lines.Add('線の長さが直線距離に近すぎます。');
timer1.Enabled := False;
Tf := False;
Button1.Enabled := True;
end;
result := Ct;
end;
// カテナリー数Cの値解析
function TForm1.solve_C(S, h, L: double): double;
begin
result := f_inverse_newton(S, sqrt(L * L - h * h));
end;
//--------------------------------------------------------------
// 懸垂線等分割位置の表示
procedure TForm1.CalcXY;
var
Ls : double;
Sb : double;
xs, y : double;
n : integer;
begin
for n := 1 to B - 1 do begin
Ls := L / B * n; // 線の長さ
Sb := C * (arcSinh(Ls / C - sinh(m / C))) + m; // 仮の支持位置
xs := Sb - m; // 撓み計算位置
y := C * (cosh(xs / C) - 1) - dm; // 高さ 低い方の支持位置を基準として計算
Series5.AddXY(Sb, y); // 分割位置
end;
end;
// 懸垂線計算の実行
procedure TForm1.Button1Click(Sender: TObject);
var
s1 : double;
lmin, lmax : double;
bmin, bmax : double;
mg : double;
Lm : double;
begin
Timer1.Enabled := False;
if not datainput then exit;
memo1.Clear;
if RadioGroup1.ItemIndex = 0 then C := solve_C(S, h, L);
if RadioGroup1.ItemIndex = 1 then Calc;
if RadioGroup1.ItemIndex = 2 then Calced;
Lm := (L - sqrt(S * S + h * h)) / L;
if Lm <= 1E-11 then
memo1.Lines.Add('指定長さが直線距離に近すぎ計算誤差が大きくなります。');
memo1.Lines.Add('カテナリー数 Ｃ＝ ' + floatTostr(C));
if C < 0 then exit;
m := S / 2 - C * arcsinh(h / (2 * C * sinh(S / 2 / C)));
memo1.Lines.Add('最大たるみ位置 ｍ＝ ' + floatTostr(m));
s1 := abs(m * 2);
dm := C * (cosh(s1 / 2 / C) - 1);
memo1.Lines.Add('最大位置 弛度 dm＝ ' + floatTostr(dm));
x := m + C * arcsinh(h / S);
memo1.Lines.Add('斜弛度位置 ｘ＝' + floatTostr(x));
d := x / S * h + C * (cosh(m / C) - cosh(arcsinh(h / S)));
memo1.Lines.Add('斜弛度 ｄ＝' + floatTostr(d));
memo1.Lines.Add('直線距離 ＝' + floatTostr(sqrt(h * h + S * S)));
if h > 0 then begin
lmin := -d;
lmax := h;
end
else begin
lmin := -d + h;
lmax := 0;
end;
bmin := 0;
bmax := S;
// グラフ縦横スケール設定
if bmax > lmax - lmin then begin
mg := (bmax - (lmax - lmin)) / 2;
lmax := lmax + mg;
lmin := lmin - mg;
end
else begin
mg := ((lmax - lmin) - bmax) / 2;
bmin := bmin - mg;
bmax := bmax + mg;
end;
Series1.Clear;
Series2.Clear;
Series3.Clear;
Series4.Clear;
Series5.Clear;
if checkbox1.Checked then begin
Series2.AddXY(bmin, lmax);
Series2.AddXY(bmin, lmin);
Series2.AddXY(bmax, lmin);
end;
application.ProcessMessages;
// グラフ表示
Drawing; // 懸垂線グラフ
CalcXY; // 線長等分割点表示
application.ProcessMessages;
if tf then Timer1.Enabled := True;
end;
// テスト計算スタートストップ
procedure TForm1.Button2Click(Sender: TObject);
var
ch : integer;
begin
Timer1.Interval := 20;
if Tf then begin
Tf := False;
timer1.Enabled := False;
Button1.Enabled := True;
end
else begin
val(S_Edit.Text, S, ch);
if ch <> 0 then exit;
val(h_Edit.Text, h, ch);
if ch <> 0 then exit;
timer1.Enabled := True;
Tf := True;
No := round(sqrt(S * S + h * h) + 1); // テスト計算長さ
Length_Edit.Text := intTostr(No);
Button1.Enabled := False;
end;
end;
// テスト計算用間隔タイマー
procedure TForm1.Timer1Timer(Sender: TObject);
begin
Length_Edit.Text := intTostr(No);
Button1Click(nil);
inc(No); // テスト計算長さ
if No > 500 then No := round(sqrt(S * S + h * h) + 1);
end;
end.
catenary_length.zip