次数の高い方程式を精度よく解くのには、多倍長演算が必須ですが、最初から多倍長演算でプログラムを組むのは困難なので、最初にDoubleの精度で組み、動作の確認後、多倍長演算のプログラムに変換しています。次数は、２０迄ですが、プログラムを修正すれば簡単に増やすことが出来ます。
入力値によっては、収束しない場合がありその場合は、５００ループで終了するようになっています。
多倍長演算でも、次数が多い場合は、演算の桁数を簡単に超えてしまいます。
高次方程式の解法(DKA法)
αn*xn
+ αn-1*xn-1
+ αn-2*xn-2
+ ・・・ + α1*x +
α0 = 0
上記ｎ次方程式の解法を行います。
解法は、Durand-Kerner-Aberth(DKA)法を使用します。
DKA法については、インターネットで検索すれば出てきますので、参照して下さい。
解は、近似値計算なので、値の近い解がある場合は、分離して解を出すのは困難なようです。
プログラムは、インターネットで検索したものを参考に作りました。
計算には複素数を使用するのですが、 Delphi
に用意されている複素数の計算は、非常に計算速度が遅いので、方程式の解法部分は、新たに複素数を用意し、四則演算も別に用意して高速化をはかりました。
又、Delphi 標準の複素数は、小さい方の値が、1E-11以下になると0(ゼロ)に丸められてしまうので、誤差の値を小さく収束させるような計算には不向きです。
検算のルーチンは、標準の複素数ルーチンを使用しています。
次数の高い方程式を精度よく解くのには、多倍長演算が必須ですが、最初から多倍長演算でプログラムを組むのは困難なので、最初にDoubleの精度で組み、動作の確認後、多倍長演算のプログラムに変換しています。
次数は、２０迄ですが、プログラムを修正すれば簡単に増やすことが出来ます。
入力値によっては、収束しない場合がありその場合は、５００ループで終了するようになっています。
多倍長演算でも、次数が多い場合は、演算の桁数を簡単に超えてしまいます。
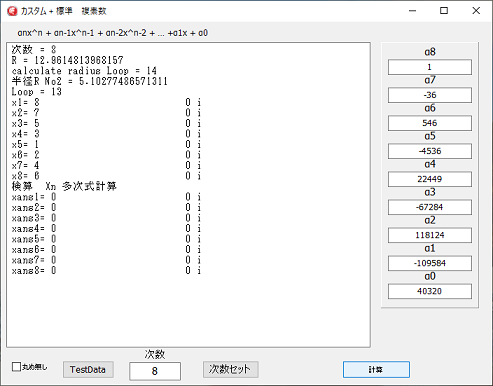
多倍長実行画面
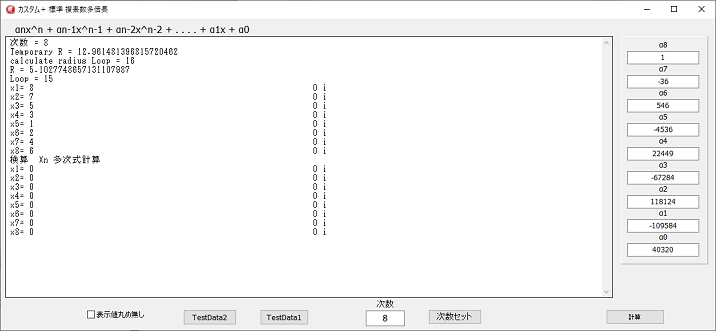次数の値をいれ、次数セットボタンをクリックすれば、設定した次数の値が入力できるようになります。
結果の値が正しいかどうかは、検算でゼロに成るかどうかで判定します。
計算誤差を見たい場合は、丸め無しにチェックを入れます。
プログラム 通常精度 Double
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, System.VarCmplx, system.Math,
Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Memo1: TMemo;
Button1: TButton;
Panel1: TPanel;
Label1: TLabel;
Button2: TButton;
LabeledEdit1: TLabeledEdit;
Button3: TButton;
CheckBox1: TCheckBox;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
var
NLabeledEdit: array of TLabeledEdit;
Nd : integer;
one : double = 1;
zero : double = 0;
type
TCdouble = record
r : double;
i : double;
end;
function MCdouble(r, i:double): TCdouble;
begin
result.r := r;
result.i := i;
end;
// a + b
function cadd(a, b: TCdouble): TCdouble;
begin
result.r := a.r + b.r;
result.i := a.i + b.i;
end;
// a - b
function csub(a, b: TCdouble): TCdouble;
begin
result.r := a.r - b.r;
result.i := a.i - b.i;
end;
// a * b
function cmul(a, b: TCdouble): TCdouble;
begin
result.r := a.r * b.r - a.i * b.i;
result.i := a.r * b.i + a.i * b.r;
end;
// a / b
function cdiv(a, b: TCdouble): TCdouble;
var
bb: double;
begin
result.r := 0;
result.i := 0;
bb := b.r * b.r + b.i * b.i;
if bb <> 0 then begin
result.r := (a.r * b.r + a.i * b.i) / bb;
result.i := (a.i * b.r - a.r * b.i) / bb;
end;
end;
function polynomial(p: array of double; x: double; n: integer): double;
var
i : integer;
r : double;
begin
r := p[n-1];
for i := n - 2 downto 0 do r := r * x + p[i];
result := r;
end;
// Durand Kerner Aberth algorithm
function dka(a: array of double; var c: array of TCdouble; n: integer): boolean;
var
r, r0, t : double;
e : double;
f, w, p, ca: TCdouble;
norm: double;
i, j, L: integer;
ba : array of double;
b : array of double;
db: array of double;
zc : double;
begin
setlength(ba, n + 1);
setlength(b, n + 1);
setlength(db, n);
// 半径の設定
for i := 0 to n do ba[i] := a[i];
zc := -ba[n-1] / n;
for i := 1 to n do
for j := n downto i do
ba[j-1] := ba[j-1] + ba[j] * zc;
for i := 0 to n - 1 do b[i] := -abs(ba[i]);
b[n] := ba[n];
r := 0; // 初期値
for i := 0 to n - 1 do begin
r0 := power(n * abs(b[i]), 1/(n-i));
if r < r0 then r := r0;
end;
Form1.Memo1.Lines.Add('R = ' + floatTostr(R));
for i := 1 to n do db[i-1] := b[i] * i; // db(r) = b'(r)
L := 0;
repeat // Newton's method
r0 := polynomial(b, r, n + 1) / polynomial(db, r, n);
r := r - r0;
inc(L);
until (abs(r0) < 1E-10) or (L > 100);
Form1.Memo1.Lines.Add('calculate radius Loop = ' + intTostr(L));
Form1.Memo1.Lines.Add('半径R No2 = ' + floatTostr(r));
for i := 1 to n do begin // 半径rの円に等間隔に配置する
t := 2 * PI / n * (i - 3 / 4.0);
c[i-1].r := r * cos(t) - a[n-1] / n; // アーバスの初期値
c[i-1].i := r * sin(t);
end;
L := 0;
repeat // 解法
e := 0; // 収束判別値
for i := 0 to n - 1 do begin
f := MCdouble(one, zero); // 分子 f(zi)
for j := n - 1 downto 0 do begin // ホーナー法
w := cmul(f, c[i]); // z
f.r := w.r + a[j]; // f=z+a[j]
f.i := w.i;
end;
p := MCdouble(one, zero);
for j := 0 to n - 1 do begin
if j <> i then begin
p := cmul(p, csub(c[i], c[j])); // p*(zi-zj)
end;
end;
t := p.r * p.r + p.i * p.i; // pの0値確認
if t = 0 then begin
application.MessageBox('分母がゼロです除算できません。', '注意', 0);
result := false;
exit;
end;
ca := cdiv(f, p);
norm := sqrt(ca.r * ca.r + ca.i * ca.i);
if e < norm then e := norm; // 最大値
c[i] := csub(c[i], ca); // L回目の近似根
end;
inc(L);
until (e < 1E-10) or (L > 500);
result := true;
Form1.Memo1.Lines.Add('Loop = ' + intTostr(L))
end;
// αnx^n + αn-1x^n-1 + αn-2x^n-2 + … +α1x + α0 の計算
function poly8(a: array of double; c : TCdouble; n: integer): TCdouble;
var
i : integer;
x : array of Variant;
fxn : array of Variant;
begin
setlength(x, n);
setlength(fxn, n + 1);
for i := 0 to n -1 do x[i] := varascomplex(x[i]); // VarComplexCreateはメモリーリークが
for i := 0 to n do fxn[i] := varascomplex(fxn[i]); // 発生します。
x[0].real := c.r;
x[0].imaginary := c.i;
for i := 1 to n - 1 do x[i] := x[0] * x[i - 1];
for i := n downto 1 do begin
fxn[i] .real := a[i];
fxn[i] .imaginary := zero;
fxn[i] := fxn[i] * x[i - 1];
end;
fxn[0].real := a[0];
fxn[0].imaginary := zero;
x[0] := fxn[0];
for i := 1 to n do x[0] := x[0] + fxn[i];
result.r := x[0].real;
result.i := x[0].imaginary;
end;
// 解法と結果表示
procedure TForm1.Button1Click(Sender: TObject);
var
a : array of double;
c : array of TCdouble;
s : TCdouble;
i, n, j, ch: integer;
fd : double;
ad : array of double;
li : int64;
scou : string;
begin
n := 0;
// ゼロでない値の場所の検索
for i := Nd downto 0 do begin
val(NLabeledEdit[i].Text, fd, ch);
if ch <> 0 then begin
scou := 'α' + intTostr(i - 1) + 'が数値ではありません。';
application.MessageBox(pchar(scou),'注意',0);
exit;
end;
if (fd <> 0) and (n = 0) then n := i; // ゼロでない位置 次数
end;
if n < 1 then begin
application.MessageBox('α1の値がゼロです、一次以下はありません。','注意',0);
exit;
end;
button1.Enabled := false;
// 次数で配列の確保
setlength(a, n + 1);
setlength(c, n);
// 全データーの配列の確保
setlength(ad, Nd + 1);
// データー入力処理
for i := n downto 0 do begin
val(NLabeledEdit[i].Text, a[i], ch);
end;
// 先頭の値を１に設定
for i := n - 1 downto 0 do begin
a[i] := a[i] / a[n];
end;
a[n] := 1;
memo1.Clear;
memo1.Lines.Add('次数 = ' + intTostr(n));
// dka法 計算
dka(a, c, n);
// 答え表示
for i := 0 to n-1 do begin
fd := c[i].r;
if not checkbox1.Checked then
if abs(fd) < 1E5 then begin
li := round(fd * 1E8); // 小数点8桁以下丸め
fd := li / 1E8;
end;
scou := 'x' + inttostr(i + 1) + '= ' + floatTostr(fd);
ch := length(scou);
ch := 30 - ch;
for j := 0 to ch do scou := scou + ' ';
fd := c[i].i;
if not checkbox1.Checked then
if abs(fd) < 1E5 then begin
li := round(fd * 1E8); // 小数点8桁以下丸め
fd := li / 1E8;
end;
memo1.Lines.Add(scou + floatTostr(fd) + ' i');
end;
// 検算
for i := 0 to Nd do begin // 入力値のコピー
ad[i] := 0;
if i <= n then ad[i] := a[i];
end;
memo1.Lines.Add('検算 Xn 多次式計算');
for j := 0 to n-1 do begin
s := poly8(ad, c[j], n); // n次式計算
fd := s.r;
if not checkbox1.Checked then
if abs(fd) < 1E5 then begin
li := round(fd * 1E7); // 小数点7桁以下丸め
fd := li / 1E7;
end;
scou := 'xans' + inttostr(j + 1) + '= ' + floatTostr(fd);
ch := length(scou);
ch := 30 - ch;
fd := s.i;
if not checkbox1.Checked then
if abs(fd) < 1E5 then begin
li := round(fd * 1E7); // 小数点7桁以下丸め
fd := li / 1E7;
end;
for i := 0 to ch do scou := scou + ' ';
memo1.Lines.Add(scou + floatTostr(fd) + ' i');
end;
button1.Enabled := true;
end;
// 次数セット
procedure TForm1.Button2Click(Sender: TObject);
var
i: integer;
testdata : double;
Total : double;
begin
if Nd <> 0 then begin
for i := 0 to nd do NLabeledEdit[i].Free;
Nd := 0;
end;
val(LabeledEdit1.Text, Nd, i);
if i <> 0 then begin
application.MessageBox('次数が間違っています。','注意',0);
Nd := 0;
exit;
end;
if Nd < 1 then begin
application.MessageBox('次数が少なすぎます。','注意',0);
Nd := 0;
exit;
end;
if Nd > 20 then begin
application.MessageBox('次数が多すぎます。','注意',0);
Nd := 0;
exit;
end;
height := 478 + (nd - 8) * 40 + 80;
panel1.Height := 380 + (Nd - 8) * 40;
LabeledEdit1.top := clientheight - 33;
button1.top := clientheight - 35;
button2.top := clientheight - 35;
button3.top := clientheight - 35;
memo1.Height := 356 + (Nd - 8) * 40 + 80;
checkbox1.top := clientheight - 35;
// top := (screen.Height - height) div 2;
// left := (screen.Width - width) div 2;
setlength(NLabeledEdit, Nd +1);
for i:=0 to Nd do NLabeledEdit[i] := nil;
for i:=0 to Nd do begin
NLabeledEdit[i] := TLabeledEdit.Create(form1.Panel1);
NLabeledEdit[i].Parent := form1.Panel1;
NLabeledEdit[i].Left:= 10;
NLabeledEdit[i].top := form1.Panel1.Height - 40 * (i) - 35;
NLabeledEdit[i].Width := 120;
NLabeledEdit[i].Alignment := tacenter;
NLabeledEdit[i].EditLabel.Font.Size := 11;
NLabeledEdit[i].EditLabel.Caption := 'α' + intTostr(i);
NLabeledEdit[i].Font.Size := 9;
NLabeledEdit[i].Text := floatTostr(power(10, i));
NLabeledEdit[i].Height := 22;
end;
total := 0;
for i:=1 to Nd do begin
testdata := 1;
total := total - testdata;
NLabeledEdit[i].Text := floatTostr(testdata);
end;
NLabeledEdit[0].Text := floatTostr(total);
button1.Enabled := true;
end;
// テストデーターセット
procedure TForm1.Button3Click(Sender: TObject);
begin
LabeledEdit1.Text := '8';
button2Click(nil);
NLabeledEdit[0].Text := '40320';
NLabeledEdit[1].Text := '-109584';
NLabeledEdit[2].Text := '118124';
NLabeledEdit[3].Text := '-67284';
NLabeledEdit[4].Text := '22449';
NLabeledEdit[5].Text := '-4536';
NLabeledEdit[6].Text := '546';
NLabeledEdit[7].Text := '-36';
NLabeledEdit[8].Text := '1';
end;
// 初期画面設定
procedure TForm1.FormCreate(Sender: TObject);
begin
width := 718;
height := 478 + 80;
top := (screen.Height - height) div 2;
left := (screen.Width - width) div 2;
button1.Enabled := False;
panel1.Width := 140;
panel1.Height := 380;
panel1.top := 29;
panel1.Left := 543;
memo1.Left := 8;
memo1.Height := 356 + 80;
memo1.Width := 520;
memo1.Top := 29;
LabeledEdit1.Top := clientheight - 33;
button1.top := clientheight - 35;
button2.top := clientheight - 35;
button3.top := clientheight - 35;
checkbox1.top := clientheight - 35;
Nd := 0;
end;
end.
多倍長演算プログラム
多倍長の組み込みは
MPArithからmparith_2018-11-27.zipをダウンロードします。
ファイルの日付が変わるので、変わっていたら新しいのをダウンロードして下さい。
Zipファイルを解凍して、解凍したフォルダーにパス(ツール->オプション->Delphiオプション->ライブラリ->ライブラリパス)を追加し、Uses に mp_types, mp_real, mp_cmplx, mp_baseを追加すれば使用可能になります。
一般の四則演算(=+-*/)は使用できず全て専用のルーチンとなるのでプログラムが長くなります。
使用方法は、ホームページ及び、ｈeｌｐファイルを見れば分かりますが、ｈeｌｐファイルは古いタイプなので、Win10で見るためには、変換をするか、WinHlp32.exeを入れ替える必要があります。
複素数演算も充実していますが、複素数の演算速度は非常に遅いので、四則演算は Double の時と同じように専用のルーチンを用意しました。
特に指定した値に収束できないとき、最大Loop数に達するのに非常に時間が掛かるのを避ける為です。
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, system.Math, Vcl.ExtCtrls, mp_types, mp_real,
mp_cmplx, mp_base;
type
TForm1 = class(TForm)
Memo1: TMemo;
Button1: TButton;
Panel1: TPanel;
Label1: TLabel;
LabeledEdit1: TLabeledEdit;
Button2: TButton;
Button3: TButton;
Button4: TButton;
CheckBox1: TCheckBox;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
procedure Button4Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
var
// LabeledEdit配列
NLabeledEdit: array of TLabeledEdit;
Nd : integer;
// Cmp.re = r cmp.im = i
procedure Cmpset(var Cmp: mp_complex; r, i: mp_float);
begin
mpf_copy(r, Cmp.re);
mpf_copy(i, Cmp.im);
end;
// cmp = a + b
procedure mcadd(a, b: mp_complex; var cmp: mp_complex);
begin
mpf_add(a.re, b.re, cmp.re);
mpf_add(a.im, b.im, cmp.im);
end;
// cmp = a - b
procedure mcsub(a, b: mp_complex; var cmp: mp_complex);
begin
mpf_sub(a.re, b.re, cmp.re);
mpf_sub(a.im, b.im, cmp.im);
end;
// cmp = a * b
procedure mcmul(a, b: mp_complex; var cmp: mp_complex);
var
arebre, aimbim : mp_float;
arebim, aimbre : mp_float;
begin
mpf_init2(arebre, aimbim);
mpf_init2(arebim, aimbre);
mpf_mul(a.re, b.re, arebre);
mpf_mul(a.im, b.im, aimbim);
mpf_mul(a.re, b.im, arebim);
mpf_mul(a.im, b.re, aimbre);
mpf_sub(arebre, aimbim, cmp.re);
mpf_add(arebim, aimbre, cmp.im);
mpf_clear2(arebre, aimbim);
mpf_clear2(arebim, aimbre);
end;
// cmp = a / b
procedure mcdiv(a, b: mp_complex; var cmp: mp_complex);
var
bb, tmp0, tmp1: mp_float;
begin
mpf_init3(bb, tmp0, tmp1);
mpf_set0(cmp.re);
mpf_set0(cmp.im);
mpf_mul(b.re, b.re, tmp0);
mpf_mul(b.im, b.im, tmp1);
mpf_add(tmp0, tmp1, bb);
if not mpf_is0(bb) then begin
mpf_mul(a.re, b.re, tmp0);
mpf_mul(a.im, b.im, tmp1);
mpf_add(tmp0, tmp1, tmp0);
mpf_div(tmp0, bb, cmp.re);
mpf_mul(a.im, b.re, tmp0);
mpf_mul(a.re, b.im, tmp1);
mpf_sub(tmp0, tmp1, tmp0);
mpf_div(tmp0, bb, cmp.im);
end;
mpf_clear3(bb, tmp0, tmp1);
end;
// leng = a.re * a,re + a.im * a.im
procedure mcleng(a: mp_complex; var leng: mp_float);
var
tmpa, tmpb: mp_float;
begin
mpf_init2(tmpa, tmpb);
mpf_mul(a.re, a.re, tmpa);
mpf_mul(a.im, a.im, tmpb);
mpf_add(tmpa, tmpb, leng);
mpf_clear2(tmpa, tmpb);
end;
procedure polynomial(p: array of mp_float; x: mp_float; n: integer; var ans: mp_float);
var
i : integer;
r : mp_float;
begin
mpf_init(r);
mpf_copy(p[n - 1], r);
for i := n - 2 downto 0 do begin
mpf_mul(r, x, r);
mpf_add(r, p[i], r); // r := r * x + p[i];
end;
mpf_copy(r, ans);
mpf_clear(r);
end;
// Durand Kerner Aberth algorithm
function dka(a : array of mp_float; var c: array of mp_complex; n: integer): boolean;
label
EXT;
var
r, r0, t : mp_float;
e, norm : mp_float;
f : mp_complex;
p, ca : mp_complex;
ctmp : mp_complex;
one, zero, tmp, tmp1 : mp_float;
mpi, mp3s4, pi2, anm1 : mp_float;
EM60 : mp_float;
eback : mp_float;
i, j, L: integer;
b : array of mp_float;
ba : array of mp_float;
db : array of mp_float;
zc : mp_float;
begin
mpf_init3(r, r0, t);
mpf_init2(e, norm);
mpc_init(f);
mpc_init2(p, ca);
mpc_init(ctmp);
mpf_init4(one, zero, tmp, tmp1);
mpf_init4(mpi, mp3s4, pi2, anm1);
mpf_init(EM60);
mpf_init(eback);
mpf_init(zc);
setlength(b, n + 1);
setlength(ba, n + 1);
setlength(db, n);
for i := 0 to n do mpf_init(b[i]);
for i := 0 to n do mpf_init(ba[i]);
for i := 0 to n - 1 do mpf_init(db[i]);
// 定数セット-----------------
mpf_set1(one); // 1
mpf_set0(zero); // 0
mpf_set_pi(mpi); // pi π
mpf_exp10i(60, EM60);
mpf_inv(EM60, EM60); // 1E-60
mpf_set_int(tmp1, 3); // tmp1 = 3
mpf_div_int(tmp1, 4, mp3s4); // mp3s4 = 3/4
mpf_mul_int(mpi, 2, tmp1); // pi * 2
mpf_div_int(tmp1, n, pi2); // pi2 = 2 * pi / n
mpf_div_int(a[n-1], n, anm1); // anm1 = a[n-1] / n
mpf_chs(anm1, zc); // zc = -a[n-1] / n
// 半径の設定------------------
for i := 0 to n do mpf_copy(a[i], ba[i]); // ba[] = a[]
for i := 1 to n do
for j := n downto i do begin
mpf_mul(ba[j], zc, tmp1); // ba[j] * zc
mpf_add(ba[j-1], tmp1, ba[j-1]); // ba[j-1] := ba[j-1] + ba[j] * zc
end;
for i := 0 to n - 1 do begin // b[] = -abs(ba[]);
mpf_abs(ba[i], b[i]);
mpf_chs(b[i], b[i]);
end;
mpf_copy(ba[n], b[n]); // b[n] = ba[n]
mpf_set0(r); // 半径rの初期値 0
for i := 0 to n - 1 do begin // 半径rの仮値設定
j := n - i;
mpf_div_int(one, j, tmp1); // 1/(n-i)
mpf_abs(b[i], tmp);
mpf_mul_int(tmp, n, tmp); // absb[i] * n
if s_mpf_is_gt0(tmp) then begin
mpf_expt(tmp, tmp1, r0); // poewr(n * b[i], 1/(n-j))
end
else mpf_set0(r0); // r0 = 0
if mpf_is_lt(r, r0) then mpf_copy(r0, r); // r < r0 r = r0
end;
Form1.Memo1.Lines.Add('Temporary R = ' + string(mpf_decimal_alt(r, 20)));
for i := 1 to n do mpf_mul_int(b[i], i, db[i - 1]); // db(r) = b'(r)
L := 0; // ループカウンター
repeat // Newton's method 半径の設定
polynomial(b, r, n + 1, tmp);
polynomial(db, r, n, tmp1);
mpf_div(tmp, tmp1, r0);
mpf_sub(r, r0, r);
inc(L);
until mpf_is_lt(r0, EM60) or (L > 500);
Form1.Memo1.Lines.Add('calculate radius Loop = ' + intTostr(L));
Form1.Memo1.Lines.Add('R = ' + string(mpf_decimal_alt(r, 20)));
// 半径rの円に等間隔に配置----- r
for i := 1 to n do begin
mpf_set_int(tmp, i); // i
mpf_sub(tmp, mp3s4, tmp); // i - 3/4
// アーバスの初期値
mpf_mul(pi2, tmp, t); // t = 2 * pi / n * (i - 3/4)
mpf_cos(t, tmp); // cos(t)
mpf_mul(tmp, r, tmp); // r * cos(t)
mpf_sub(tmp, anm1, c[i-1].re); // c[i-1].re = r * cos(t) - a[n-1] / n
mpf_sin(t, tmp); // sin(t);
mpf_mul(r, tmp, c[i-1].im); // c[i-1].im = r * sin(t);
end;
// 解法----------------------------
L := 0; // ループカウンター
mpf_set0(e); // e = 0;
repeat
mpf_copy(e, eback); // eback = e
mpf_set0(e); // e = 0;
for i := 0 to n -1 do begin
mpc_set_mpf(f, one, zero); // f = (1, 0i)
for j := n - 1 downto 0 do begin // ホーナー法
mcmul(f, c[i], ctmp); // f * c[i]
mpf_add(ctmp.re, a[j], f.re); // f = f * c[i] + a[j]
mpf_copy(ctmp.im, f.im);
end;
Cmpset(p, one, zero); // p = (1, 0i)
for j := 0 to n - 1 do begin
if j <> i then begin
mcsub(c[i], c[j], ctmp); // c[i] - c[j]
mcmul(p, ctmp, p); // p = p * (c[i] - c[j])
end;
end;
mcleng(p, t); // t = p.re * p,re + p.im * p.im
if s_mpf_is0(t) then begin
application.MessageBox('分母がゼロで除算出来ません。', '注意', 0);
result := false;
goto EXT;
end;
mcdiv(f, p, ca); // ca = f / p
mcleng(ca, tmp); // ca.re * ca,re + ca.im * ca.im
mpf_sqrt(tmp, norm); // norm = √(ca,re * ca.re + ca.im * ca.im)
if mpf_is_lt(e, norm) then mpf_copy(norm, e); // 最大値
mcsub(c[i], ca, c[i]); // c[i] = c[i] - ca
end;
inc(L);
until mpf_is_lt(e, EM60) or mpf_is_eq(e, eback) or (L > 1000); // 収束しなかったら限度回数で終了
//---------------------------------
result := true;
Form1.Memo1.Lines.Add('Loop = ' + intTostr(L));
EXT:
mpf_clear3(r, r0, t);
mpf_clear2(e, norm);
mpc_clear(f);
mpc_clear2(p, ca);
mpc_clear(ctmp);
mpf_clear4(one, zero, tmp, tmp1);
mpf_clear4(mpi, mp3s4, pi2, anm1);
mpf_clear(EM60);
mpf_clear(eback);
mpf_clear(zc);
for i := 0 to n do mpf_clear(b[i]);
for i := 0 to n do mpf_clear(ba[i]);
for i := 0 to n - 1 do mpf_clear(db[i]);
end;
// αnx^n + αn-1x^n-1 + αn-2x^n-2 + ...............+ α1x + α0 の計算
// MPArithの複素数計算
procedure poly8(a: array of mp_float; c:mp_complex; n: integer ;var ans: mp_complex);
var
i : integer;
mzero : mp_float;
tmp : mp_complex;
x : array of mp_complex;
fxn : array of mp_complex;
begin
setlength(x, n);
setlength(fxn, n + 1);
mpf_init(mzero);
mpc_init(tmp);
for i := 0 to n -1 do mpc_init(x[i]);
for i := 0 to n do mpc_init(fxn[i]);
mpf_set0(mzero);
mpf_copy(c.re, x[0].re); // x[0] = x
mpf_copy(c.im, x[0].im);
for i := 1 to n - 1 do mpc_mul(x[0], x[i - 1], x[i]); // x[i] = x^(n+1)
for i := n downto 1 do begin
mpc_set_mpf(tmp, a[i], mzero); // (a[i], 0)
mpc_mul(tmp, x[i - 1], fxn[i]); // fxn[i] = a[i] * x^i
end;
mpc_set_mpf(fxn[0], a[0], mzero); // fxn[0] = (a[0], 0i)
mpc_copy(fxn[0], ans); // ans = fxn[0];
for i := 1 to n do // ans = ans + fxn[i]
mpc_add(ans, fxn[i], ans);
mpf_clear(mzero);
mpc_clear(tmp);
for i := 0 to n -1 do mpc_clear(x[i]);
for i := 0 to n do mpc_clear(fxn[i]);
end;
// 方程式の解法と結果表示
procedure TForm1.Button1Click(Sender: TObject);
var
a : array of mp_float;
c : array of mp_complex;
ad : array of mp_float;
md : mp_float;
tmp : mp_float;
s : mp_complex;
i, n, j, ch : integer;
fd : double;
scou : string;
xr, xi : array of mp_float;
ar, ai : array of mp_float;
lg, lt : mp_float;
intx : mp_int;
// 小数点50桁以下丸め 整数部が10桁以上の場合丸め無し
procedure roundX(var xir, xx, lg, lc: mp_float; var ii: mp_int);
begin
mpf_abs(xir, xx);
if mpf_is_gt(xx, lc) or checkBox1.Checked then begin
mpf_copy(xir, xx);
exit;
end;
mpf_mul(xir, lg, xx);
mpf_round(xx, ii);
mpf_set_mpi(xx, ii);
mpf_div(xx, lg, xx);
end;
begin
n := 0;
// ゼロでない値の場所の検索
for i := Nd downto 0 do begin
val(NLabeledEdit[i].Text, fd, ch);
if ch <> 0 then begin
scou := 'α' + intTostr(i) + 'が数値ではありません。';
application.MessageBox(pchar(scou),'注意',0);
exit;
end;
if (fd <> 0) and (n = 0) then n := i; // ゼロでない位置 次数
end;
if n < 1 then begin
application.MessageBox('α1の値がゼロです、一次以下はありません。','注意',0);
exit;
end;
button1.Enabled := False;
// 次数で配列の確保
setlength(a, n + 1); // 入力データー
setlength(c, n); // 計算用
setlength(xr, n); // 結果丸め表示用
setlength(xi, n); // 結果丸め表示用
setlength(ar, n); // 検算用
setlength(ai, n); // 検算用
// 全データーの配列の確保
setlength(ad, Nd + 1);
// 多倍長変数初期化
for i := 0 to n do mpf_init(a[i]);
for i := 0 to n - 1 do mpc_init(c[i]);
for i := 0 to Nd do mpf_init(ad[i]);
for i := 0 to n - 1 do mpf_init2(xr[i], xi[i]);
for i := 0 to n - 1 do mpf_init2(ar[i], ai[i]);
mpf_init2(lg, lt);
mp_init(intx);
mpf_init2(md, tmp);
mpc_init(s);
// データー入力処理 ゼロを除く先頭から
for i := n downto 0 do begin
mpf_read_decimal(a[i], pansichar(ansistring(NLabeledEdit[i].Text)));
end;
memo1.Clear;
memo1.Lines.Add('次数 = ' + intTostr(n));
for i := 0 to Nd do begin // 入力値のコピー 検算用
mpf_set0(ad[i]);
if i <= n then mpf_copy(a[i], ad[i]);
end;
// 先頭の値を１に設定
for i := n-1 downto 0 do begin
mpf_div(a[i], a[n], a[i]);
end;
mpf_set1(a[n]);
// dka法 計算
dka(a, c, n);
// 答え表示
mpf_exp10i(10, lt); // 1E10
mpf_exp10i(50, lg); // 1E50
// 表示用丸め
for i := 0 to n-1 do begin
roundX(c[i].re, xr[i], lg, lt, intx);
roundX(c[i].im, xi[i], lg, lt, intx);
poly8(ad, c[i], n, s); // 検算 n次式計算
roundX(s.re, ar[i], lg, lt, intx);
roundX(s.im, ai[i], lg, lt, intx);
end;
// 計算結果 表示
for i := 0 to n-1 do begin
if not checkBox1.Checked then begin
scou := 'x' + inttostr(i + 1) + '= ' + string(mpf_decimal_alt(xr[i], 50));
ch := length(scou);
ch := 62 - ch;
for j := 0 to ch do scou := scou + ' ';
memo1.Lines.Add(scou + string(mpf_decimal_alt(xi[i], 50)) + ' i');
end
else
begin
scou := 'x' + inttostr(i + 1) + '= ' + string(mpf_decimal_alt(xr[i], 80));
memo1.Lines.Add(scou);
scou := '';
for j := 0 to 62 do scou := scou + ' ';
memo1.Lines.Add(scou + string(mpf_decimal_alt(xi[i], 50)) + ' i');
end;
end;
// 検算 表示
memo1.Lines.Add('検算 Xn 多次式計算');
for j := 0 to n-1 do begin
scou := 'x' + inttostr(j + 1) + '= ' + string(mpf_decimal_alt(ar[j], 50));
ch := length(scou);
ch := 62 - ch;
for i := 0 to ch do scou := scou + ' ';
memo1.Lines.Add(scou + string(mpf_decimal_alt(ai[j], 50)) + ' i');
end;
// 多倍長変数の解放
for i := 0 to n do mpf_clear(a[i]);
for i := 0 to n - 1 do mpc_clear(c[i]);
for i := 0 to Nd do mpf_clear(ad[i]);
for i := 0 to n - 1 do mpf_clear2(xr[i], xi[i]);
for i := 0 to n - 1 do mpf_clear2(ar[i], ai[i]);
mpf_clear2(lg, lt);
mp_clear(intx);
mpf_clear2(md, tmp);
mpc_clear(s);
button1.Enabled := true;
end;
// 次数のセット
procedure TForm1.Button2Click(Sender: TObject);
var
i: integer;
testdata : double;
Total : double;
begin
if Nd <> 0 then begin
for i := 0 to Nd do NLabeledEdit[i].Free;
Nd := 0;
end;
val(LabeledEdit1.Text, Nd, i);
if i <> 0 then begin
application.MessageBox('次数が間違っています。','注意',0);
Nd := 0;
exit;
end;
if Nd < 1 then begin
application.MessageBox('次数が少なすぎます。','注意',0);
Nd := 0;
exit;
end;
if Nd > 20 then begin
application.MessageBox('次数が多すぎます。','注意',0);
Nd := 0;
exit;
end;
height := 478 + (Nd - 8) * 40 + 80;
panel1.Height := 380 + (Nd - 8) * 40;
LabeledEdit1.top := clientheight - 33;
button1.top := clientheight - 35;
button2.top := clientheight - 35;
button3.top := clientheight - 35;
button4.top := clientheight - 35;
memo1.Height := 356 + (Nd - 8) * 40 + 80;
checkBox1.Top := clientheight - 35;
// top := (screen.Height - height) div 2;
// left := (screen.Width - width) div 2;
setlength(NLabeledEdit, Nd +1);
for i:=0 to Nd do NLabeledEdit[i] := nil;
for i:=0 to Nd do begin
NLabeledEdit[i] := TLabeledEdit.Create(form1.Panel1);
NLabeledEdit[i].Parent := form1.Panel1;
NLabeledEdit[i].Left:= 10;
NLabeledEdit[i].top := form1.Panel1.Height - 40 * (i) - 35;
NLabeledEdit[i].Width := 120;
NLabeledEdit[i].Alignment := tacenter;
NLabeledEdit[i].EditLabel.Font.Size := 10;
NLabeledEdit[i].EditLabel.Caption := 'α' + intTostr(i);
NLabeledEdit[i].Font.Size := 9;
NLabeledEdit[i].Text := floatTostr(power(10, i));
NLabeledEdit[i].Height := 22;
end;
total := 0;
for i:=1 to Nd do begin
testdata := 1;
total := total - testdata;
NLabeledEdit[i].Text := floatTostr(testdata);
end;
NLabeledEdit[0].Text := floatTostr(total);
button1.Enabled := true;
end;
// テストデーターセット
procedure TForm1.Button3Click(Sender: TObject);
begin
LabeledEdit1.Text := '8';
button2Click(nil);
NLabeledEdit[0].Text := '40320';
NLabeledEdit[1].Text := '-109584';
NLabeledEdit[2].Text := '118124';
NLabeledEdit[3].Text := '-67284';
NLabeledEdit[4].Text := '22449';
NLabeledEdit[5].Text := '-4536';
NLabeledEdit[6].Text := '546';
NLabeledEdit[7].Text := '-36';
NLabeledEdit[8].Text := '1';
end;
procedure TForm1.Button4Click(Sender: TObject);
begin
LabeledEdit1.Text := '4';
button2Click(nil);
NLabeledEdit[0].Text := '-30';
NLabeledEdit[1].Text := '31';
NLabeledEdit[2].Text := '5';
NLabeledEdit[3].Text := '-7';
NLabeledEdit[4].Text := '1';
end;
// 初期設定
procedure TForm1.FormCreate(Sender: TObject);
begin
height := 558;
width := 1156 + 50;
top := (screen.Height - height) div 2;
left := (screen.Width - width) div 2;
panel1.Caption := '';
button1.Enabled := False;
panel1.Width := 145;
panel1.Height := 380;
panel1.top := 29;
panel1.Left := 983 + 50;
memo1.Left := 8;
memo1.Height := 436;
memo1.Width := 961 + 50;
memo1.Top := 29;
LabeledEdit1.Top := clientheight - 33;
button1.top := clientheight - 35;
button2.top := clientheight - 35;
button3.top := clientheight - 35;
button4.top := clientheight - 35;
checkBox1.Top := clientheight - 35;
Nd := 0;
end;
end.
Durand_Kerner_Aberth.zip