ガンマ関数Γ(z)に対し、対数微分で定義される関数。
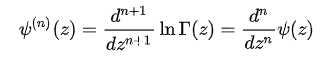
ウィキペディア ポリガンマ関数に詳しく説明があるのでそちらを参照してください。
ポリガンマ関数
ガンマ関数Γ(z)に対し、対数微分で定義される関数。
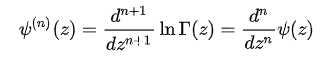
ウィキペディア ポリガンマ関数に詳しく説明があるのでそちらを参照してください。
値の計算は漸近展開によって計算されます。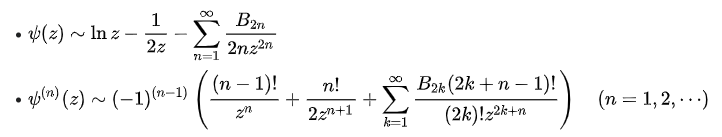
Ψ(z).Ψ(1)(z),Ψ(2)(z),Ψ(3)(z),Ψ(4)(z) ディ、トリ、テトラ、ペンタ、ヘキサ ガンマ関数とそれぞれ呼ばれていて、ディガンマ関数は本ホームページで既に取り上げていますが、ポリガンマ関数のプログラムは、計算式は違うが、ディガンマ関数を含めて計算するようになっています。
∑の計算は、無限大迄計算するようになっていますが、実際には不可能なので、必要な桁数に応じて、ベルヌーイ数をどこまで計算するかを決めます。
Zの値が、大きい場合は、誤差が小さくなりますが、値が小さい場合、誤差が大きくなるので、値を修正して計算結果が正しい値に近づくようにいます。
最初のプログラムは、応用統計学のポリ・ガンマ関数のC言語,およびFortran 77言語による算譜にあるC言語のものを、Delphi用に変換したものです。(ポリ・ガンマ関数のC言語,およびFortran 77言語による算譜の方がプログラムリストそのものをダウンロードできます。)
元のプログラムは、マイナス側の値を計算するようになっていませんでしたが、テストをした結果、問題なく計算できるようなので、計算出来る様に修正しました。
プログラムについては、応用統計学のポリ・ガンマ関数のC言語,およびFortran 77言語による算譜 からPDFファイルをダウンロードして読んでもらえばよく分かると思います。
プログラムリストはポリ・ガンマ関数のC言語,およびFortran 77言語による算譜からC言語のリストをダウンロードして、RAD Studio のコンソールアプリケーションとして、コンパイル、コマンドラインから実行すれば、少しの修正で、実行確認が出来ます。
Delphiに変換するに際して、多倍長演算の為にベルヌーイ数の数が自由に出来る様にしたり、不要な符号の設定の削除とかの修正をしました。
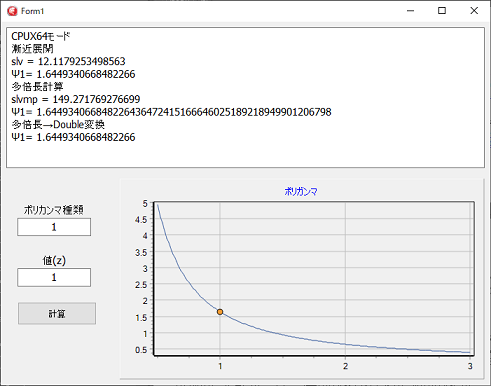左図は、X64のモードで、コンパイルし実行した場合です。
X64のモードなので、多倍長演算以外は全て、Doubleの精度で計算されています。
ポリガンマの種別は、0を含み０以上です。
-1は、対数ガンマを表しているので、必要であれば、ガンマ関数のプログラムで対数指定して計算してください。
プログラム
多倍長演算は、255桁まで計算可能ですが、精度60桁指定で計算し、50桁程表示しています。
多倍長の組み込みは MPArithからmparith_2018-11-27.zipをダウンロードし、Zipファイルを解凍して、解凍したフォルダーにパス(ツール->オプション->Delphiオプション->ライブラリ->ライブラリパス)を追加し、Uses
に mp_types, mp_real, mp_cmplx, mp_baseを追加すれば使用可能になります。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, system.Math, Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons,
system.UITypes, VclTee.TeeGDIPlus, VCLTee.Series, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart,
mp_types, mp_real, mp_base;
type
TForm1 = class(TForm)
BitBtn1: TBitBtn;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
Memo1: TMemo;
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
procedure BitBtn1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
var slvamp : double;
//=========================================================================================
// procedure polygamma_mp(km: integer; x: mp_float; var ans: mp_float var INFF: integer);
//
// km integer polygamma種別 k = 0～
// x mp_float 値
// ans mp_float 答え
// ans の精度は50桁以上 mpfの計算桁数は255桁
// INF integer 演算フラグ
// 値が∞又は-∞になる場合、値の設定が出来ないのでフラグ使用
// INFF 0 通常 1 演算結果∞ -1 演算経過-∞ 2 ボリガンマ種別Km<0
//
//=========================================================================================
procedure polygamma_mp(km: integer; x: mp_float; var ans: mp_float; var INFF: integer);
label
POYEND;
const
BRNTRM = 29;
BRNARY = BRNTRM - 12; // 100桁以上の精度を指定する場合は 12の値を小さくします
// ベルヌーイ数 分子
numerator: array[0..BRNTRM] of string = (
'1',
'-1',
'1',
'-1',
'5',
'-691',
'7',
'-3617',
'43867',
'-174611',
'854513',
'-236364091',
'8553103',
'-23749461029',
'8615841276005',
'-7709321041217',
'2577687858367',
'-26315271553053477373',
'2929993913841559',
'-261082718496449122051',
'1520097643918070802691',
'-27833269579301024235023',
'596451111593912163277961',
'-5609403368997817686249127547',
'495057205241079648212477525',
'-801165718135489957347924991853',
'29149963634884862421418123812691',
'-2479392929313226753685415739663229',
'84483613348880041862046775994036021',
'-1215233140483755572040304994079820246041491'
);
// ベルヌーイ数 分母
denominator: array[0..BRNTRM] of string = (
'6',
'30',
'42',
'30',
'66',
'2730',
'6',
'510',
'798',
'330',
'138',
'2730',
'6',
'870',
'14322',
'510',
'6',
'1919190',
'6',
'13530',
'1806',
'690',
'282',
'46410',
'66',
'1590',
'798',
'870',
'354',
'56786730'
);
var
i, j: integer;
s, y, x2, pk, pxk : mp_float;
slv : mp_float;
f : mp_float;
n : mp_int;
i2 : mp_int;
isgn : mp_float;
brn: array[0..BRNARY] of mp_float;
tmp0, tmp1, tmp2: mp_float;
kf :mp_float;
tmpi, k : mp_int;
// 階乗 m!
procedure factor(m: mp_int; var ans : mp_float);
var
i : mp_int;
begin
// 多倍長初期化 ----
mp_init(i);
// -----------------
mpf_set1(ans); // ans = 1
mp_set_int(i, 2); // i = 2
// for i := 2 to m do
while mp_is_le(i, m) do begin
mpf_mul_mpi(ans, i, ans); // ans = ans * i
mp_inc(i); // inc(i)
end;
// 多倍長解放 ----
mp_clear(i);
end;
// slv 漸近展開に適用される値
procedure slvcalc(k : mp_int; var ans: mp_float);
const
n = BRNARY + 1;
var
a , b, c, f :mp_float;
nn, ntmp : mp_int;
begin
// 多倍長初期化 ------
mpf_init4(a, b, c, f);
mp_init2(nn, ntmp);
// -------------------
mp_set_int(nn, n); // nn = int(n)
// a := 2 * abs(brn[BRNTRM]) * (2 * n + k - 1)!;
mp_mul_int(nn, 2, nn); // nn = 2n
mp_add(nn, k, ntmp); // ntmp = 2n + k
mp_dec(ntmp); // ntmp = 2n + k - 1
factor(ntmp, f); // f = (2n + k - 1)!
mpf_abs(brn[BRNARY], a); // a = abs(brn[BRNTRM])
mpf_mul_int(a, 2, a); // a = abs(brn[BRNTRM]) * 2
mpf_mul(a, f, a); // a = 2 * abs(brn[BRNTRM]) * (2n + k - 1)!
// b := brn[0] * (2 * n)! * (k + 1)!;
factor(nn, f); // f = (2n)!
mp_copy(k, ntmp); // ntmp = k
mp_inc(ntmp); // ntmp = k + 1
factor(ntmp, c); // c = (k + 1)!
mpf_mul(f, c, b); // b = (2n)! * (k + 1)!
mpf_mul(b, brn[0], b); // b = brn[0] * (2n)! * (k + 1)!
// c := a / b * 1e60; // 計算精度60桁
mpf_div(a, b, c); // c = a / b
mpf_mul_dbl(c, 1e60, c); // c = c * 1e60 // 150桁以上を指定すると異状に時間が増えます
// result := power(c, 1 / (2 * n - 2)); // その時はベルヌーイ数を増やします
mpf_set_mpi(b, nn); // b = float(nn) BRNARY = BRNTRM - 12 <- マイナス値を小さく
mpf_sub_int(b, 2, b); // b = 2n - 2
mpf_inv(b, a); // a = 1/(2n - 2)
mpf_expt(c, a, ans); // ans = c^a power(c ,1 / (2 * n - 2))
// 多倍長解放 ----------
mpf_clear4(a, b, c, f);
mp_clear2(nn, ntmp);
// ---------------------
end;
begin
// 多倍長初期化 ------------------------
mpf_init5(s, y, x2, pk, pxk);
mpf_init(slv);
mpf_init(f);
mp_init(n);
mp_init(i2);
mpf_init(isgn);;
for i := 0 to BRNARY do mpf_init(brn[i]);
mpf_init3(tmp0, tmp1, tmp2);
mpf_init(kf);
mp_init2(tmpi, k);
// --------------------------------------
mp_set_int(k, km); // km -> k
slvamp := 0;
//-----------------------------------------------------------------
// 分母がゼロになった時の値セット
// 多倍長から倍精度に変換したときinfinityになる値をセットします。
// 多倍長の値に無限大INFが無い為の処理です。
// INFFフラグ +無限大の時 INFF = 1 -無限大の時 -1 K<0の時 2 正常 0
//-----------------------------------------------------------------
{$IFDEF CPUX86} // プラットフォーム32ビット
begin
mpf_set_ext(tmp1, MaxExtended); // mpf -> dbl 変換時 INFにします Huge値
end;
{$ENDIF CPUX86}
{$IFDEF CPUX64} // プラットフォーム64ビット
begin
mpf_set_dbl(tmp1, Maxdouble); // tmp1 Maxdouble
mpf_Mul_dbl(tmp1, Maxdouble, tmp1); // Maxdouble^2 mpf -> dbl 変換時 INFにします Huge値
end;
{$ENDIF CPUX64}
mpf_chs(tmp1, tmp2); // tmp2 -Maxdouble^2 or -Mxxextended
mp_set_int(tmpi, 0); // tmpi 0
INFF := 0; // 通常エラーフラグ 0
// if K < 0 then
if mp_is_lt(k, tmpi) then begin
mpf_set0(ans); // ans = 0
INFF := 2; // 入力エラー
// exit;
goto POYEND; // 終了
end;
// if x <= 0 then begin
if s_mpf_is_le0(x) then begin // xの値が 0 or マイナスの時
// n := round(x);
mpf_round(x , n); // x丸め->n
mpf_set_mpi(tmp0, n); // n -> tmp0
// if n := x then begin
if mpf_is_eq(x, tmp0) then begin // xが整数なら
INFF := 1; // +∞ フラグセット
// result := maxdouble;
mpf_copy(tmp1, ans); // Huge - > ans
// i := k mod 2
mp_mod_int(k, 2, i); // ポリガンマ種別 mod 2
if i = 0 then begin // 偶数なら
// i := n mod 2
mp_abs(n, n); // nが負数だとmodの計算が出来ない(xの値)
mp_mod_int(n, 2, i); // n mod 2 (abs(x) mod 2)
if i = 1 then begin // 奇数だったら
mpf_copy(tmp2, ans); // -Huge -> ans
INFF := -1; // -∞ フラグセット
end;
// exit;
end;
goto POYEND; // 終了
end;
end;
// ベルヌーイ数の誤差を小さくする為、分子と分母に分けて計算で設定しています。
for i := 0 to BRNARY do begin
mpf_read_decimal(tmp0, pansichar(ansistring(numerator[i]))); // 分子
mpf_read_decimal(tmp1, pansichar(ansistring(denominator[i]))); // 分母
mpf_div(tmp0, tmp1, brn[i]);
end;
// slv := slvcalc(k);
slvcalc(k, slv); // 漸近展開に適用される値計算
// slvamp := slv;
slvamp := mpf_todouble(slv); // slv値表示の為なので無くても可
// pk := 1;
mpf_set1(pk);
// if k mod 2 = 1 then isgn := 1 else isgn := -1;
mp_mod_int(k, 2, i); // i = k mod 2
mpf_set1(isgn); // isgn = 1
if i = 0 then mpf_chs(isgn, isgn);
// for i := 0 to k - 1 do pk := pk * (i + 1);
for i := 0 to km - 1 do mpf_mul_int(pk, i + 1, pk);
// if x >= slv then begin
if mpf_is_ge(x, slv) then begin
// s := 0;
mpf_set0(s);
// x2 := x * x;
mpf_mul(x, x, x2);
// if k = 0 then begin // digamma
mp_is0(tmpi); // tmpi = 0
if mp_is_eq(k, tmpi) then begin // digamma
for i := BRNARY downto 0 do begin
mp_set_int(tmpi, i + 1); // tmp1 = i + 1
// i2 := 2 * (i + 1);
mp_mul_int(tmpi, 2, i2); // tmpi = 2 * (i + 1)
// s := s + brn[i] / i2;
mpf_div_mpi(brn[i], i2, tmp0); // tmp0 = brn[i] / i2;
mpf_add(s, tmp0, s); // s = brn[i] / i2 + 2
// s := s / x2;
mpf_div(s, x2, s);
end;
// s := ln(x) - 1 / (2 * x) - s;
mpf_ln(x, tmp0); // tmp0 = ln(x)
mpf_mul_int(x, 2, tmp1); // tmp1 = 2 * x
mpf_inv(tmp1, tmp1); // tmp1 = 1/(2 * x);
mpf_sub(tmp0, tmp1, tmp2); // tmp2 =ln(x) - 1/(2*x)
mpf_sub(tmp2, s, s); // s := ln(x) - 1/(2*x) - s
end
else begin // trigamma, tetragamma.....
for i := BRNARY downto 0 do begin
// f := 1;
mpf_set1(f);
// i2 := 2 * (i + 1);
mp_set_int(tmpi, i); // tmpi = i
mp_inc(tmpi); // tmpi = i + 1
mp_mul_int(tmpi, 2, i2); // i2 = i * 2
// j := i2 + k - 1;
mp_add(i2, k, tmpi); // tmpi = i2 + k
mp_dec(tmpi); // tmpi = i2 + k - 1
// while j > i2 do begin // "tmpi = j"
while mp_is_gt(tmpi, i2) do begin
// f := f * j;
mpf_mul_mpi(f, tmpi, f); // f = f * j
// dec(j);
mp_dec(tmpi);
end;
// s := s + brn[i] * f * isgn;
mpf_mul(brn[i], f, tmp0); // tmp0 = brn[i] * f
mpf_mul(tmp0, isgn, tmp1); // tmp1 = brn[i] * f * isgn
mpf_add(s, tmp1, s); // s := s + brn[i] * f * isgn
// s := s / x2;
mpf_div(s, x2, s);
end;
// pxk := 1;
mpf_set1(pxk);
// for i := 0 to k - 1 do begin
for i := 0 to km - 1 do begin
// s := s / x;
mpf_div(s, x, s);
// pxk := pxk * x;
mpf_mul(pxk, x, pxk);
end;
// s := s + pk * 1 / (2 * pxk * x) * isgn;
mpf_mul(pxk, x, tmp0); // tmp0 = pxk * x
mpf_mul_int(tmp0, 2, tmp1); // tmp1 = 2 * pxk * x
mpf_inv(tmp1, tmp0); // tmp0 = 1 / (2 * pxk * x)
mpf_mul(tmp0, isgn, tmp2); // tmp2 = 1 / (2 * pxk * x) * isgn
mpf_mul(tmp2, pk, tmp0); // tmp0 = pk * 1 / (2 * pxk * x) * isgn
mpf_add(s, tmp0, s); // s + pk * 1 / (2 * pxk * x) * isgn
// f := pk / k;
mpf_div_mpi(pk, k, f);
// s := s + f / pxk * isgn;
mpf_div(f, pxk, tmp0); // tmp0 = f / pxk
mpf_mul(tmp0, isgn, tmp1); // tmp1 = f / pxk * isgn
mpf_add(s, tmp1, s); // s = s + f / pxk * isgn
end;
end
else begin // x < sly
// n := trunc(slv - x);
mpf_sub(slv, x, tmp0); // tmp0 = slv - x
mpf_trunc(tmp0, n); // n = trunc(slv - x)
// y := n + x + 1;
mp_add_int(n, 1, tmpi); // tmpi = n + 1
mpf_add_mpi(x, tmpi, y); // n + x + 1
polygamma_mp(km, y, s, INFF); // 再帰
// for i := 0 to n do begin
mp_set_int(tmpi, 0); // tmpi = 0 "i =0"
while mp_is_le(tmpi, n) do begin // while i <= n do begin
// y := y - 1;
mpf_sub_int(y, 1, y); // y - 1
mpf_abs(y, tmp0); // tmp0 = abs(y)
mpf_set_dbl(tmp1, 1e-3); // tmp1 = 1e-3
// if abs(y) < 1e-3 then begin
if mpf_is_lt(tmp0, tmp1) then begin
// if x > 0 then y := x - trunc(x + 0.5)
// else y := x - trunc(x - 0.5);
if s_mpf_is_gt0(x) then mpf_add_dbl(x, 0.5, tmp2) // tmp2 = x + 0.5
else mpf_sub_dbl(x, 0.5, tmp2); // tmp2 = x - 0.5
mpf_int(tmp2, tmp1); // tmp1 = trunc(tmp2)
mpf_sub(x, tmp1, y); // y = x - trunc(x+-0.5)
end;
// pxk := 1;
mpf_set_int(pxk , 1);
// for j := 0 to k - 1 do pxk := pxk * y;
for j := 0 to km - 1 do mpf_mul(pxk, y, pxk); // pxk := pxk * y
// s := s + isgn * pk / pxk / y;
mpf_mul(isgn, pk, tmp0); // tmp0 = isgn * pk
mpf_div(tmp0, pxk, tmp1); // tmp1 = isgn * pk / pxk
mpf_div(tmp1, y, tmp2); // tmp2 = isgn * pk / pxk / y
mpf_add(s, tmp2, s); // s = s + isgn * pk / pxk / y
mp_inc(tmpi); // inc(tmpi) "inc(i)"
end;
end;
// result = s;
mpf_copy(s, ans);
POYEND:
// 多倍長開放 ----------------------------
mpf_clear5(s, y, x2, pk, pxk);
mpf_clear(slv);
mpf_clear(f);
mp_clear(n);
mp_clear(i2);
mpf_clear(isgn);;
for i := 0 to BRNARY do mpf_clear(brn[i]);
mpf_clear3(tmp0, tmp1, tmp2);
mpf_clear(kf);
mp_clear2(tmpi, k);
//----------------------------------------
end;
//=========================================================================================
var
slva : double;
//============================================================================================
// function polygamma_brn(k: integer; x: double; var INFF: integer): double;
//
// https://www.jstage.jst.go.jp/article/jappstat1971/22/1/22_1_23/_article/-char/ja
// http://202.16.123.1/~tunenori/polygamma.html
//
// C のプログラムをdelphiに変換
// xの値がマイナスでも計算出来る様に変更
// 精度はポリガンマの精度はdouble計算で 14～15桁 extended(long double) で16～18桁程度です。
// x値が負数の時double 14～15桁 extended(long double)で16～18桁程度
// x64 Doubleモードの時 digamma のゼロ近辺の答えの有効桁は小数点以下14桁程度となります。
//
// X86モード時 extended X64モード時 Double
//
// K integer ポリガンマ種別 0～
// x extended 値
// 戻り値 extended
// INFF integer 演算フラグ 0 通常 -1 ∞ +1 +∞ +2 入力エラーK<0
// INFFはDouble,extendedでの計算には不要ですが、多倍長計算にあわせています
// モード０での結果ゼロ近辺の値 k = 0 x = 1.46163214496836235
//
//============================================================================================
function polygamma_brn(k: integer; x: extended; var INFF: integer): extended;
const
BRNTRM = 13;
BRNARY = BRNTRM - 4; // オリジナルのプログラムに合わせる為のものです。
// BRNARY = BRNTRM;
brn: array[0..BRNTRM] of extended = (1.0 / 6,
-1.0 / 30,
1.0 / 42,
-1.0 / 30,
5.0 / 66,
-691.0 / 2730,
7.0 / 6,
-3617.0 / 510,
43867.0 / 798,
-174611.0 / 330,
854513.0 / 138,
-236364091 / 2730,
8553103 / 6,
-23749461029 / 870
);
var
s, y, x2, pk, pxk : extended;
slv : extended; // 漸近展開に適用される十分に大きな値
f : extended;
n : integer;
i, j : integer;
i2, isgn : integer;
// 階乗 m!
function factor(m: integer): extended;
var
i : integer;
J : extended;
begin
j := 1;
for i := 2 to m do j := j * i;
result := j;
end;
// slv 漸近展開に適用される値
function slvcalc(k : integer): extended;
var
a , b, c :extended;
n : integer;
begin
n := BRNARY + 1;
a := 2 * abs(brn[BRNARY]) * factor(2 * n + k - 1);
b := brn[0] * factor(2 * n) * factor(k + 1);
{$IFDEF CPUX64} // プラットフォーム64ビット
begin
c := a / b * 1e16; // 計算精度16桁
end;
{$ENDIF CPUX64}
{$IFDEF CPUX86} // プラットフォーム32ビット
begin
c := a / b * 1e20; // 計算精度20桁
end;
{$ENDIF CPUX86}
result := power(c, 1 / (2 * n - 2));
end;
begin
INFF := 0; // 演算エラーフラグフラグ 0
slva := 0;
if k < 0 then begin
result := NAN; // result = 無効な値
INFF := 2; // 入力エラー
exit; // 終了
end;
if x <= 0 then begin // xの値が0 or マイナスの時
n := round(x);
if n = x then begin // xが整数の時
INFF := 1; // ∞ フラグセット
result := infinity; // 戻り値 ∞;
if k mod 2 = 0 then // ポリガンマが偶数の時
if n mod 2 <> 0 then begin // 奇数の-x値なら
result := -infinity; // 戻り値 -∞;
INFF := -1; // -∞ フラグセット
end;
exit; // 終了
end;
end;
slv := slvcalc(k);
slva := slv; // slv値表示の為なので無くても可
pk := 1;
if k mod 2 = 1 then isgn := 1 else isgn := -1;
for i := 0 to k - 1 do pk := pk * (i + 1);
if x >= slv then begin
s := 0;
x2 := x * x;
if k = 0 then begin // digamma
for i := BRNARY downto 0 do begin
i2 := 2 * (i + 1);
s := s + brn[i] / i2;
s := s / x2;
end;
s := ln(x) - 1 / (2 * x) - s;
end
else begin // trigamma, tetragamma.....
for i := BRNARY downto 0 do begin
f := 1;
i2 := 2 * (i + 1);
j := i2 + k - 1;
while j > i2 do begin
f := f * j;
dec(j);
end;
s := s + brn[i] * f * isgn;
s := s / x2;
end;
pxk := 1;
for i := 0 to k - 1 do begin
s := s / x;
pxk := pxk * x;
end;
s := s + pk * 1 / (2 * pxk * x) * isgn;
f := pk / k;
s := s + f / pxk * isgn;
end;
end
else begin // x < sly
n := trunc(slv - x);
y := n + x + 1;
s := polygamma_brn(k, y, INFF);
for i := 0 to n do begin
y := y - 1;
if abs(y) < 1e-3 then begin
if x > 0 then y := x - trunc(x + 0.5)
else y := x - trunc(x - 0.5);
end;
pxk := 1;
for j := 0 to k - 1 do pxk := pxk * y;
s := s + isgn * pk / pxk / y;
end;
end;
result := s;
end;
//=========================================================================================
procedure TForm1.BitBtn1Click(Sender: TObject);
var
sc : double;
n, ch : integer;
z, po : extended;
min, max, dx, zx: double;
dans : double;
x, ans: mp_float;
maxmp, absans : mp_float;
k : mp_int;
INFF : integer;
begin
val(LabeledEdit1.Text, n, Ch);
if ch <> 0 then begin
MessageDlg('種類に間違いがあります。', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
if n < 0 then begin
MessageDlg('負数のポリガンマ種別は計算出来ません', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
val(LabeledEdit2.Text, z, Ch);
if ch <> 0 then begin
MessageDlg('値zに間違いがあります。', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
if z > 1e100 then begin
MessageDlg('値zが大きすぎます。', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
if z < -1e10 then begin
MessageDlg('値zが小さすぎます。', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
bitbtn1.Enabled := False;
// 多倍長初期化------
mpf_init2(x, ans);
mp_init(k);
mpf_init2(maxmp, absans);
//-------------------
memo1.Clear;
Series1.Clear;
Series2.Clear;
{$IFDEF CPUX64} // プラットフォーム64ビット
begin // double 計算精度15桁
memo1.Lines.Add('CPUX64モード');
end;
{$ENDIF CPUX64}
{$IFDEF CPUX86} // プラットフォーム32ビット
begin // extended 計算精度19桁
memo1.Lines.Add('CPUX86モード');
end;
{$ENDIF CPUX86}
po := polygamma_brn(n, z, INFF);
memo1.Lines.Add('漸近展開');
memo1.Lines.Add('slv = ' + floatTostr(slva));
if INFF = 2 then memo1.Lines.Add('Ψ' + intTostr(n) + '入力エラー');
// if INFF = 1 then memo1.Lines.Add('Ψ' + intTostr(n) + '= ∞');
// if INFF = -1 then memo1.Lines.Add('Ψ' + intTostr(n) + '= -∞');
// if INFF = 0 then
memo1.Lines.Add('Ψ' + intTostr(n) + '= ' + floatTostrF(po, ffgeneral, 18, 3));
// グラフスケール設定とグラフ作図
sc := 1e3;
case n of
0 : sc := 1e3;
1 : sc := 1e4;
2 : sc := 1e5;
3 : sc := 1e8;
4 : sc := 1e10;
end;
if po > sc then po := sc;
if po < -sc then po := -sc;
Series2.AddXY(z, po);
min := z - 1;
if min <= 0 then
if z > 0 then min := z;
if min > 0 then
case n of
0 : min := 0.1;
1 : min := 0.2;
2 : min := 0.3;
3 : min := 0.4;
4 : min := 0.5;
end;
if abs(z) < min then min := z;
if z > 0.7 then min := Z - 0.5;
if z >= 3 then min := z - 2;
max := z + 2;
dx := (max - min) / 200;
for ch := 0 to 200 do begin
zx := min + ch * dx;
if zx <= 0 + dx then
if abs(zx - trunc(zx)) < dx / 2 then
if zx - trunc(zx) < 0 then zx := trunc(zx) - dx / 2
else zx := trunc(zx) + dx / 2;
po := polygamma_brn(n, zx, INFF);
if po > sc then po := sc;
if po < -sc then po := -sc;
Series1.AddXY(zx, po);
end;
// 多倍長text -> 数値
mp_read_decimal(k, pansichar(ansistring(Form1.LabeledEdit1.Text)));
mpf_read_decimal(x, pansichar(ansistring(Form1.LabeledEdit2.Text)));
// 多倍長ポリガンマ
polygamma_mp(n, x, ans, INFF);
memo1.Lines.Add('多倍長計算');
memo1.Lines.Add('slvmp = ' + floatTostr(slvamp));
if INFF = 2 then memo1.Lines.Add('Ψ' + intTostr(n) + 'ポリガンマ種別＜０');
if INFF = 1 then memo1.Lines.Add('Ψ' + intTostr(n) + '= ∞');
if INFF = -1 then memo1.Lines.Add('Ψ' + intTostr(n) + '= -∞');
if INFF = 0 then
memo1.Lines.Add('Ψ' + intTostr(n) + '= '+ string(mpf_decimal_alt(ans, 52)));
if INFF <> 2 then begin
dans := mpf_todouble(ans);
memo1.Lines.Add('多倍長→Double変換');
memo1.Lines.Append('Ψ' + intTostr(n) + '= '+ FloatTostrF(dans, ffgeneral, 18, 3));
end;
// 多倍長開放----
mpf_clear2(x, ans);
mp_clear(k);
mpf_clear2(maxmp, absans);
//---------------
bitbtn1.Enabled := True;
end;
end.
次のプログラムは、C言語辞典 アルゴリズム一覧からダウンロードした、c言語のポリガンマ関数をDelphiに変換したものです。
こちらのc言語のものは、RAD Studioその他のコンソールアプリケーションに読み込んで、コンパイルすれば、コマンドラインから修正せずに実行可能です。
プログラムは、ディガンマ関数と、トリ、テトラ、ペンタ、ヘキサ ガンマ関数の二つに完全に分かれています。
非常に簡単なプログラムになっていますが、精度は、上記の通常精度ものと殆ど変わりません。
元々のC言語のプログラムに近いルーチンと、ベルヌーイ数の数を変更できるルーチンのプログラムを作成しました。
ベルヌーイ数が変更できるルーチンの方は、一応extended有効桁数20桁にあわせてありますが、計算精度としては19桁程度になります。
ベルヌーイ数の数を増やした場合、同じ演算精度で良い場合は、補正値を小さくします。
mの値がベルヌーイ数の数となっていますが、この値を小さくして、演算精度にあわせます。
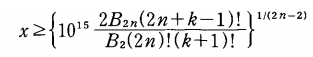
(k ポリガンマ種別)
上式は、前記のプログラムに使われている計算式で、15桁の精度でポリガンマの値を計算するものです。
これで計算して、その値をmの値に設定すれば、必要な精度の計算が出来るでしょう。
計算値に完全に合わせる必要はなく、多少大きめに設定しても問題はありません。
下記のプログラムは簡単なので、多倍長演算が出来るようにするのも簡単かと思います。
//----------------------------------------------------------------------- // http://chaste.web.fc2.com/Reference.files/Algo.html // Copyright (C) 2008-2015 Hidekazu Ito, Some rights reserved. // C のプログラムをdelphiに変換 //----------------------------------------------------------------------- unit main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, system.Math, Vcl.Buttons, Vcl.StdCtrls, Vcl.ExtCtrls, VclTee.TeeGDIPlus, VCLTee.Series, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart, system.UITypes; type TForm1 = class(TForm) Chart1: TChart; Series1: TLineSeries; Series2: TPointSeries; BitBtn1: TBitBtn; Memo1: TMemo; LabeledEdit2: TLabeledEdit; LabeledEdit1: TLabeledEdit; CheckBox1: TCheckBox; procedure BitBtn1Click(Sender: TObject); private { Private 宣言 } public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} const //ベルヌーイ数B(2)、B(4)、B(6)、...、B(20) B : array[1..10] of extended = ( 1.0 / 6, // B(2) -1.0 / 30, 1.0 / 42, -1.0 / 30, 5.0 / 66, -691.0 / 2730, 7.0 / 6, -3617.0 / 510, 43867.0 / 798, -174611.0 / 330); // B(20) m: integer = sizeof(B) div sizeof(extended); //--------------------------------------------------------------------- function psia(x: extended): extended; var k : integer; v, w, sum : extended; begin if x <= 0 then begin k := round(x); if k = x then begin if k mod 2 = 0 then result := infinity else result := -infinity; exit; end; end; v := 0; repeat v := v + 1 / x; x := x + 1; until x >= m; w := 1 / (x * x); sum := 0; for k := m downto 1 do begin sum := (sum + B[k] / (k * 2)) * w; end; v := v + sum + 0.5 / x; result := ln(x) - v; end; function polygammaa(n: integer; x: extended): extended; var k, k2 : integer; t, u, v, w : extended; begin if x <= 0 then begin k := round(x); if k = x then begin if n mod 2 = 0 then begin if k mod 2 = 0 then result := infinity else result := -infinity; end else result := infinity; exit; end; end; u := 1; for k := 1 - n to -1 do u := u * k; v := 0; repeat v := v + 1 / power(x, n + 1); x := x + 1; until x >= m ; w := x * x; t := 0; for k := m downto 1 do begin k2 := k * 2; t := (t + B[k]) * (n + k2 - 1) * (n + k2 - 2) / (k2 * (k2 - 1) * w); end; t := t + 0.5 * n / x + 1; result := u * (t / power(x, n) + n * v); end; //--------------------------------------------------------------------- //--------------------------------------------------------------------- function psi(x: extended): extended; var k : integer; v, w : extended; begin if x <= 0 then begin k := round(x); if k = x then begin if k mod 2 = 0 then result := infinity else result := -infinity; exit; end; end; v := 0; repeat v := v + 1 / x; x := x + 1; until x >= 8; w := 1 / (x * x); v := v + ((((((( (B[8] / 16) * w + (B[7] / 14)) * w + (B[6] / 12)) * w + (B[5] / 10)) * w + (B[4] / 8)) * w + (B[3] / 6)) * w + (B[2] / 4)) * w + (B[1] / 2)) * w + 0.5 / x; result := ln(x) - v; end; function polygamma(n: integer; x: extended): extended; var k : integer; t, u, v, w : extended; begin if x <= 0 then begin k := round(x); if k = x then begin if n mod 2 = 0 then begin if k mod 2 = 0 then result := infinity else result := -infinity; end else result := infinity; exit; end; end; u := 1; for k := 1 - n to -1 do u := u * k; v := 0; repeat v := v + 1 / power(x, n + 1); x := x + 1; until x >= 8; w := x * x; t := (((((((B[8] * (n + 15.0) * (n + 14) / (16 * 15 * w) + B[7]) * (n + 13.0) * (n + 12) / (14 * 13 * w) + B[6]) * (n + 11.0) * (n + 10) / (12 * 11 * w) + B[5]) * (n + 9.0) * (n + 8) / (10 * 9 * w) + B[4]) * (n + 7.0) * (n + 6) / ( 8 * 7 * w) + B[3]) * (n + 5.0) * (n + 4) / ( 6 * 5 * w) + B[2]) * (n + 3.0) * (n + 2) / ( 4 * 3 * w) + B[1]) * (n + 1.0) * n / ( 2 * w) + 0.5 * n / x + 1; result := u * (t / power(x, n) + n * v); end; //--------------------------------------------------------------------- procedure TForm1.BitBtn1Click(Sender: TObject); var n, ch : integer; x, po : extended; min, max, dx, zx, sc: extended; begin val(LabeledEdit1.Text, n, Ch); if ch <> 0 then begin MessageDlg('種類に間違いがあります。', mtInformation, [mbOk], 0, mbOk); exit; end; if n < 0 then begin MessageDlg('負数のポリガンマは計算出来ません', mtInformation, [mbOk], 0, mbOk); exit; end; val(LabeledEdit2.Text, x, Ch); if ch <> 0 then begin MessageDlg('値zに間違いがあります。', mtInformation, [mbOk], 0, mbOk); exit; end; bitbtn1.Enabled := False; memo1.Clear; Series1.Clear; Series2.Clear; {$IFDEF CPUX64} // プラットフォーム64ビット begin // double 計算精度15桁 memo1.Lines.Add('CPUX64モード'); end; {$ENDIF CPUX64} {$IFDEF CPUX86} // プラットフォーム32ビット begin // extended 計算精度19桁 memo1.Lines.Add('CPUX86モード'); end; {$ENDIF CPUX86} if n = 0 then begin if checkbox1.Checked = false then po := psi(x) else po := psia(x); end else begin if checkbox1.Checked = false then po := polygamma(n, x) else po := polygammaa(n, x); end; memo1.Lines.Add('Ψ' + intTostr(n) + '= ' + floatTostrF(po, ffgeneral, 18, 3)); // グラフスケール設定とグラフ作図 sc := 1e3; case n of 0 : sc := 1e3; 1 : sc := 1e4; 2 : sc := 1e5; 3 : sc := 1e8; 4 : sc := 1e10; end; if po > sc then po := sc; if po < -sc then po := -sc; Series2.AddXY(x, po); min := x - 1; if min <= 0 then if x > 0 then min := x; if min > 0 then case n of 0 : min := 0.1; 1 : min := 0.2; 2 : min := 0.3; 3 : min := 0.4; 4 : min := 0.5; end; if abs(x) < min then min := x; if x > 0.7 then min := x - 0.5; if x >= 3 then min := x - 2; max := x + 2; dx := (max - min) / 200; for ch := 0 to 200 do begin zx := min + ch * dx; if zx <= 0 + dx then if abs(zx - trunc(zx)) < dx / 2 then if zx - trunc(zx) < 0 then zx := trunc(zx) - dx / 2 else zx := trunc(zx) + dx / 2; if n = 0 then po := psi(zx) else po := polygamma(n, zx); if po > sc then po := sc; if po < -sc then po := -sc; Series1.AddXY(zx, po); end; bitbtn1.Enabled := True; end; end.
ploygamma_mp_function.zip