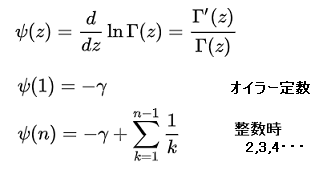
2020/07/02 171以上の値を入れた時の計算にミスが有ったので修正しました。
ディガンマ関数
ガンマ関数の対数微分で定義される特殊関数でポリガンマ関数の一種となっているようですが、詳細はインターネットで確認してください。
ディガンマ関数は、第２種ベッセル関数で使用されています。
第２種ベッセル関数では、整数のディガンマ関数しか使用されないので、簡単なプログラムで計算が可能なのですが、実数を扱えた方が便利なので、実数を扱えるディガンマ係数のCのプログラムをDelphi用に変換しました。
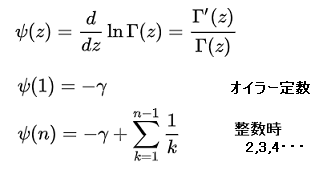
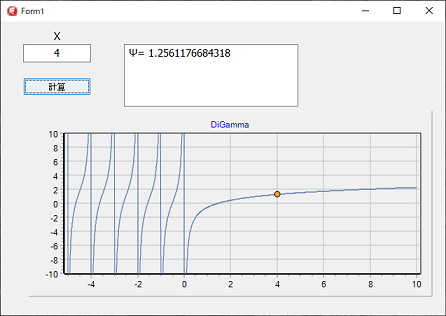Xの値実数のディガンマ関数を計算し、グラフ上にプロットします。
プログラム
//---------------------------------------------------------------------------- // DiGamma function // http://www.mymathlib.com/c_source/functions/gamma_beta/digamma_function.c // Mathematics Source Library C & ASM にあったものをDelphiに変換しました。 //---------------------------------------------------------------------------- unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls, system.UITypes, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) Memo1: TMemo; LabeledEdit1: TLabeledEdit; BitBtn1: TBitBtn; Chart1: TChart; Series1: TLineSeries; Series2: TPointSeries; procedure BitBtn1Click(Sender: TObject); private { Private 宣言 } public { Public 宣言 } function DiGamma_Function(x: double): double; function xDiGamma_Function(x: extended): extended; function xDiGamma(x: extended):extended; function xDiGamma_Asymptotic_Expansion(x: extended): extended; end; var Form1: TForm1; implementation {$R *.dfm} uses system.Math; /////////////////////////////////////////////////////////////////////////////// // ルーチン： // DiGamma_Function // xDiGamma_Function // // ディガ関数は、psi関数とも呼ばれ、xで評価されます // xで評価されたガンマ関数の対数の導関数です // つまり、psi（x）= d ln gamma（x）/ dx =（1 / gamma（x））d gamma（x）/ dx /////////////////////////////////////////////////////////////////////////////// const cutoff: double = 171.0; g: extended = 9.6565781537733158945718737389; a: array[0..8] of extended = ( +1.144005294538510956673085217e+4, -3.239880201523183350535979104e+4, +3.505145235055716665660834611e+4, -1.816413095412607026106469185e+4, +4.632329905366668184091382704e+3, -5.369767777033567805557478696e+2, +2.287544733951810076451548089e+1, -2.179257487388651155600822204e-1, +1.083148362725893688606893534e-4 ); //////////////////////////////////////////////////////////////////////////////// // double DiGamma_Function（double x） // // この関数はLanczosの式の対数の導関数を使用します // ガンマ関数がx> 1の場合DiGamma関数を計算、 // x <= cutoff = 171 DiGamma関数の漸近式 // x> cutoff の場合 The reflection formula // DiGamma（x）= DiGamma（1 + x）-1 / x // 0 <x <1.および reflection formulaの場合 // DiGamma（x）= DiGamma（1-x）-pi * cot（pi * x） // x <0の場合 // DiGamma関数は、正でない整数に特異点を持っています。 // 特異点では、MAXDoubleが返されます。 // //////////////////////////////////////////////////////////////////////////////// function TForm1.DiGamma_Function(x: double): double; var psi: extended; begin psi := xDiGamma_Function(x); if abs(psi) < MAXDouble then begin result := psi; exit; end; if psi < 0 then result := -MaxDouble else result := MaxDouble; end; //////////////////////////////////////////////////////////////////////////////// // //この関数はLanczosの式の対数の導関数を使用します //ガンマ関数がx> 1のDiGamma関数を計算し // x <=cutoff=171の場合DiGamma関数の漸近式 // x>cutoff の場合 The reflection formula // DiGamma（x）= DiGamma（1 + x）-1 / x // 0 <x <1.およびThe reflection formulaの場合 // DiGamma（x）= DiGamma（1-x）-pi * cot（pi * x） // x <0の場合 // DiGamma関数は、正でない整数に特異点を持っています。 // 特異点では、LDBL_MAXが返されます。 // psi = xDiGamma_Function（x）; // //////////////////////////////////////////////////////////////////////////////// function TForm1.xDiGamma_Function(x: extended): extended; var sin_x, cos_x: extended; ix: int64; begin if x > 0 then if x <= cutoff then begin if x >= 1 then result := xDiGamma(x) else result := xDiGamma(x + 1) - (1 / x); exit; end else begin result := xDiGamma_Asymptotic_Expansion(x); exit; end; // For a nonpositive argument (x <= 0). // If x is a singularity then return LDBL_MAX. if x > -MAXExtended then begin ix := trunc(x); if x = ix then begin result := MaxExtended; if ix mod 2 <> 0 then result := -result; exit; end; end; sin_x := sin(pi * x); if sin_x = 0 then begin result := MAXExtended; exit; end; cos_x := cos(pi * x); if abs(cos_x) = 1 then begin result := MAXExtended; exit; end; // If x is not a singularity then return DiGamma(x). result := xDiGamma(1 - x) - pi * cos_x / sin_x; end; //////////////////////////////////////////////////////////////////////////////// // // この関数はLanczosの式の対数の導関数を使用します// // ガンマ関数がx> 1のDiGamma関数を計算し、 // x <=cutoff=171 // g = xDiGamma（x） ////////////////////////////////////////////////// ////////////////////////////// function TForm1.xDiGamma(x: extended): extended; var lnarg, temp, term, numerator, denominator : extended; n, i: integer; begin lnarg := (g + x - 0.5); numerator := 0; denominator := 0; n := sizeof(a) div sizeof(extended); for i := n - 1 downto 0 do begin temp := x + i; term := a[i] / temp; denominator := denominator + term; numerator := numerator + term / temp; end; denominator := denominator + 1; result := ln(lnarg) - (g / lnarg) - numerator / denominator; end; //////////////////////////////////////////////////////////////////////////////// // xDiGamma_Asymptotic_Expansion（x: extended: extended; // // この関数は、漸近評価によりDiGamma（x）を推定します // DiGamma（x）〜ln（x）-（1/2）x + // B [2j] / [2j * x ^（2j）]の合計 // jは1から3で、B [2j]は2j番目のベルヌーイ数です。 // 精度的にはB[0]～B[2]でokですが、速度的には問題ないので // プログラムではB[0]～B[9]迄計算しています // g = xDiGamma_Asymptotic_Expansion（x） //////////////////////////////////////////////////////////////////////////////// // Bernoulli numbers B(2j) / 2j: B(2)/2,B(4)/4,B(6)/6,...,B(20)/20. Only // B(2)/2,..., B(6)/6 are currently used. const B: array[0..9] of extended = ( 1.0 / (6 * 2), -1.0 / (30 * 4), 1.0 / (42 * 6), -1.0 / (30 * 8), 5.0 / (66 * 10), -691.0 / (2730 * 12), 7.0 / (6 * 14), -3617.0 / (510 * 16), 43867.0 / (796 * 18), -174611.0 / (330 * 20) ); n : integer = sizeof(B) div sizeof(extended); function TForm1.xDiGamma_Asymptotic_Expansion(x: extended): extended; var m, i: integer; term: array of extended; sum, xx, xj, digamma : extended; begin m := n; // m := 3; // m = 3 で精度的にはOkです setlength(term, m); sum := 0; xx := x * x; xj := x; digamma := ln(xj) - 1 / (xj + xj); xj := xx; for i := 0 to m - 1 do begin term[i] := B[i] / xj; xj := xj * xx; end; for i := m - 1 downto 0 do sum := sum + term[i]; result := digamma - sum; end; // DiGamma関数の計算をします。 // グラフを描画 グラフ上にXの値をプロットします。 procedure TForm1.BitBtn1Click(Sender: TObject); var ch, i, n: integer; x, digamma : double; min, max, dx: double; begin val(labeledEdit1.Text, x, ch); if ch <> 0 then begin MessageDlg('X値に間違いがあります。', mtInformation, [mbOk], 0, mbOk); exit; end; // DiGamma計算 digamma := DiGamma_Function(x); memo1.Clear; memo1.Lines.Add('Ψ= ' + floattostr(digamma)); Series1.Clear; Series2.Clear; if digamma > 10 then digamma := 10; if digamma < -10 then digamma := -10; // グラフ上にプロット Series2.AddXY(x, digamma); min := -5; max := 10; n := 1000; dx := (max - min) / n; // グラフ描画 for i := 0 to n do begin x := dx * i + min; digamma := DiGamma_Function(x); if digamma > 15 then digamma := 15; if digamma < -15 then digamma := -15; Series1.AddXY(x, digamma); end; end; end.
Digamma_fanction.zip