2020/07/29
logGammaの計算をしてからexpでGammaの値を求めるプログラム例を追加しました。
2020/07/24
0< X <MINARG(5.5626846463e-309)でオバーフローするのを対策しました。
2020/07/16
１．一部DoubleとExtendedの設定ミスがあり修正しました。
２．入力値がマイナスの時の対数の値が出力できるようにしました、:計算結果は複素数として表示されます。
３．プラットフォームX64モードとX86モードの設定を追加しました。
(プラットフォームがX86の時は、Ln, power,sin,四則演算等は80ビットで計算されdoubleの精度64ビットに丸められますが、X64モードの時は、全て64ビットで演算されるため、同じDoubleの精度指定でも、X64モードの時は、精度が悪くな.る場合があります。)
ガンマ関数
周波数フーリエ変換で、カイザー窓関数を使用しましたが、その窓関数に、ベッセル関数が使用され、ベッセル関数にΓ関数が使用されていたので、Γ関数の計算です。
Γ関数を使用しなくても、ベッセル関数の値がが整数であれば、計算は可能です。
少し精度の高いGamma_Function(x)は、 extebdedのxGamma_Functionのランチョス近似で計算されdoubleに変換されます。
xGamma_Function(x)はextendedの精度となります。 exteded
-- longDouble
64ビットでコンパイルすると xGamma_Function(x) はdoubleの精度になります。
通常精度doubleのgamma(x)プログラムでは、0.5より小さい場合 Γ(x)=
π/sin(π/x)Γ(1-x)のΓ(1-x)をランチョス近似で計算
0.5より大きい場合はランチョス近似で計算します。
ガンマ関数の詳細は、インターネットで検索してください。
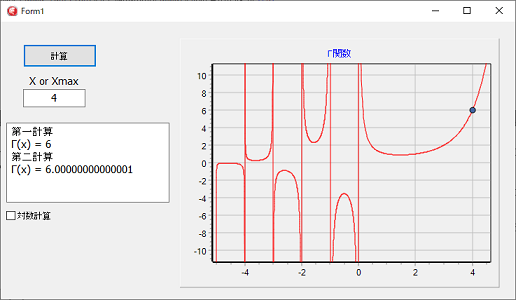Ｘの値-5～171の値を入れる事でΓの値を計算出来ます。
グラフの値は、X軸-5～4.5 Y軸-11から11固定です。
対数計算の時は、値によって変動しますが、Xがマイナスの時は複素数の出力となります。
(値として複素数を扱うのではなく、表示が複素数の表示となります。)
第二計算が、通常精度の計算結果です。
プログラム
プログラムは、少し精度の高い、gamma_function(x)と、通常精度のgamma(x)の計算があります。
gamma_function(x)はX86モード(32ビット)の計算にあわせてありX86モード(32ビット)の時はgamma_function(x)の方が精度が高くなりますが、X64(64ビット)のモードではgamma(x)の方が精度が高くなります。
//============================================================================= // http://www.mymathlib.com/c_source/functions/gamma_beta/gamma_function.c // // ルーチン // Gamma_Function // xGamma_Function // Gamma_Function_Max_Arg // xGamma_Function_Max_Arg // // 実数x> 0のxのガンマ関数は次のように定義されます。 // Gamma(x)= Integral[0、inf]t^(x-1)exp(-t)dt // 複雑な平面内で解析的に継続され、単純な極がある // 非正の整数、つまりガンマ関数は有理型である // 非正の整数に単純な極を持つ関数。 // 実数x<0の場合、ガンマ関数は反射方程式を満たします。 // Gamma(x)= pi/(sin(pi*x)*Gamma(1-x)) // // 関数Gamma_Function()およびxGamma_Function()はガンマを返します。 // 関数はxでx実数で評価されます。 // // 関数Gamma_Function_Max_Arg()は、最大引数を返します // 引数>1のガンマ関数は、double型の値を返します。 // // 関数xGamma_Function_Max_Arg()は、 // 引数>1のガンマ関数とextended型の戻り値です。 // //============================================================================= unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart, system.UITypes; type TForm1 = class(TForm) Button1: TButton; Chart1: TChart; Series1: TLineSeries; LabeledEdit2: TLabeledEdit; Memo1: TMemo; Series2: TPointSeries; CheckBox1: TCheckBox; procedure Button1Click(Sender: TObject); private { Private 宣言 } function Gamma_Function(x: double): double; function xGamma_Function(x: extended): extended; function xGamma(x: extended): extended; function Duplication_Formula(two_x: extended): extended; function Gamma_Function_Max_Arg: double; function xGamma_Function_Max_Arg: extended; function Ln_Gamma_Function(x: double): double; function xLn_Gamma_Function(x: extended): extended; function xLnGamma_Asymptotic_Expansion(x: extended): extended; function gamma(z: double): double; function maxarg: double; public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses math; const LONG_MAX = 2147483647; e = 2.71828182845904523536028747; exp_g_o_sqrt_2pi = 6.23316569877722552586386e+3; g = 9.65657815377331589457187; max_double_arg: double = 171.6243769; max_long_double_arg: extended = 1755.5; a: array[0..8] of extended = ( +1.14400529453851095667309e+4, -3.23988020152318335053598e+4, +3.50514523505571666566083e+4, -1.81641309541260702610647e+4, +4.63232990536666818409138e+3, -5.36976777703356780555748e+2, +2.28754473395181007645155e+1, -2.17925748738865115560082e-1, +1.08314836272589368860689e-4 ); //============================================================================= // // この関数はLanczosの式を使用して実際のGamma(x)を計算します。 // xの範囲は -(max_double_arg-1) < x < max_double_arg。 // ガンマ関数は複素平面で有理型であり、 // 正でない整数の値、xaの正の整数または半分の正の整数をテストすると、 // 約1.9e-16の最大絶対相対誤差です。 // x > max_double_argの場合、xGamma_Function(x)を使用する必要があります。 // または lnGamma(x) を計算します。 // x < 0の場合、ln(Gamma(x))は複素数になる可能性があることに注意してください。 // 複素数の計算はプログラムに組んでありません // 戻り値 // xが正で、max_double_argより小さい場合、Gamma(x)は // 返され、x> max_double_argの場合、maxdoubleが返されます。 // xが非正の整数、つまりxが極の場合、maxdoubleが返されます。 // （Gamma(x)は極の両側で符号を変更することに注意してください）。 // xが非正の非整数の場合 Gamma(x)> maxdouble場合、maxdoubleが返され、 // Gamma(x)<-maxdoubleの場合、-maxdoubleが返されます。 // //============================================================================= //================ ガンマ関数 =================== // Γ(x) function TForm1.Gamma_Function(x: double): double; var g: extended; maxx: double; begin maxx := max_double_arg; if x > maxx then begin result := maxdouble; exit; end; g := xGamma_Function(x); if abs(g) < maxdouble then result := g else if g < 0 then result := -maxdouble else result := maxdouble; end; //============================================================================= // // この関数はLanczosの式を使用して実際のGamma(x)を計算します。 // xの範囲は -(max_long_double_arg-1) < x < max_long_double_arg。 // ガンマ関数は複素平面で有理型であり、正でない整数の値 // xaの正の整数または半分の正の整数をテストすると、 // 最大絶対相対誤差は約3.5e-16です。 // // x > max_long_double_argの場合、lnGamma(x)を使用する必要があります。 // x < 0 の場合、ln(Gamma(x)) は複素数になる可能性があることに注意してください。 // // 戻り値 // xが正で、max_long_double_argより小さい場合、Gamma(x) // が返され、x > max_long_double_argの場合、maxextendedが返されます。 // xが正でない整数の場合、maxextendedが // 返されます（Gamma(x)は値の両側で符号を変更することに注意してください）。 // xが非正の非整数の場合でx>-(max_long_double_arg + 1）の場合 // Gamma(x)が返されます。それ以外の場合は0.0が返されます // //============================================================================= function TForm1.xGamma_Function(x: extended): extended; var sin_x: extended; rg: extended; ix: int64; begin if x > 0 then if x <= max_long_double_arg then begin result := xGamma(x); exit; end else begin result := maxextended; exit; end; if x > -LONG_MAX then begin ix := round(x); if x = ix then begin result := maxextended; exit; end; end; sin_x := sin(pi * x); if sin_x = 0 then begin result := maxextended; exit; end; if x < - max_long_double_arg - 1 then begin result := 0; exit; end; rg := xGamma(1 - x) * sin_x / pi; if rg <> 0 then result := 1 / rg else result := maxextended; end; //============================================================================= // // この関数はLanczosの式を使用して実際のGamma(x)を計算します。 // x、ここで0<x<=900。900<x<1755.5の場合、倍数公式を使用します。 // 関数power()。結果の相対誤差は約10^-16です。x = 0付近を除きます。 // x>1755.5の場合、lnGamma(x)を計算する必要があります。 // xが正で1755.5未満の場合、Gamma(x)が返され、 // x>1755.5の場合、maxextendedが返されます。 // //============================================================================= function TForm1.xGamma(x: extended): extended; var xx: extended; temp: extended; n, i: integer; xx2 : extended; begin if x < 1 then xx := x + 1 else xx := x; n := sizeof(a) div sizeof(extended); if x > max_long_double_arg then begin result := maxextended; exit; end; if x > 900 then begin result := Duplication_Formula(x); exit; end; temp := 0; for i := n - 1 downto 0 do temp := temp + a[i] / (xx + i); temp := temp + 1; temp := temp * (power((g + xx - 0.5) / e, xx2) / exp_g_o_sqrt_2pi ); temp := temp * power((g + xx - 0.5) / e, xx2); if x < 1 then result := temp / x else result := temp; end; //============================================================================= // // この関数は倍数公式を使用してGamma(two_x)を返します。 // //============================================================================= function TForm1.Duplication_Formula(two_x: extended): extended; var x: extended; g: extended; n: integer; begin x := 0.5 * two_x; n := round(two_x) - 1; g := power(2.0, two_x - 1.0 - n); g := g * power(2, n); g := g / sqrt(pi); g := g * xGamma_Function(x); g := g * xGamma_Function(x + 0.5); result := g; end; //============================================================================= // // この関数は、Gamma_Functionの最大引数を返します。 // Gamma_Functionは引数が1より大きい場合、< maxdoubleという数値が返されます。 // //============================================================================= function TForm1.Gamma_Function_Max_Arg: double; begin result := max_double_arg; end; //============================================================================= // // この関数は、xGamma_Functionの最大引数を返します。 // xGamma_Functionは引数が1より大きい場合、< maxextendedという数値が返されます。 // //============================================================================= function TForm1.xGamma_Function_Max_Arg: extended; begin result := max_long_double_arg; end; //***************************************************************************** //============================================================================= // // 正の実数xに対するGamma(x)の自然対数を計算します。 // //============================================================================= //============================================================================= // Ln_Gamma_Function(x) および xLn_Gamma_Function(x) // // Gamma_Function_Max_Arg = 171とすると、 // 0 < x <= 171の場合、ln(gamma(x))は、Gamma_Function(x)からの結果。 // x> 171の場合、ln(gamma(x)は漸近展開を使用して計算されます。 // ln(gamma(x)〜ln(2sqrt(2pi))-x + (x-1/2)ln x + // B[2j] / [2j *(2j-1)* x^(2j-1)]の合計、 // 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。 // //============================================================================= function TForm1.Ln_Gamma_Function(x: double): double; begin // 正の引数の 0 <x <= Gamma_Function_Max_Arg // の場合、Log(Gamma(x)を返します。 if x <= Gamma_Function_Max_Arg then result := ln(Gamma_Function(x)) //そうでない場合は、ln Gamma(x) の漸近展開から結果を返します。 else result := xLnGamma_Asymptotic_Expansion(x); end; //============================================================================= // // 正の実数のGamma(x)の自然対数を計算します // // Gamma_Function_Max_Arg = 171とすると、 // 0 <x <= 171の場合、ln(gamma(x))は // Gamma_Function(x)からの結果の値。 // x> 171の場合、ln(gamma(x)) は漸近展開を使用して計算されます。 // ln（gamma(x))〜ln（2sqrt(2pi))-x +(x-1/2)ln x + // B[2j] / [2j *(2j-1)* x^(2j-1)]の合計、 // 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。 // //============================================================================= function TForm1.xLn_Gamma_Function(x: extended): extended; begin // 正の引数の場合、0 <x <= Gamma_Function_Max_Arg() // の場合、LogGamma(x)を返します。 if x <= xGamma_Function_Max_Arg then result := ln(xGamma_Function(x)) // そうでない場合は、ln Gamma(x) の漸近展開から結果を返します。 else result := xLnGamma_Asymptotic_Expansion(x); end; //============================================================================= // // この関数は、漸近を評価することでlog(gamma(x)を推定します // // ln(Gamma(x))〜ln(2sqrt(2pi))-x +(x-1/2)ln(x) + // B[2j] / [2j *（2j-1）* x^(2j-1)]の合計、 // 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。 // //============================================================================= const log_sqrt_2pi = 9.18938533204672741780329736e-1; //ベルヌーイ数B(2)、B(4)、B(6)、...、B(20)現在B(2)、...、B(6)のみ B : array[0..9] of extended = ( 1.0 / (6 * 2 * 1), -1.0 / (30 * 4 * 3), 1.0 / (42 * 6 * 5), -1.0 / (30 * 8 * 7), 5.0 / (66 * 10 * 9), -691.0 / (2730 * 12 * 11), 7.0 / (6 * 14 * 13), -3617.0 / (510 * 16 * 15), 43867.0 / (798 * 18 * 17), -174611.0 / (330 * 20 * 19)); n: integer = sizeof(B) div sizeof(extended); function TForm1.xLnGamma_Asymptotic_Expansion(x: extended): extended; //const // m = 3; // 3で十分な精度が得られます。 var i : integer; term: array[0..9] of extended; sum : extended; xx : extended; xj : extended; lngamma : extended; begin sum := 0; xx := x * x; xj := x; lngamma := log_sqrt_2pi - xj + (xj - 0.5) * ln(xj); for i := 0 to n - 1 do begin // for i := 0 to m - 1 do begin term[i] := B[i] / xj; xj := xj * xx; end; for i := n - 1 downto 0 do sum := sum + term[i]; // for i := m - 1 downto 0 do sum := sum + term[i]; result := lngamma + sum; end; //***************************************************************************** //============================================================================= // // Lanczosの近似式 // gamma(z)の計算はGamma_Function(x)より精度は悪いが実際の計算においては // 十分な精度と思われます。 // プログラムが小さくて済みます。 // //============================================================================= function TForm1.maxarg: double; const max_double_zx: double = 171.6243769; begin result := max_double_zx; end; function TForm1.gamma(z: double): double; const P: array[0..7] of double = ( 676.5203681218851, -1259.1392167224028, 771.32342877765313, -176.61502916214059, 12.507343278686905, -0.13857109526572012, 9.9843695780195716e-6, 1.5056327351493116e-7); max_double_z: double = 171.0; var i : integer; a, t : double; maxz: double; zp2 : double; begin if z <= 0 then begin i := round(z); if i = z then begin result := maxDouble; exit; end; end; maxz := maxarg; if z > maxz then begin result := maxdouble; exit; end; if z < 0.5 then begin result := pi / (sin(pi * z) * gamma(1 - Z)); exit; end; z := z - 1; a := 0.99999999999980993; for i := 0 to length(p) - 1 do a := a + p[i] / (z + i + 1); t := z + length(p) - 0.5; result := sqrt(2 * pi) * power(t, zp2) * exp(-t) * a; result := result * power(t, zp2); end; //***************************************************************************** //============================================================================= // ガンマ関数計算 // グラフは、０及び負の整数値を避けてグラフを作成します。 // グラフのXの値は-5～4.5の範囲です。 // 入力されたXの値でガンマ関数を計算し、グラフのΓ曲線上にプロットします。 //============================================================================= procedure TForm1.Button1Click(Sender: TObject); const GLIMIT = 100; // グラフデーター上下限値 グラフ値のオーバーフロー防止数 PLIMIT = 11.3; // グラフ点プロットの上下限値点の半分を表示 ALIMIT = 10.5; // 通常Γ値グラフ左軸スケール上下値 MINARG = 5.5626846463e-309; // 下限値 0 < x MINARG でオーバーフロー var ch : integer; X, G, G0 : extended; dx : double; Xs : double; XE, GE : extended; maxarg0: extended; Sg : string; istr : string; FINF : boolean; FLIMIT : Extended; XD : double; X8664F : boolean; // true 86 false 64 procedure Gamma_Graph(Min, Max: double); const NM = 100; var i : integer; begin dx := (Max - Min) / NM; for i := 0 to NM do begin Xs := dx * i + Min; if i = NM then Xs := Xs - 1E-12; if i = 0 then Xs := Xs + 0.1E-12; if checkbox1.Checked = False then G := Gamma_Function(Xs) else begin if Xs >= 0 then G := Ln_Gamma_Function(Xs); else begin G := Gamma_Function(Xs); G := Ln(abs(G)); end; end; if (checkbox1.Checked = True) and (X < 0) then begin if G > ALIMIT then G := ALIMIT; end; if G > FLIMIT then G:= FLIMIT + 1; if G < -GLIMIT then G := -GLIMIT; Series1.AddXY(Xs, G); end; end; begin val(LabeledEdit2.Text, X, Ch); if ch <> 0 then begin MessageDlg('X値に間違いがあります。', mtInformation, [mbOk], 0, mbOk); exit; end; if abs(X) < MINARG then X := 0; // 0< X <MINARG でオバーフロー istr := ''; if (checkbox1.Checked = True) and (X < 0) then // 対数計算で値xがゼロ以下になら istr := ' -' + floatTostr(pi * (abs(trunc(x)) + 1)) + 'i' + #13#10 + '答えは複素数です'; val(LabeledEdit2.Text, XE, Ch); // extended xe 値セット Series1.Clear; Series2.Clear; Memo1.Clear; Sg := 'Γ(x) = '; GE := 0; FINF := False; FLIMIT := GLIMIT; if checkbox1.Checked = true then begin FLIMIT := ALIMIT; Sg := 'LnΓ(x) = '; end; {$IFDEF CPUX64} // プラットフォーム64ビット begin X8664F := False; Memo1.Lines.Add('X64モード'); end; {$ENDIF CPUX64} {$IFDEF CPUX86} // プラットフォーム32ビット begin X8664F := True; Memo1.Lines.Add('X86モード'); end; {$ENDIF CPUX86} Memo1.Lines.Add('第一計算'); if X8664F then maxarg0 := xGamma_Function_Max_Arg // ガンマ計算の最大値 else maxarg0 := Gamma_Function_Max_Arg; if (XE <= 0) and (round(XE) = XE) then begin // 値が負の整数なら Memo1.Lines.Add(Sg + '∞'); FINF := True; // ∞フラグセット end else begin // 負の整数でないなら if checkbox1.Checked = False then begin // 非対数なら if X8664F then GE := xGamma_Function(XE) else GE := Gamma_Function(X); end else // 対数なら if XE >= 0 then begin // 値がゼロより大きかったら if X8664F then GE := xLn_Gamma_Function(XE) // 対数ガンマ else GE := Ln_Gamma_Function(XE) end else begin // 値がマイナスなら if X8664F then GE := xGamma_Function(XE) // ガンマ else GE := Gamma_Function(XE); GE := Ln(abs(GE)); // 絶対値の対数 end; if checkbox1.Checked = false then begin // 対数計算でないなら if X > maxarg0 then // 計算の最大値チェック Memo1.Lines.Add('入力値が計算最大値を超えています。') else Memo1.Lines.Add(Sg + floatTostr(GE) + istr); // GEの値表示 end else Memo1.Lines.Add(Sg + floatTostr(GE) + istr); // GEの値表示 end; Memo1.Lines.Add('第二計算'); if (X <= 0) and (round(X) = X) then begin memo1.Lines.Add(Sg + '∞') end else begin G0 := Gamma(X); if checkbox1.Checked = true then G0 := Ln(abs(G0)); maxarg0 := maxarg; if x >= maxarg0 then Memo1.Lines.Add('入力値が計算最大値を超えています。') else Memo1.Lines.Add(Sg + floatTostr(G0) + istr); end; // グラフ表示 if checkbox1.Checked = False then begin // 通常Γ値の場合 if GE < MAXDOUBLE / 2 then begin if GE > FLIMIT then FLIMIT := GE + GE / 2; end else FlIMIT := 1E15; if X >= 0 then begin if GE > 1E15 then Begin FLIMIT := 1E15; GE := FLIMIT - FLIMIT / 32; end; end else begin FLIMIT := 10; if GE > FLIMIT then FLIMIT := GE + GE / 2; end; chart1.LeftAxis.Automatic := False; // グラフ左軸スケール固定 if Chart1.LeftAxis.Minimum >= -ALIMIT then begin // グラフ左軸スケール上下限設定 Chart1.LeftAxis.Minimum := -ALIMIT; Chart1.LeftAxis.Maximum := FLIMIT - FLIMIT / 14; end else begin Chart1.LeftAxis.Maximum := FLIMIT - FLIMIT / 14; Chart1.LeftAxis.Minimum := -ALIMIT; end; if GE > FLIMIT then GE := FLIMIT; // 上限値にカット if GE < -PLIMIT then GE := -PLIMIT; // 可限値にカット if not FINF then Series2.AddXY(X, GE); // GEの値グラフ追加 カット値 // グラフ作成 XD := round(X); if X > 0 then begin Gamma_Graph(0, X + 2); end else begin if XD > -4 then begin Gamma_Graph(-4, -3); Gamma_Graph(-3, -2); Gamma_Graph(-2, -1); Gamma_Graph(-1, -0); Gamma_Graph(0, X + 2); end else begin Gamma_Graph(XD - 2, XD - 1); Gamma_Graph(XD - 1, XD); Gamma_Graph(XD , XD + 1); Gamma_Graph(XD + 1, XD + 2); Gamma_Graph(XD + 2, XD + 3); end; end; end else begin // 対数Γ値計算時 if GE > FLIMIT then FLIMIT := GE + GE * 2; // グラフ作成 chart1.LeftAxis.Automatic := True; // グラフ左軸スケール自動 if not FINF then Series2.AddXY(X, GE); if X < 2 then Gamma_Graph(round(x) - 2, round(x) + 2) else Gamma_Graph(0.1 , round(x) + 3) end; end; end.
次のプログラムは、対数のΓ関数を計算して、expで通常の値に変換するプログラムです。
対数のΓ関数を計算することにより、ベルヌーイ数を使用して計算が出来るので、多倍長演算を利用して、精度の高い計算も可能となります。
上記のプログラムにも、対数のガンマ関数の計算があるのですが、値が大きい時だけ、ベルヌーイ数を利用して、対数のΓ関数を計算しています。
下記のプログラムは、与えられた値Xが、ベルヌーイ数の数より小さい時は、値の補正をしています。
対数のΓ関数の計算パターンを三個ほど用意しましたが、計算は全て同じ計算をしています、計算手順により誤差が変化するのを確認する為です。
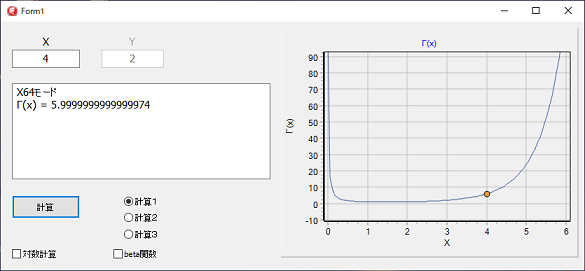
x86(32ビット)モードの時はExtendedで計算されx64(64ビット)モードの時はDoubleで計算されます。
Double時で15桁の精度で計算されるので上記のプログラムと同等なので、プログラムに組み込む場合は、下記のプログラムの何れかのガンマ計算を組み込めば良いでしょう。
xの値が小さい時の補正として次の計算が組み込まれていますが、ベルヌーイ数の数と、求めたい精度によって、ループ数を調整します。
while x < m do begin
v := v * x;
x := x + 1;
end;
下記のプログラムではループ数をベルヌーイ数の数にあわせてありますがこの値は、Extendedの精度にあわせてあります。
同じ精度で、ベルヌーイ数を増やした場合は、補正用のループ数を減らすことが出来ます。
ベルヌーイ数を減らした場合は、補正用のループ数を増やして補正値を大きくすれば、同じ精度を出すことが出来ますが、いくら大きくしても、浮動小数点の演算精度より精度を上げることは出来ません。
大きくし過ぎると、逆に計算精度が落ちてしまいます。
ベルヌーイ数の数と、補正用計算のバランスをとり、効率よく高い精度で計算させる必要があります。
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, system.Math, VclTee.TeeGDIPlus,
VCLTee.Series, VCLTee.TeEngine, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart,
Vcl.StdCtrls, system.UITypes;
type
TForm1 = class(TForm)
Button1: TButton;
LabeledEdit1: TLabeledEdit;
Memo1: TMemo;
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
CheckBox1: TCheckBox;
LabeledEdit2: TLabeledEdit;
CheckBox2: TCheckBox;
RadioButton1: TRadioButton;
RadioButton2: TRadioButton;
RadioButton3: TRadioButton;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure CheckBox2MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
const
//ベルヌーイ数B(2)、B(4)、B(6)、...、B(20)
B : array[1..10] of extended = ( 1.0 / 6, // B(2)
-1.0 / 30,
1.0 / 42,
-1.0 / 30,
5.0 / 66,
-691.0 / 2730,
7.0 / 6,
-3617.0 / 510,
43867.0 / 798,
-174611.0 / 330); // B(20)
m: integer = sizeof(B) div sizeof(extended);
//************** 計算3 ***********************
function LnGamma(x: extended): extended; // ガンマ関数の対数
var
i : integer;
sum : extended;
xx, v : extended;
ln_sqrt_2pi: extended;
m : integer;
begin
m := 10; // ベルヌーイ数適用テスト用
ln_sqrt_2pi := ln(sqrt(2 * pi)); // = ln(2 * pi) / 2;
sum := 0;
v := 1;
while x < m do begin
v := v * x;
x := x + 1;
end;
xx := 1 / (x * x);
for i := m downto 2 do
sum := (sum + B[i] / (i * 2 * (2 * i - 1))) * xx;
result := (sum + B[1] / 2) / x
+ ln_sqrt_2pi - ln(v) - x + (x - 0.5) * ln(x);
end;
//*************** 計算2 *************************
function xLnGamma(x: extended): extended; // ガンマ関数の対数
var
i : integer;
sum : extended;
xx, v : extended;
xj : extended;
lng : extended;
ln_sqrt_2pi: extended;
begin
ln_sqrt_2pi := ln(sqrt(2 * pi)); // = ln(2 * pi) / 2;
sum := 0;
v := 1;
while x < m do begin
v := v * x;
x := x + 1;
end;
xx := x * x;
xj := x;
lng := ln_sqrt_2pi - x + (x - 0.5) * ln(x) - ln(v);
for i := 1 to m do begin
sum := sum + B[i] / (i * 2 * (2 * i - 1)) / xj;
xj := xj * xx;
end;
result := sum + lng;
end;
//****************** 計算1 ***************************
function loggamma(x: extended): extended; // ガンマ関数の対数
var
log_2pis2 : extended;
v, w: extended;
begin
log_2pis2 := ln(2 * pi) / 2;
v := 1;
while x < 10 do begin // ベルヌーイ数の数によりx値が小さい時補正します
v := v * x;
x := x + 1;
end;
w := 1 / (x * x);
result := (((((((((
B[10] / (20 * 19) * w + B[9] / (18 * 17)) * w
+ B[8] / (16 * 15)) * w + B[7] / (14 * 13)) * w
+ B[6] / (12 * 11)) * w + B[5] / (10 * 9)) * w
+ B[4] / ( 8 * 7)) * w + B[3] / ( 6 * 5)) * w
+ B[2] / ( 4 * 3)) * w + B[1] / ( 2 * 1)) / x
+ log_2pis2 - ln(v) - x + (x - 1 / 2) * ln(x);
end;
//--------------------------------------------------------------
function log_Gamma(x: extended): extended; // ガンマ選択
begin
result := 0;
if form1.RadioButton1.Checked = True then result := logGamma(x);
if form1.RadioButton2.Checked = True then result := xLnGamma(x);
if form1.RadioButton3.Checked = True then result := LnGamma(x);
end;
function gamma(x: extended): extended; // ガンマ関数
begin
if x < 0 then begin
result := pi / (sin(pi * x) * exp(log_Gamma(1 - x)));
end
else begin
result := exp(log_Gamma(x));
end;
end;
function beta(x, y: extended): extended; // ベータ関数
begin
result := exp(log_Gamma(x) + log_Gamma(y) - log_Gamma(x + y));
end;
//-------------------------------------------------------------------------
procedure TForm1.Button1Click(Sender: TObject);
const
GLIMIT = 100; // グラフデーター上下限値 グラフ値のオーバーフロー防止数
PLIMIT = 11.3; // グラフ点プロットの上下限値点の半分を表示
ALIMIT = 10.5; // 通常Γ値グラフ左軸スケール上下値
MAXARG = 171.6243769; // double 時 最大値
EXMAXARG = 1755.5; // extended 時 最大値
MINARG = 2.22507e-308; // double 時 最小値
EXMINARG = 3.3621e-4932; // extended 時最小値
var
ch : integer;
X, G, Y : extended;
dx : extended;
Xs : extended;
istr : string;
Sg : string;
FLIMIT, MLINIT : extended;
XD : extended;
MAXARGE : extended;
MINARGE : extended;
procedure Gamma_Graph(Min, Max: double);
const
NM = 100;
var
i : integer;
G : double;
begin
if Max > MAXARG then Max := MAXARG;
dx := (Max - Min) / NM;
for i := 0 to NM do begin
Xs := dx * i + Min;
if i = NM then Xs := Xs - 1E-12;
if i = 0 then Xs := Xs + 0.1E-12;
if checkbox1.Checked = false then
G := Gamma(Xs)
else begin
if Xs > 0 then
G := log_Gamma(Xs)
else
G := ln(abs(gamma(Xs)));
end;
if G > FLIMIT then G := FLIMIT + 1;
if G < -GLIMIT then G := -GLIMIT;
Series1.AddXY(Xs, G);
end;
end;
begin
Memo1.Clear;
{$IFDEF CPUX64} // プラットフォーム64ビット
begin
MAXARGE := MAXARG;
MINARGE := MINARG;
Memo1.Lines.Add('X64モード');
end;
{$ENDIF CPUX64}
{$IFDEF CPUX86} // プラットフォーム32ビット
begin
Memo1.Lines.Add('X86モード');
MAXARGE := EXMAXARG;
MINARGE := EXMINARG;
end;
{$ENDIF CPUX86}
val(LabeledEdit1.Text, X, Ch);
if ch <> 0 then begin
MessageDlg('X値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
if X > MAXARGE then begin
MessageDlg('Xの値が大きすぎます。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
if abs(X) < MINARGE then X := 0; // 0< X <MINARG でオバーフロー
Series1.Clear;
Series2.Clear;
if checkbox2.Checked = true then begin
val(LabeledEdit2.Text, Y, Ch);
if ch <> 0 then begin
MessageDlg('Y値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
if Y > MAXARGE then begin
MessageDlg('Yの値が大きすぎます。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
if X <= 0 then begin
MessageDlg('X値の値はゼロ以上にして下さい。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
if Y <= 0 then begin
MessageDlg('Y値の値をゼロ以上にして下さい。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
G := beta(X, Y);
Memo1.Lines.Add('Beat' + '(' + floatTostr(X) + ',' + floatTostr(Y) +') = ' + floatTostr(G));
// β(x,y) グラフ表示
chart1.LeftAxis.Automatic := True; // グラフ左軸スケール自動
Series2.AddXY(X, G);
MLIMIT := X / 2;
FLIMIT := X * 2;
dx := (FLIMIT - MLIMIT) / 100;
for ch := 0 to 100 do begin
X := MLIMIT + dx * ch;
G := beta(X, Y);G := beta(X, Y);
Series1.AddXY(X, G);
end;
chart1.BottomAxis.Title.Text := 'X';
chart1.LeftAxis.Title.Text := 'β(x,y)';
chart1.Title.Text.Clear;
chart1.Title.Text.Add('β(x,y)');
exit;
end;
istr := '';
if (checkbox1.Checked = True) and (X < 0) then // 対数計算で値xがゼロ以下になら
istr := ' -' + floatTostr(pi * (abs(trunc(x)) + 1)) + 'i' + #13#10 + '答えは複素数です';
FLIMIT := GLIMIT;
Sg := 'Γ(x) = ';
// グラフ表示
Chart1.Title.Text.Text := 'Γ(x)';
if (X <= 0) and (round(X) = X) then begin // 値が負の整数なら
Memo1.Lines.Add(Sg + '∞');
end
else begin
if checkbox1.Checked = false then
G := Gamma(X)
else begin
if X > 0 then G := log_Gamma(X)
else G := ln(abs(Gamma(X)))
end;
Memo1.Lines.Add(Sg + floatTostrF(G, ffgeneral, 20, 3) + istr);
if G < MAXDOUBLE / 2 then begin
if G > FlIMIT then FlIMIT := G + G / 2;
end;
if X >= 0 then begin
if G > 1E15 then Begin
FLIMIT := 1E15;
G := FLIMIT - FLIMIT / 32;
end;
end
else begin
FLIMIT := 10;
if G > FLIMIT then FLIMIT := G + G / 2;
end;
chart1.LeftAxis.Automatic := False; // グラフ左軸スケール固定
if Chart1.LeftAxis.Minimum >= -ALIMIT then begin // グラフ左軸スケール上下限設定
Chart1.LeftAxis.Minimum := -ALIMIT;
Chart1.LeftAxis.Maximum := FLIMIT - FLIMIT / 14;
end
else begin
Chart1.LeftAxis.Maximum := FLIMIT - FLIMIT / 14;
Chart1.LeftAxis.Minimum := -ALIMIT;
end;
if G < Chart1.LeftAxis.Minimum then G := Chart1.LeftAxis.Minimum;
if G > Chart1.LeftAxis.Maximum then G := Chart1.LeftAxis.Maximum;
Series2.AddXY(X, G);
end;
// グラフ作成
XD := round(X);
if X > 0 then begin
Gamma_Graph(0, X + 2);
end
else begin
if XD > -4 then begin
Gamma_Graph(-4, -3);
Gamma_Graph(-3, -2);
Gamma_Graph(-2, -1);
Gamma_Graph(-1, 0);
Gamma_Graph( 0, 1);
end
else begin
Gamma_Graph(XD - 2, XD - 1);
Gamma_Graph(XD - 1, XD);
Gamma_Graph(XD , XD + 1);
Gamma_Graph(XD + 1, XD + 2);
Gamma_Graph(XD + 2, XD + 3);
end;
end;
end;
procedure TForm1.CheckBox2MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
if CheckBox2.Checked = true then begin
Labelededit2.Enabled := true;
CheckBox1.Enabled := false;
end
else begin
Labelededit2.Enabled := false;
CheckBox1.Enabled := true;
end;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
labelededit2.Enabled := false;
end;
end.
Gamma_function.zip