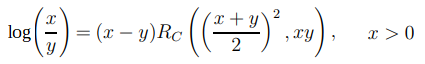
log function
自然対数関数のプログラムのついての検討
自然対数の計算は、カールソンの楕円積分RCを使用する方法と、テーラー展開を使用する方法があります。
RCを使用する場合
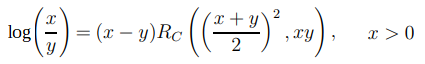
y=1とすれば
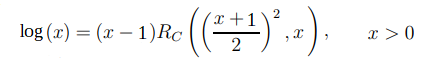
となり
x だけ与えれば:計算出来ます。
計算出来る範囲は、1e-26~1e62位となります。
テーラー展開を使用する場合
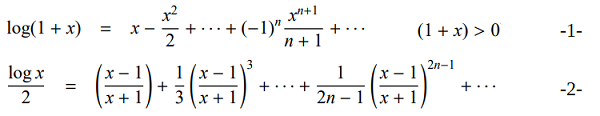
-1-がテーラー展開した場合ですが、このまゝでは、収束性が悪いので、計算式を変換した-2-の展開を使用します。
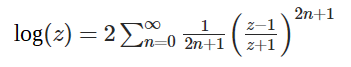
積分の上限が∞となっているので、どこかで計算を打ち切る必要があります、収束の判定は
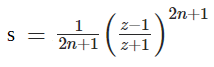
sの計算をn=0からの値が大きくなるとsの値が小さくなるので、Σの値が、桁落ちにより変化しなくなったところで計算を打ち切ります。
計算出来る範囲は、1e-4~1e4位となります。
RCの計算の方が計算出来る値の範囲は広いですが、一般の計算の中で使用するには、計算出来る値の範囲が狭すぎます。
Doubleの値では、1.79769e308の値が最大値です、多倍長の場合もっと大きな値となりますので、次の様にします。
x = m * 2n
log(x)
= log(2) * n + log(m)
mの値が1だとlog(m)の値は0であり、演算時間が一番短くなるので、上記の場合はmの値が0.5~1になるように、nの値を選びます。
xの値が1より小さい場合、nの値は-になりますが、プログラムは、xの値の逆数をとり、nの値を+として計算後、-に変換する方が除算の数を減らす事が出来ます。
次に更に改良して、1前後の値になるようにします。
x / √2 = p * 2n
(p = 0.5~1)
m = x / 2n
log(x) = log(2) * n + log(m)
これでmの値が、0.71~1.41の範囲(1前後)になり効率よく自然対数の計算が出来るよなります。
√2の値の値は、近似値でも問題ありません。
2nの値は、整数1の値をシフトして値を設定します、左シフト数がnの値です。
通常の演算では、int64で64ビットが最大値ですが、ここではbigintegerを使用するので、可成り大きな値まで可能です。
xの値が1より値が小さい場合、例えば1e-5、2e-12
等の場合、2nは、整数のシフトでは表すことが出来ないので、xの値の逆数をとって、1より大きい値として2nの値を計算後、n
= -n + 1とすれば、2nの値(nは負数)を得ることが出来ます。
biginteger,bigDecimalの組み込みはベルヌーイ数 その4を参照してください。
複素数の対数計算は、対数計算(複素数)を参照して下さい。
プログラム
log.pas
// 有効桁数が1000桁程度迄でそれを超えると、演算が非常に遅くなります。 // 有効桁数100桁程度であれば問題ありません。 // 2500桁位が上限です、それ以上必要な場合は収束ループの上限設定を外して下さい。 // 64ビットでコンパイルしないと演算が遅くなります。 unit log; interface uses Velthuis.Bigdecimals, System.SysUtils, Vcl.Forms, Velthuis.BigIntegers; //uses Velthuis.Bigdecimals, System.SysUtils, Vcl.Forms, Velthuis.BigIntegers, main; function log_big(xi: bigdecimal; lf: byte): bigdecimal; function Log_11(x: bigdecimal; dpcs: integer; var ans: bigdecimal): boolean; implementation // カールソンの楕円積分 RC // // ---------------- RC --------------------------------------------------------- // 有効桁数 2500でloop数m 693程度 // x,y 実数 // y <> 0 function RC(x, y: bigdecimal): bigdecimal; label Ext; //const // r = 1E-24; // Qc = 872; // power(3 * r, -1 / 8) = 871.68554 // c1 = 3 / 10; // c2 = 1 / 7; // c3 = 3 / 8; // c4 = 9 / 22; // c5 = 159 / 208; // c6 = 9 / 8; var xt, yt, w, yb, zero : bigdecimal; lamda, A0, Q, dp : bigdecimal; s, Am, Qm : bigdecimal; c, c1, c2, c3, c4, c5, c6, Qc : bigdecimal; m, dpcm, dpcm2 : integer; d1, d2, d3, d4, d7, d8, d9, d10, d22, d159, d208: bigdecimal; begin dpcm := BigDecimal.DefaultPrecision; dpcm2 := dpcm + dpcm; dp := '1E-' + intTostr(round(dpcm / 6)); // 有効桁数から収束判定係数dp=1e-**設定 zero := '0'; if y = zero then begin result := zero; exit; end; d1 := '1'; d2 := '2'; d3 := '3'; d4 := '4'; d7 := '7'; d8 := '8'; d9 := '9'; d10 := '10'; d22 := '22'; d159 := '159'; d208 := '208'; c1 := d3 / d10; c2 := d1 / d7; c3 := d3 / d8; c4 := d9 / d22; c5 := d159 / d208; c6 := d9 / d8; Qc := d1 / dp; // 収束判定係数 Qc=1/dp if y > zero then begin xt := x; yt := y; w := d1; end else begin xt := x - y; yt := - y; w := bigdecimal.sqrt(x / xt, dpcm * 2); // sqrt は有効桁数が1/2 end; yb := yt; A0 := (xt + yt + yt) / d3; Am := A0; Q := Qc * bigdecimal.abs(A0 - xt); // 収束判定係数 Q // Q := power(3 * r, -1 / 8) * abs(A0 - xt); m := 0; Qm := d1; repeat lamda := d2 * bigdecimal.sqrt(xt, dpcm2) * bigdecimal.sqrt(yt, dpcm2) + yt; // sqrt は有効桁数が1/2 lamda := lamda.RoundToPrecision(dpcm); xt := (xt + lamda) / d4; yt := (yt + lamda) / d4; Am := (Am + lamda) / d4; Qm := Qm / d4; m := m + 1; until (Qm * Q < bigdecimal.abs(Am)) or (m > 10000); s := (yb - A0) * (Qm / Am); c5 := c5 + s * c6; c5 := c5.RoundToPrecision(dpcm); c4 := c4 + s * c5; c4 := c4.RoundToPrecision(dpcm); c3 := c3 + s * c4; c3 := c3.RoundToPrecision(dpcm); c2 := c2 + s * c3; c2 := c2.RoundToPrecision(dpcm); c1 := c1 + s * c2; c1 := c1.RoundToPrecision(dpcm); c := c1 * s * s + d1; c := c.RoundToPrecision(dpcm); Am := bigdecimal.sqrt(Am, dpcm * 2); // sqrt は有効桁数が1/2 result := w * (c / Am); result := result.RoundToPrecision(dpcm); // Form1.Memo1.Lines.Append(intTostr(m)); // s := (yb - A0) / power(4, m) / Am; // result := w * (d1 + s * s * (c1 + s * (c2 + s * (c3 + s * (c4 + s * (c5 + s * c6)))))) / bigdecimal.sqrt(Am); end; // ln(x) // カールソンの楕円積分 RCによる // あまり大きな値は不可 1e62が限度 // 小さな値は1e-26 function log_biga(xi: bigdecimal): bigdecimal; var v, t, e, one, two: Bigdecimal; dpcs : integer; begin dpcs := BigDecimal.DefaultPrecision; // 指定精度 xi := xi.RoundToPrecision(dpcs); one := '1'; two := '2'; v := (xi + one) / two; v := v * v; v := v.RoundToPrecision(dpcs); t := Rc(v, xi); e := xi - one; result := t * e; result := result.RoundToPrecision(dpcs); end; // 小さい値のlog計算 // xi 実数 // dpcs 有効桁数 // ans log値 // 戻り値 Loopオーバーフロー 無し true 有り false // loop制限の無い場合 1e-4~1e4 が計算出来る範囲 // loop制限 5.8e-3 ~1.73e2 (kk=10000の場合) function Log_11(x: bigdecimal; dpcs: integer; var ans: bigdecimal): boolean; const KK = 10000; var one, two, x1, x2, i, s, last: bigdecimal; k : integer; begin result := true; one := '1'; two := '2'; x1 := (x - one) / (x + one); // x1 = (x-1)/(x+1) x2 := x1 * x1; // x1^2 x2 := x2.RoundToPrecision(dpcs); i := one; // i=1 s := x1; // s初期値 k := 0; // 長ループ脱出用カウンタ0 repeat x1 := x1 * x2; // x1^2n+1 x1 := x1.RoundToPrecision(dpcs); i := i + two; // 2n+1 i := i.RoundToPrecision(dpcs); last := s; // 判定用sの値保存 s := s + x1 / i; // Σs = s + x1^2n+1 / (2n+1) s := s.RoundToPrecision(dpcs); // 収束判定の為指定有効桁数以下丸め inc(k); // ループカウンタインクリメント until (last = s) or (k > KK); // 収束判定 ans := two * s; if k > kk then result := false; // Form1.Memo1.Lines.Append(intTostr(k)); end; // x = m * 2^n のnの値と2^nの値を戻します // result = n // ta = 2^n // m = x / 2^n function frexpa(x: bigdecimal; var ta: biginteger): integer; var tb: biginteger; xi, one: bigdecimal; n, j, s, pcs : integer; begin pcs := BigDecimal.DefaultPrecision; one := '1'; one := one.RoundToPrecision(pcs); xi := x; // x保存 if xi < one then x := one / x; // 1より小さかったら逆数 ta := '1'; n := 0; j := 0; // シフト回数クリア ta := '1'; // ta初期値 s := 4096; // s=4^i i = 6 repeat while x > ta do begin biginteger.ShiftLeft(ta, s, tb); // s分左シフト ta := tb; inc(j); // シフト回数インクリメント end; if (s > 1) and (j > 0) then begin // ta > x になったら dec(j); // シフト回数デクリメント biginteger.Shiftright(ta, s, tb); // s分右シフト ta := tb; end; n := n + s * j; // 2^nのn計算 j := 0; // シフト回数クリア s := s shr 2; // sの値を1/4にする 右へ2ビットシフト // s := s div 4; // sの値を1/4にする until s = 0; // s= ...16, 4, 1, 0 if xi < one then begin // より小さかったら n := -n + 1; // 2^nのn値負数 biginteger.Shiftright(ta, 1, tb); // 上式+1により右シフト ta := tb; end; result := n // ta = 2^n end; // loge(x) ln(x) // 級数展開 // 1e±500000 程度が限度 // fl 小さい値のlog計算選択フラグ 0 log11 1 RC // sm <xi< last の範囲外の場合 (0.7~xi~1.4) * 2^nに変換 xiが1に近いほど変換早い function log_bigf(xi: bigdecimal; lf: byte): bigdecimal; label EXT; const KK = 10000; var LOG2, SQRT2, two, last, s, sm, one, one1, k2, a: bigdecimal; k : integer; kb, ta : biginteger; pcsBack, dpcs : integer; rmback : BigDecimal.RoundingMode; begin result := '0'; if xi <= result then begin application.MessageBox('無効な値です。','注意',0); exit; end; if lf = 0 then begin // log11条件設定 sm := '1e-2'; last := '5e1'; end else begin // logRC条件設定 sm := '1e-5'; last := '1e10'; end; pcsBack := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ dpcs := pcsBack + 5; // 指定精度 + α BigDecimal.DefaultPrecision := dpcs; BigDecimal.DefaultRoundingMode := rmNearesteven; one := '1'; if xi = one then begin // result := '0'; // 設定済み goto EXT; end; if (xi > sm) and (xi < last) then begin // 指数の値が小さい場合はRC又はLog11計算 if lf = 0 then begin Log_11(xi, dpcs, a); // log11 result := a; end else result := log_biga(xi); // RC計算 goto EXT; end; one1 := '1e500000'; if xi < one then begin last := one / xi; if last > one1 then begin application.MessageBox('値が小さすぎます。','注意',0); goto EXT; end; end; if xi > one1 then begin application.MessageBox('値が大きすぎます。','注意',0); goto EXT; end; one1 := one.RoundToPrecision(dpcs); two := '2'; if lf = 0 then Log_11(two, dpcs, LOG2) // log(2) else LOG2 := log_biga(two); // log(2) RC SQRT2 := bigdecimal.Sqrt(two, dpcs * 2); // k := frexpa(xi, ta); // x = m * 2^k ta = 2^k k := frexpa(xi / SQRT2, ta); // x / √2 = m * 2^k ta = 2^k kb := k; k2 := ta; // 2^k integer to decimal k2 := k2.RoundToPrecision(dpcs); if k < 0 then begin // kが負数だったら xi := xi * k2; // x * 2^k x=0.707~1.414 √2 xi := xi.RoundToPrecision(dpcs); end else begin xi := xi / k2; // x / 2^k x=0.707~1.414 √2 end; // Form1.Memo1.Lines.Append(xi.ToPlainString); if xi <> one then begin // xi <> 1 なら if lf = 0 then Log_11(xi, dpcs, s) // log(xi) else s := log_biga(xi); // log(xi) RCによる end else s := '0'; // xi=1なら s=0 result := LOG2 * kb + s; // Form1.Memo1.Lines.Append(s.ToPlainString); EXT: result := result.RoundToPrecision(pcsBack); BigDecimal.DefaultPrecision := pcsBack; // 除算演算精度復帰 BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰 end; // log(x) function log_big(xi: bigdecimal; lf: byte): bigdecimal; begin result := log_bigf(xi, lf); end; end.
main,pas
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls, system.Character,
system.Diagnostics;
type
TForm1 = class(TForm)
Memo1: TMemo;
ClearBtn: TBitBtn;
PrecisionEdit: TLabeledEdit;
GroupBox3: TGroupBox;
CalcBtn: TBitBtn;
XinEdit: TLabeledEdit;
Edit1: TEdit;
CheckBox1: TCheckBox;
procedure ClearBtnClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure CalcBtnClick(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses log, Velthuis.Bigdecimals, Velthuis.bigintegers;
// 有効桁数入力
function InPrecision(s: string): integer;
var
ch : integer;
begin
val(s, Result, ch);
if ch <> 0 then begin
application.MessageBox('有効桁数に間違いがあります。','注意',0);
result := -1;
exit;
end;
if Result < 1 then begin
application.MessageBox('有効桁数は1以上にしてください。','注意',0);
end;
if Result > 2500 then begin
application.MessageBox('有効桁数は2500迄にしてください。','注意',0);
result := -1;
end;
end;
// 指数の無い場合の数値確認
// x: 'e','E'のない数字文字列
// ca: 0 '.' がある場合 1 ない場合
// 問題が無い場合 0を返します
function numeralfloatcheck(x: string; ca: byte): integer;
var
len, dn, n, d : integer;
num, numb : string;
flg : boolean;
snum : integer;
begin
len := length(x); // 文字長さ
snum := 1;
num := x[1]; // 1文字目
dn := 0;
flg := true;
if num = '+' then inc(snum); // '+' パス
if num = '-' then inc(snum); // '-' パス
if num = '.' then begin // '.'
inc(dn); // '.'カウントインクリメント
inc(snum); // パス
end;
for n := snum to len do begin // snum からlen 迄数値確認
num := x[n];
if num = '.' then begin // '.'
inc(dn); // '.'カウントインクリメント
continue; // パス
end;
flg := false;
for d := 0 to 9 do begin // 0~9の値か確認
numb := inttostr(d);
if numb = num then begin
flg := true;
break;
end;
end;
if flg = false then break;
end;
if ca = 0 then begin // '.'あり条件だったら
if dn > 1 then flg := false; // '.'1個迄なら0k
end
else // '.'無条件だったら
if dn > 0 then flg := false; // '.'があったらMG
if flg then result := 0
else result := 1;
end;
// 入力確認
function incheck(s, m: string): boolean;
const
ec = 'e';
eo = 'E';
dt = '.';
var
fs, es : string;
ch, p, po, leng : integer;
begin
result := false;
p := pos(ec, s); // 'e' の位置
po := pos(eo, s); // 'E' の位置
p := p + po;
if p = 0 then begin // 'e' 'E' が無かったら
ch := numeralfloatcheck(s, 0); // '.'がある条件で確認無くても良い
if ch <> 0 then begin
application.MessageBox(' 入力値に間違いがあります。','注意',0);
exit;
end;
result := true;
exit;
end;
leng := length(s);
fs := '';
fs := copy(s, 1, p - 1); // 'e'の前の文字取り出し
es := '';
es := copy(s, p + 1, leng - p); // 'e'の後ろの文字取り出し
ch := numeralfloatcheck(fs, 0); // 'e'の前の文字の確認 '.'がある条件で確認無くても良い
if ch <> 0 then begin
application.MessageBox(' 入力値に間違いがあります。','注意',0);
exit;
end;
if es <> '' then begin // 'e'の後ろの文字確認
ch := numeralfloatcheck(es, 1); // '.'が無い条件で確認
if ch <> 0 then begin
application.MessageBox(' 入力値に間違いがあります。','注意',0);
exit;
end;
end;
result := true;
end;
procedure TForm1.CalcBtnClick(Sender: TObject);
const
MAXX = '1e500000';
MINX = '1e-500000';
var
x, y, mnx: bigdecimal;
Precision : integer;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
begin
if not incheck(XinEdit.Text, 'xの') then exit;
x := XinEdit.Text;
mnx := MAXX;
if x > mnx then begin
application.MessageBox(' 入力値が大きすぎます。','注意',0);
exit;
end;
mnx := MINX;
if x < mnx then begin
application.MessageBox(' 入力値が小さすぎます。','注意',0);
exit;
end;
Precision := InPrecision(PrecisionEdit.Text); // 有効桁数入力
if Precision < 1 then exit;
StopWatch := TStopwatch.StartNew;
BigDecimal.DefaultPrecision := Precision;
if checkbox1.Checked = false then
y := log_big(x, 0)
else
y := log_big(x, 1);
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
Edit1.text := '演算時間 = ' + intTostr(ElapsedMillseconds) + 'msec';
memo1.Lines.Append(y.ToPlainString);
end;
procedure TForm1.ClearBtnClick(Sender: TObject);
begin
Memo1.Clear;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
memo1.Clear;
end;
end.
![]() log_x.zip
log_x.zip
三角関数、逆三角関数、その他関数 に戻る