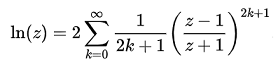
対数計算(複素数)
複素数の対数計算プログラムの検討をします。
複素数の対数計算は、プログラム開発ツールに組み込まれているので、必用無いのですが、複素数の対数計算は、複素数としての取扱いに特徴があるので取り上げてみました。
通常の計算はLog(x)の計算を参照して下さい。
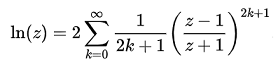
対数の計算は、上記式ですが、収束するためには、abs((z-1)/(z+1)) が1か1より小さくする必要があります。
zの値はZ>0であれば収束しますが、Zの値が1に近いほど高速に収束することになります。
実数の対数の場合は、負数の対数は計算できないのですが、複素数の場合は負数の計算が出来ます。
実数部が
負数の場合は、。実数部が正数になるように複素数の符号を反転して計算します。
その場合、:対数:の虚数部に π を加算又は減算して補正します。
計算上、実数の絶対値と、虚数の絶対値で大きい方の値を、新しい実数値とします。
虚数部と、実数部を入れ替えた場合は、:対数計算結果の虚数部に π/2 を加算又は減算して補正します。
zの値は1に近い方が速く収束するので、値が大きい場合は、10の値を除してじて、1より小さい場合は、乗じて1に近づけます。
除した回数、或いは乗じた回数分、対数変換後、10の対数を加算或いは減算します。
通常の計算Log(x)の計算では、2の値を使用しています。
複素数でのゼロの対数値は-∞です。
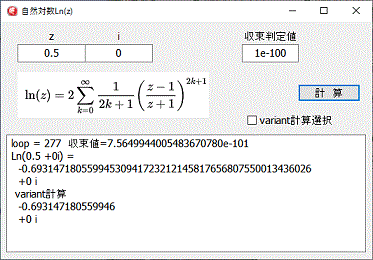 計算は、bigdecimal
とvariantによる複素数で計算しています。
計算は、bigdecimal
とvariantによる複素数で計算しています。
variantによる複素数計算は、確認の為で、前記計算式を使用しているわけではありません。
Delphiの中の複素数の計算を使用しています。
プログラム
プログラムには、BigDecimalが組み込んでありますが、組み込み方は第1種ケルビン関数v,x実数を参照して下さい。
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls,
Vcl.Imaging.pngimage;
type
TForm1 = class(TForm)
Memo1: TMemo;
zEdit: TLabeledEdit;
iEdit: TLabeledEdit;
epsEdit: TLabeledEdit;
Button1: TButton;
Image1: TImage;
CheckBox1: TCheckBox;
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses system.Math,System. VarCmplx, Velthuis.BigIntegers, Velthuis.Bigdecimals;
// 複素数構造体
type
CBig = record
r : bigdecimal;
i : bigdecimal;
end;
// CBig複素数の加算
function cadd(a, b: CBig): CBig;
begin
result.r := a.r + b.r;
result.i := a.i + b.i;
end;
// CBig複素数の減算
function csub(a, b: CBig): CBig;
begin
result.r := a.r - b.r;
result.i := a.i - b.i;
end;
// Cbig複素数の乗算
function cmul(a, b: Cbig): CBig;
begin
result.r := a.r * b.r - a.i * b.i;
result.i := a.r * b.i + a.i * b.r;
end;
// Cbig複素数の除算
function cdiv(a, b: Cbig): Cbig;
var
bb: Bigdecimal;
begin
bb := b.r * b.r + b.i * b.i;
if bb <> Bigdecimal.Zero then begin
result.r := (a.r * b.r + a.i * b.i) / bb;
result.i := (a.i * b.r - a.r * b.i) / bb;
end
else begin
result.r := Bigdecimal.Zero;
result.i := Bigdecimal.Zero;
end;
end;
// Cbigの絶対値
function cabs(a : cbig; dpcs : integer): bigdecimal;
var
arh2, aih2 : bigdecimal;
tmp : bigdecimal;
begin
arh2 := a.r * a.r;
aih2 := a.i * a.i;
tmp := arh2 + aih2;
result := bigdecimal.Sqrt(tmp, dpcs);
end;
// z 入力値 複素数
// eps 収束判定値
// dpcs 有効桁数
// ndis 収束表示 true 表示 false 非表示
function log_big_sub(z : Cbig; eps : bigdecimal; dpcs: integer; ndis: boolean): Cbig;
const
NN = 1000000;
var
s, x, zm1, zp1, xh2, xg, n2p1 : CBig;
one, two : Cbig;
xgsn : Cbig;
asabs, nabs : bigdecimal;
n : integer;
begin
one.r := Bigdecimal.One; // 1
one.r := one.r.RoundToPrecision(dpcs);
one.i := Bigdecimal.Zero; //
two := cadd(one, one); // 2
zm1 := csub(z, one); // z - 1
zp1 := cadd(z, one); // z + 1
x := cdiv(zm1, zp1); // x = (z-1)/(z+1)
s.r := Bigdecimal.Zero;
s.i := Bigdecimal.Zero;
xh2 := cmul(x, x); // x^2
xg := x; // n = 0; x^(2n+1)
n2p1 := one; // 2n+1 = 1
n := 0;
repeat
xg.r := xg.r.RoundToPrecision(dpcs);
xg.i := xg.i.RoundToPrecision(dpcs);
n2p1.r := n2p1.r.RoundToPrecision(dpcs);
n2p1.i := n2p1.i.RoundToPrecision(dpcs);
xgsn := cdiv(xg, n2p1); // x^(2n+1) / (2n+1)
s := cadd(s, xgsn); // Σ
xg := cmul(xg, xh2); // x^(2n+1)
n2p1 := cadd(n2p1, two); // 2n + 1
inc(n);
asabs := cabs(xgsn, dpcs);
until (asabs < eps) or (n > NN);
nabs := asabs.RoundToPrecision(20);
if n >= NN then form1.Memo1.Lines.Append('計算範囲内で収束しませんでした 答えは正しくない可能性があります。');
if ndis then form1.Memo1.Lines.Append('loop = ' + intTostr(n) + ' 収束値=' + nabs.ToString);
s := cmul(s, two);
result := s;
end;
// z 因数
// eps 収束判定値
// dpcs 有効桁数
// 返り値 対数複素数
function log_big(z : Cbig; eps : bigdecimal; dpcs: integer): Cbig;
const
pi_bigs = '3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117';
var
zb : Cbig;
z10, z10n : cbig;
Zmax, ten, one, bn : bigdecimal;
pi_big, pi_big2: bigdecimal;
begin
if (z.r = 0) and (z.i = 0) then begin
result.r := 0;
result.i := 0;
exit;
end;
bigdecimal.DefaultPrecision := dpcs;
pi_big := pi_bigs;
pi_big2 := pi_big / bigdecimal.Two;
zb := z;
// 虚数と実数両方ともゼロでないなら 実数部側を大きな値にして演算誤差を小さくします
if (zb.r <> bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin
if zb.i.Abs(zb.i) > zb.r.Abs(zb.r) then begin // 虚数の絶対値が実数の絶対値より大きい時入れ替え
z.r := zb.i;
z.i := zb.r;
if zb.i < bigdecimal.Zero then begin // 虚数が負数だったら符号反転
z.r := -z.r;
z.i := -z.i;
end;
end
else begin // 虚数の絶対値が実数の絶対値と等しいか小さい時
if zb.r < bigdecimal.Zero then begin // 実数の値が負数だったら符号反転
z.r := -zb.r;
z.i := -zb.i;
end;
end;
end;
// z.rが0でz.iがゼロでない時 虚数部と実数部入れ替え
if (zb.r = bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin
z.r := zb.i;
z.i := zb.r;
if z.r < bigdecimal.Zero then z.r := -z.r; // 実数部が負数だったら符号反転 虚数部ゼロなのでそのまま
end;
// 実数部が負数ので虚数部ゼロの時符号を反転 虚数部ゼロなのでそのまま
if (zb.r <> bigdecimal.Zero) and (zb.i = bigdecimal.Zero) then
if zb.r < bigdecimal.Zero then z.r := -zb.r;
// 10の対数を利用して大きな値の計算を速くします
ten := '10';
one := bigdecimal.One;
bn := bigdecimal.Zero;
z10.r := ten;
z10.i := bigdecimal.Zero;
z10 := log_big_sub(z10, eps, dpcs, false); // 10の対数
zmax := cabs(z, dpcs); // zの絶対値
// 10で除算又は乗算して値がの値が1~10の範囲に入るようにします。
repeat
if zmax > ten then begin // zmaxが10より大きい時10で除算
z.r := z.r / ten;
z.i := z.i / ten;
zmax := zmax / ten;
bn := bn + one; // 10で除算した回数 +になります。
end;
if zmax < one then begin // zmaxが1より小さい時10を乗算
z.r := z.r * ten;
z.i := z.i * ten;
zmax := zmax * ten;
bn := bn - one; // 10を乗算した回数 -になります。
end;
until (zmax <= ten) and (zmax >= one);
//----------------------------------------
// 修正された値で対数計算
result := log_big_sub(z, eps, dpcs, true);
// 10の対数補正
z10n.r := z10.r * bn; // 加算する対数値計算10の対数値のn倍
// z10n.i := z10.i * bn;
result.r := result.r + z10n.r; // 10の対数値のn倍加算
// result.i := result.i + z10n.i;
//----------------------------------------
// z.rがゼロでz.iがゼロでない時 虚数部π/2補正
if (zb.r = bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin
if zb.i >= bigdecimal.Zero then result.i := result.i + pi_big2
else result.i := result.i - pi_big2;
end;
// z.rの値が負数のきと符号を変更して計算しているの虚数部π補正。
if (zb.r < bigdecimal.Zero) and (zb.i = bigdecimal.Zero) then
result.i := result.i + pi_big;
// 虚数と実数両方ともゼロでない時
if (zb.r <> bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin
// 次数部絶対値より虚数部の絶対値が大きい場合
if zb.i.Abs(zb.i) > zb.r.Abs(zb.r) then begin
if zb.i > bigdecimal.Zero then result.i := -result.i + pi_big2 // π/2補正
else result.i := -result.i - pi_big2;
end
// 実数部が負数の時
else begin
if zb.r < bigdecimal.Zero then
if zb.i > bigdecimal.Zero then result.i := result.i + pi_big // π補正
else result.i := result.i - pi_big
end;
end;
end;
// variant double 計算
// Ln(z) = 2arctanh{(z-1)/z+1)} 対数計算
function lnd(dz, di : double): variant;
var
zi: variant;
c10, c10c : variant;
pc, mc : integer;
max : double;
argf : boolean;
begin
result := varascomplex(result);
c10 := varascomplex(c10);
c10c := varascomplex(c10c);
zi := varascomplex(zi);
c10.real := 10;
c10.Imaginary := 0;
c10c := 2 * VarComplexArcTanH((c10 - 1) / (c10 + 1)); // len(10+0i)
zi.real := dz;
zi.Imaginary := di;
max := VarComplexAbs(zi); // 絶対値
pc := 0;
mc := 0;
repeat
if max >= 10 then begin
max := max / 10;
zi.real := zi.real / 10;
zi.Imaginary := zi.Imaginary / 10;
inc(pc);
end;
if max < 1 then begin
max := max * 10;
zi.real := zi.real * 10;
zi.Imaginary := zi.Imaginary * 10;
inc(mc);
end;
until (max < 10) and (max >= 1);
// real < 0 の時 分母がゼロになり計算出来ない事があるので符号を反転します。
argf := false;
if zi.real < 0 then begin
zi.real := -zi.real;
zi.Imaginary := -zi.Imaginary;
argf := true;
end;
result := 2 * VarComplexArcTanH((zi - 1) / (zi + 1));
if pc > 0 then result.real := result.real + c10c * pc;
if mc > 0 then result.real := result.real - c10c * mc;
// real<0 の時符号を反転して計算しているので虚数部にπを加算して補正します。
if argf then result.Imaginary := result.Imaginary + pi;
end;
// 複素数の対数計算
// 50桁の精度の為 除算有効桁数100桁
procedure TForm1.Button1Click(Sender: TObject);
label
VA;
const
dpcs = 100; // 除算有効桁数
var
ch : integer;
zd, id, epsd : double;
z, ans : CBig;
eps : bigdecimal;
dans, xc : variant;
begin
val(zedit.Text, zd, ch);
if ch <> 0 then begin
application.MessageBox('zの値に間違いがあります。','注意',0);
exit;
end;
val(iedit.Text, id, ch);
if ch <> 0 then begin
application.MessageBox('iの値に間違いがあります。','注意',0);
exit;
end;
val(epsedit.Text, epsd, ch);
if ch <> 0 then begin
application.MessageBox('収束判定値に間違いがあります。','注意',0);
exit;
end;
if (epsd > 1e-1) then begin
application.MessageBox('収束判定値は。0.01より小さくし下さい。','注意',0);
exit;
end;
if (epsd <= 0) then begin
application.MessageBox('収束判定値は。0 あるいは、負数ではいけません。','注意',0);
exit;
end;
// 入力値をテキスト形式で読み込み多倍長数値に変換します、変換誤差防止です。
z.r := zedit.Text;
z.i := iedit.Text;
eps := epsedit.Text;
memo1.Clear;
application.ProcessMessages;
// 虚数と実数両方ともゼロの場合-∞
if (z.r = bigdecimal.Zero) and (z.i = bigdecimal.Zero) then begin
memo1.Lines.Append('loop = 0 演算出来ません。');
memo1.Lines.Append('Ln(0 + 0i) =');
memo1.Lines.Append(' -∞');
memo1.Lines.Append(' 0 i');
goto VA;
end;
// 対数計算
ans := log_big(z, eps ,dpcs);
// 計算結果表示
ans.r := ans.r.RoundToPrecision(50); // 50桁に丸め
ans.i := ans.i.RoundToPrecision(50);
if ans.r = bigdecimal.Zero then ans.r := '0';
if ans.i = bigdecimal.Zero then ans.i := '0';
if id >= 0 then
memo1.Lines.Append('Ln(' + floattostr(zd) + ' +' + floatTostr(id) + 'i) = ')
else
memo1.Lines.Append('Ln(' + floattostr(zd) + ' ' + floatTostr(id) + 'i) =');
memo1.Lines.Append(' ' + ans.r.ToString);
if ans.i >= bigdecimal.Zero then
memo1.Lines.Append(' +' + ans.i.ToString + ' i')
else
memo1.Lines.Append(' ' + ans.i.ToString + ' i');
VA:
// variant double 計算
xc := varascomplex(xc);
xc.real := zd;
xc.Imaginary := id;
if (zd <> 0) or (id <> 0) then begin
if checkbox1.Checked then begin
memo1.Lines.Append(' variant計算 Ln(z)');
dans := VarComplexLn(xc); // complexLn計算
end
else begin
memo1.Lines.Append(' variant計算 2*arctanh((z-1)/(z-1))');
// dans := VarComplexarctanh((xc * xc - 1)/(xc * xc + 1));
dans := lnd(zd, id); // 2arctanh{(z-1)/z+1)} 計算
end;
memo1.Lines.Append(' ' + floattostr(dans.real));
if dans.Imaginary >= 0 then
memo1.Lines.Append(' +' + floattostr(dans.Imaginary) + ' i')
else
memo1.Lines.Append(' ' + floattostr(dans.Imaginary) + ' i');
end
else begin
memo1.Lines.Append(' variant計算');
memo1.Lines.Append(' -∞');
memo1.Lines.Append(' 0 i');
end;
end;
end.
![]() log_function_big.zip
log_function_big.zip
三角関数、逆三角関数、その他関数 に戻る