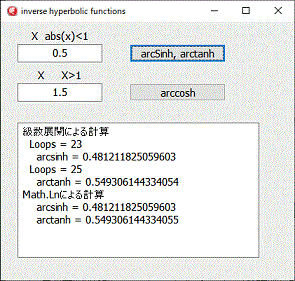
プログラムは、級数展開による方法と、自然対数による計算で作成されています。delphiでは arcsinh, arccosh, arctanhとなっていますが、ここでは arsinh, arcosh, artanh として作成しています。
級数展開の場合、arsinh に与える値は、1以下でないと計算できません、実際の値には制限がありません。
また、級数展開となっていますが、arcoshの計算には、自然対数の計算がはいります。
逆双曲線関数
逆双曲線関数(inverse hyperbolic functions)の詳細については、インターネットで検索してください。
逆双曲線関数の計算には、級数展開による方法と、自然対数を用いて計算する方法が有りますが、級数展開による方法は、計算できる値の大きさが制限されること、収束性が悪いので、自然対数を利用した方法をメインにします。
まず、級数展開による方法てプログラムを作成しました。
Delphiには、逆双曲線関数が標準で組み込まれているので参考プログラムです。
級数展開式は、ウィキペディア（Wikipedia）逆双曲線関数を参考にしてください。
プログラムは、級数展開による方法と、自然対数による計算で作成されています。
delphiでは arcsinh, arccosh, arctanhとなっていますが、ここでは arsinh, arcosh, artanh
として作成しています。
級数展開の場合、arsinh に与える値は、1以下でないと計算できません、実際の値には制限がありません。
また、級数展開となっていますが、arcoshの計算には、自然対数の計算がはいります。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
LabeledEdit1: TLabeledEdit;
BitBtn1: TBitBtn;
LabeledEdit2: TLabeledEdit;
BitBtn2: TBitBtn;
Memo1: TMemo;
procedure BitBtn1Click(Sender: TObject);
procedure BitBtn2Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses system.Math;
function arsinh(x : double): double;
var
i: integer;
ar, arb, f, v: double;
begin
i := 1;
v := - 1 / 2;
f := x * x * x;
ar := x + v * f / (i * 2 + 1);
repeat
inc(i);
arb := ar;
f := f * x * x;
v := - v * (i * 2 - 1) / (i * 2);
ar := ar + v * f / (i * 2 + 1);
until (arb = ar) or (i > 100000);
result := ar;
Form1.Memo1.Lines.Append(' Loops = ' + intTostr(i));
end;
function artanh(x : double): double;
var
i : integer;
ar, arb, f, v: double;
begin
v := 1;
f := x;
ar := x;
i := 1;
repeat
arb := ar;
f := f * x * x;
v := i * 2 + 1;
ar := ar + f / v;
inc(i);
until (arb = ar) or (i > 100000);
result := ar;
Form1.Memo1.Lines.Append(' Loops = ' + intTostr(i));
end;
function arcosh(x : double): double;
var
i : integer;
ar, arb, f, v: double;
begin
ar := ln(2 * x);
f := x * x;
v := 1 / 2;
i := 1;
ar := ar - v / f / (i * 2);
repeat
inc(i);
arb := ar;
f := f * x * x;
v := v * (i * 2 - 1) / (i * 2);
ar := ar - v / f / (i * 2);
until (arb = ar) or (i > 100000);
result := ar;
Form1.Memo1.Lines.Append(' Loops = ' + intTostr(i));
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
var
ch : integer;
x, ar : double;
begin
val(labelededit1.Text, x, ch);
if ch <> 0 then begin
application.MessageBox('入力値に間違いがあります。','注意',0);
exit;
end;
if abs(x) >= 1 then begin
application.MessageBox('Xの絶対値は１以下にして下さい。','注意',0);
exit;
end;
memo1.Clear;
memo1.Lines.Append('級数展開による計算');
ar := arsinh(x);
memo1.Lines.Append(' arcsinh = ' + floatTostr(ar));
ar := artanh(x);
memo1.Lines.Append(' arctanh = ' + floatTostr(ar));
memo1.Lines.Append('Math.Lnによる計算');
ar := ln(x + sqrt(x * x + 1));
memo1.Lines.Append(' arcsinh = ' + floatTostr(ar));
ar := ln((1 + x)/ (1 - x)) / 2;
memo1.Lines.Append(' arctanh = ' + floatTostr(ar));
end;
procedure TForm1.BitBtn2Click(Sender: TObject);
var
ch : integer;
x, ar : double;
begin
val(labelededit2.Text, x, ch);
if ch <> 0 then begin
application.MessageBox('入力値に間違いがあります。','注意',0);
exit;
end;
if abs(x) <= 1 then begin
application.MessageBox('Xの絶対値は１より大きくして下さい。','注意',0);
exit;
end;
memo1.Clear;
memo1.Lines.Append('級数展開による計算');
ar := arcosh(x);
memo1.Lines.Append(' arccosh = ' + floatTostr(ar));
memo1.Lines.Append('Math.Lnによる計算');
ar := ln(x + sqrt(x + 1) * sqrt(x - 1));
memo1.Lines.Append(' arccosh = ' + floatTostr(ar));
end;
end.
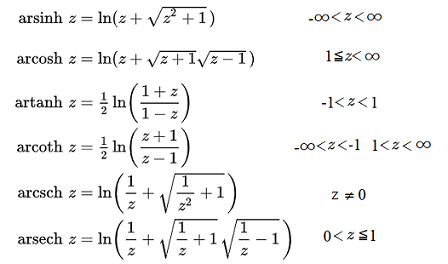左は、自然対数による逆双曲線関数です。
doubleでの精度の逆双曲線関数がdelphiには標準であるので、bigdecimalでのプログラムです。
Big_math.pasには、arsinh,
arcos, artanh が組み込んであります、arcsch, arsech, arcothは逆数を取ればよいので組み込んでありません。
biginteger,bigDecimalの組み込みはベルヌーイ数 その4を参照、
bigdecimalのlog founction(自然対数)に関してはLog functionを参照してください。
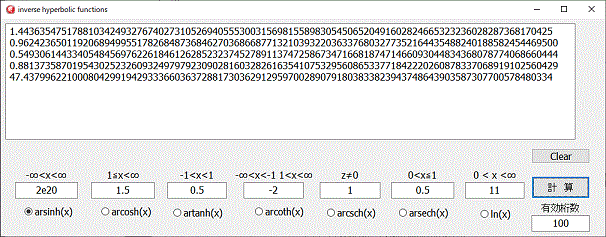各計算式を見ると、Z+1或いは、1/z+1が含まれています。
この場合、入力値と、有効桁数の関係で、桁落ちにより正しい答えがでない場合があるので注意が必要です。
大きな値 1.5e100000,
2e12000等
又はゼロに近い小さな値 3e-200000 等の値を入力された場合、この値に1を加算すると、値をあらわすのに、メモリーを大量に消費しますし、演算も非常に遅くなるので、指数部の値で入力制限をしています。
プログラム
main.pas
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
Memo1: TMemo;
LabeledEdit3: TLabeledEdit;
LabeledEdit4: TLabeledEdit;
LabeledEdit5: TLabeledEdit;
LabeledEdit6: TLabeledEdit;
RadioButton1: TRadioButton;
RadioButton2: TRadioButton;
RadioButton3: TRadioButton;
RadioButton4: TRadioButton;
RadioButton5: TRadioButton;
RadioButton6: TRadioButton;
CalcBtn: TBitBtn;
ClearBtn: TBitBtn;
pcsedit: TLabeledEdit;
LabeledEdit7: TLabeledEdit;
RadioButton7: TRadioButton;
procedure CalcBtnClick(Sender: TObject);
procedure ClearBtnClick(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses sub, Velthuis.Bigdecimals, Velthuis.bigintegers;
// 指数の無い場合の数値確認
// x: 'e','E'のない数字文字列
// ca: 0 '.' がある場合 1 ない場合
// 問題が無い場合 0を返します
function numeralfloatcheck(x: string; ca: byte): integer;
var
len, dn, n, d : integer;
num, numb : string;
flg : boolean;
snum : integer;
begin
len := length(x); // 文字長さ
snum := 1;
num := x[1]; // １文字目
dn := 0;
flg := true;
if num = '+' then inc(snum); // '+' パス
if num = '-' then inc(snum); // '-' パス
if num = '.' then begin // '.'
inc(dn); // '.'カウントインクリメント
inc(snum); // パス
end;
for n := snum to len do begin // snum からlen 迄数値確認
num := x[n];
if num = '.' then begin // '.'
inc(dn); // '.'カウントインクリメント
continue; // パス
end;
flg := false;
for d := 0 to 9 do begin // 0～9の値か確認
numb := inttostr(d);
if numb = num then begin
flg := true;
break;
end;
end;
if flg = false then break;
end;
if ca = 0 then begin // '.'あり条件だったら
if dn > 1 then flg := false; // '.'1個迄なら0k
end
else // '.'無条件だったら
if dn > 0 then flg := false; // '.'があったらMG
if flg then result := 0
else result := 1;
end;
// 入力確認
// m入力数字文字列
function incheck(s, m: string): boolean;
const
ec = 'e';
eo = 'E';
dt = '.';
var
fs, es : string;
ch, p, po, leng : integer;
begin
result := false;
p := pos(ec, s); // 'e' の位置
po := pos(eo, s); // 'E' の位置
p := p + po;
if p = 0 then begin // 'e' 'E' が無かったら
ch := numeralfloatcheck(s, 0); // '.'がある条件で確認無くても良い
if ch <> 0 then begin
application.MessageBox(' 入力値に間違いがあります。','注意',0);
exit;
end;
result := true;
exit;
end;
leng := length(s);
fs := '';
fs := copy(s, 1, p - 1); // 'e'の前の文字取り出し
es := '';
es := copy(s, p + 1, leng - p); // 'e'の後ろの文字取り出し
ch := numeralfloatcheck(fs, 0); // 'e'の前の文字の確認 '.'がある条件で確認無くても良い
if ch <> 0 then begin
application.MessageBox(' 入力値に間違いがあります。','注意',0);
exit;
end;
if es <> '' then begin // 'e'の後ろの文字確認
ch := numeralfloatcheck(es, 1); // '.'が無い条件で確認
if ch <> 0 then begin
application.MessageBox(' 入力値に間違いがあります。','注意',0);
exit;
end;
end;
result := true;
end;
// 有効桁数入力
function InPrecision(s: string): integer;
var
ch : integer;
begin
val(s, Result, ch);
if ch <> 0 then begin
application.MessageBox('有効桁数に間違いがあります。','注意',0);
result := -1;
exit;
end;
if Result < 1 then begin
application.MessageBox('有効桁数は１以上にしてください。','注意',0);
end;
if Result > 2500 then begin
application.MessageBox('有効桁数は2500迄にしてください。','注意',0);
result := -1;
end;
end;
// 指数値による値の値の大きさチェック
function emaxmincheck(z: bigdecimal): boolean;
var
k: integer;
begin
result := true;
k := echeck(z);
if k > 500000 then begin
application.MessageBox('値が大きすぎます。','incheck',0);
result := false;
end;
if k < -500000 then begin
application.MessageBox('値が小さすぎます。','incheck',0);
result := false;
end;
end;
// 計算
// ar***h(x)のxの値が有効桁数より大きくなると、ar***h(x)を求める対数計算の中の
// x+1又はx-1の計算が桁落ちにより正しい結果が得られません。
procedure TForm1.CalcBtnClick(Sender: TObject);
label
EXT;
const
MS = '入力値の値がが有効桁数に対して大きいので正しい結果が得られ無い場合があります。';
var
pcs, pcsback, epcs: integer;
z, ans: bigdecimal;
begin
pcs := InPrecision(pcsedit.Text);
if pcs < 1 then exit;
pcsBack := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ
BigDecimal.DefaultPrecision := pcs;
ans := '0';
if radiobutton1.Checked = true then begin
if not incheck(labelededit1.text, 'arsinh') then goto EXT;
z := labelededit1.text;
if not emaxmincheck(z) then goto EXT; // 指数部の値チェック
epcs := echeck(z); // 指数部取り出し
if epcs > pcs then memo1.Lines.Append(MS); // 入力指数値が有効桁数より大きかったら
ans := arsinh_big(z);
end;
if radiobutton2.Checked = true then begin
if not incheck(labelededit2.text, 'arcosh') then goto EXT;
z := labelededit2.text;
if not emaxmincheck(z) then goto EXT; // 指数部の値チェック
epcs := echeck(z); // 指数部取り出し
if epcs > pcs then memo1.Lines.Append(MS); // 入力指数値が有効桁数より大きかったら
ans := arcosh_big(z);
end;
if radiobutton3.Checked = true then begin
if not incheck(labelededit3.text, 'artanh') then goto EXT;
z := labelededit3.text;
if not emaxmincheck(z) then goto EXT; // 指数部の値チェック
ans := artanh_big(z);
end;
if radiobutton4.Checked = true then begin
if not incheck(labelededit4.text, 'arcoth') then goto EXT;
z := labelededit4.text;
if not emaxmincheck(z) then goto EXT; // 指数部の値チェック
epcs := echeck(z); // 指数部取り出し
if epcs > pcs then memo1.Lines.Append(MS); // 入力指数値が有効桁数より大きかったら
ans := arcoth_big(z);
end;
if radiobutton5.Checked = true then begin
if not incheck(labelededit5.text, 'arcsch') then goto EXT;
z := labelededit5.text;
if not emaxmincheck(z) then goto EXT; // 指数部の値チェック
epcs:= echeck(z); // 指数部取り出し
if epcs > pcs then memo1.Lines.Append(MS); // 入力指数値が有効桁数より大きかったら
ans := arcsch_big(z);
end;
if radiobutton6.Checked = true then begin
if not incheck(labelededit6.text, 'arsech') then goto EXT;
z := labelededit6.text;
if not emaxmincheck(z) then goto EXT; // 指数部の値チェック
ans := arsech_big(z);
end;
if radiobutton7.Checked = true then begin
if not incheck(labelededit7.text, 'ln') then goto EXT;
z := labelededit7.text;
if not emaxmincheck(z) then goto EXT; // 指数部の値チェック
ans := log_big(z);
end;
memo1.Lines.append(ans.tostring);
EXT:
BigDecimal.DefaultPrecision := pcsBack; // 除算演算精度復帰
end;
procedure TForm1.ClearBtnClick(Sender: TObject);
begin
memo1.Clear;
end;
end.
sub.pas
// 有効桁数が1000桁程度迄でそれを超えると、演算が非常に遅くなります。 // 有効桁数100桁程度であれば問題ありません。 // 2500桁位が上限です、それ以上必要な場合は収束ループの上限設定を外して下さい。 // 64ビットでコンパイルしないと演算が遅くなります。 unit sub; interface uses Velthuis.Bigdecimals, System.SysUtils, Vcl.Forms, Velthuis.BigIntegers; //uses Velthuis.Bigdecimals, System.SysUtils, Vcl.Forms, Velthuis.BigIntegers, main; function log_big(x: bigdecimal): bigdecimal; function arsinh_big(x: bigdecimal): bigdecimal; function arcosh_big(x: bigdecimal): bigdecimal; function artanh_big(x: bigdecimal): bigdecimal; function arcoth_big(x: bigdecimal): bigdecimal; function arcsch_big(x: bigdecimal): bigdecimal; function arsech_big(x: bigdecimal): bigdecimal; function echeck(z: bigdecimal): integer; implementation // 数字文字列のeの後の数値を返します function echeck(z: bigdecimal): integer; const ec = 'e'; eo = 'E'; var p, po, leng : integer; estr, s : string; begin s := z.ToString; // bigdecimal -> text 指数表示; p := pos(ec, s); // 'e' の位置 po := pos(eo, s); // 'E' の位置 p := p + po; if p = 0 then begin // 'e' 'E' が無かったら result := 0; exit; end; leng := length(s); estr := copy(s, p + 1, leng - p); // 'e'の後ろの文字取り出し result := strToint(estr) // text->数値 end; // 小さい値のlog計算 // xi 実数 // dpcs 有効桁数 // ans log値 // 戻り値 Loopオーバーフロー 無し true 有り false // loop制限の無い場合 1e-4～1e4 が計算出来る範囲 // loop制限 5.8e-3 ～1.73e2 (kk=10000の場合) function Log_11(x: bigdecimal; dpcs: integer; var ans: bigdecimal): boolean; const KK = 10000; var one, two, x1, x2, i, s, last: bigdecimal; k : integer; begin result := true; one := '1'; two := '2'; x1 := (x - one) / (x + one); // x1 = (x-1)/(x+1) x2 := x1 * x1; // x1^2 x2 := x2.RoundToPrecision(dpcs); i := one; // i=1 s := x1; // s初期値 k := 0; // 長ループ脱出用カウンタ0 repeat x1 := x1 * x2; // x1^2n+1 x1 := x1.RoundToPrecision(dpcs); i := i + two; // 2n+1 last := s; // 判定用sの値保存 s := s + x1 / i; // Σs = s + x1^2n+1 / (2n+1) s := s.RoundToPrecision(dpcs); // 収束判定の為指定有効桁数以下丸め inc(k); // ループカウンタインクリメント until (last = s) or (k > KK); // 収束判定 ans := two * s; if k > kk then result := false; // Form1.Memo1.Lines.Append(intTostr(k)); end; // x = m * 2^n のnの値と2^nの値を戻します // result = n // ta = 2^n // m = x / 2^n function frexpa(x: bigdecimal; var ta: biginteger): integer; var tb: biginteger; xi, one: bigdecimal; n, j, s, pcs : integer; begin pcs := BigDecimal.DefaultPrecision; one := '1'; one := one.RoundToPrecision(pcs); xi := x; // x保存 if xi < one then x := one / x; // 1より小さかったら逆数 ta := '1'; n := 0; j := 0; // シフト回数クリア ta := '1'; // ta初期値 s := 4096; // s=4^i i = 6 repeat while x > ta do begin biginteger.ShiftLeft(ta, s, tb); // s分左シフト ta := tb; inc(j); // シフト回数インクリメント end; if (s > 1) and (j > 0) then begin // ta > x になったら dec(j); // シフト回数デクリメント biginteger.Shiftright(ta, s, tb); // s分右シフト ta := tb; end; n := n + s * j; // 2^nのn計算 j := 0; // シフト回数クリア s := s shr 2; // sの値を1/4にする 右へ2ビットシフト // s := s div 4; // sの値を1/4にする until s = 0; // s= ...16, 4, 1, 0 if xi < one then begin // より小さかったら n := -n + 1; // 2^nのn値負数 biginteger.Shiftright(ta, 1, tb); // 上式+1により右シフト ta := tb; end; result := n // ta = 2^n end; // loge(x) ln(x) // 級数展開 // 1e±500000 程度が限度 // sm<x<lastの範囲はlog_11(x)で計算 sm=0.01 last=50 // sm <xi< last の範囲外の場合 (0.7～xi～1.4) * 2^nに変換 xiが1に近いほど変換早い function log_bigf(xi: bigdecimal): bigdecimal; label EXT; const KK = 10000; var LOG2, SQRT2, two, last, s, sm, one, one1, k2, a: bigdecimal; k : integer; kb, ta : biginteger; dpcs : integer; begin dpcs := BigDecimal.DefaultPrecision; xi := xi.RoundToPrecision(dpcs); result := '0'; one1 := '1e500000'; if xi < one then begin last := one / xi; if last > one1 then begin application.MessageBox('値が小さすぎます。','log_big',0); exit; end; end; if xi > one1 then begin application.MessageBox('値が大きすぎます。','log_big',0); exit; end; if xi <= result then begin application.MessageBox('無効な値です。','log_big',0); exit; end; sm := '1e-2'; last := '5e1'; one := '1'; if xi = one then begin // result := '0'; // 設定済み goto EXT; end; if (xi > sm) and (xi < last) then begin // 指数の値が小さい場合はRC又はlog11計算 Log_11(xi, dpcs, a); // log11 result := a; goto EXT; end; two := '2'; Log_11(two, dpcs, LOG2); // log(2) SQRT2 := bigdecimal.Sqrt(two, dpcs * 2); // √2 k := frexpa(xi / SQRT2, ta); // x / √2 = m * 2^k ta = 2^k kb := k; // integer -> biginteger k2 := ta; // biginteger -> bigdecimal k2 := k2.RoundToPrecision(dpcs); if k < 0 then begin // kが負数だったら xi := xi * k2; xi := xi.RoundToPrecision(dpcs); // x * 2^k x=0.707～1.414 √2 end else begin // kが正数だったら xi := xi / k2; // x / 2^k x=0.707～1.414 √2 end; if xi <> one then // xi <> 1 なら Log_11(xi, dpcs, s) // log(xi) else s := '0'; // xi=1なら s=0 result := LOG2 * kb + s; // Form1.Memo1.Lines.Append(s.ToPlainString); EXT: result := result.RoundToPrecision(dpcs); end; // arsinh // arsinh(x)= ln(x+√(x^2+1)) // -∞<x<∞ function arsinh_big(x: bigdecimal): bigdecimal; var xx, one: bigdecimal; pcsback, dpcs : integer; rmback : BigDecimal.RoundingMode; begin pcsback := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ dpcs := pcsback + 5; // 指定精度 + α BigDecimal.DefaultPrecision := dpcs; BigDecimal.DefaultRoundingMode := rmNearesteven; if x <> 0 then begin one := '1'; xx := BigDecimal.Sqrt(x * x + one, dpcs * 2) + x; result := log_bigf(xx); result := result.RoundToPrecision(pcsback); end else result := '0'; BigDecimal.DefaultPrecision := pcsBack; // 除算演算精度復帰 BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰 end; // arcosh // arcosh(x)=ln(x+√(x+1)*√(x-1)) // 1≦x<∞ function arcosh_big(x: bigdecimal): bigdecimal; var xx, xp, xm, one: bigdecimal; pcsback, dpcs : integer; rmback : BigDecimal.RoundingMode; begin pcsback := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ dpcs := pcsback + 5; // 指定精度 + α one := '1'; if x < one then begin application.MessageBox('値が範囲外です。', 'arcosh_big', 0); result := 0; exit; end; BigDecimal.DefaultPrecision := dpcs; BigDecimal.DefaultRoundingMode := rmNearesteven; if x > one then begin xp := BigDecimal.Sqrt(x + one, dpcs * 2); xm := BigDecimal.Sqrt(x - one, dpcs * 2); xx := x + xp * xm; result := log_bigf(xx); result := result.RoundToPrecision(pcsback); end else result := '0'; BigDecimal.DefaultPrecision := pcsBack; // 除算演算精度復帰 BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰 end; // artanh // artanh(x)=1/2*ln((1+x)/(1-x)) // -1<x<1 function artanh_big(x: bigdecimal): bigdecimal; var xx, xp, xm, one, two, zero: bigdecimal; pcsback, dpcs : integer; rmback : BigDecimal.RoundingMode; begin pcsback := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ dpcs := pcsback + 5; // 指定精度 + α one := '1'; if BigDecimal.Abs(x) >= one then begin application.MessageBox('値が範囲外です。', 'artanh_big', 0); result := 0; exit; end; zero := '0'; if x = zero then begin result := '0'; exit; end; BigDecimal.DefaultPrecision := dpcs; BigDecimal.DefaultRoundingMode := rmNearesteven; xp := one + x; xm := one - x; xx := xp / xm; two := '2'; result := log_bigf(xx) / two; result := result.RoundToPrecision(pcsback); BigDecimal.DefaultPrecision := pcsBack; // 除算演算精度復帰 BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰 end; // arcoth // arcoth(x)=1/2*ln((x+1)/(x-1)) // -∞<x<-1 or 1<x<∞ function arcoth_big(x: bigdecimal): bigdecimal; var xx, xp, xm, one, two: bigdecimal; pcsback, dpcs : integer; rmback : BigDecimal.RoundingMode; begin pcsback := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ dpcs := pcsback + 5; // 指定精度 + α BigDecimal.DefaultPrecision := dpcs; BigDecimal.DefaultRoundingMode := rmNearesteven; one := '1'; if BigDecimal.Abs(x) <= one then begin application.MessageBox('値が範囲外です。', 'arcoth_big', 0); result := 0; exit; end; xp := x + one; xm := x - one; xx := xp / xm; two := '2'; result := log_bigf(xx) / two; result := result.RoundToPrecision(pcsback); BigDecimal.DefaultPrecision := pcsBack; // 除算演算精度復帰 BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰 end; // arcsch // arcsch(x)=ln(1/x+√(1/x^2+1)) // z≠0 function arcsch_big(x: bigdecimal): bigdecimal; var xx, xp, xm, one, zero: bigdecimal; pcsback, dpcs : integer; rmback : BigDecimal.RoundingMode; begin pcsback := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ dpcs := pcsback + 5; // 指定精度 + α BigDecimal.DefaultPrecision := dpcs; BigDecimal.DefaultRoundingMode := rmNearesteven; zero := '0'; one := '1'; if x = zero then begin application.MessageBox('値が範囲外です。', 'arcsch_big', 0); result := 0; exit; end; xp := one / (x * x) + one; xp := xp.RoundToPrecision(dpcs); xp := bigdecimal.Sqrt(xp, dpcs * 2); xm := one / x; xx := xm + xp; result := log_bigf(xx); result := result.RoundToPrecision(pcsback); BigDecimal.DefaultPrecision := pcsBack; // 除算演算精度復帰 BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰 end; // arsech // arsech(x)=ln(1/x+√(1/x+1)*√(1/x-1)) // 0<x≦1 function arsech_big(x: bigdecimal): bigdecimal; var xx, xp, xm, one, zero: bigdecimal; pcsback, dpcs : integer; rmback : BigDecimal.RoundingMode; begin pcsback := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ dpcs := pcsback + 5; // 指定精度 + α BigDecimal.DefaultPrecision := dpcs; BigDecimal.DefaultRoundingMode := rmNearesteven; zero := '0'; one := '1'; if (x < zero) or (x > one) then begin application.MessageBox('値が範囲外です。', 'arsech_big', 0); result := 0; exit; end; xp := one / x + one; xp := xp.RoundToPrecision(dpcs); xp := bigdecimal.Sqrt(xp, dpcs * 2); xm := one / x - one; xm := xm.RoundToPrecision(dpcs); xm := bigdecimal.Sqrt(xm, dpcs * 2); xx := one / x + xm * xp; result := log_bigf(xx); result := result.RoundToPrecision(pcsback); BigDecimal.DefaultPrecision := pcsBack; // 除算演算精度復帰 BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰 end; function log_big(x: bigdecimal): bigdecimal; var pcsback, dpcs : integer; rmback : BigDecimal.RoundingMode; begin pcsback := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ dpcs := pcsback + 5; // 指定精度 + α BigDecimal.DefaultPrecision := dpcs; BigDecimal.DefaultRoundingMode := rmNearesteven; result := log_bigf(x); result := result.RoundToPrecision(pcsback); BigDecimal.DefaultPrecision := pcsBack; // 除算演算精度復帰 BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰 end; end.
inverse_hyperbolic_function.zip
三角関数、逆三角関数、その他関数 に戻る