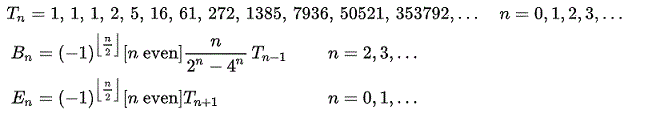
ベルヌーイ数 ５
オイラー数で、二項係数を使用しない、アルゴリズムSeidel's algorithm for Tnによるプログラムを作成したので、ベルヌーイ数でも作成しました。
Seidel's algorithm for Tn で
次のようになってます。
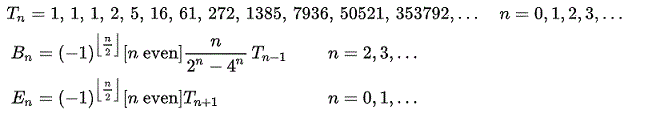
１
-> １ １
２ ２ １ <-
-> ２ ４ ５ ５
１６ １６ １４ １０ ５ <-
実際にプログラムを組む場合を考えてみます。
ベルヌーイ数用の値は、
上記数列の左側の値で、符号が無いと同時に、追加の計算が必要です。
符号については、Noが４おきなので、後から簡単に設定ができます。
ベルヌーイ数の係数を計算するのに、オイラー数のものをそのまま利用しても良いのですが、出来る限りシンプルにしたいので、ベルヌーイ数用の計算手順にします。
ベルヌーイ数
[0] [1] [2] [3] [4] [5] [6]
1 [0]=1 初期設定
2 1 1 -> {[1]=[0]+[1]} upから開始 up前値表示
2 2 1 <- [2]=[1] {[1]=[2]+[0]} [0]=[1]
4 2 4 5 5 -> {[1]=[0]+[1] [2]=[1]+[2] [3]=[2]+[3]}
16 16 14 10 5 <- [4]=[3] {[3]=[4]+[2] [2]=[3]+[1] [1]=[2]+[0]} [0]=[1]
6 16 32 46 56 61 61 -> {[1]=[0]+[1] [2]=[1]+[2] [3]=[2]+[3] [4]=[3]+[4] [5]=[4]+[5]}
272 272 256 224 178 122 61 <- [6]=[5] {[5]=[6]+[4] [4]=[5]+[3] [3]=[4]+[2] [2]=[3]+[1] [1]=[2]+[0]} [0]=[1]
(8) 272 Tnループ終了後
配列メモリーの[0]にBnの:係数値が出る様にして、計算手順の表を作成しました。
矢印 -> <-
ワンセットforで実行され更にその中の { } 内が更にforで実行する部分となります。
最初の0, 1は、Tn計算のループから外れる為、別途先に:計算:します。
まずは、分かりやすいようにCで作成しました。
オイラー数と違って、係数からベルヌーイ数に変換するルーチンが増えています。
分数表示の為のルーチンも増えているのでオイラー数よりは演算に時間がかかります。
下記のプログラムはDos窓で実行されます。
/*********************************************************** bernoulli number.c -- Bernoulli (ベルヌーイ) 数 ***********************************************************/ #include <stdio.h> #include <stdlib.h> /* 最大公約数 */ long long gcd(long long x, long long y) { long long t; while (y != 0) { t = x % y; x = y; y = t; } return x; } /* Tn Bn 変換 表示*/ int TnToBn(int n, long long tn, long long q) { long long b1, b2, g; char s[5] = " = \0"; b1 = n * tn; /* 分子 */ b2 = q * (q - 1); /* 分母 */ g = gcd(b1, b2); /* 最大公約数 */ b1 /= g; b2 /= g; if (n % 4 == 0) { /* 符号設定 */ b1 *= -1; s[3] = '\0'; } else s[3] = ' '; printf(" B(%2d)%s%lld / %lld\n", n, s, b1, b2); return 0; } #define N 22 /* 偶数指定 */ int main() { int j, n; long long b1, b2; static long long t[N - 1]; long long q; /* B0 */ n = 0; b1 = 1; b2 = 1; printf(" B(%2d) = %lld / %lld\n", n, b1, b2); /* B1 */ n = 1; b1 = -1; b2 = 2; printf(" B(%2d) = %lld / %lld\n", n, b1, b2); /* B2～ */ q = 1; /* 分母係数初期値 */ t[0] = 1; /* 分子係数初期値 */ /* Seidel's algorithm for Tn */ for (n = 2; n < N ; n += 2) { q = q << 2; /* 分母係数 q = q * 4 */ TnToBn(n, t[0], q); /* Bn値表示 */ for (j = 0; j <= n - 2; j++) t[j + 1] += t[j]; /* 分子係数計算 */ t[n] = t[n - 1]; for (j = n - 2; j >= 0; j--) t[j + 1] = t[j] + t[j + 2]; t[0] = t[1]; } /* 最後のBn値表示 */ q = q << 2; /* 分母係数 q = q * 4 */ TnToBn(N, t[0], q); printf("\n Enterキーを押して下さい"); getchar(); return EXIT_SUCCESS; }
プログラム
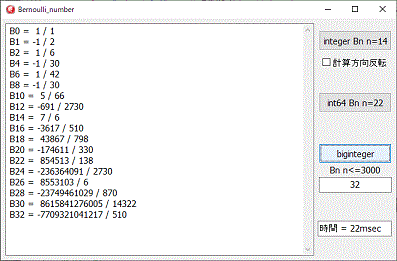integerのプログラムは、オイラーの計算手順を利用してベルヌーイ数を計算するプログラムを実行するものです参考で作成しました。
int64は、Bigintegerの前に作成したもので、計算手順の検証用に作成しものです、Bigintegerでの計算はInt64から僅かの変更で作成できるのて無くても作成にそれ程手間取りません。
未だ、Bigintegerに慣れていないので、取りあえず作成しました。
Bigintegerでの計算結果の検証用にも使用しています。
プログラムには、Bigintegerを使用します。
BigDecimalでも、問題なく計算できますが、整数しか取り扱わないので、BigIntegerにしています。
bigintegerの組み込みについては、ベルヌーイ数 その４を参照してください。
B2000を0.45sec(cpu依存)となり、今までのベルヌーイ数計算では一番早く計算できます。
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, system.Diagnostics,
Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Memo1: TMemo;
BitBtn1: TBitBtn;
Edit1: TEdit;
BitBtn2: TBitBtn;
LabeledEdit1: TLabeledEdit;
BitBtn3: TBitBtn;
CheckBox1: TCheckBox;
procedure BitBtn1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure BitBtn2Click(Sender: TObject);
procedure BitBtn3Click(Sender: TObject);
private
{ Private 宣言 }
function Ninput(var n: integer): boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
{
ベルヌーイ数計算アルゴリズム
B0,B1 個別表示
B2以降Seidel's algorithm 使用の計算手順です。
ベルヌーイ数計算時、最も無駄のない計算手順です。
Seidel's algorithm for Tn Bn用 B2～
0 1 2 3 4 5 6 7(8) Tn-1 n= 2,4,6,(8) 最後の表示は.ループ終了後
Tn = 1,1,1,2,5,16,61,272
[0] [1] [2] [3] [4] [5] [6] () forループ
1 [0]=1 初期値
2 1 1 -> ([1]=[0]+[1]) up方向計算 値t[0]表示
2 2 1 <- [2]=[1] ([1]=[2]+[0]) [0]=[1] down方向計算
4 2 4 5 5 -> ([1]=[0]+[1] ～ [3]=[2]+[3])
16 16 14 10 5 <- [4]=[3] ([3]=[4]+[2] ～ [1]=[2]+[0]) [0]=[1]
6 16 32 46 56 61 61 -> ([1]=[0]+[1] ～ [5]=[4]+[5])
272 272 256 224 178 122 61 <- [6]=[5] ([5]=[6]+[4] ～ [1]=[2]+[0]) [0]=[1]
8 Tn計算ループ終了後t[0]表示
}
uses Velthuis.BigIntegers;
const
Ni = 3000; // 最大ベルヌーイ数No Biginteger
// 最大公約数 ユークリッドの互除法 int64
function gcd_int64(x, y: int64): int64;
var
t : int64;
begin
while y <> 0 do begin
t := x mod y;
x := y;
y := t;
end;
result := x;
end;
//------------------------------------------------------------------------------
// ベルヌーイ数計算 integer n=14
// 参考プログラム
// 上のアルゴリズム表とは違います、オイラー数計算と同じ手順になっています。
// B0,B1は単独計算
// B2以降はSeidel's algorithmによる計算
// 配列のt[0]がベルヌーイ数用Tn B2～の値となりt[i]がオイラー数E2～となり、
// オイラー数用の配列利用はt[i]がベルヌーイ数用Tn B2～の値となりt[0]がオイラー数E2～となります。
// 最大のベルヌーイNo計算時のdown方向計算が無駄な計算となるのでif文で避けています。
// Seidel's algorithm for Tn B2～ Euler_numbersとの計算比較
procedure TForm1.BitBtn3Click(Sender: TObject);
const
k = 14; // k = 14より大きい値は1ntegwr オーバーフロー
var
t : array of integer;
i, j, m, n : integer;
b1, b2, q, g : integer;
B : integer;
kv2m1 : integer;
bstr : string;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
// 値表示
procedure memoout;
begin
if b1 < 0 then bstr := ' = '
else bstr := ' = ';
memo1.Lines.Append('B' + intTostr(n) + bstr + inttostr(b1) +' / ' + intTostr(b2));
end;
begin
StopWatch := TStopwatch.StartNew;
if checkbox1.checked = False then // ベルヌーイ数用
setlength(t, k) // 配列確保 値クリア
else // オイラー数と同じ
setlength(t, k + 1); // 配列確保 値クリア
b := 0; // b初期化 本来不要
memo1.Clear;
n := 0; b1 := 1; b2 := 1; memoout; // B0
n := 1; b1 := -1; b2 := 2; memoout; // B1
// Seidel's algorithm for Tn (オイラー数と同じループの場合 Tn値の取り出しが違います)
if checkbox1.checked = False then
t[1] := 1 // 分子初期値 ベルヌーイ数用ループ
else
t[0] := 1; // 分子初期値 オイラー数と同じループ
q := 1; // 分母初期値
kv2m1 := k div 2 - 1; // B0,B1が無いの -1
for m := 0 to kv2m1 do begin // for i = 0 step 2 B2～
i := m shl 1; // i = m * 2
// ベルヌーイ数用ループ
if checkbox1.checked = False then begin
for j := i downto 1 do t[j] := t[j + 1] + t[j - 1]; // <- 最初i=0時は実行無し
t[0] := t[1]; // Tn=t[0] ベルヌーイ数Tn
if m < kv2m1 then begin // 最後は実行しない
for j := 1 to i do t[j] := t[j] + t[j - 1] ; // -> 最初i=0時は実行無し
t[i + 1] := t[i]; // t[i] オイラー数
end;
end
// オイラー数と同じループ
else begin
for j := 1 to i do t[j] := t[j] + t[j - 1]; // ->
b := t[i]; // Tn = t[i] ベルヌーイ数Tn
if m < kv2m1 then begin // 最後は実行しない オイラー数では実行
t[i + 1] := t[i];
for j := i downto 1 do t[j] := t[j + 1] + t[j - 1]; // <-
t[0] := t[1]; // t[0] がオイラー数となります
end;
end;
n := i + 2; // ベルヌーイNo i + 2
// 分子の計算
if checkbox1.checked = False then // ベルヌーイ数用ループ用
b1 := n * t[0] // 分子 n * t[0] t[0]=Tn
else // オイラー数と同じループの場合
b1 := n * b; // 分子 n * b b=Tn
// 分母の計算
q := q shl 2; // 分母 2^n q = q * 4
b2 := q * (q - 1); // 〃 4^n - 2^n
// 最大公約数で分子分母を最小整数値に
g := gcd_int64(b1, b2); // 最大公約数
b1 := b1 div g;
b2 := b2 div g;
if n mod 4 = 0 then b1 := - b1; // 符号設定
memoout; // 値表示
end;
StopWatch.Stop;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
Edit1.text := '時間 = ' + intTostr(ElapsedMillseconds) + 'msec';
end;
//------------------------------------------------------------------------------
// 一番上のアルゴリズム説明によるプログラム
// ベルヌーイ数計算 int64 n=22
// B0,1を単独でけいさん、Bn n=2～k-1は up, n=k は最終downループ後
// Seidel's algorithm for Tn B2～
procedure TForm1.BitBtn1Click(Sender: TObject);
const
k = 22; // k = 22より大きい値は1nt64 オーバーフロー
var
t : array of int64;
j, n : integer;
b1, b2, q, g : int64;
bstr : string;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
// ベルヌーイ値表示
procedure memoout;
begin
if b1 < 0 then bstr := ' = '
else bstr := ' = ';
memo1.Lines.Append('B' + intTostr(n) + bstr + inttostr(b1) +' / ' + intTostr(b2));
end;
// Tnの値をBn値に変換表示
procedure TntoBn;
begin
b1 := n * t[0]; // 分子 n * Tn
q := q shl 2; // 分母 2^n q = q * 4
b2 := q * (q - 1); // 〃 4^n - 2^n
g := gcd_int64(b1, b2); // 最大公約数
b1 := b1 div g;
b2 := b2 div g;
if n mod 4 = 0 then b1 := - b1; // 符号設定
memoout; // 値表示
end;
begin
StopWatch := TStopwatch.StartNew;
memo1.Clear;
n := 0; b1 := 1; b2 := 1; memoout; // B0
n := 1; b1 := -1; b2 := 2; memoout; // B1
// Seidel's algorithm for Tn Bn値をt[0]としたベルヌーイ計算ループ B2～
setlength(t, k - 1); // 配列確保 値クリア
t[0] := 1; // 分子係数初期値
q := 1; // 分母係数初期値
n := 2; // forto n=2 初期値
repeat
TntoBn; // ベルヌーイ数表示Tn = t[0]
for j := 0 to n - 2 do t[j + 1] := t[j] + t[j + 1]; // ->
t[n] := t[n - 1];
for j := n - 2 downto 0 do t[j + 1] := t[j] + t[j + 2]; // <-
t[0] := t[1];
inc(n, 2); // forto n=n+2 step2
until n >= k;
TntoBn; // ベルヌーイ数表示Tn = t[0]
StopWatch.Stop;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
Edit1.text := '時間 = ' + intTostr(ElapsedMillseconds) + 'msec';
end;
//================================ Biginteger ==================================
// ベルヌーイNo入力処理
function TForm1.Ninput(var n: integer): boolean;
var
c : integer;
begin
result := true;
val(labelededit1.Text, n, c);
if c <> 0 then begin
memo1.Text := 'ベルヌーイNo に間違いがあります。';
result := false;
exit;
end;
if n < 0 then begin
memo1.Text := 'ベルヌーイNoはゼロ以上にして下さい。';
result := false;
end;
if n > NI then begin
memo1.Text := 'ベルヌーイNo が大きすぎます' + intTostr(NI) + '迄です。';
result := false;
end;
end;
// 最大公約数 ユークリッドの互除法 biginteger
function gcd_big(x, y: biginteger): biginteger;
var
t : biginteger;
begin
while y <> 0 do begin
t := x mod y;
x := y;
y := t;
end;
result := x;
end;
// ベルヌーイ数計算 biginteger
// B0,1を単独でけいさん、Bn n=2～k-1は up前, n=k はdownループ後
procedure TForm1.BitBtn2Click(Sender: TObject);
const
MM = 36; // ベルヌーイ数一覧表示範囲
var
t : array of biginteger;
j, n, k : integer;
b1, b2, q, g : biginteger;
bstr : string;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
// ベルヌーイ値表示
procedure memoout;
begin
if b1 < 0 then bstr := ' = '
else bstr := ' = ';
memo1.Lines.Append('B' + intTostr(n) + bstr + b1.ToString +' / ' + b2.ToString);
end;
// Tnの値をBn値に変換表示
procedure TntoBn;
begin
q := q shl 2; // 分母 2^n q = q * 4
if (k <= MM) or ((n > MM) and (n = k)) then begin
b1 := n * t[0]; // 分子 n * Tn
b2 := q * (q - 1); // 分母 4^n - 2^n
g := gcd_big(b1, b2); // 最大公約数
b1 := b1 div g;
b2 := b2 div g;
if n mod 4 = 0 then b1 := - b1; // 符号設定
memoout;
end; // 値表示
end;
begin
if not Ninput(k) then exit; // 計算ベルヌーイNo入力
StopWatch := TStopwatch.StartNew;
memo1.Clear;
if k <= MM then begin
n := 0; b1 := 1; b2 := 1; memoout; // B0
if k < 1 then exit;
n := 1; b1 := -1; b2 := 2; memoout; // B1
if k < 2 then exit;
end;
// 計算範囲指定 偶数Noのみ計算 B2～
if (k <= MM) or ((k > MM) and (k mod 2 = 0)) then begin
// Seidel's algorithm for Tn
setlength(t, k - 1); // 配列確保 値クリア
t[0] := 1; // 分子係数初期値
q := 1; // 分母係数初期値
n := 2; // forto n=2 初期値B2
repeat
TntoBn; // ベルヌーイ数表示Tn = t[0]
for j := 0 to n - 2 do t[j + 1] := t[j] + t[j + 1]; // ->
t[n] := t[n - 1];
for j := n - 2 downto 0 do t[j + 1] := t[j] + t[j + 2]; // <-
t[0] := t[1];
inc(n, 2) // forto n=n+2 step2
until n >= k;
TntoBn; // ベルヌーイ数表示Tn = t[0]
end;
// 奇数No表示 "0/1" 表示
if (k mod 2 <> 0) then begin // 奇数no 0/1表示
n := k; b1 := 0; b2 := 1;
memoout; // ベルヌーイ数表示 0/1
end;
StopWatch.Stop;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
Edit1.text := '時間 = ' + intTostr(ElapsedMillseconds) + 'msec';
end;
//------------------------------------------------------------------------------
procedure TForm1.FormCreate(Sender: TObject);
begin
labeledEdit1.EditLabel.Caption := 'Bn n<=' + intTostr(NI);
end;
end.
Bernoulli_number_5.zip
各種プログラム計算例に戻る