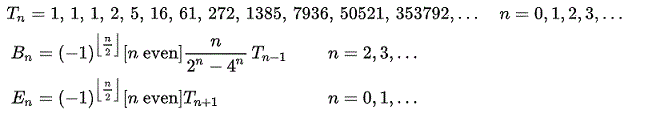
オイラー数 その4
オイラー数計算の高速演算に使用するアルゴリズムがWikipediaにあったのでプログラムを組んでみました。
Seidel's algorithm for Tn で
次のようになってます。
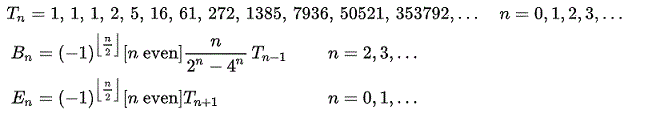
1
-> 1 1
2 2 1 <-
-> 2 4 5 5
16 16 14 10 5 <-
実際にプログラムを組む場合を考えてみます。
オイラー数は、
E0=1, E2=-1, E4=5, E6=-61, E8=1385
で上記数列の右側の値でが、符号がありません。
符号については、Noが4おきなので、後から簡単に設定ができます。
左側の値は、ベルヌーイ数計算用の係数となります。
オイラー数計算
[配列メモリーNo]
[0] [1] [2] [3] [4] [5] [6]
1 [0]=1 初期設定
1 1 -> [1]=[0] upから開始 forの値によりfor非実行
2 1 1 <- [0]=[1] down後表示 forの値によりfor非実行
1 2 2 -> {[1]=[1]+[0]} [2]=[1]
4 5 5 4 2 <- [3]=[2] {[2]=[3]+[1] [1]=[2]+[0]} [0]=[1]
5 10 14 16 16 -> {[1]=[1]+[0] [2]=[2]+[1] [3]=[3]+[2]} [4]=[3]
6 61 61 56 46 32 16 <- [5]=[4] {[4]=[5]+[3] [3]=[4]+[2] [2]=[3]+[1] [1]=[2]+[0]} [0]=[1]
61 122 178 224 256 272 272 -> {[1]=[1]+[0] [2]=[2]+[1] [3]=[3]+[2] [4]=[4]+[3] [5]=[5]+[4]} [6]=[5]
8 1385 <-
配列メモリーの[0]にEnの値が出る様にして、計算手順の表を作成しました。
矢印 -> <-
ワンセットforで実行され更にその中の { } 内が更にforで実行する部分となります。
最初の1は、計算に必要な初期設定値です、その為、最初のE0の値は、Tn計算のループから外れる為、別途先に表示します。
計算は、加算と減算のみなので非常に高速に計算が出来ます、E2000を0.4秒です。
基本プログラムは、わかり易いようにCで書いておきます。
/*********************************************************** Euler_numbers_c -- Euler (オイラー)数 ***********************************************************/ #include <stdio.h> #include <stdlib.h> #define N 22 /* 22以上はオーバーフロー */ int main() { int i, j, m, n; long long e; static long long t[N]; static char s[4] = " = "; n = 0; e = 1; printf(" E(%2d) = %lld\n", n, e); /* E0 */ t[0] = 1; for (n = 2; n <= N; n = n + 2) { /* for n = 2 to N step 2 E2~ */ for (j = 1; j <= n - 2; j++) t[j] += t[j - 1]; /* -> 最初は実行されない */ t[n - 1] = t[n - 2]; for (j = n - 2; j >= 1; j--) t[j] = t[j + 1] + t[j - 1]; /* <- 最初は実行されない */ t[0] = t[1]; e = t[0]; /* t[0] がEnの値 */ if ((n + 2) % 4 == 0) { e *= -1; s[3] = '\0'; /* n+2が4の倍数の時 En=-e */ } else s[3] = ' '; printf(" E(%2d)%s%lld\n", n, s, e); } printf("enterキーを押してください"); getchar(); return EXIT_SUCCESS; }
プログラム
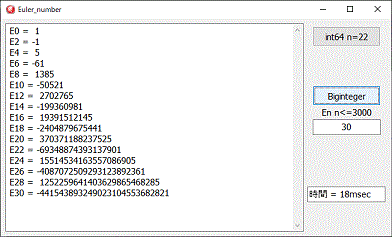
プログラムには、Bigintegerを使用します。
bigintegerの組み込みについては、ベルヌーイ数 その4を参照してください。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls, system.Diagnostics;
type
TForm1 = class(TForm)
BitBtn1: TBitBtn;
Memo1: TMemo;
BitBtn2: TBitBtn;
LabeledEdit1: TLabeledEdit;
Edit1: TEdit;
procedure BitBtn1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure BitBtn2Click(Sender: TObject);
private
{ Private 宣言 }
function Ninput(var n: integer): boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
{ Seidel's algorithm for Tn
0 1 2 3 4 5 6 7
Tn = 1,1,1,2,5,16,61, 272 Tn n=2,4,6,8
() forループ
n t[0] [1] [2] [3] [4] [5] [6] ->
1 [0]=1 初期値
1 1 -> [1]=[0] upから開始
2 1 1 <- [0]=[1]
1 2 2 -> ([1]=[1]+[0]) [2]=[1]
4 5 5 4 2 <- [3]=[2] ([2]=[3]+[1] [1]=[2]+[0]) [0]=[1]
5 10 14 16 16 -> ([1]=[1]+[0] ~ [3]=[3]+[2]) [4]=[3]
6 61 61 56 46 32 16 <- [5]=[4] ([4]=[5]+[3] ~ [1]=[2]+[0]) [0]=[1]
61 122 178 224 256 272 272 -> ([1]=[1]+[0] ~ [5]=[5]+[4]) [6]=[5]
}
uses Velthuis.BigIntegers;
const
Ni = 3000; // 最大オイラー数No Biginteger
// オイラー数計算 int64 n=22
procedure TForm1.BitBtn1Click(Sender: TObject);
const
k = 22;
var
t : array of int64;
e : int64;
j, m, n: integer;
mstr : string;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
// 値表示
procedure memoout;
begin
if e < 0 then mstr := ' = '
else mstr := ' = ';
memo1.Lines.Append('E' + intTostr(n) + mstr + inttostr(e));
end;
begin
StopWatch := TStopwatch.StartNew;
memo1.Clear;
n := 0; e := 1; memoout; // E0
// Seidel's algorithm for Tn
setlength(t, k); // 配列確保 オイラー数n 値クリア
t[0] := 1;
for m := 1 to k shr 1 do begin // for n=2 to k step 2 E2~
n := m shl 1; // n = m * 2
for j := 1 to n - 2 do t[j] := t[j] + t[j - 1]; // -> n=4から実行
t[n - 1] := t[n - 2];
for j := n - 2 downto 1 do t[j] := t[j + 1] + t[j - 1]; // <- n=4から実行
t[0] := t[1];
e := t[0]; // En = t[0]
if (n + 2) mod 4 = 0 then e := -e; // 符号設定
memoout; // 値表示
end;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
Edit1.text := '時間 = ' + intTostr(ElapsedMillseconds) + 'msec';
end;
// オイラーNo入力処理
function TForm1.Ninput(var n: integer): boolean;
var
c : integer;
begin
result := true;
val(labelededit1.Text, n, c);
if c <> 0 then begin
memo1.Text := 'オイラーNo に間違いがあります。';
result := false;
exit;
end;
if n < 0 then begin
memo1.Text := 'オイラーNoはゼロ以上にして下さい。';
result := false;
end;
if n > NI then begin
memo1.Text := 'オイラーNo が大きすぎます' + intTostr(NI) + '迄です。';
result := false;
end;
end;
// オイラー数計算 biginteger
procedure TForm1.BitBtn2Click(Sender: TObject);
const
MM = 30; // 一覧表示 No制限
var
t : array of biginteger;
e : biginteger;
j, m, n, k : integer;
mstr : string;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
// 値表示
procedure memoout;
begin
if e < 0 then mstr := ' = '
else mstr := ' = ';
memo1.Lines.Append('E' + intTostr(n) + mstr + e.ToString);
end;
begin
if not Ninput(k) then exit;;
StopWatch := TStopwatch.StartNew;
memo1.Clear;
if k <= MM then begin
n := 0; e := 1; memoout; // E0
end;
if k < 1 then exit;
// Seidel's algorithm for Tn
setlength(t, k); // 配列の確保 オイラー数n 値クリア
if (k <= MM) or ((k > MM) and (k mod 2 = 0)) then begin
t[0] := 1;
for m := 1 to k shr 1 do begin // for n=2 to k step 2 E2~
n := m shl 1; // n = m * 2
for j := 1 to n - 2 do t[j] := t[j] + t[j - 1]; // -> n=4から実行
t[n - 1] := t[n - 2];
for j := n - 2 downto 1 do t[j] := t[j + 1] + t[j - 1]; // <- n=4から実行
t[0] := t[1];
e := t[0]; // En = t[0]
if ((n <= MM) and (k <= MM)) or (k = n) then begin
if (n + 2) mod 4 = 0 then e := -e; // 符号の設定
memoout; // 値表示
end;
end;
end;
if k mod 2 <> 0 then begin // 奇数 0 表示
n := k; e := 0; memoout;
end;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
Edit1.text := '時間 = ' + intTostr(ElapsedMillseconds) + 'msec';
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
labeledEdit1.EditLabel.Caption := 'En n<=' + intTostr(NI);
end;
end.
![]() Euler_number_5.zip
Euler_number_5.zip
各種プログラム計算例に戻る