 縄跳び紐の計算式は、縄跳び紐の張力計算又は
縄跳び紐との接線その2を参照して下さい。
縄跳び紐の計算式は、縄跳び紐の張力計算又は
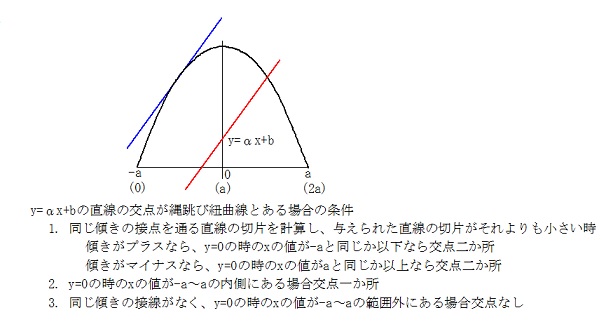
縄跳び紐との接線その2を参照して下さい。最初に指定された傾きαの接点があるどうか判別します。
その後 y=0時の xの値から交点が存在するか、有るなら二個か一個かを判別して、交点の検索をします。
縄跳び紐の曲線と直線の交点
縄跳び紐の曲線と、直線の交点を求めます。
連立方程式を解くことは難しいので、直線との交点があるかどうかの判別後、交点位置の検索を行います。
 縄跳び紐の計算式は、縄跳び紐の張力計算又は
縄跳び紐との接線その2を参照して下さい。
縄跳び紐の計算式は、縄跳び紐の張力計算又は
縄跳び紐との接線その2を参照して下さい。
最初に指定された傾きαの接点があるどうか判別します。
その後 y=0時の xの値から交点が存在するか、有るなら二個か一個かを判別して、交点の検索をします。
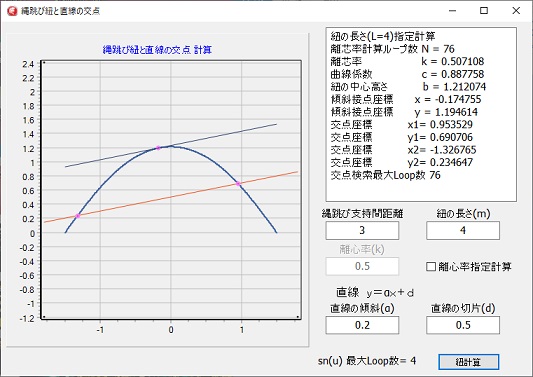 左図はプログラムの実行例で、指定された傾きαの接線がある場合は、接線を描画し、更に交点がある場合は、直線と交点を描画します。
左図はプログラムの実行例で、指定された傾きαの接線がある場合は、接線を描画し、更に交点がある場合は、直線と交点を描画します。
//----------------------------------------------------- // ヤコビの楕円関数と縄跳びの紐計算 // プログラムは下記の資料によります // http://fuchino.ddo.jp/yatsugatake/ellipticx.pdf // http://www.wannyan.net/scidog/ellipse/ellipse.pdf //----------------------------------------------------- unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) LabeledEdit10: TLabeledEdit; LabeledEdit11: TLabeledEdit; Memo1: TMemo; nawaBtn: TButton; Chart1: TChart; Series1: TLineSeries; Series2: TPointSeries; LabeledEdit1: TLabeledEdit; CheckBox1: TCheckBox; Label1: TLabel; LabeledEdit2: TLabeledEdit; Series4: TPointSeries; Series5: TLineSeries; LabeledEdit3: TLabeledEdit; Series3: TLineSeries; Label2: TLabel; procedure nawaBtnClick(Sender: TObject); procedure FormCreate(Sender: TObject); procedure CheckBox1Click(Sender: TObject); procedure CheckBox1KeyPress(Sender: TObject; var Key: Char); private { Private 宣言 } function calc_first_elliptic_integral(k, sinQ: double): double; function calc_second_elliptic_integral(k, sinQ: double): double; function jacobi_sn(u, k: double): double; function invertK(L, a2: double): double; function second_imperfect_elliptic_integral(Q, K: double; F: integer): double; procedure tangent(a2, k, b, c, alpha, ty: double; var x, y:double); procedure intersection(a2, k, b, c, alpha, z, lx, rx, ty, by, x0, y0: double); public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses Math; var V : integer; // sn(u, k)計算のLoop数 DBL_EPSILON : double; //------------------------------- // 第1種第2種不完全積分 // FBnKn[0] 第1種不完全積分解 // EBnKn[0] 第2種不完全積分解 // ランデン変換 // Q 角度 rad // K 離心率 // F = 1 第一種積分 F <> 1 第二種積分 //------------------------------- function TForm1.second_imperfect_elliptic_integral(Q, K: double; F: integer): double; var I, MI : integer; Kn : array of double; // Kn knd : array of double; // k'n N2SKn : array of double; // 2/(1+Kn) T2SKnd : array of double; // П2/(1+Kn') BRad : array of double; // β(rad) SinBn : array of double; // sinβn FBnKn : array of double; // F(βn,kn) EBnKn : array of double; // E(βn,kn) LnD : double; begin // K = 0 の時は円なのでpiの角度値rad。 if K = 0 then begin result := Q; exit; end; // 1 >= K > 0 の時 MI := 0; LnD := 0; setlength(kn, MI + 1); // kn kn[0] := K; while LnD <> Kn[MI] do begin // LnDとkn[]が同じ1になるまでくり返します LnD := Kn[MI]; inc(MI); setlength(kn, MI + 1); // kn kn[MI] := 2 * sqrt(Kn[MI - 1])/(1 + Kn[MI - 1]); end; setlength(kn, MI); // kn setlength(knd, MI); // k'n setlength(N2SKn, MI); // 2/(1+Kn) setlength(T2SKnd, MI); // П2/(1+Kn') setlength(BRad, MI); // β(rad) setlength(SinBn, MI); // sinβn setlength(FBnKn, MI); // F(βn,kn) setlength(EBnKn, MI); // E(βn,kn) dec(MI); knd[0] := 1; for I := 1 to MI do knd[I] := (1 - kn[I - 1]) / (1 + Kn[I - 1]); for I := 0 to MI do N2SKn[I] := 2 / (1 + kn[I]); T2SKnd[MI] := N2SKn[MI]; for I := MI - 1 downto 0 do T2SKnd[I] := T2SKnd[I + 1] * N2SKn[I]; BRad[0] := Q; for I := 1 to MI do BRad[I] := (arcsin(kn[I - 1] * sin(Brad[I - 1])) + Brad[I - 1]) / 2; for I := 0 to MI do SinBn[I] := sin(Brad[I]); result := (1 + sin(Brad[MI])) / cos(Brad[MI]); if result <= 0 then exit; // 0以下は自然対数の計算出来ません LnD := Ln(result); if F = 1 then begin // 第一種指定なら result := T2SKnd[0] * LnD; // 第一種 exit; end; for I := 0 to MI do FBnKn[I] := T2SKnd[I] * LnD; EBnKn[MI] := sin(Brad[MI]); for I := MI - 1 downto 0 do EBnKn[I] := (2 * EBnKn[I + 1] + 2 * knd[I + 1] * FBnKn[I + 1]) / (1 + knd[I + 1]) - kn[I] * SinBn[I]; result := EBnKn[0]; // 第二種 end; // 第一種楕円積分 ルーチン // sin(φ) 単位 function TForm1.calc_first_elliptic_integral(k, sinQ: double): double; var asin : double; begin asin := abs(sinQ); if (k >= 1) and (asin >= 1) then // 積分出来ない値だったら result := MaxDouble // double最大値セット∞の代わり else result := second_imperfect_elliptic_integral(arcsin(asin), K, 1); // 第一種不完全積分 if sinQ < 0 then result := -result; end; // 第二種楕円積分 ルーチン // sin(φ) 単位 function TForm1.calc_second_elliptic_integral(k, sinQ: double): double; var asin : double; begin asin := abs(sinQ); if (K >= 1) and (sinQ >= 1) then // 積分出来ない値だったら result := 1 else result := second_imperfect_elliptic_integral(arcsin(asin), K, 2); // 第二種不完全積分 if sinQ < 0 then result := -result; end; // Jacobi関数 Jacobi sn(u, k) function TForm1.Jacobi_sn(u, k: double): double; const KN = 30; var a: array of double; g: array of double; c: array of double; two_n : double; phi : double; half : double; i, j : integer; begin half := 1 / 2; if k = 0 then begin result := sin(u); exit; end; if k = 1 then begin result := sin(2 * arctan(exp(u)) - pi / 2); exit; end; setlength(a, KN + 1); setlength(g, KN + 1); setlength(c, KN + 1); a[0] := 1; g[0] := sqrt(1 - k * k); c[0] := k; two_n := 1; for i := 0 to KN - 1 do begin if abs(a[i] - g[i]) < a[i] * DBL_EPSILON then break; two_n := two_n + two_n; a[i + 1] := half * (a[i] + g[i]); g[i + 1] := sqrt(a[i] * g[i]); c[i + 1] := half * (a[i] - g[i]); end; V := i; phi := two_n * a[i] * u; for j := i downto 1 do phi := half * (phi + arcsin(c[j] * sin(phi) / a[j])); result := sin(phi); end; // 傾きαを指定された直線の接点位置の計算 // 微分式 sn'z=√((1-sn^2z)(1-k^2sn^2z)) よりsnz計算 // 曲線の傾斜α=sn'z b/c // a2 縄跳びの支持間距離 // k 離心率 // b 縄跳び紐の高さ // c 曲線係数 // alpha 傾斜 // ty グラフ上限値 // x,y 接点座標 procedure TForm1.tangent(a2, k, b, c, alpha, ty: double; var x, y:double); var dx, u, snzk : double; a : double; dy, z : double; A1, B1 : double; a0, b0, c0 : double; begin // 端点最大傾斜(b / c)に対するαの確認 if abs(alpha) > (b / c) then begin // 端点の傾きより直線の傾きが大きい場合 x := 0; y := -1; // 接線無し exit; end; a := a2 / 2; // 紐中心位置 // 直線の傾αと離心率kから楕円関数snzkの計算 A1 := alpha * c / b; a0 := k * k; b0 := -1 - a0; c0 := 1 - A1 * A1; B1 := (-b0 - sqrt(b0 * b0 - 4 * a0 * c0)) / 2 / a0; snzk := sqrt(B1); // sn(z,k) // 座標計算 u := calc_first_elliptic_integral(k, snzk); // 第一種不完全楕円積分 θ(rad)=arcsin(snzk) x := u * c; // x座標 x := x - a; // x座標を中心座標に変換 y := snzk * b; // x位置のyの値 if alpha < 0 then x := - x; // 傾きがマイナスの場合はxが逆方向 Series4.AddXY(x, y); // グラフに接点の位置追加 memo1.Lines.Add('傾斜接点座標 x = ' + floatTostrF(x, ffFixed, 10, 6)); memo1.Lines.Add('傾斜接点座標 y = ' + floatTostrF(y, ffFixed, 10, 6)); // 接線の描画 z := y - alpha * x; // 切片の計算 dx := 0 - a; // 始点x dy := alpha * dx + z; // 始点y if dy > ty then begin // yの値がグラフの上限を超えたら調整 dx := (ty - z) / alpha; dy := ty; end; Series5.AddXY(dx, dy); // グラフに追加 dx := a2 - a; // 終点x dy := alpha * dx + z; // 終点y if dy > ty then begin // yの値がグラフの上限を超えたら調整 dx := (ty - z) / alpha; dy := ty; end; Series5.AddXY(dx, dy); // グラフに追加 end; // a2 縄跳びの支持間距離 // k 離心率 // b 縄跳び紐の高さ // c 曲線係数 // alpha 傾斜 // z 切片 // lx, rx グラフ左限右限 // ty, by グラフ上限下限 // x0, y0 接点座標 procedure TForm1.intersection(a2, k, b, c, alpha, z, lx, rx, ty, by, x0, y0: double); const KN = 8; Mi = 1000; var i : integer; a, z0 : double; x, y : double; xs, ys : double; xe, ye : double; yl : double; CRF : byte; // 0 交点なし 1 交点一か所 2 交点二か所 3 原点通過水平線 dx, u : double; N, Mn : integer; ax : double; // 交点表示 procedure datoutput(x, y: double; N: integer); begin Series4.AddXY(x, y); // グラフに追加 memo1.Lines.Add('交点座標 x' + intTostr(N) + '= ' + floatTostrF(x, ffFixed, 10, 6)); memo1.Lines.Add('交点座標 y' + intTostr(N) + '= ' + floatTostrF(y, ffFixed, 10, 6)); end; begin CRF := 0; a := a2 / 2; // 傾斜がゼロでない場合 if alpha <> 0 then begin x := - z / alpha; // y=0の時のxの値計算 if y0 < 0 then begin // 指定傾斜の接点が無いとき if (-a <= x ) and (x <= a) then CRF := 1 // y=0 のx座標が紐の支持間内の時交点一か所 else CRF := 0; // 支持間外の時交点無し end else begin // 指定傾斜の接点がある場合 z0 := y0 - x0 * alpha; // 接点を通る直線の切片 ax := a + DBL_EPSILON * a; if z > 0 then ax := a - DBL_EPSILON * a; // 演算誤差による判定ミス修正の為の値 交点有り側に設定 if (z < z0) then begin // 接線の切片より指定直線の切片が小さい場合 if (x <= -ax) and (alpha >= 0) then CRF := 2; // 傾斜角がプラスの時で、xの値が左端より外の時交点二か所 if (x >= ax) and (alpha <= 0) then CRF := 2; // 傾斜角がマイナスの時で、xの値が右端より外の時交点二か所 if (-ax < x) and (x < ax) then CRF := 1; // xの値が支持間内の時交点一か所 end; end; end else begin // 傾斜がゼロの時 if (0 < z) and (z <= b) then CRF := 2; // 紐の曲線の高さ範囲なら交点二か所 if 0 = z then CRF := 3; // 原点通過水平線 end; Mn := 0; dx := a2 / KN; N := 1; if CRF = 0 then memo1.Lines.Add('交点無し'); if (CRF = 1) and (alpha > 0) then begin // 交点一か所で傾斜プラスの時の交点検索 x := 0; // 左端から検索 i := 0; repeat x := x + dx; // 右へ検索 u := x / c; // F(α,k)=u y := b * jacobi_sn(u, k); // x位置のyの値 yl := alpha * (x - a) + z; // 直線のx位置のyの値 if yl > y then begin x := x - dx; dx := dx / 2; end; inc(i); until (dx <= DBL_EPSILON * a) or (i > Mi); x := x - a; datoutput(x, y, N); Mn := i; end; if (CRF = 1) and (alpha < 0) then begin // 交点一か所で傾斜マイナスの時の交点検索 x := a2; // 右端から検索 i := 0; repeat x := x - dx; // 左へ検索 u := x / c; // F(α,k)=u y := b * jacobi_sn(u, k); // x位置のyの値 yl := alpha * (x - a) + z; // 直線のx位置のyの値 if yl > y then begin x := x + dx; dx := dx / 2; end; inc(i); until (dx <= DBL_EPSILON * a) or (i > Mi); x := x - a; datoutput(x, y, N); if i > Mn then Mn := i; end; if CRF = 2 then begin // 交点が二か所の時の交点検索 x := x0 + a; // 開始点を接線位置にセット i := 0; repeat x := x + dx; // 右へ検索 u := x / c; // F(α,k)=u y := b * jacobi_sn(u, k); // x位置のyの値 yl := alpha * (x - a) + z; // 直線のx位置のyの値 if yl > y then begin x := x - dx; dx := dx / 2; end; inc(i); until (dx <= DBL_EPSILON * a) or (i > Mi); // 収束判定 x := x - a; datoutput(x, y, N); inc(N); if i > Mn then Mn := i; x := x0 + a; // 開始点を接線位置にセット i := 0; dx := a2 / KN; repeat x := x - dx; // 左へ検索 u := x / c; // F(α,k)=u y := b * jacobi_sn(u, k); // x位置のyの値 yl := alpha * (x - a) + z; // 直線のx位置のyの値 if yl > y then begin x := x + dx; dx := dx / 2; end; inc(i); until (dx <= DBL_EPSILON * a) or (i > Mi); // 収束判定 if i > Mn then Mn := i; x := x - a; datoutput(x, y, N); end; if CRF = 3 then begin // 水平直線で原点を通る場合 x := -a; y := 0; N := 1; datoutput(x, y, N); x := a; N := 2; datoutput(x, y, N); end; // 直線の描画 // 直線がグラフ内か確認と直線描画用座標計算 ys := alpha * lx + z; xs := lx; if ys > ty then begin xs := (ty - z) / alpha; ys := ty; end; if ys < by then begin xs := (by - z) / alpha; ys := by; end; xe := rx; ye := alpha * rx + z; if ye > ty then begin xe := (ty - z) / alpha; ye := ty; end; if ye < by then begin xe := (by - z) / alpha; ye := by; end; // 直線がグラフ内なら描画 if (xs >= lx) and (xe <= rx) and (ys >= by) and (ys <= ty) and (ye >= by) and (ye <= ty) then begin Series3.AddXY(xs, ys); // グラフに直線追加始点 Series3.AddXY(xe, ye); // グラフに直線追加終点 end else memo1.Lines.Add('指定された直線はグラフ外'); if Mn <> 0 then memo1.Lines.Add('交点検索最大Loop数 ' + intTostr(Mn)); end; // 離芯率kの計算 // L=4a/k'^2*E/K-2aのaとLが既知なのでkの値を求めます。 // L 紐の長さ // a2 支持間距離 function TForm1.invertK(L, a2: double): double; const KN = 500; var c, fc : double; k, E, Fk : double; dk : double; N : integer; begin a2 := abs(a2); c := (L + a2) / a2 / 2; // L=4a/k'^2*E/K-2a から判定用固定値計算 k := 0; // 離心率初期値 dk := 1 / 2; // Δk N := 0; repeat inc(N); k := k + dk; // k+Δk if k >= 1 then k := 1 - DBL_EPSILON; // kが1に成った時1から僅かに小さくします。 E := calc_second_elliptic_integral(k, 1); // 第二種完全積分 Fk := calc_first_elliptic_integral(k, 1); // 第一種完全積分 fc := E / Fk / (1 - k * k); // 判定比較値計算 if fc > c then begin // 大きかったら k := k - dk; // Δk減算 dk := dk / 2; // Δk 2分の1 end; until (dk <= DBL_EPSILON * k) or (N > KN); // 収束判定 memo1.Lines.Add('離芯率計算ループ数 N = ' + intTostr(N)); result := k; end; // 縄跳びの縄弛み計算 procedure TForm1.nawaBtnClick(Sender: TObject); const kN = 400; var k : double; // k 離心率 ch : integer; a, a2 : double; // a2 紐支持間 a = a2 / 2 Fkd : double; // Fkd 第一種完全積分 b, u : double; // b 縄高さ F(θ,k)=u c, L : double; // c 曲線係数 L 縄の指定長さ i : integer; x, y, dx : double; // x,y 縄上の座標 dx = Δx snuk : double; // snuk := jacobi_sn(u, k) ty, by : double; // ty グラフ上限 by グラフ下限 lx, rx : double; // lx グラフ左限 rx グラフ右限 def, ddf : double; // グラフ余白 Ek : double; // Ek 第二種完円積分 Lk : double; // LK 離心率指定 紐長さ alpha : double; // α 直線の傾斜 z : double; // z 直線の切片 x0, y0 : double; // x0,y0 傾斜αの接点 begin V := 0; k := 0; L := 0; val(Labelededit10.Text, a2, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐支持間に間違いがあります。','注意',0); exit; end; val(Labelededit2.Text, alpha, ch); if ch <> 0 then begin application.MessageBox('直線の傾きに間違いがあります。','注意',0); exit; end; val(Labelededit3.Text, z, ch); if ch <> 0 then begin application.MessageBox('直線の切片に間違いがあります。','注意',0); exit; end; if checkbox1.Checked then begin val(LabeledEdit1.Text, k, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐離心率Kに間違いがあります。','注意',0); exit; end; if k >= 1 then begin application.MessageBox('k(離心率)のは1以下にして下さい。','注意',0); exit; end; if k < 0 then begin application.MessageBox('k(離心率)の値にマイナスはありません。','注意',0); exit; end; end else begin val(LabeledEdit11.Text, L, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐の長さに間違いがあります。','注意',0); exit; end; if L <= abs(a2) then begin application.MessageBox('紐の長さは支持間より長くしてください。','注意',0); exit; end; end; memo1.Clear; if not checkbox1.Checked then begin memo1.Lines.Add('紐の長さ(L=' + floatTostr(L) + ')指定計算'); k := invertK(L, a2); // 離芯率kの計算 memo1.Lines.Add('離芯率 k = ' + floatTostrF(k, ffFixed, 10, 6)); end else memo1.Lines.Add('離心率(k=' + floatTostr(k) + ')指定計算'); Fkd := calc_first_elliptic_integral(k, 1); // 第一種完全積分90° // 各種計算 a := a2 / 2; // a 中央位置90°分 c := a / Fkd; // 積分値に対する曲線係数 b := 2 * k / (1 - k * k) * c; // 最大高さ 中央の位置 memo1.Lines.Add('曲線係数 c = ' + floatTostrF(c, ffFixed, 10, 6)); memo1.Lines.Add('紐の中心高さ b = ' + floatTostrF(b, ffFixed, 10, 6)); // 紐の長さ計算 中間位置の計算は出来ません if checkbox1.Checked then begin Ek := calc_second_elliptic_integral(k, 1); // 第二種完円積分90° Lk := 4 * c * Ek / (1 - k * k) - a2; // 弧(紐)の長さ計算 memo1.Lines.Add('紐の長さ L = ' + floatTostrF(Lk, ffFixed, 10, 6)); end; Series1.Clear; Series2.Clear; Series3.Clear; Series4.Clear; Series5.Clear; // グラフスケール設定 if abs(a2) > b then begin ddf := a2 / 10; def := (a2 - b) / 2; ty := b + def + ddf; by := 0 - def - ddf; rx := a + ddf; lx := -a - ddf; end else begin ddf := b / 10; def := (b - a2) / 2; ty := b + ddf; by := 0 - ddf; rx := a + def + ddf; lx := -a - def - ddf; end; // グラフのスケール設定値セット Series2.AddXY(lx, ty); Series2.AddXY(lx, by); Series2.AddXY(rx, by); application.ProcessMessages; // グラフ表示待ち // グラフ作図 dx := a2 / KN; // ΔX // 0~KN 計算作図 for i := 0 to KN do begin x := i * dx; // x位置 u := x / c; // F(θ,k)=u snuk := jacobi_sn(u, k); // jacobi_sn ヤコビの楕円関数 y := snuk * b; // x位置のyの値 Series1.AddXY(x - a, y); // グラフに追加 end; application.ProcessMessages; tangent(a2, k, b, c, alpha, ty, x0, y0); // 接点座標x0,y0の計算 intersection(a2, k, b, c, alpha, z, lx, rx, ty, by, x0, y0); // 交点の計算 Label1.Caption := 'sn(u) 最大Loop数= ' + intTostr(V); end; procedure TForm1.CheckBox1Click(Sender: TObject); begin if CheckBox1.Checked then begin labeledEdit1.Enabled := True; labeledEdit11.Enabled := False; end else begin labeledEdit1.Enabled := False; labeledEdit11.Enabled := True; end; end; procedure TForm1.CheckBox1KeyPress(Sender: TObject; var Key: Char); begin if CheckBox1.Checked then CheckBox1.Checked := False else CheckBox1.Checked := True; end; procedure TForm1.FormCreate(Sender: TObject); const IM = 50; var x, y, z : double; i : integer; begin labeledEdit1.Enabled := False; // 桁落ち判定値設定 i := 0; x := 1; y := 1 / 4194304; // 4194304 = 2^22 repeat y := y / 2; z := x + y; // 桁落ち確認加算 inc(i); until (z = 1) or (i > IM) ; // 桁落ちするまで繰り返し DBL_EPSILON := y * 2; // DBL_EPSILON 桁落ち判定値 end; end.