縄跳び紐の張力計算
ヤコビの楕円関数の計算に縄跳び紐の計算が有ります。
縄跳び紐の回転時の形状は、ヤコビの楕円関数ｓｎの計算を使用します。
此処では、縄跳び紐の張力の計算をします。
張力の計算には、第一種楕円積分を利用する方法と、二次方程式を利用する方法が有ったので、両方の計算をしてみました。
二次方程式を利用する方法でも、cの値の計算に第一種楕円積分を使用しているので、両方とも第一種楕円積分を利用していることは変わりません。
紐の張力は水平方向の張力を計算して、紐端点の紐の角度により、紐の端点の張力を求めます。
実際には、重力加速度の影響があるのですが、計算に入っていません。
紐を廻す為には、端点も小さな回転をしているし、空気の抵抗があるので、厳密な計算は難しく、ここでは全て無視をして向心力だけの計算をしています。
紐の長さ計算には、第一種楕円積分と第二種楕円積分を利用します。
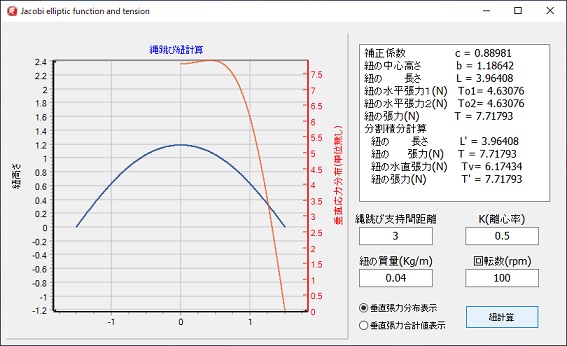左図は、Ｘ方向を分割計算して、垂直張力の分布を表示しています。
分割計算の場合、垂直方向の値を求めるのが容易だからです。
中央部分が少し凹んでいるのは、Ｘ方向に対して、紐が水平に近くなるため、傾斜のある部分より、紐の長さが短くなる為です。
張力のグラフは、分割計算により表示しています。
表示方法を変更することにより、中央からの合計値の表示も可能です。
紐の水平張力１は、第一種楕円積分による張力計算、紐の水平張力２は、第一種楕円積分と二次方程式利用による張力計算です。
プログラム
//----------------------------------------------------- // ヤコビの楕円関数と縄跳びの紐計算 // http://fuchino.ddo.jp/yatsugatake/ellipticx.pdf //----------------------------------------------------- unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) LabeledEdit10: TLabeledEdit; LabeledEdit11: TLabeledEdit; Memo1: TMemo; nawaBtn: TButton; Chart1: TChart; Series1: TLineSeries; Series2: TPointSeries; massEdit: TLabeledEdit; rotational_speed_Edit: TLabeledEdit; Series3: TLineSeries; RadioButton1: TRadioButton; RadioButton2: TRadioButton; procedure nawaBtnClick(Sender: TObject); private { Private 宣言 } function RJ(x1, y1, z1, p1: double): double; function RF(x1, y1, z1: double): double; function calc_first_elliptic_integral(k, dpi: double; var ALFRG : byte): double; function calc_second_elliptic_integral(k, dpi: double): double; function jacobi_sn(u, k: double): double; function Jacobi_am(u, k: double): double; procedure tension(a, k, b, c: double); public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses Math; // Carlson's Elliptic Integral RJ function TForm1.RJ(x1, y1, z1, p1: double): double; var s, fa, rj, rk : double; la, mu : double; al, be : double; r1, a1, b1 : double; a2, b2, mv, s1 : double; rc, r0 : double; s12, s13, s14 : double; s15, s16 : double; x2, y2, z2 : double; x3, y3, z3 : double; s2, s3, p2, p3 : double; s4, s5 : double; x31, y31, z31, p31 : double; s22, s23, s2s3 : double; procedure rcab; begin rc := 1; a1 := al; b1 := be; repeat r1 := rc; la := 2 * sqrt(a1 * b1) + b1; a2 := (a1 + la) / 4; b2 := (b1 + la) / 4; mv := (a1 + 2 * b1) / 3; s1 := (b1 - a1) / (3 * mv); s12 := s1 * s1; s13 := s12 * s1; s14 := s13 * s1; s15 := s14 * s1; s16 := s15 * s1; rc := (1 + 3 * s12 / 10 + s13 / 7 + 3 * s14 / 8 + 9 * s15 / 22 + 159 * s16 / 208) / sqrt(mv); a1 := a2; b1 := b2; until r1 = rc; end; function ss: double; begin x31 := x31 * x3; y31 := y31 * y3; z31 := z31 * z3; p31 := p31 * p3; result := (x31 + y31 + z31 + p31); end; begin s := 0; fa := 3; rj := 0; repeat r0 := rj; la := sqrt(x1 * y1) + sqrt(x1 * z1) + sqrt(y1 * z1); mu := (x1 + y1 + z1 + 2 * p1) / 5; x2 := (x1 + la) / 4; y2 := (y1 + la) / 4; z2 := (z1 + la) / 4; p2 := (p1 + la) / 4; x3 := 1 - x1 / mu; y3 := 1 - y1 / mu; z3 := 1 - z1 / mu; p3 := 1 - p1 / mu; x31 := x3; y31 := y3; z31 := z3; p31 := 2 * p3; s2 := ss / 4; s3 := ss / 6; s4 := ss / 8; s5 := ss / 10; al := (sqrt(x1) + sqrt(y1) + sqrt(z1)) * p1 + sqrt(x1 * y1 * z1); al := al * al; be := p1 * (p1 + la) * (p1 + la); rcab; s22 := 3 * s2 * s2 / 22; s23 := s2 * s2 * s2 / 10; s2s3 := s2 * s3 * 3 / 13; s := s + fa * rc; rk := 1 + 3 * s2 / 7 + s3 / 3 + s22 + s2s3 + 3 * s4 / 11 + 3 * s5 / 13 - s23; fa := fa / 4; mu := sqrt(1 / (mu * mu * mu)); rj := s + fa / 4 * (rk + 3 * s3 * s3 / 10 + 3 * s2 * s4 / 5) * mu; x1 := x2; y1 := y2; z1 := z2; p1 := p2; until rj = r0; result := rj; end; // Carlson's Elliptic Integral RF function TForm1.RF(x1, y1, z1: double): double; var la, mu : double; x2, y2, z2 : double; x3, y3, z3 : double; s2, s3 : double; r0, rf : double; s22, s23, s2s3, s32 : double; begin rf := 0; repeat r0 := rf; la := sqrt(x1 * Y1) + sqrt(x1 * z1) + sqrt(y1 * z1); mu := (x1 + y1 + z1) / 3; x2 := (x1 + la) / 4; y2 := (y1 + la) / 4; z2 := (z1 + la) / 4; x3 := 1 - x2 / mu; y3 := 1 - y2 / mu; z3 := 1 - z2 / mu; s2 := (x3 * x3 + y3 * y3 + z3 * z3) / 4; s3 := (x3 * x3 * x3 + y3 * y3 * y3 + z3 * z3 * z3) / 6; s22 := s2 * s2 / 6; s23 := 5 * s2 * s2 * s2 / 26; s32 := 3 * s3 * s3 / 26; s2s3 := s2 * s3 * 3 / 11; rf := (1 + s2 / 5 + s3 / 7 + s22 + s2s3 + s23 + s32) / sqrt(mu); x1 := x2; y1 := y2; z1 := z2; until rf = r0; result := rf; end; // 第一種楕円積分 ルーチン // π/2迄 function TForm1.calc_first_elliptic_integral(k, dpi: double; var ALFRG : byte): double; var s, s2 : double; c2 : double; rf0 : double; k2 : double; eq : double; fqk : double; dpib : double; begin ALFRG := 0; fqk := 0; dpib := dpi; dpi := abs(dpi); s := sin(dpi); // sin(φ) s2 := s * s; // sin~2(φ) eq := dpi; k2 := k * k; // k^2 if ((1 - k2 * s2) <= 0) then begin // 1-K^2*sin^2(φ) = 0 K=1 φ=π/2 なら ALFRG := 1; end else begin // 1-K^2*sin^2(φ) > 0 なら c2 := cos(eq) * cos(eq); // cos^2(φ') s := sin(eq); // sin(φ') s2 := s * s; // sin^2(φ') rf0 := RF(c2, 1 - k2 * s2, 1); fqk := s * rf0; // F(φ',K) = rf0 * sin(φ') if dpib < 0 then fqk := - fqk; // 積分範囲の符号で積分値の符号設定 end; result := fqk; end; // 第二種楕円積分 ルーチン // プラス側のみ pi / 2 迄 function TForm1.calc_second_elliptic_integral(k, dpi: double): double; const KS = 1E-15; var s, s2, s3 : double; c2 : double; rf0 : double; k2 : double; eq : double; rd0 : double; eek : double; begin eq := dpi; k2 := k * k; // k^2 if (eq < pi / 2) or ((1 - abs(K)) >= KS) then begin // if (eqd < 90) or (abs(K) < 1) then begin if (1 - abs(K)) >= KS Then begin // if abs(K) < 1 Then begin c2 := cos(eq) * cos(eq); s := sin(eq); s2 := s * s; s3 := s2 * s; rf0 := RF(c2, 1 - k2 * s2, 1); rd0 := RJ(c2, 1 - k2 * s2, 1, 1); eek := s * rf0 - k2 / 3 * s3 * rd0; end else eek := sin(eq); end else eek := 1; result := eek; end; // 振幅関数 am(u, k) function TForm1.Jacobi_am(u, k: double): double; const N = 30; EPSILON = 1E-15; var a: array[0..N] of Extended; g: array[0..N] of Extended; c: array[0..N] of Extended; two_n : Extended; phi : Extended; half : Extended; i, j : integer; begin half := 1 / 2; if k = 0 then begin result := u; exit; end; if k = 1 then begin result := 2 * arctan(exp(u)) - pi / 2; exit; end; a[0] := 1; g[0] := sqrt(1 - k * k); c[0] := k; two_n := 1; for i := 0 to N do begin if abs(a[i] - g[i]) < a[i] * EPSILON then break; two_n := two_n + two_n; a[i + 1] := half * (a[i] + g[i]); g[i + 1] := sqrt(a[i] * g[i]); c[i + 1] := half * (a[i] - g[i]); end; phi := two_n * a[i] * u; for j := i downto 1 do phi := half * (phi + arcsin(c[j] * sin(phi) / a[j])); result := phi; end; // ヤコビの楕円関数 sn(u, k) function TForm1.jacobi_sn(u, k: double):double; begin result := sin(Jacobi_am(u, k)); end; // 紐の張力 procedure TForm1.tension(a, k, b, c: double); const KN = 10000; var ch : integer; p, w : double; R, T : double; Tv, T0, g : double; u : double; a0, b0, c0 : double; i : integer; x, y : double; xb, yb : double; rx, ty : double; dx : double; dx2 : double; snuk : double; lp, fp : double; Sl, Th : double; Ke : double; FR : byte; a2 : double; begin val(massEdit.Text, p, ch); if ch <> 0 then begin application.MessageBox('紐の質量に間違いがあります。','注意', 0); exit; end; val(rotational_speed_Edit.Text, R, ch); if ch <> 0 then begin application.MessageBox('回転数に間違いがあります。','注意', 0); exit; end; w := R / 60 * pi * 2; // 角速度 ω g := p * w * w; // γ=ρ*ω^2 // 水平張力計算１ FR := 0; a2 := a + a; Ke := calc_first_elliptic_integral(k, pi / 2, FR); // 第一種完全積分 T0 := g * a2 * a2 / 4 / (1 - k * k) / Ke / Ke; // 水平張力 memo1.Lines.Add('紐の水平張力１(N) To1= ' + floatTostrF(T0, ffFixed, 10, 5)); // T := T0 * sqrt(b * b / c / c + 1); // 水平張力計算２ if b <> 0 then begin a0 := -1 / c / c; b0 := g; c0 := g * g * b * b / 4; T0 := (-b0 - sqrt(b0 * b0 - 4 * a0 * c0)) / 2 / a0; // 二次方程式の解法 end else T0 := 0; memo1.Lines.Add('紐の水平張力２(N) To2= ' + floatTostrF(T0, ffFixed, 10, 5)); T := T0 * sqrt(b * b / c / c + 1); // T0 / cosθ memo1.Lines.Add('紐の張力(N) T = ' + floatTostrF(T, ffFixed, 10, 5)); memo1.Lines.Add('分割積分計算'); a0 := sqrt(c * c / b / b + 1); // b0 := sqrt(b) / c / c; dx := a / KN; dx2 := dx / 2; Tv := 0; Th := 0; xb := a; u := xb / c; // F(α,k)=u // jacobi_sn ヤコビの楕円関数 snuk := jacobi_sn(u, k); yb := snuk * b; // x位置のyの値 Sl := 0; for i := KN downto 0 do begin x := i * dx - dx2; // x位置 u := x / c; // F(α,k)=u // jacobi_sn ヤコビの楕円関数 snuk := jacobi_sn(u, k); y := snuk * b; // x位置のyの値 rx := (x - xb); // Δx ty := (y - yb); // Δy if i = 0 then begin rx := 0 - xb; ty := 0 - yb; end; lp := sqrt(rx * rx + ty * ty); // Δl Sl := Sl + lp; // L fp := lp * (y + yb) * 0.5 * g; // F 向心力= mrω^2 if Radiobutton1.Checked then if i < KN then Series3.AddXY(-x + a, fp * KN); // グラフに追加 Tv := Tv + fp; // 垂直張力 if y <> 0 then begin fp := fp * a0; Th := Th + fp; end; xb := x; yb := y; if Radiobutton2.Checked then Series3.AddXY(-x + a, Tv); // グラフに追加 end; Sl := Sl * 2; memo1.Lines.Add(' 紐の 長さ L'' = ' + floatTostrF(Sl, ffFixed, 10, 5)); memo1.Lines.Add(' 紐の 張力(N) T = ' + floatTostrF(Th, ffFixed, 10, 5)); memo1.Lines.Add(' 紐の水直張力(N) Tv= ' + floatTostrF(Tv, ffFixed, 10, 5)); if b = 0 then T := 0 else T := Tv * sqrt(c * c / b / b + 1); // Tv / cos(pi/2 - θ) // a0 := arctan(b / c); // T := tv / cos(pi/ 2 - a0); memo1.Lines.Add(' 紐の張力(N) T'' = ' + floatTostrF(T, ffFixed, 10, 5)); end; // 縄跳びの縄弛み計算 procedure TForm1.nawaBtnClick(Sender: TObject); const kN = 200; var ALFRG : byte; k : double; ch : integer; a, a2 : double; fkd, b, u : double; c, L : double; Ek : double; i : integer; x, y, dx : double; snuk : double; ty, by : double; lx, rx : double; def, ddf : double; begin val(Labelededit10.Text, a2, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐支持間に間違いがあります。','注意',0); exit; end; val(LabeledEdit11.Text, k, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐離心率Ｋに間違いがあります。','注意',0); exit; end; if k = 0 then begin application.MessageBox('k(離心率)の値がゼロでは張力計算出来ません。','注意',0); exit; end; if abs(k) > 1 then begin application.MessageBox('k(離心率)の最大値は±１です。','注意',0); exit; end; memo1.Clear; ALFRG := 0; fkd := calc_first_elliptic_integral(k, pi / 2, ALFRG); // 2 * 第一種楕円積分(90°) if ALFRG = 1 then begin memo1.Lines.Add('支持間の距離係数 第一種楕円積分の'); memo1.Lines.Add('積分用の値がゼロになります。'); memo1.Lines.Add('Kの値を１以下にして下さい。'); exit; end; if radiobutton1.Checked then Chart1.RightAxis.Title.Caption := '垂直応力分布(単位無し)' else Chart1.RightAxis.Title.Caption := '垂直応力積分値'; // 各種計算 a := a2 / 2; c := a / fkd; // 積分値に対する補正係数 b := 2 * k / (1 - k * k) * c; // 最大値 中央の位置 Ek := calc_second_elliptic_integral(k, pi / 2); // 第二種楕円積分(90°) L := 4 * c * Ek / (1 - k * k) - a2; // 弧の長さ計算 memo1.Lines.Add('補正係数 c = ' + floatTostrF(c, ffFixed, 10, 5)); memo1.Lines.Add('紐の中心高さ b = ' + floatTostrF(b, ffFixed, 10, 5)); memo1.Lines.Add('紐の 長さ L = ' + floatTostrF(L, ffFixed, 10, 5)); Series1.Clear; Series2.Clear; Series3.Clear; // グラフスケール設定 if abs(a2) > b then begin ddf := a2 / 10; def := (a2 - b) / 2; ty := b + def + ddf; by := 0 - def - ddf; rx := a + ddf; lx := -a - ddf; end else begin ddf := b / 10; def := (b - a2) / 2; ty := b + ddf; by := 0 - ddf; rx := a + def + ddf; lx := -a - def - ddf; end; // グラフのスケール設定値セット Series2.AddXY(lx, ty); Series2.AddXY(lx, by); Series2.AddXY(rx, by); application.ProcessMessages; // グラフ作図と分割積分 dx := a / KN; // ΔX // 0～KN 計算作図 for i := 0 to KN do begin x := i * dx; // x位置 u := x / c; // F(α,k)=u // jacobi_sn ヤコビの楕円関数 snuk := jacobi_sn(u, k); y := snuk * b; // x位置のyの値 Series1.AddXY(x - a, y); // グラフに追加 end; for i := KN + 1 downto 0 do begin x := i * dx; // x位置 u := x / c; // F(α,k)=u // jacobi_sn ヤコビの楕円関数 snuk := jacobi_sn(u, k); x := a2 - x; y := snuk * b; // x位置のyの値 Series1.AddXY(x - a, y); // グラフに追加 end; application.ProcessMessages; // 張力計算 tension(a, k, b, c); end; end.
jacobi_elliptic_skipping_rope.zip