楕円弧部各種計算
楕円弧長さ、楕円弧面積、楕円弦長さ、楕円扇面積 計算
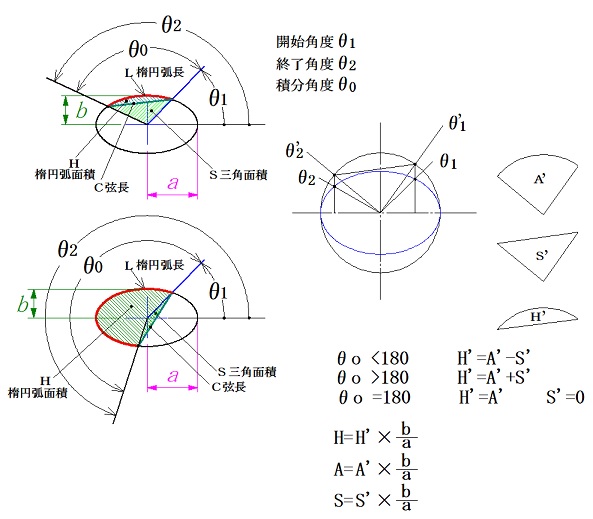 楕円に対して、指定された角度の範囲に対して、楕円弧長さ、楕円弧面積、楕円弦長さ、楕円扇面積の計算をします。
楕円に対して、指定された角度の範囲に対して、楕円弧長さ、楕円弧面積、楕円弦長さ、楕円扇面積の計算をします。
楕円弧長の計算には楕円積分が必要なので、楕円の周長2を参照してください、それ以外は、積分計算は必要ありません。
楕円弦長さは、楕円と、指定された角度の直線と楕円の交点の座標から長さをけいさんします。
扇面積は、上記交点のY座票を円の座標に変換し、円上の角度を計算、その角度から円上の扇部の面積を計算し、更に楕円比b/aで変換して、楕円上の扇面積とします。
三角面積は、円上の角度と半径aの二等辺三角形の面積を計算、これも楕円比で変換して、楕円上の三角部の面積とします。
楕円弧面積は、計算範囲の角度が180°より小さい場合は、扇面積から、三角面積を減算し、大きい場合は加算すれば得ることが出来ます。
プログラム
楕円積分には、カールソンの第二種楕円積分を使用しています。
楕円弦長さは、楕円積分用に、円上の角度に変更してから、楕円上の座標を計算して求めています。
(楕円と、傾き角θの直線の交点を求めている時に計算しても良いのですが、計算の都合上、積分用角度から計算しています。)
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Image1: TImage;
Panel1: TPanel;
arEdit: TLabeledEdit;
brEdit: TLabeledEdit;
sttEdit: TLabeledEdit;
endEdit: TLabeledEdit;
Button1: TButton;
procedure FormCreate(Sender: TObject);
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
procedure ImageClear;
function draw_ellipse: boolean;
function EllipseInput(var ar, br, sttQ, endQ: double): boolean;
procedure ellipse_calc(ar, br, q, magnification: double; var x, y: double);
procedure Linedlaw(x1, y1, x2, y2: double; Xsift, Ysift: integer; LF: boolean);
procedure divisionpartition;
function second_imperfect_elliptic_integral(QD, K: double): double;
procedure elliptic_integral;
function circle_calc(ar, br, q: double): double;
procedure elliptical_arc_area;
function RF(x1, y1, z1: Extended): Extended;
function RJ(x1, y1, z1, p1: Extended): Extended;
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses System.Math;
//-----------------------------
// 表示画像消去
//-----------------------------
procedure TForm1.ImageClear;
begin
image1.Canvas.Brush.Style := bsSolid;
image1.Canvas.Brush.Color := clWhite;
image1.Canvas.FillRect(Rect(0, 0, image1.Width, image1.Height));
end;
//--------------------------
// 2点間線引き
//--------------------------
procedure TForm1.Linedlaw(x1, y1, x2, y2: double; Xsift, Ysift: Integer; LF: boolean);
var
xp1, yp1, xp2, yp2: integer;
begin
if LF then begin
xp1 := round(x1) + Xsift;
yp1 := image1.Height - round(y1) - Ysift;
image1.Canvas.MoveTo(xp1, yp1);
end;
xp2 := round(x2) + Xsift;
yp2 := image1.Height - round(y2) - Ysift;
image1.Canvas.LineTo(xp2, yp2);
end;
//-------------------------------------------------------------
// 楕円上の座標計算
// q 角度
// ar , br 半径
// magnification 倍率
// x, y 座標
// q 角度は中心に対するxy座標の角度ではないので注意が必要です。
//-------------------------------------------------------------
procedure TForm1.ellipse_calc(ar, br, q, magnification: double; var x, y: double);
begin
x := ar * cos(q) * magnification;
y := br * sin(q) * magnification;
end;
//-----------------------
// 楕円作図
//-----------------------
function TForm1.draw_ellipse: boolean;
const
divideN = 2000; // 作図用分割数
draw_margin = 100; // 作図余白
var
ar, br : double;
sttQ, endQ : double;
stBQ, enBQ : double;
maxr : double;
I : integer;
dq : double;
x1, y1 : double;
x2, y2 : double;
Xsift, Ysift : integer;
magnification : double;
sttN, endN : integer;
// x1,y1-x2,y2 線引き
procedure DlawCalc;
begin
ellipse_calc(ar, br, dq * I, magnification, x2, y2);
if I = sttN + 1 then Linedlaw(x1, y1, x2, y2, Xsift, Ysift, True)
else Linedlaw(x1, y1, x2, y2, Xsift, Ysift, False);
x1 := x2;
y1 := y2;
end;
begin
result := True;
if not EllipseInput(ar, br, sttQ, endQ) then begin
result := False;
exit;
end;
// 開始角と終了角が等しかったら全周とします。
stBQ := sttQ / 180 * pi;
enBQ := endQ / 180 * pi;
if sttQ = endQ then begin
sttQ := 0;
endQ := 360;
end;
// 画像消去
ImageClear;
// 作図設定
Xsift := image1.Width div 2;
Ysift := image1.Height div 2 + 30;
sttQ := sttQ / 180 * pi;
endQ := endQ / 180 * pi;
// 作図計算ピッチ計算
dq := 2 * pi / divideN;
// 大きい方の半径選択
maxr := ar;
if br > ar then maxr := br;
// 作図倍率設定
magnification := (Xsift - draw_margin) / maxr;
// 楕円作図
image1.Canvas.Pen.Style := psSolid;
image1.Canvas.Pen.Color := clBlue;
image1.Canvas.Pen.Width := 1;
sttN := 0;
// 最初の角度
ellipse_calc(ar, br, 0, magnification, x1, y1);
// 最後まで
for I := 1 to divideN do DlawCalc;
// 楕円弧作図
image1.Canvas.Pen.Color := clRed;
image1.Canvas.Pen.Width := 4;
sttN := trunc(stBQ / dq);
endN := trunc(enBQ / dq);
// 最初の角度
ellipse_calc(ar, br, stBQ, magnification, x1, y1);
// 開始角より終了角が大きい場合
if endQ > sttQ then begin
ellipse_calc(ar, br, sttN * dq, magnification, x1, y1);
for I := sttN + 1 to endN do DlawCalc;
end
// 開始角より終了角が小さい場合
else begin
// 開始角より360°迄作図
for I := sttN + 1 to divideN do DlawCalc;
// 0°(=360°)から終了角迄作図
for I := 1 to endN do DlawCalc;
end;
// 最後の角度
ellipse_calc(ar, br, enBQ, magnification, x2, y2);
Linedlaw(x1, y1, x2, y2, Xsift, Ysift, True);
// 楕円弦作図
// 最後の角度
ellipse_calc(ar, br, enBQ, magnification, x2, y2);
// 最初の角度
ellipse_calc(ar, br, stBQ, magnification, x1, y1);
image1.Canvas.Pen.Color := clGreen;
image1.Canvas.Pen.Width := 2;
Linedlaw(x1, y1, x2, y2, Xsift, Ysift, true);
// 扇線作図
image1.Canvas.Pen.Color := clMaroon;
image1.Canvas.Pen.Width := 2;
Linedlaw(X1, Y1, 0, 0, Xsift, Ysift, true);
Linedlaw(0, 0, X2, Y2, Xsift, Ysift, true);
// 中心線作図
image1.Canvas.Pen.Width := 1;
image1.Canvas.Pen.Style := psDashDot;
image1.Canvas.Pen.Color := clGreen;
Linedlaw(-50, 0, 50, 0, Xsift, Ysift, True);
Linedlaw( 0, -50, 0, 50, Xsift, Ysift, True);
end;
//-------------------------------------------------------------
// 円変換時の 角度計算
// 積分角度 q 角度
// ar , br 半径
// x^2/a^2 + y^2/b^2 = 1 と 角度θの直線y = cx の連立方程式の
// の解法による円変換時の角度の計算
//-------------------------------------------------------------
function TForm1.circle_calc(ar, br, q: double): double;
var
c, ga, sq, cb: double;
x, y : double;
begin
if (q = 0) or (q = 90) or (q = 180) or (q = 270) or (q = 360) then begin
result := q;
exit;
end;
// 楕円と直線の交点の計算
sq := pi / 180 * q;
c := tan(sq); // y = cx 傾斜c計算
cb := c * c / br / br; // y^2/b^2 のyに代入
ga := 1 / ar / ar; //
x := sqrt(1 / (ga + cb)); // xの値
// xの値がプラスしか計算されないので角度により符号設定
if (q > 90) and (q < 270) then x := - x;
y := c * x * ar / br; // 円上のyの値
// xy座標円中心角度に変換
result := arctan2(y, x) / pi * 180;
// -角度は時はプラスに修正
if result < 0 then result := result + 360;
end;
//--------------------
// 楕円の値入力処理
//--------------------
function TForm1.EllipseInput(var ar, br, sttQ, endQ: double): boolean;
var
ch : integer;
begin
result := false;
val(arEdit.Text, ar, ch);
if ch <> 0 then begin
application.MessageBox('半径aは数値ではありません。', '半径a', 0);
exit;
end;
if ar <= 0 then begin
application.MessageBox('半径aがゼロ 又はゼロ以下です。', '半径a', 0);
exit;
end;
val(brEdit.Text, br, ch);
if ch <> 0 then begin
application.MessageBox('半径bは数値ではありません。', '半径b', 0);
exit;
end;
if br < 0 then begin
application.MessageBox('半径bがゼロ 又はゼロ以下です。', '半径b', 0);
exit;
end;
val(sttEdit.Text, sttQ, ch);
if ch <> 0 then begin
application.MessageBox('開始角は数値ではありません。', '開始角', 0);
exit;
end;
val(endEdit.Text, endQ, ch);
if ch <> 0 then begin
application.MessageBox('終了角は数値ではありません。', '終了角', 0);
exit;
end;
// 角度が0~360°の範囲に無かったら修正
Repeat
if sttQ > 360 then sttQ := sttQ - 360;
if sttQ < 0 then sttQ := SttQ + 360;
if endQ > 360 then endQ := endQ - 360;
if endQ < 0 then endQ := endQ + 360;
Until (sttQ >= 0) and (sttQ <= 360) and (endQ >= 0) and (endQ <= 360);
// 入力角度に長径を基準とした角度θをを使用しています。
// 楕円積分は短径を基準にsinαで表される距離に対する積分となります。
// 入力された角度をそのまま使用する事は出来ません。
// 楕円の中心位置を通る直線 y=cx の cを c= tanθ として楕円との交点を求め
// 交点yの値を円変換時の値y'=y*a/bに変換、φ=arctan2(y',x)として
// 円上の角度に変換して、x=cos(φ)*a y=sin(φ)*b θ=arctan(x,y)のθが入力値と
// 一致するようにします。
// 楕円積分時は更に、長径基準φを短径基準αに変換して計算します。
sttQ := circle_calc(ar, br, sttQ);
endQ := circle_calc(ar, br, endQ);
if sttQ = 360 then sttQ := 0;
result := true;
end;
//---------------------------------
// 周長 楕円弧長の分割計算
//---------------------------------
procedure TForm1.divisionpartition;
const
divideN = 1440000; // 全周計算分割数
divide4 = 4000; // 指定範囲分割数基礎数
PI2 = 2 * pi; // 2π
K180 = 180; // 180°
K360 = 360; // 360°
var
ar, br : double; // 半径a , b
sttQ, endQ : double; // 積分開始角、積分終了角 deg単位
I : integer; //
dq : double; // 微小角Δq
x1, y1 : double; // 始点座標
x2, y2 : double; // 終点座標
sttN : integer; // 分割数
Lng, All : double; // 楕円弧長 周長
Q : double; // 座標計算角度
basQ, topQ : double; // 積分開始角、積分終了角 rad単位
// 座標の計算と微小角に対する距離の計算と加算
procedure LngCalc;
var
xh2, yh2 : double;
begin
Q := basQ + dq * I; // 座標計算角度
if Q >= PI2 then Q := Q - PI2;
ellipse_calc(ar, br, Q, 1, x2, y2); // 座標計算
xh2 := x2 - x1;
yh2 := y2 - y1;
Lng := Lng + sqrt(xh2 * xh2 + yh2 * yh2);
x1 := x2;
y1 := y2;
end;
begin
// 各値の入力値変換
if not EllipseInput(ar, br, sttQ, endQ) then exit;
// 全周計算ピッチ計算
dq := PI2 / divideN;
Lng := 0;
// 全周長計算
ellipse_calc(ar, br, 0, 1, x1, y1);
for I := 1 to divideN do LngCalc;
All := Lng; // 全周長
// 指定範囲計算
basQ := sttQ / K180 * pi;
topQ := endQ / K180 * pi;
// 分割数と微小角度Δqの計算
if endQ >= sttQ then begin
sttN := round((endQ - sttq) * divide4); // 分割数
if sttN = 0 then sttN := 1; // ゼロでの除算防止
dq := (topQ - basQ) / sttN; // Δq
end
else begin
sttN := round((endQ + K360 - sttQ) * divide4); // 分割数
if sttN = 0 then sttN := 1; // ゼロでの除算防止
dq := (topQ + PI2 - basQ) / sttN; // Δq
end;
Lng := 0;
// 最初の座標
ellipse_calc(ar, br, basQ, 1, x1, y1);
for I := 1 to sttN do begin
LngCalc;
end;
Image1.Canvas.TextOut(20, 2,'微小角分割積分 楕円弧長= ' + floatTostr(Lng));
Image1.Canvas.TextOut(20,17,'微小角分割積分 周 長 = ' + floatTostr(ALL));
end;
// Carlson's Elliptic Integral RJ
function TForm1.RJ(x1, y1, z1, p1: Extended): Extended;
var
s, fa, rj, rk : Extended;
la, mu : Extended;
al, be : Extended;
r1, a1, b1 : Extended;
a2, b2, mv, s1 : Extended;
rc, r0 : Extended;
s12, s13, s14 : Extended;
s15, s16 : Extended;
x2, y2, z2 : Extended;
x3, y3, z3 : Extended;
s2, s3, p2, p3 : Extended;
s4, s5 : Extended;
x31, y31, z31, p31 : Extended;
s22, s23, s2s3 : Extended;
procedure rcab;
begin
rc := 1;
a1 := al;
b1 := be;
repeat
r1 := rc;
la := 2 * sqrt(a1 * b1) + b1;
a2 := (a1 + la) / 4;
b2 := (b1 + la) / 4;
mv := (a1 + 2 * b1) / 3;
s1 := (b1 - a1) / (3 * mv);
s12 := s1 * s1;
s13 := s12 * s1;
s14 := s13 * s1;
s15 := s14 * s1;
s16 := s15 * s1;
rc := (1 + 3 * s12 / 10 + s13 / 7 + 3 * s14 / 8 + 9 * s15 / 22 + 159 * s16 / 208) / sqrt(mv);
a1 := a2;
b1 := b2;
until r1 = rc;
end;
function ss: Extended;
begin
x31 := x31 * x3;
y31 := y31 * y3;
z31 := z31 * z3;
p31 := p31 * p3;
result := (x31 + y31 + z31 + p31);
end;
begin
s := 0;
fa := 3;
rj := 0;
repeat
r0 := rj;
la := sqrt(x1 * y1) + sqrt(x1 * z1) + sqrt(y1 * z1);
mu := (x1 + y1 + z1 + 2 * p1) / 5;
x2 := (x1 + la) / 4;
y2 := (y1 + la) / 4;
z2 := (z1 + la) / 4;
p2 := (p1 + la) / 4;
x3 := 1 - x1 / mu;
y3 := 1 - y1 / mu;
z3 := 1 - z1 / mu;
p3 := 1 - p1 / mu;
x31 := x3;
y31 := y3;
z31 := z3;
p31 := 2 * p3;
s2 := ss / 4;
s3 := ss / 6;
s4 := ss / 8;
s5 := ss / 10;
al := (sqrt(x1) + sqrt(y1) + sqrt(z1)) * p1 + sqrt(x1 * y1 * z1);
al := al * al;
be := p1 * (p1 + la) * (p1 + la);
rcab;
s22 := 3 * s2 * s2 / 22;
s23 := s2 * s2 * s2 / 10;
s2s3 := s2 * s3 * 3 / 13;
s := s + fa * rc;
rk := 1 + 3 * s2 / 7 + s3 / 3 + s22 + s2s3 + 3 * s4 / 11 + 3 * s5 / 13 - s23;
fa := fa / 4;
mu := sqrt(1 / (mu * mu * mu));
rj := s + fa / 4 * (rk + 3 * s3 * s3 / 10 + 3 * s2 * s4 / 5) * mu;
x1 := x2;
y1 := y2;
z1 := z2;
p1 := p2;
until rj = r0;
result := rj;
end;
// Carlson's Elliptic Integral RF
function TForm1.RF(x1, y1, z1: Extended): Extended;
var
la, mu : Extended;
x2, y2, z2 : Extended;
x3, y3, z3 : Extended;
s2, s3 : Extended;
r0, rf : Extended;
s22, s23, s2s3, s32 : Extended;
begin
rf := 0;
repeat
r0 := rf;
la := sqrt(x1 * Y1) + sqrt(x1 * z1) + sqrt(y1 * z1);
mu := (x1 + y1 + z1) / 3;
x2 := (x1 + la) / 4;
y2 := (y1 + la) / 4;
z2 := (z1 + la) / 4;
x3 := 1 - x2 / mu;
y3 := 1 - y2 / mu;
z3 := 1 - z2 / mu;
s2 := (x3 * x3 + y3 * y3 + z3 * z3) / 4;
s3 := (x3 * x3 * x3 + y3 * y3 * y3 + z3 * z3 * z3) / 6;
s22 := s2 * s2 / 6;
s23 := 5 * s2 * s2 * s2 / 26;
s32 := 3 * s3 * s3 / 26;
s2s3 := s2 * s3 * 3 / 11;
rf := (1 + s2 / 5 + s3 / 7 + s22 + s2s3 + s23 + s32) / sqrt(mu);
x1 := x2;
y1 := y2;
z1 := z2;
until rf = r0;
result := rf;
end;
// 第二種楕円積分 --------------------------------------------------
function TForm1.second_imperfect_elliptic_integral(QD, K: double): double;
var
s, s2, s3 : double;
c2 : double;
rf0, rd0 : double;
k2 : double;
eqk, eqk90 : double;
eqd, eek : double;
eq : double;
J : integer;
begin
J := trunc(ABS(QD) / 90);
if J mod 2 <> 0 then // 第2,第4象限の積分角度
eqd := (J + 1) * 90 - ABS(QD)
else // 第1,第3象限の積分角度
eqd := ABS(QD) - (90 * J);
eq := eqd / 180 * pi;
K2 := K * K;
eqk90 := 0;
if J > 0 then begin // 積分範囲90度より大きかったら
if K = 1 then eqk90 := 1 // k=1 だったら 90°の積分値は1
else begin // K<1の時 90°の積分値計算
rf0 := RF(0, 1 - k2, 1);
rd0 := RJ(0, 1 - k2, 1, 1);
eqk90 := rf0 - k2 / 3 * rd0; // rf0 - k^2 / 3 * RD
end;
end;
if (eqd < 90) or (K < 1) then begin
if K < 1 Then begin
c2 := cos(eq) * cos(eq);
s := sin(eq);
s2 := s * s;
s3 := s2 * s;
rf0 := RF(c2, 1 - k2 * s2, 1);
rd0 := RJ(c2, 1 - k2 * s2, 1, 1);
eek := s * rf0 - k2 / 3 * s3 * rd0;
end
else eek := sin(eq);
end
else eek := 1;
if j mod 2 <> 0 then begin // 第2,第4象限の積分値
eqk := (J + 1) * eqk90 - eek;
end
else begin // 第1,第3象限の積分値
eqk := J * eqk90 + eek;
end;
if QD < 0 then eqk := - eqk;
result := eqk;
end;
//--------------------------------------------------
// 楕円積分による周長計算
// カールソンによる計算をしていますが90°までしか
// 計算出来ないので90°に分けて計算しています。
// 楕円積分は短径が基準となっていますが、角度は長径が
// 基準となっているので楕円弧長計算時変換しています。
//--------------------------------------------------
procedure TForm1.elliptic_integral;
var
ar, br : double;
sttQ, endQ : double;
K, A, L : double;
sttL, endL : double;
IND : integer;
// 角度、象限による楕円弧長計算
function Elliptical_arc(q : double; I: integer): double;
var
sttendR : double;
begin
result := 0;
case I of
0, 2 : begin // 第一、三象限
sttendR := (I + 1) * 90 - q;
result := (I + 1) * A - ar * second_imperfect_elliptic_integral(sttendR, K);
end;
1, 3 : begin // 第二、四象限
sttendR := q - (90 * I);
result := I * A + ar * second_imperfect_elliptic_integral(sttendR, K);
end;
end;
end;
begin
// 各値の入力値変換
if not EllipseInput(ar, br, sttQ, endQ) then exit;
// 半径Brの方が大きかったら入れ替え 角度を90°変更
if br > ar then begin
k := ar;
ar := br;
br := k;
if (sttQ <> 0) or (endQ <> 360) then begin
sttQ := sttQ + 90;
endQ := endQ + 90;
if sttQ >= 360 then sttQ := sttQ - 360;
if endQ > 360 then endQ := endQ - 360;
end;
end;
sttL := 0;
endL := 0;
K := sqrt(1 - br * br / ar / ar); // k 離心率
// double時のKの値の誤差対策
if 1 - K < 1E-15 then K := 1;
// 角度90°楕円弧長計算
A := ar * second_imperfect_elliptic_integral(90, K); // 半径 x 第2種楕円積分
// 範囲計算 象限による計算
for IND := 3 downto 0 do begin
// 開始楕円弧長計算
if (IND * 90 <= sttQ) and (sttQ < (IND + 1) * 90) then
sttL := Elliptical_arc(sttQ, IND);
// 終了楕円弧長計算
if (IND * 90 < endQ) and (endQ <= (IND + 1) * 90) then
endL := Elliptical_arc(endQ, IND);
end;
// 開始角と終了角の大きさで計算方法変更
if endQ >= sttQ then L := endL - sttL
else L := 4 * A - sttL + endL;
Image1.Canvas.TextOut(20, image1.Height - 32,'楕円積分 楕円弧長= ' + floatTostr(L));
Image1.Canvas.TextOut(20, image1.Height - 17,'楕円積分 周 長 = ' + floatTostr(4 * A));
end;
// 楕円弧部、扇部、楕円弦長等計算
procedure TForm1.elliptical_arc_area;
var
ar, br : double;
sttQ, endQ : double;
x1, y1, x2, y2 : double;
L, Sc, Sa, St : double;
begin
// 各値の入力値変換
if not EllipseInput(ar, br, sttQ, endQ) then exit;
// 楕円弦長さ計算
x1 := cos(sttQ / 180 * pi) * ar;
y1 := sin(sttQ / 180 * pi) * br;
x2 := cos(endQ / 180 * pi) * ar;
y2 := sin(endQ / 180 * pi) * br;
L := sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
Image1.Canvas.TextOut(20, image1.Height - 47,'楕円弦長= ' + floatTostr(L));
// 半径Rの円の面積
Sc := pi * ar * ar;
// 扇部面積
if endQ >= sttQ then
Sa := Sc * (endQ - sttq) / 360
else
Sa := SC * (360 + endQ - sttq) / 360;
Sa := Sa * br / ar;
Image1.Canvas.TextOut(20, image1.Height - 62,'扇部面積= ' + floatTostr(Sa));
// 三角形部面積
if endQ >= sttQ then begin
St := ar * sin((endQ - sttq) / 180 * pi) / 2 * br; // ar^2 * sin(θ) / 2 * br / ar
end
else begin
St := ar * sin((360 + endQ - sttq) / 180 * pi) / 2 * br;
end;
Image1.Canvas.TextOut(20, image1.Height - 77,'三角部面積= ' + floatTostr(abs(St)));
Image1.Canvas.TextOut(20, image1.Height - 92,'楕円弧部面積= ' + floatTostr(Sa - St));
Image1.Canvas.TextOut(20, image1.Height - 107,'楕円面積= ' + floatTostr(ar * br * pi));
// 形状図形線色表示
image1.Canvas.Pen.Style := psSolid;
image1.Canvas.Pen.Width := 4;
// 楕円弧長
image1.Canvas.Pen.Color := clRed;
image1.Canvas.MoveTo(270, image1.Height - 25);
image1.Canvas.LineTo(300, image1.Height - 25);
// 楕円弦長
image1.Canvas.Pen.Color := clGreen;
image1.Canvas.MoveTo(270, image1.Height - 40);
image1.Canvas.LineTo(300, image1.Height - 40);
// 扇部面積
image1.Canvas.Pen.Color := clMaroon;
image1.Canvas.MoveTo(270, image1.Height - 55);
image1.Canvas.LineTo(300, image1.Height - 55);
image1.Canvas.MoveTo(330, image1.Height - 55);
image1.Canvas.LineTo(360, image1.Height - 55);
image1.Canvas.Pen.Color := clRed;
image1.Canvas.MoveTo(300, image1.Height - 55);
image1.Canvas.LineTo(330, image1.Height - 55);
// 三角部面積
image1.Canvas.Pen.Color := clMaroon;
image1.Canvas.MoveTo(270, image1.Height - 70);
image1.Canvas.LineTo(300, image1.Height - 70);
image1.Canvas.MoveTo(330, image1.Height - 70);
image1.Canvas.LineTo(360, image1.Height - 70);
image1.Canvas.Pen.Color := clGreen;
image1.Canvas.MoveTo(300, image1.Height - 70);
image1.Canvas.LineTo(330, image1.Height - 70);
// 楕円弧部面積
image1.Canvas.Pen.Color := clRed;
image1.Canvas.MoveTo(270, image1.Height - 85);
image1.Canvas.LineTo(300, image1.Height - 85);
image1.Canvas.Pen.Color := clGreen;
image1.Canvas.MoveTo(300, image1.Height - 85);
image1.Canvas.LineTo(330, image1.Height - 85);
end;
//----------------------
// 周長 楕円弧長計算
//----------------------
procedure TForm1.Button1Click(Sender: TObject);
begin
if not draw_ellipse then exit; // 作図
divisionpartition; // 分割計算
elliptic_integral; // 不完全楕円積分計算
elliptical_arc_area;
end;
//------------
// 初期設定
//------------
procedure TForm1.FormCreate(Sender: TObject);
begin
ClientHeight := 479;
ClientWidth := 639;
Image1.Top := 0;
Image1.Left := 0;
Image1.Height := ClientHeight;
Image1.Width := ClientHeight;
Image1.Canvas.Font.Height := 15;
Panel1.Top := 8;
Panel1.Left := 502;
Panel1.Height := 313;
Panel1.Width := 113;
end;
end.
 EllipsePerimeterNo3.zip
EllipsePerimeterNo3.zip
各種プログラム計算例に戻る
最初に戻る
 楕円に対して、指定された角度の範囲に対して、楕円弧長さ、楕円弧面積、楕円弦長さ、楕円扇面積の計算をします。
楕円に対して、指定された角度の範囲に対して、楕円弧長さ、楕円弧面積、楕円弦長さ、楕円扇面積の計算をします。