2020/01/06
多倍長ルーチンの離心率(k)の値の後ろに"i"の文字を付けることで離心率(k)の虚数の入力を可能にしました。
楕円の半径aと半径bの入力により計算可能にしました。
2020/12/27
多倍長楕円積分の.ルーチンを整理したものにしました。
2020/12/12
多倍長楕円積分の値が∞に成る時、積分方向がマイナスなら-∞になる様に修正しました。
2020/02/10
楕円積分計算のｋ２の代わりにパラメーターｍを使用するように計算を変更しました。
2020/01/06
90°分割計算の第二種楕円積分でK=1の時計算出来なかったのを修正しました。
2019/12/20
ルジャンドルの積分計算の場合
離芯率ｋの値が１を超えても、積分範囲は狭くなるが積分可能であることに対処しました。
(多倍長の計算プログラムのみ修正しました。)
2019/11/14
第一、二、三同時積分プログラムのDouble精度の角度マイナス側の符号設定もれ修正
2018/07/05
第二種積分 一部８バイト演算桁落ち対策(Kの値が１に近いときの判別)
2018/06/03
第一、二種楕円積分追加
第一、二、三種楕円積分
楕円積分の中に第三種楕円積分があります。
第一種、第二種楕円積分は、楕円体の表面積や、楕円の周長計算、振り子の周期計算等に利用されていますが、第三種楕円積分の利用例はあまり見かけません。
しかし、楕円積分の一つとして、必ず取り上げられていので、Delphiでプログラムを組んでみました。
元のプログラムは、インターネットで探し、Delphi用に組みなおしています。
プログラムは計算式のｋ２をパラメータｍに置き換えています。
離心率は ｋ＝√（(ａ２－ｂ２）／ａ２）で、ａ が長径で、ｂ が短径としないと、離心率 ｋ
の値が虚数となりますが。
パラメーター ｍ＝（ａ２－ｂ２）／ａ２ として計算すれば、 ａ の値より ｂ の値が大きくても、 ｍ の値がマイナスになるだけで、積分が可能です。
ｋ＝√（(ａ２－ｂ２）／ａ２）
ｍ＝ｋ２
ｍ＝（ａ２－ｂ２）／ａ２
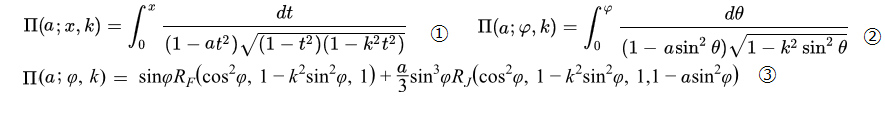
上記の公式の最後の式３が実際にプログラムをしたカールソンの計算式です。
プログラムは、8バイトの精度と、多倍長の精度で組んであります。
上記式では、分母がゼロに近づくと、値が非常に大きくなるため、計算精度が悪くなり8バイトの演算と、多倍長演算では計算結果に大きな差がでます。
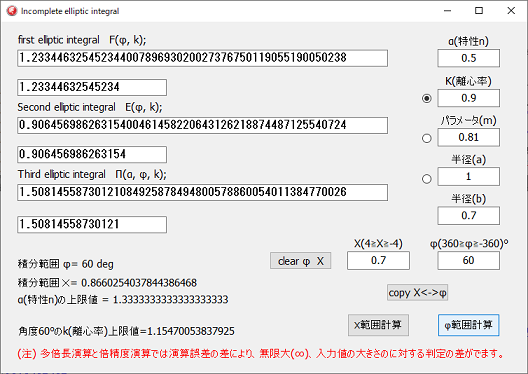k=√(1-b2/a2) 離心率 a 長半径 b 短半径
上記式１の場合は、 x=sin(φ) (積分範囲
１～－１) φ=sin-1x となり積分範囲が
90°(π/2)～-90°(-π/2)を超える事はありません。
α (特性n)の値の範囲は、積分の範囲 φ によって変動します。
特性nのnは、αではなく、n で表している公式があるので、併記しているだけです。
αsin2φ
の値が1になると、無限大になってしまい計算が出来ません。
k2sin2φ の値が1になると、同じ様に無限大になります。上図の式の上側右の式 ２の場合、α と k の値が
1 以下であれば、積分角度の上限はありませんので他 の公式と完全に同じではありません。
積分の範囲 π/2～-π/2 に関してのみ等しくなります。
又、αsin2φ、k2sin2φが１以下であれば、α と k の値が
１を超えても、積分の上限値が小さくなるだけで積分可能です。
３の式の場合は90°までしか計算できないので、90°以上の場合、90°単位に分割して、計算するようにプログラムを組みました。
プログラム上、積分の範囲に上限はないのですが、一応 ±360°迄にしました。
計算はカールソンの楕円積分計算なので、簡単に、第一種、第二種楕円積分も出来るので、プログラムに追加しました。
第一種楕円積分は、第二種、第三種楕円積分に含まれているので、必然的に計算がされます。
パラメーターｍのラジオボタンにチェックを入れれば、パラメーターｍの値が採用されます。
半径のラジオボタンにチェックを入れれば、楕円の半径を元に計算されます。
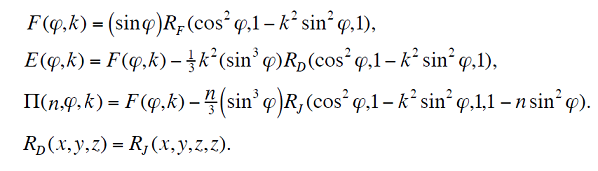
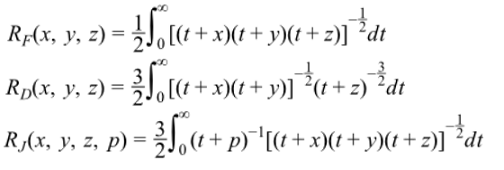
微小角分割積分計算
プログラムの確認の為、微小分割積分のプログラムを先に検討しました。
ルジャンドルの標準型 第三種楕円積分は一番上の式２です。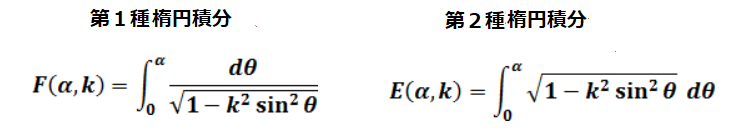
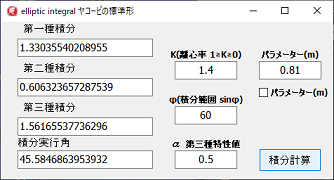微小角分割方式なので、90°象限のルーチンは使用していません。
第一種、第二種の答えの表示も出る様にしました。
分母の値が小さくなると、計算上 誤差が大きくなります。
第一種、第二種の場合、K(離心率)の値が１を超えなければ、積分範囲の上限はありません。
ルジャンドルの標準型で第二種の場合は、Kが１でも、積分の範囲に上限無しです。
第三種の場合、α(特性値)と、K(離心率)の値の両方が１を超えなければ、積分範囲の上限は無しです。
ルジャンドルの標準型で、α=0. k= 0 でπ(180°) 迄積分すると、全て
π になります。
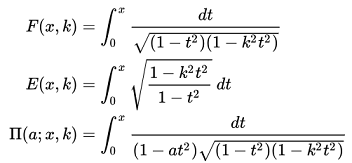左の式は、ヤコービの標準形ですが、単にt=sin(φ)として、ルジャンドルの式と同じ扱いをしている場合もありますが、ヤコービの標準形の場合、α(特性値)、K(離心率)が１以下であっても、積分の範囲がX=１=sin(φ)を超えることは出来ません。
ヤコービの式と、ルジャンドルの式を＝で結ぶ場合は、積分の範囲 φ を π/2 迄に限定する必要があります。
微小角分割プログラム (ルジャンドルの式)
積分の範囲角度(φ)には制限がありませんが、一応360°迄にしています。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
Edit1: TEdit;
Label1: TLabel;
Label2: TLabel;
Edit2: TEdit;
LabeledEdit3: TLabeledEdit;
Edit3: TEdit;
Label3: TLabel;
CheckBox1: TCheckBox;
LabeledEdit4: TLabeledEdit;
LabeledEdit5: TLabeledEdit;
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
procedure Elliptic;
function Datainput(var m, Q, A: Extended): boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
function TForm1.Datainput(var m, Q, A: Extended): boolean;
var
Ch: integer;
k : Extended;
begin
// k := 0;
Result := False;
if not checkbox1.Checked then begin
val(LabeledEdit1.Text, K, CH);
if Ch <> 0 then begin
application.MessageBox('離心率(k)が数値ではありません。','K(離心率)', 0);
exit;
end;
m := k * k;
end
else begin
val(LabeledEdit4.Text, m, CH);
if Ch <> 0 then begin
application.MessageBox('パラメーター(m)が数値ではありません。','m(パラメーター)', 0);
exit;
end;
// if m > 0 then k := sqrt(m);
end;
// if abs(K) > 1 then begin
// application.MessageBox('離心率(k)が範囲外です。','K(離心率)', 0);
// exit;
// end;
val(LabeledEdit2.Text, Q, CH);
if Ch <> 0 then begin
application.MessageBox('積分の範囲が数値ではありません。','φ(積分範囲)', 0);
exit;
end;
if abs(Q) > 360 then begin
application.MessageBox('積分の範囲abs(X)が大きすぎます','φ(積分範囲)', 0);
exit;
end;
val(LabeledEdit3.Text, A, CH);
if Ch <> 0 then begin
application.MessageBox('第三種αの値が数値ではありません。','第三種 α', 0);
exit;
end;
Result := True;
end;
// 積分計算はルジャンドルの標準形
procedure TForm1.Elliptic;
const
N = 4000000;
var
i, J : integer;
Q, st : Extended;
m, t, t2 : Extended;
Pq, dq : Extended;
Fxk : Extended;
Exk : Extended;
Fxka : Extended;
S1, S2 : Extended;
a, t3 : Extended;
LA, LB : Extended;
ms : Extended;
ps2 : Extended;
begin
if not Datainput(m, Q, a) then exit;
ps2 := pi / 2;
Pq := Q / 180 * pi;
J := abs(round(Pq * N)); // Q(積分範囲)が非常に小さい場合 J(分割数)がゼロになるので
if J = 0 then Q := 0; // その時は、Q=0とします。
if Q = 0 then begin
Edit1.Text := '0';
Edit2.Text := '0';
Edit3.Text := '0';
Edit3.Text := '0';
exit;
end;
dq := Pq / J;
Exk := 0;
Fxk := 0;
Fxka := 0;
ms := 0.5; // 計算中間点
for I := 0 to J - 1 do begin // 積分の範囲のは ms * dx から X - dx * ms 迄です。
t := (I + ms) * dq; // 中間値で計算し計算精度をあげます。
st := sin(t); // sinθ
t2 := st * st; // sin^2θ
t3 := t2 * m; // k^2*sin^2θ
S1 := (1 - t3); // 1-k^2*sin^2θ
if S1 < 0 then break;
S2 := (1 - a * t2); // 1-a*sin^2θ
LA := sqrt(S1); // √(1-k^2*sin^2θ)
Exk := Exk + LA * dq; // 第二種楕円積分
LB := S2 * LA; // (1-a*sin^2θ) * √(1-k^2*sin^2θ)
if (m < 1) or (abs(Pq) < ps2) then begin // (K < 1) or (θ < 90°)
Fxk := Fxk + dq / LA; // 第一種楕円積分
if LB > 0 then Fxka := Fxka + dq / LB; // 第三種楕円積分
end;
end;
q := (t - dq) / pi * 180;
labelededit5.Text := floatTostr(q);
if (m = 1) and (abs(Pq) >= ps2) then begin // 第一種楕円積分答え
Edit1.Text := '∞';
end
else Edit1.Text := floattostr(Fxk);
Edit2.Text := floattostr(Exk); // 第二種楕円積分答え
Edit3.Text := floattostr(Fxka); // 第三種楕円積分答え
if (abs(pq) >= ps2) then begin // θ >= 90°
if (m = 1) or (a = 1) then Edit3.Text := '∞';
if (a > 1) then Edit3.Text :='αの値が大きすぎます。';
end
else begin // θ < 90°
S2 := sin(pq) * sin(pq) * a; // a * sin^2(θ)
if (S2 > 1) then Edit3.Text := 'αの値が大きすぎます。';
if (S2 = 1) then Edit3.Text := '∞'; // 演算誤差により発生率低い
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
Elliptic;
end;
end.
微小角分割プログラム (ヤコービの式)
積分範囲の値が角度となっていますが、計算時 積分範囲 X=sin(φ) としてしていますので１を超えることはありません。
sin(100°)はsin(80°)=0.9848と同じです。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
Edit1: TEdit;
Label1: TLabel;
Label2: TLabel;
Edit2: TEdit;
LabeledEdit3: TLabeledEdit;
Edit3: TEdit;
Label3: TLabel;
LabeledEdit4: TLabeledEdit;
CheckBox1: TCheckBox;
LabeledEdit5: TLabeledEdit;
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
procedure Elliptic;
function Datainput(var m, X, A: Extended): boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
function TForm1.Datainput(var m, X, A: Extended): boolean;
var
Ch: integer;
Q, k: extended;
begin
Result := False;
// k := 0;
if not checkbox1.Checked then begin
val(LabeledEdit1.Text, K, CH);
if Ch <> 0 then begin
application.MessageBox('離心率(k)が数値ではありません。','K(離心率)', 0);
exit;
end;
m := k * k;
end
else begin
val(LabeledEdit4.Text, m, CH);
if Ch <> 0 then begin
application.MessageBox('パラメーター(m)が数値ではありません。','K(離心率)', 0);
exit;
end;
// if m > 0 then k := sqrt(m);
end;
// if (K > 1) or (K < -1) then begin
// application.MessageBox('離心率が範囲外です。','K(離心率)', 0);
// exit;
// end;
val(LabeledEdit2.Text, Q, CH);
if Ch <> 0 then begin
application.MessageBox('積分の範囲が数値ではありません。','X(積分範囲)', 0);
exit;
end;
X := sin(Q / 180 * pi);
val(LabeledEdit3.Text, A, CH);
if Ch <> 0 then begin
application.MessageBox('第三種αの値が数値ではありません。','第三種 α', 0);
exit;
end;
Result := True;
end;
// 積分計算はヤコービの標準形
procedure TForm1.Elliptic;
const
N = 10000000;
var
i, J : integer;
X : Extended;
m, t2 : Extended;
t, dx : Extended;
Fxk : Extended;
Exk : Extended;
Fxka : Extended;
S1, S2 : Extended;
S3, A1 : Extended;
LA, LB : Extended;
ms : Extended;
begin
if not Datainput(m, X, A1) then exit;
t := 0;
dx := 1 / N;
J := Round(abs(X) / dx); // X(積分範囲)が非常に小さい場合 J(分割数)がゼロになるので
if J = 0 then X := 0; // その時は、X=0とします。
if X = 0 then begin
Edit1.Text := '0';
Edit2.Text := '0';
Edit3.Text := '0';
exit;
end;
dx := X / J;
Exk := 0;
Fxk := 0;
Fxka := 0;
ms := 0.5; // 計算中間点
if ABS(X) = 1 then ms := 0.697313;
for I := 0 to J - 1 do begin // 積分の範囲のは ms * dx から X - dx * ms 迄です。
t := (I + ms) * dx; // 計算点を中間点とする事で計算精度高くすると同時に
t2 := t * t; // X=1 の時のゼロでの除算の防止をします。
S1 := (1 - t2);
S2 := (1 - m * t2);
if s2 < 0 then break;
S3 := (1 - A1 * t2);
LA := sqrt(S2 / S1);
Exk := Exk + LA * dx; // 第二種楕円積分
LB := sqrt(S1 * S2);
if (m < 1) or (abs(X) < 1) then begin
Fxk := Fxk + dx / LB; // 第一種楕円積分
if S3 > 0 then Fxka := Fxka + dx / LB / S3; // 第三種楕円積分
end;
end;
t2 := arcsin(t - dx) / pi * 180;
labelededit5.Text := floatTostr(t2);
if (m = 1) and (abs(X) = 1) then begin // ヤコービの標準形の場合 X = 1 だけで 分母がゼロが
Edit1.Text := '∞'; // 発生し∞になるのですが、K=1 で X=1の時のみ∞とします。
Edit3.Text := '∞'; // ルジャンドルの標準形に合わせました。
end
else begin
Edit1.Text := floattostr(Fxk);
Edit3.Text := floattostr(Fxka);
end;
Edit2.Text := floattostr(Exk);
if A1 * X * X = 1 then Edit3.Text := '∞';
if A1 * X * X > 1 then Edit3.Text := 'αの値が大きすぎます。';
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
Elliptic;
end;
end.
90°分割プログラム 多倍長演算
// 2021/ 1 / 6 半径入力の追加 // 2020/12/20 ルーチンの整理 // 2020/12/10 無限大の出力に符号追加 //-------------------------------------------------------------------------------------- // 第一種第二種第三種楕円積分のプログラム // 多倍長演算にMPArithを使用しています。 // uses に mp_types, mp_real の追加が必要です。 // MPArith については下記を参照してください。 // "https://web.archive.org/web/20181215233944/http://wolfgang-ehrhardt.de/mp_intro.html" //--------------------------------------------------------------------------------------- unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, mp_types, mp_real, mp_base; type TForm1 = class(TForm) Edit1: TEdit; Edit2: TEdit; Edit3: TEdit; Edit4: TEdit; Edit5: TEdit; Edit6: TEdit; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; k_Edit3 : TLabeledEdit; LabeledEdit4: TLabeledEdit; LabeledEdit5: TLabeledEdit; Button1: TButton; Button2: TButton; Button3: TButton; Button4: TButton; Label1: TLabel; Label2: TLabel; Label3: TLabel; Label4: TLabel; Label5: TLabel; Label6: TLabel; Label7: TLabel; RadioButton1: TRadioButton; RadioButton2: TRadioButton; Label8: TLabel; aEdit: TLabeledEdit; bEdit: TLabeledEdit; RadioButton3: TRadioButton; procedure Button1Click(Sender: TObject); procedure Button2Click(Sender: TObject); procedure Button3Click(Sender: TObject); procedure Button4Click(Sender: TObject); procedure FormCreate(Sender: TObject); procedure FormCloseQuery(Sender: TObject; var CanClose: Boolean); private { Private 宣言 } function datacheck: boolean; procedure Ddatainput; procedure calc_Third_elliptic_integral(a, qb, m: double); procedure Mdatainput; procedure Mcalc_Third_elliptic_integral(ma, mqb, mm: mp_float); public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses Math; var btn2F : boolean = False; // 積分範囲Ｘの計算フラグ Xstr : string; // Ｘのtextバックアップ // 積分範囲Ｘのφ(deg)変換値 MpXtoDeg : mp_float; DbXtoDeg : double; // Carlson's Elliptic Integral RJ procedure MRJ(x11, y11, z11, p11: mp_float; var rj: mp_float); var s, fa, rk : mp_float; la, mu, ss : mp_float; al, be : mp_float; r1, a1, b1 : mp_float; a2, b2, mv, s1 : mp_float; rc, r0 : mp_float; s12, s13, s14 : mp_float; s15, s16 : mp_float; x2, y2, z2 : mp_float; x3, y3, z3 : mp_float; s2, s3, p2, p3 : mp_float; s4, s5 : mp_float; x31, y31, z31, p31 : mp_float; s22, s23, s2s3 : mp_float; t0, t1, t2, t3 : mp_float; one : mp_float; x1, y1, z1, p1 : mp_float; procedure rcab; begin // rc := 1; mpf_set1(rc); // a1 := al; mpf_copy(al, a1); // b1 := be; mpf_copy(be, b1); repeat // r1 := rc; mpf_copy(rc, r1); // la := 2 * sqrt(a1 * b1) + b1; mpf_mul(a1, b1, t0); mpf_sqrt(t0, t1); mpf_mul_int(t1, 2, t2); mpf_add(t2, b1, la); // a2 := (a1 + la) / 4; mpf_add(a1, la, t3); mpf_div_int(t3, 4, a2); // b2 := (b1 + la) / 4; mpf_add(b1, la, t0); mpf_div_int(t0, 4, b2); // mv := (a1 + 2 * b1) / 3; mpf_mul_int(b1, 2, t1); mpf_add(t1, a1, t2); mpf_div_int(t2, 3, mv); // s1 := (b1 - a1) / (3 * mv); mpf_sub(b1, a1, t3); mpf_mul_int(mv, 3, t0); mpf_div(t3, t0, s1); // s12 := s1 * s1; mpf_sqr(s1, s12); // s13 := s12 * s1; mpf_mul(s12, s1, s13); // s14 := s13 * s1; mpf_mul(s13, s1, s14); // s15 := s14 * s1; mpf_mul(s14, s1, s15); // s16 := s15 * s1; mpf_mul(s15, s1, s16); // rc := (1 + 3 * s12 / 10 + s13 / 7 + 3 * s14 / 8 + 9 * s15 / 22 + 159 * s16 / 208) / sqrt(mv); mpf_mul_int(s12, 3, t0); mpf_div_int(t0, 10, t1); // 3 * s12 / 10 mpf_div_int(s13, 7, t2); // s13 / 7 mpf_mul_int(s14, 3, t0); mpf_div_int(t0, 8, t3); // 3 * s14 / 8 mpf_add(one, t1, t0); // 1 + 3 * s12 / 10 mpf_add(t0, t2, t1); // 1 + 3 * s12 / 10 + s13 / 7 mpf_add(t1, t3, t0); // 1 + 3 * s12 / 10 + s13 / 7 + 3 * s14 / 8 mpf_mul_int(s15, 9, t1); mpf_div_int(t1, 22, t2); // 9 * s15 / 22 mpf_mul_int(s16, 159, t1); mpf_div_int(t1, 208, t3); // 159 * s16 / 208 mpf_add(t0, t2, t1); // 1 + 3 * s12 / 10 + s13 / 7 + 3 * s14 / 8 + 9 * s15 / 22 mpf_add(t1, t3, t0); // 1 + 3 * s12 / 10 + s13 / 7 + 3 * s14 / 8 + 9 * s15 / 22 + 159 * s16 / 208 mpf_sqrt(mv, t1); // sqrt(mv) mpf_div(t0, t1, rc); // Σ/ sqrt(mv) // a1 := a2; mpf_copy(a2, a1); // b1 := b2; mpf_copy(b2, b1); // until r1 = rc; until mpf_is_eq(r1, rc); end; procedure sadd; begin // x31 := x31 * x3; mpf_mul(x31, x3, x31); // y31 := y31 * y3; mpf_mul(y31, y3, y31); // z31 := z31 * z3; mpf_mul(z31, z3, z31); // p31 := p31 * p3; mpf_mul(p31, p3, p31); // ss := (x31 + y31 + z31 + p31); mpf_add(x31, y31, t0); mpf_add(z31, p31, t1); mpf_add(t0, t1, ss); end; begin mpf_init3(s, fa, rk); mpf_init3(la, mu, ss); mpf_init2(al, be); mpf_init3(r1, a1, b1); mpf_init4(a2, b2, mv, s1); mpf_init2(rc, r0); mpf_init3(s12, s13, s14); mpf_init2(s15, s16); mpf_init3(x2, y2, z2); mpf_init3(x3, y3, z3); mpf_init4(s2, s3, p2, p3); mpf_init2(s4, s5); mpf_init4(x31, y31, z31, p31); mpf_init3(s22, s23, s2s3); mpf_init4(t0, t1, t2, t3); mpf_init(one); mpf_init4(x1, y1, z1, p1); mpf_copy(x11, x1); mpf_copy(y11, y1); mpf_copy(z11, z1); mpf_copy(p11, p1); mpf_set1(one); // s := 0; mpf_set0(s); // fa := 3; mpf_set_int(fa, 3); // rj := 0; mpf_set0(rj); repeat // r0 := rj; mpf_copy(rj, r0); // la := sqrt(x1 * y1) + sqrt(x1 * z1) + sqrt(y1 * z1); mpf_mul(x1, y1, t0); mpf_sqrt(t0, t1); mpf_mul(x1, z1, t0); mpf_sqrt(t0, t2); mpf_mul(y1, z1, t0); mpf_sqrt(t0, t3); mpf_add(t1, t2, t0); mpf_add(t0, t3, la); // mu := (x1 + y1 + z1 + 2 * p1) / 5; mpf_mul_int(p1, 2, t0); mpf_add(t0, x1, t1); mpf_add(t1, y1, t0); mpf_add(t0, z1, t1); mpf_div_int(t1, 5, mu); // x2 := (x1 + la) / 4; mpf_add(x1, la, t0); mpf_div_int(t0, 4, x2); // y2 := (y1 + la) / 4; mpf_add(y1, la, t0); mpf_div_int(t0, 4, y2); // z2 := (z1 + la) / 4; mpf_add(z1, la, t0); mpf_div_int(t0, 4, z2); // p2 := (p1 + la) / 4; mpf_add(p1, la, t0); mpf_div_int(t0, 4, p2); // x3 := 1 - x1 / mu; mpf_div(x1, mu, t1); mpf_sub(one, t1, x3); // y3 := 1 - y1 / mu; mpf_div(y1, mu, t1); mpf_sub(one, t1, y3); // z3 := 1 - z1 / mu; mpf_div(z1, mu, t1); mpf_sub(one, t1, z3); // p3 := 1 - p1 / mu; mpf_div(p1, mu, t1); mpf_sub(one, t1, p3); // x31 := x3; mpf_copy(x3, x31); // y31 := y3; mpf_copy(y3, y31); // z31 := z3; mpf_copy(z3, z31); // p31 := 2 * p3; mpf_mul_int(p3, 2, p31); sadd; // s2 := ss / 4; mpf_div_int(ss, 4, s2); sadd; // s3 := ss / 6; mpf_div_int(ss, 6, s3); sadd; // s4 := ss / 8; mpf_div_int(ss, 8, s4); sadd; // s5 := ss / 10; mpf_div_int(ss, 10, s5); // al := (sqrt(x1) + sqrt(y1) + sqrt(z1)) * p1 + sqrt(x1 * y1 * z1); mpf_sqrt(x1, t0); mpf_sqrt(y1, t1); mpf_sqrt(z1, t2); mpf_add(t0, t1, t3); mpf_add(t3, t2, t0); mpf_mul(t0, p1, t1); // (sqrt(x1) + sqrt(y1) + sqrt(z1)) * p1 mpf_mul(x1, y1, t0); mpf_mul(t0, z1, t2); mpf_sqrt(t2, t0); // sqrt(x1 * y1 * z1) mpf_add(t1, t0, t2); // (sqrt(x1) + sqrt(y1) + sqrt(z1)) * p1 + sqrt(x1 * y1 * z1) // al := al * al; mpf_sqr(t2, al); // be := p1 * (p1 + la) * (p1 + la); mpf_add(p1, la, t0); mpf_sqr(t0, t1); mpf_mul(t1, p1, be); rcab; // s22 := 3 * s2 * s2 / 22; mpf_sqr(s2, t0); mpf_mul_int(t0, 3, t1); mpf_div_int(t1, 22, s22); // s23 := s2 * s2 * s2 / 10; mpf_expt_int(s2, 3, t0); mpf_div_int(t0, 10, s23); // s2s3 := s2 * s3 * 3 / 13; mpf_mul(s2, s3, t0); mpf_mul_int(t0, 3, t1); mpf_div_int(t1, 13, s2s3); // s := s + fa * rc; mpf_mul(fa, rc, t1); mpf_add(s, t1, s); // rk := 1 + 3 * s2 / 7 + s3 / 3 + s22 + s2s3 + 3 * s4 / 11 + 3 * s5 / 13 - s23; mpf_mul_int(s2, 3, t0); mpf_div_int(t0, 7, t1); // 3 * s2 / 7 mpf_div_int(s3, 3, t2); // s3 / 3 mpf_add(one, t1, t0); // 1 + 3 * s2 / 7 t0 mpf_add(t0, t2, t3); // 1 + 3 * s2 / 7 + s3 / 3 t3 mpf_add(t3, s22, t1); // 1 + 3 * s2 / 7 + s3 / 3 + s22 t1 mpf_add(t1, s2s3, t3); // 1 + 3 * s2 / 7 + s3 / 3 + s22 + s2s3 t3 mpf_mul_int(s4, 3, t0); mpf_div_int(t0, 11, t1); // 3 * s4 / 11 mpf_mul_int(s5, 3, t0); mpf_div_int(t0, 13, t2); // 3 * s5 / 13 mpf_add(t3, t1, t0); // 1 + 3 * s2 / 7 + s3 / 3 + s22 + s2s3 + 3 * s4 / 11 mpf_add(t0, t2, t3); // 1 + 3 * s2 / 7 + s3 / 3 + s22 + s2s3 + 3 * s4 / 11 + 3 * s5 / 13 mpf_sub(t3, s23, rk); // 1 + 3 * s2 / 7 + s3 / 3 + s22 + s2s3 + 3 * s4 / 11 + 3 * s5 / 13 - s23 // fa := fa / 4; mpf_div_int(fa, 4, fa); // mu := sqrt(1 / (mu * mu * mu)); mpf_expt_int(mu, 3, t0); mpf_div(one, t0, t1); mpf_sqrt(t1, mu); // rj := s + fa / 4 * (rk + 3 * s3 * s3 / 10 + 3 * s2 * s4 / 5) * mu; mpf_div_int(fa, 4, t1); // fa / 4 mpf_sqr(s3, t0); mpf_mul_int(t0, 3, t3); mpf_div_int(t3, 10, t2); // 3 * s3 * s3 / 10 mpf_mul(s2, s4, t0); mpf_mul_int(t0, 3, t3); mpf_div_int(t3, 5, t0); // 3 * s2 * s4 / 5 mpf_add(rk, t2, t3); // rk + 3 * s3 * s3 / 10 mpf_add(t3, t0, t2); // rk + 3 * s3 * s3 / 10 + 3 * s2 * s4 / 5 mpf_mul(t1, t2, t3); // fs / 4 * (rk + 3 * s3 * s3 / 10 + 3 * s2 * s4 / 5) mpf_mul(t3, mu, t0); // fs / 4 * (rk + 3 * s3 * s3 / 10 + 3 * s2 * s4 / 5) * mu mpf_add(s, t0, rj); // s + fs / 4 * (rk + 3 * s3 * s3 / 10 + 3 * s2 * s4 / 5) * mu // x1 := x2; mpf_copy(x2, x1); // y1 := y2; mpf_copy(y2, y1); // z1 := z2; mpf_copy(z2, z1); // p1 := p2; mpf_copy(p2, p1); // until rj = r0; until mpf_is_eq(rj, r0); // Edit2.Text := string(mpf_decimal(fa, 50)); mpf_clear3(s, fa, rk); mpf_clear3(la, mu, ss); mpf_clear2(al, be); mpf_clear3(r1, a1, b1); mpf_clear4(a2, b2, mv, s1); mpf_clear2(rc, r0); mpf_clear3(s12, s13, s14); mpf_clear2(s15, s16); mpf_clear3(x2, y2, z2); mpf_clear3(x3, y3, z3); mpf_clear4(s2, s3, p2, p3); mpf_clear2(s4, s5); mpf_clear4(x31, y31, z31, p31); mpf_clear3(s22, s23, s2s3); mpf_clear4(t0, t1, t2, t3); mpf_clear(one); mpf_clear4(x1, y1, z1, p1); end; // Carlson's Elliptic Integral RF procedure MRF(x11, y11, z11: mp_float; var rf: mp_float); var la, mu : mp_float; x2, y2, z2 : mp_float; x3, y3, z3 : mp_float; s2, s3 : mp_float; r0 : mp_float; s22, s23, s2s3, s32 : mp_float; one : mp_float; t0, t1, t2 : mp_float; x1, y1, z1 : mp_float; begin mpf_init2(la, mu); mpf_init3(x2, y2, z2); mpf_init3(x3, y3, z3); mpf_init2(s2, s3); mpf_init(r0); mpf_init4(s22, s23, s2s3, s32); mpf_init(one); mpf_init3(t0, t1, t2); mpf_init3(x1, y1, z1); // rf := 0; mpf_set0(rf); mpf_copy(x11, x1); mpf_copy(y11, y1); mpf_copy(z11, z1); repeat // r0 := rf; mpf_copy(rf, r0); // la := sqrt(x1 * y1) + sqrt(x1 * z1) + sqrt(y1 * z1); mpf_mul(x1, y1, s22); mpf_mul(x1, z1, s23); mpf_mul(y1, z1, s32); mpf_sqrt(s22, t0); mpf_sqrt(s23, t1); mpf_add(t0, t1, t2); mpf_sqrt(s32, t0); mpf_add(t2, t0, la); // mu := (x1 + y1 + z1) / 3; mpf_add(x1, y1, t2); mpf_add(t2, z1, t1); mpf_div_int(t1, 3, mu); // x2 := (x1 + la) / 4; mpf_add(x1, la, t0); mpf_div_int(t0, 4, x2); // y2 := (y1 + la) / 4; mpf_add(y1, la, t0); mpf_div_int(t0, 4, y2); // z2 := (z1 + la) / 4; mpf_add(z1, la, t0); mpf_div_int(t0, 4, z2); mpf_set1(one); // x3 := 1 - x2 / mu; mpf_div(x2, mu, t2); mpf_sub(one, t2, x3); // y3 := 1 - y2 / mu; mpf_div(y2, mu, t2); mpf_sub(one, t2, y3); // z3 := 1 - z2 / mu; mpf_div(z2, mu, t2); mpf_sub(one, t2, z3); // s2 := (x3 * x3 + y3 * y3 + z3 * z3) / 4; mpf_sqr(x3, t0); mpf_sqr(y3, t1); mpf_add(t0, t1, t2); mpf_sqr(z3, t0); mpf_add(t2, t0, t1); mpf_div_int(t1, 4, s2); // s3 := (x3 * x3 * x3 + y3 * y3 * y3 + z3 * z3 * z3) / 6; mpf_expt_int(x3, 3, t0); mpf_expt_int(y3, 3, t1); mpf_add(t0, t1, t2); mpf_expt_int(z3, 3, t0); mpf_add(t0, t2, t1); mpf_div_int(t1, 6, s3); // s22 := s2 * s2 / 6; mpf_sqr(s2, t0); mpf_div_int(t0, 6, s22); // s23 := 5 * s2 * s2 * s2 / 26; mpf_expt_int(s2, 3, t0); mpf_mul_int(t0, 5, t1); mpf_div_int(t1, 26, s23); // s32 := 3 * s3 * s3 / 26; mpf_sqr(s3, t0); mpf_mul_int(t0, 3, t1); mpf_div_int(t1, 26, s32); // s2s3 := s2 * s3 * 3 / 11; mpf_mul(s2, s3, t0); mpf_mul_int(t0, 3, t1); mpf_div_int(t1, 11, s2s3); // rf := (1 + s2 / 5 + s3 / 7 + s22 + s2s3 + s23 + s32) / sqrt(mu); mpf_div_int(s2, 5, t0); mpf_div_int(s3, 7, t1); mpf_add(t0, t1, t2); mpf_add(t2, one, t1); mpf_add(t1, s22, t0); mpf_add(t0, s2s3, t2); mpf_add(t2, s23, t1); mpf_add(t1, s32, t0); mpf_sqrt(mu, t2); mpf_div(t0, t2, rf); // x1 := x2; mpf_copy(x2, x1); // y1 := y2; mpf_copy(y2, y1); // z1 := z2; mpf_copy(z2, z1); // until rf = r0; until mpf_is_eq(rf, r0); mpf_clear2(la, mu); mpf_clear3(x2, y2, z2); mpf_clear3(x3, y3, z3); mpf_clear2(s2, s3); mpf_clear(r0); mpf_clear4(s22, s23, s2s3, s32); mpf_clear(one); mpf_clear3(t0, t1, t2); mpf_clear3(x1, y1, z1); end; // 多倍長 第一、二、三種楕円積分 // ma 特性 三種 // mq 角度rad // mm パラメーター k^2 procedure TForm1.Mcalc_Third_elliptic_integral(ma, mqb, mm: mp_float); label LEXIT, MNo2; var J : integer; mj : mp_int; mq : mp_float; ms, ms2, ms3 : mp_float; mc2 : mp_float; mrf0, mrj0 : mp_float; mafk, maek : mp_float; m1mk2, m1mas2 : mp_float; mak90 : mp_float; mONE, mTMP : mp_float; mfqk, mfek : mp_float; mfqk90 : mp_float; meqk : mp_float; meq : mp_float; mps2 : mp_float; ALFRG : Integer; // 第三種計算フラグ 0 正常 1 ±∞ 2 第三種aの値大 演算不可 ALFQK : Integer; // 第一種計算フラグ 0 正常 1 ±∞ begin mp_init(mj); mpf_init(mq); mpf_init3(ms, ms2, ms3); mpf_init(mc2); mpf_init2(mrf0, mrj0); mpf_init2(mafk, maek); mpf_init2(m1mk2, m1mas2); mpf_init2(mONE, mTMP); mpf_init(mak90); mpf_init(meq); mpf_init(mps2); mpf_init2(mfqk, mfek); mpf_init(mfqk90); mpf_init(meqk); // 第一種第三種楕円積分 多倍長 ------------------------------------- ALFRG := 0; ALFQK := 0; mpf_set_pi(mps2); // πセット mpf_div_int(mps2, 2, mps2); // π / 2 mpf_abs(mqb, mq); // q = abs(θ) mpf_div(mq, mps2, mTMP); // mTMP = q / (π / 2) { もし積分角90°でJ = 1にならない場合、'q = q + q * 2^(1-q.bitprec)) として計算します。 ( mpf_get_default_prec Return current default (bit) precision, initial=240 ) mpf_div(mq, mps2, mTMP); を下記の7行と置き換えます。 } { J := mpf_get_default_prec; // J = 240 default J := 1 - J; // 1 - J mpf_set_int(mTMP,J); // (1 - J) -> mp_float mpf_exp2(mTMP, mTMP); // EPSILON = 2^(1 - J) mpf_mul(mq, mTMP, mTMP); // q" = q * EPSILON mpf_add(mq, mTMP, mTMP); // 'q = q + q" mpf_div(mTMP, mps2, mTMP); // mTMP = 'q / (π/2) } mpf_trunc(mTMP, mj); // 小数点以下切り捨て J := mp_get_int(mj); // 多倍長整数 -> integer if J > 0 then begin // 90°より大きかったら mpf_set1(ms2); // sin^2φ = 1 end else begin mpf_sin(mq, ms); // sinφ mpf_sqr(ms, ms2); // sin^2φ end; mpf_mul(mm, ms2, mTMP); // k^2sin^2φ mpf_set1(mONE); // 1 mpf_sub(mONE, mTMP, m1mk2); // 1 - k^2sin^2φ mpf_mul(ma, ms2, mTMP); // a*sin^2φ mpf_sub(mONE, mTMP, m1mas2); // 1 - a*sin^2φ if s_mpf_is_le0(m1mas2) then begin // (1 - a*sin^2φ) <= 0 なら 第三種処理 if s_mpf_is0(m1mas2) then ALFRG := 1 // 第三種∞か-∞フラグ else ALFRG := 2; // 第三種 a特性(n) 大きすぎ end; mpf_set0(mak90); mpf_set0(mfqk90); if J > 0 then begin // 積分角が90°以上なら 90°(π/2) 積分 if s_mpf_is_le0(m1mk2) then begin ALFQK := 1; ALFRG := 1; end else begin mpf_set0(mc2); // cos^2(90°) = 0 mpf_set1(ms); // sin(90°) = 1 mpf_set1(ms3); // sin^3(90°) = 1 MRF(mc2, m1mk2, mONE, mrf0); // RF(x,y,z) mpf_mul(ms, mrf0, mTMP); // sinφ*RF(x,y,z) mpf_copy(mrf0, mfqk90); // F(90°,k) = RF(x,y,z) * sin(90°) = RF(x,y,z) end; if ALFRG = 0 then begin MRJ(mc2, m1mk2, mONE, m1mas2, mrj0); // RJ(x,y,z,ρ) mpf_div_int(ma, 3, ms2); // a/3 mpf_mul(ms2, ms3, mc2); // a/3 * sin^3φ mpf_mul(mc2, mrj0, ms3); // a/3 * sin^3φ * RJ(x,y,z,ρ) mpf_add(mtmp, ms3, mak90); // F(90°,k) + a/3 * sin^3φ * RJ(x,y,z,ρ) end; end; if J mod 2 <> 0 then begin // eq = (j + 1) * pi / 2 - q 奇数象限積分角計算 mpf_mul_int(mps2, J + 1, mTMP); mpf_sub(mTMP, mq, meq); end else begin // eq = q - (pi / 2 * j) 偶数象限積分角計算 mpf_mul_int(mps2, J, mTMP); mpf_sub(mq, mTMP, meq); end; mpf_cos(meq, ms); // cosφ mpf_sqr(ms, mc2); // cos^2φ mpf_sin(meq, ms); // sinφ mpf_sqr(ms, ms2); // sin^2φ mpf_mul(ms2, ms, ms3); // sin^3φ mpf_mul(mm, ms2, mTMP); // k^2sin^2φ mpf_set1(mONE); // 1 mpf_sub(mONE, mTMP, m1mk2); // 1 - k^2sin^2φ if s_mpf_is_neg(m1mk2) then mpf_set0(m1mk2); mpf_mul(ma, ms2, mTMP); // a*sin^2φ mpf_sub(mONE, mTMP, m1mas2); // 1 - a*sin^2φ if ALFQK = 0 begin MRF(mc2, m1mk2, mONE, mrf0); // RF(x,y,z) mpf_mul(ms, mrf0, mTMP); // fek := s * rf0; mpf_copy(mTMP, mfek); // F(eq, k) end; if ALFRG = 0 then begin MRJ(mc2, m1mk2, mONE, m1mas2, mrj0); // RJ(x,y,z,ρ) mpf_div_int(ma, 3, ms2); // a/3 mpf_mul(ms2, ms3, mc2); // a/3 * sin^3φ mpf_mul(mc2, mrj0, ms3); // a/3 * sin^3φ * RJ(x,y,z,ρ) mpf_add(mTMP, ms3, maek); // F(eq, k) + a/3 * sin^3φ * RJ(x,y,z,ρ) end; if J mod 2 <> 0 then begin // 第２,第４象限の積分値 if ALFRG = 0 then begin mpf_mul_int(mak90, j + 1, mTMP); mpf_sub(mTMP, maek, mafk); // Π(a,φ,k) = mafk := (j + 1) * mafk90 - maek; end; if ALFQK = 0 then begin mpf_mul_int(mfqk90, j + 1, mTMP); mpf_sub(mTMP, mfek, mfqk); // F(φ,k) = mfqk := (j + 1) * mfqk90 - mfek; end; end else begin // 第1,第3象限の積分値 if ALFRG = 0 then begin mpf_mul_int(mak90, j, mTMP); mpf_add(mTMP, maek, mafk); // Π(a,φ,k) = afk := j * mafk90 + maek; end; if ALFQK = 0 then begin mpf_mul_int(mfqk90, j, mTMP); mpf_add(mTMP, mfek, mfqk); // F(φ,k) = mfqk := j * mfqk90 + mfek; end; end; if s_mpf_is_neg(mqb) then begin // 積分方向で符号設定 s_mpf_chs(mafk); s_mpf_chs(mfqk); end; LEXIT: case ALFRG of // 第三種 0 : Edit2.Text := string(mpf_decimal_alt(mafk, 51)); 1 : if s_mpf_is_ge0(mqb) then Edit2.Text := 'INF' else Edit2.Text := '-INF'; 2 : Edit2.Text := 'a(特性)の値が大きすぎます。' end; case ALFQK of // 第一種 0 : Edit6.Text := string(mpf_decimal_alt(mfqk, 51)); 1 : if s_mpf_is_ge0(mqb) then Edit6.Text := 'INF' else Edit6.Text := '-INF'; end; //------------------------------------------------------------------ // 第二種楕円積分 多倍長 ------------------------------------------- ALFRG := 0; // 第二種計算フラグ 0 正常 1 kの値大 演算不可 // J := mp_get_int(mj); mpf_set0(mfqk90); mpf_set0(mfqk); if J > 0 then begin // 90°以上なら mpf_set_int(mfqk, J); // mfqk = J mpf_mul_int(mps2, J, ms3); // J * π / 2 if mpf_is_eq_rel(mq, ms3) and mpf_is1(mm) then begin // mpf_is_eq_rel 微小誤差は＝判定 // Doubleの演算ではビット数が少ないので＝となりますが、ビット数が非常に多いので、最終ビットに差がでます goto MNo2; // 答えはj 終了処理 end else if mpf_is_gt(mm, mONE) then begin // m > 1 なら ALFRG := 1; // エラーフラグセット goto MNo2; // 終了処理 end else begin // m <= 1 なら 90°(π/2) 積分 if mpf_is1(mm) then // m = 1 なら mpf_set1(mfqk90) // fqk90 = 1 else begin // m < 1 なら 90°積分値計算 mpf_set0(mc2); // cos^2(90°) = 0 mpf_set1(ms); // sin(90°) = 1 mpf_set1(ms3); // sin^3(90°) = 1 mpf_sub(mONE, mm, m1mk2); // 1 - k^2 MRF(mc2, m1mk2, mONE, mrf0); // RF(x,y,z) MRJ(mc2, m1mk2, mONE, mONE, mrj0); // RD(x,y,z) = RJ(x,y,z,z) mpf_mul(ms, mrf0, mTMP); // sinφ*RF(x,y,z) mpf_div_int(mm, 3, ms2); // k^2 /3 mpf_mul(ms2, ms3, mc2); // k^2 /3 *sin^3φ mpf_mul(mc2, mrj0, ms3); // k^2 /3 *sin^3φ * RD(x,y,z) mpf_sub(mTMP, ms3, mfqk90); // E(90°,K) = sinφ*RF(x,y,z) - k^2 /3 *sin^3φ * RD(x,y,z) end; end; end; if j mod 2 <> 0 then begin // 'φ = eq = (j + 1) * pi / 2 - q 第２,第４象限の積分角度 mpf_mul_int(mps2, J + 1, mTMP); mpf_sub(mTMP, mq, meq); end else begin // 'φ = eq = q - (pi / 2 * j) 第1,第3象限の積分角度 mpf_mul_int(mps2, J, mTMP); mpf_sub(mq, mTMP, meq); end; mpf_cos(meq, ms); // cosφ mpf_sqr(ms, mc2); // cos^2φ mpf_sin(meq, ms); // sinφ mpf_sqr(ms, ms2); // sin^2φ mpf_mul(ms2, ms, ms3); // sin^3φ mpf_mul(mm, ms2, mTMP); // k^2sin^2φ // mpf_set1(mONE); // 1 mpf_sub(mONE, mTMP, m1mk2); // 1 - k^2sin^2φ if s_mpf_is_neg(m1mk2) then mpf_set0(m1mk2); if s_mpf_is_ge0(m1mk2) then begin // 1 - k^2sin^2φ >= 0 なら 象限の積分 if mpf_is_eq(mm, mONE) then begin // m = 1 なら mpf_sin(meq, maek); // aek = sin(φ) end else begin // m <> 1 なら MRF(mc2, m1mk2, mONE, mrf0); MRJ(mc2, m1mk2, mONE, mONE, mrj0); // RD(x,y,z) = RJ(x,y,z,z) mpf_mul(ms, mrf0, mTMP); // F(φ,K) := s * rf0; mpf_div_int(mm, 3, ms2); // k^2 /3 mpf_mul(ms2, ms3, mc2); // k^2 /3 *sin^2φ mpf_mul(mc2, mrj0, ms3); // k^2 /3 *sin^3φ * RD(x,y,z) mpf_sub(mTMP, ms3, maek); // sinφ*RF(x,y,z) - k^2 /3 *sin^3φ * RD(x,y,z) end; end else begin ALFRG := 1; goto MNo2; end; if j mod 2 <> 0 then begin // E(φ,K) = (j + 1) * E(90°,K) - E('φ,K) 奇数象限 mpf_mul_int(mfqk90, j + 1, mTMP); mpf_sub(mTMP, maek, mfqk); end else begin // E(φ,K) = j * E(90°,K) + E('φ,K); 偶数象限 mpf_mul_int(mfqk90, j, mTMP); mpf_add(mTMP, maek, mfqk); end; MNo2: if s_mpf_is_neg(mqb) then s_mpf_chs(mfqk); // 積分方向符号設定 case ALFRG of // 第二種 0: Edit4.Text := string(mpf_decimal_alt(mfqk, 51)); 1: Edit4.Text := 'k(離心率)の値が大きすぎます。' end; //----------------------------------------------------------------- mp_clear(mj); mpf_clear(mq); mpf_clear3(ms, ms2, ms3); mpf_clear(mc2); mpf_clear2(mrf0, mrj0); mpf_clear2(mafk, maek); mpf_clear2(m1mk2, m1mas2); mpf_clear(mak90); mpf_clear2(mONE, mTMP); mpf_clear(meq); mpf_clear(mps2); mpf_clear2(mfqk, mfek); mpf_clear(mfqk90); mpf_clear(meqk); end; // 多倍長入力処理と多倍長楕円積分 // ma 特性 三種 // mq 角度rad // mm パラメーター k^2 procedure TForm1.Mdatainput; var ch : integer; msn, mpi, mk : mp_float; meq, m90, mqg : mp_float; deg : mp_float; ma, mqb, mm : mp_float; ma0, mb0, mone : mp_float; mone : mp_float; mj : mp_int; c : char; l : integer; kss, kstr : string; mqbmax, tmp : mp_float; begin mpf_init3(msn, mpi, mk); mpf_init4(meq, m90, mqg, deg); mpf_init3(ma, mqb, mm); mpf_init3(ma0, mb0, mone); mp_init(mj); mpf_init2(mqbmax, tmp); mpf_set1(mone); mpf_set_pi(mpi); // pi // 特性α mpf_read_decimal(ma, PAnsiChar(ansistring(LabeledEdit1.Text + #00))); // 積分範囲 mq if btn2F then // Ｘの範囲計算なら mpf_copy(MpXtoDeg, deg) else begin // degの範囲なら mpf_read_decimal(deg, PAnsiChar(ansistring(LabeledEdit2.Text + #00))); mpf_copy(deg, MpXtoDeg) end; mpf_div_int(deg, 180, msn); // deg -> rad msn = phi / 180 mpf_mul(msn, mpi, mqb); // mq = msn * pi 積分角度(rad) // パラメーターm if radiobutton1.Checked then begin // 離心率k指定 // c := #0; kstr := k_edit.Text; l := length(kstr); // 文字の長さ取得 c := kstr[l]; // iの文字確認 if (c = 'i') or (c = 'I') then begin // i虚数指定だったら 末尾の文字取得 c := 'i'; // 虚数フラグセット kss := copy(kstr, 1, l - 1); // iの前までコピー end else Kss := kstr; mpf_read_decimal(mk, PAnsiChar(ansistring(kss + #00))); mpf_sqr(mk, mm); // m = k^2 if c = 'i' then mpf_chs(mm, mm); // m := -m if mpf_is_gt(mm, mone) then begin // if m > 1 then begin mpf_abs(mk, tmp); // abs(k) mpf_div(mone, tmp, tmp); // 1 / k mpf_arcsin(tmp, mqbmax); // arcsin(1/k) mpf_abs(qb, tmp); // abs(qb) if mpf_is_gt(tmp, mqbmax) then begin // if abs(deg) > qbmax then begin if s_mpf_is_neg(deg) then mpf_chs(mqbmax, mqbmax); // if deg < 0 then qb := -qb; mpf_copy(mqbmax, mqb); // qb := qbmax; end; end; end; if radiobutton2.Checked then begin // パラメーターm指定 mpf_read_decimal(mm, PAnsiChar(ansistring(LabeledEdit5.Text + #00))); if s_mpf_is_gt0(mm) then mpf_sqrt(mm, mk); // if m > 0 then k := sqrt(m); if mpf_is_gt(mm, mone) then begin // if m > 1 then begin mpf_div(mone, mk, tmp); // 1/k mpf_arcsin(tmp, mqbmax); // 積分可能最大値 arcsin(1/k) mpf_abs(mqb, tmp); // abs(qb) if mpf_is_gt(tmp, mqbmax) then begin // if abs(qb) > qbmax then begin if s_mpf_is_neg(deg) then mpf_chs(mqbmax, mqbmax); // if deg < 0 then qb := -qb; mpf_copy(mdegmax, deg); // qb := qbmax; end; end; end; if radiobutton3.Checked then begin // 半径(a,b)指定 mpf_read_decimal(ma0, PAnsiChar(ansistring(aEdit.Text + #00))); mpf_read_decimal(mb0, PAnsiChar(ansistring(bEdit.Text + #00))); mpf_mul(mb0, mb0, mb0); mpf_mul(ma0, ma0, ma0); mpf_div(mb0, ma0, mm); mpf_sub(mone, mm, mm); end; mpf_div(mqb, mpi, tmp); // qb -> qb / pi mpf_mul_int(tmp, 180, deg); // deg = qb / pi * 180 積分角度(deg) //----- start --- deg -> X 計算 表示用 ------------- mpf_abs(deg, mqg); // qb = abs(deg) mpf_div_int(mqg, 90, meq); // eq = qb / 90 mpf_trunc(meq, mj); // j = int(eq) ch := mp_get_int(mj); // j -> ch integer mpf_set_int(m90, 90); if ch mod 2 <> 0 then begin // eq = (j + 1) * 90 - qb 奇数象限 mpf_mul_int(m90, ch + 1, m90); mpf_sub(m90, mqg, meq); end else begin // eq = qb - (90 * j) 偶数象限 mpf_mul_int(m90, ch, m90); mpf_sub(mqg, m90, meq); end; mpf_div_int(meq, 180, msn); // sn = eq / 180 mpf_mul(msn, mpi, meq); // eq = sn * pi mpf_sin(meq, msn); // sn = sin(eq) if ch mod 2 <> 0 then begin // eq = (ch + 1) - sin(eq); 奇数象限 mpf_set_int(m90, ch + 1); mpf_sub(m90, msn, msn); end else begin // ch + sin(eq) 偶数象限 mpf_add_int(msn, ch, msn); end; if s_mpf_is_neg(deg) then mpf_chs(msn, msn); // 符号設定 //----- end --- deg -> X -------------------------- if not btn2F then begin Xstr := string(mpf_decimal_alt(msn, 70)); // Xの値文字バックアップ Label2.Caption := '積分範囲 φ= ' + string(mpf_decimal_alt(deg, 20)) + ' deg'; Label3.Caption := '積分範囲 Ｘ= ' + string(mpf_decimal_alt(msn, 20)); end; // ---- max α calc ---------------------------- mpf_div_int(deg, 180, msn); // deg -> rad msn = phi / 180 mpf_mul(msn, mpi, mqb); // mq = msn * pi 積分角度(rad) mpf_set_pi(m90); // pi mpf_div_int(m90, 2, m90); // pi/2 if mpf_is_ge(mqb, m90) then mpf_set1(msn) // 1 else mpf_sin(mqb, msn); // sinφ mpf_sqr(msn, meq); // sin^2(φ) if s_mpf_is_gt0(meq) then begin // sin^2(φ) > 0 mpf_inv(meq, mqg); // 1 / sin^2(φ) Label6.Caption := 'α(特性n)の上限値= ' + string(mpf_decimal_alt(mqg, 20)); end else Label6.Caption := 'α(特性n)の上限値= ∞'; // 多倍長楕円積分 Mcalc_Third_elliptic_integral(ma, mqb, mm); //----------------------------------------------- button3.Enabled := true; mpf_clear3(msn, mpi, mk); mpf_clear4(meq, m90, mqg, deg); mpf_clear3(ma, mqb, mm); mpf_clear3(ma0, mb0, mone); mp_clear(mj); mpf_clear2(mqbmax, tmp); end; //============================================================================== // Carlson's Elliptic Integral RJ function RJ(x1, y1, z1, p1: double): double; var s, fa, rj, rk : double; la, mu : double; al, be : double; r1, a1, b1 : double; a2, b2, mv, s1 : double; rc, r0 : double; s12, s13, s14 : double; s15, s16 : double; x2, y2, z2 : double; x3, y3, z3 : double; s2, s3, p2, p3 : double; s4, s5 : double; x31, y31, z31, p31 : double; s22, s23, s2s3 : double; procedure rcab; begin rc := 1; a1 := al; b1 := be; repeat r1 := rc; la := 2 * sqrt(a1 * b1) + b1; a2 := (a1 + la) / 4; b2 := (b1 + la) / 4; mv := (a1 + 2 * b1) / 3; s1 := (b1 - a1) / (3 * mv); s12 := s1 * s1; s13 := s12 * s1; s14 := s13 * s1; s15 := s14 * s1; s16 := s15 * s1; rc := (1 + 3 * s12 / 10 + s13 / 7 + 3 * s14 / 8 + 9 * s15 / 22 + 159 * s16 / 208) / sqrt(mv); a1 := a2; b1 := b2; until r1 = rc; end; function ss: double; begin x31 := x31 * x3; y31 := y31 * y3; z31 := z31 * z3; p31 := p31 * p3; result := (x31 + y31 + z31 + p31); end; begin s := 0; fa := 3; rj := 0; repeat r0 := rj; la := sqrt(x1 * y1) + sqrt(x1 * z1) + sqrt(y1 * z1); mu := (x1 + y1 + z1 + 2 * p1) / 5; x2 := (x1 + la) / 4; y2 := (y1 + la) / 4; z2 := (z1 + la) / 4; p2 := (p1 + la) / 4; x3 := 1 - x1 / mu; y3 := 1 - y1 / mu; z3 := 1 - z1 / mu; p3 := 1 - p1 / mu; x31 := x3; y31 := y3; z31 := z3; p31 := 2 * p3; s2 := ss / 4; s3 := ss / 6; s4 := ss / 8; s5 := ss / 10; al := (sqrt(x1) + sqrt(y1) + sqrt(z1)) * p1 + sqrt(x1 * y1 * z1); al := al * al; be := p1 * (p1 + la) * (p1 + la); rcab; s22 := 3 * s2 * s2 / 22; s23 := s2 * s2 * s2 / 10; s2s3 := s2 * s3 * 3 / 13; s := s + fa * rc; rk := 1 + 3 * s2 / 7 + s3 / 3 + s22 + s2s3 + 3 * s4 / 11 + 3 * s5 / 13 - s23; fa := fa / 4; mu := sqrt(1 / (mu * mu * mu)); rj := s + fa / 4 * (rk + 3 * s3 * s3 / 10 + 3 * s2 * s4 / 5) * mu; x1 := x2; y1 := y2; z1 := z2; p1 := p2; until rj = r0; result := rj; end; // Carlson's Elliptic Integral RF function RF(x1, y1, z1: double): double; var la, mu : double; x2, y2, z2 : double; x3, y3, z3 : double; s2, s3 : double; r0, rf : double; s22, s23, s2s3, s32 : double; begin rf := 0; repeat r0 := rf; la := sqrt(x1 * Y1) + sqrt(x1 * z1) + sqrt(y1 * z1); mu := (x1 + y1 + z1) / 3; x2 := (x1 + la) / 4; y2 := (y1 + la) / 4; z2 := (z1 + la) / 4; x3 := 1 - x2 / mu; y3 := 1 - y2 / mu; z3 := 1 - z2 / mu; s2 := (x3 * x3 + y3 * y3 + z3 * z3) / 4; s3 := (x3 * x3 * x3 + y3 * y3 * y3 + z3 * z3 * z3) / 6; s22 := s2 * s2 / 6; s23 := 5 * s2 * s2 * s2 / 26; s32 := 3 * s3 * s3 / 26; s2s3 := s2 * s3 * 3 / 11; rf := (1 + s2 / 5 + s3 / 7 + s22 + s2s3 + s23 + s32) / sqrt(mu); x1 := x2; y1 := y2; z1 := z2; until rf = r0; result := rf; end; // 第一、二、三種楕円積分 // a 特性 三種 // m パラメーター k^2 // qb rad 角度 procedure TForm1.calc_Third_elliptic_integral(a, qb, m: double); label No2; var // DBL_EPSILON : double; // 最小誤差 J : integer; s, s2, s3 : double; c2 : double; rf0, rj0 : double; afk, aek : double; afk90 : double; q, eq : double; fqk, fek : double; fqk90 : double; rd0 : double; eqk, eek : double; eqk90 : double; pis2 : double; mss2 : double; MKFRG : integer; // 第一種計算フラグ 0 正常 1 ±∞ ALFRG : Integer; // 第三種計算フラグ 0 正常 1 ±∞ 2 第三種aの値大 演算不可 begin // 第一種第三種楕円積分 -------------------------------------------- afk := 0; // 第三種積分値 aek := 0; // 第一種積分値 ALFRG := 0; MKFRG := 0; q := abs(qb); pis2 := pi / 2; // 32bit時 pi/2 > pis2 pi(extended) pis2(double) 64bit時 pi(double) { 32ビットコンパイラの場合 q /(pi/2) の計算は q はdouble pi/2 はextendedで q/(pi/2)の演算はextendedで 演算される為90°180°270°360°の値が1,2,3,4の整数になりませんので pi/2 (extende) -> pis2(double)の 変換をして計算します。 64ビットコンパイラの場合は、全てdoubleになるので問題ありません。 プログラムの修正により積分角90°でJが0になるようならDBL_EPSILONの計算を有効にします } // DBL_EPSILON := power(2, -52); // J := trunc((q + q * DBL_EPSILON ) / (pi / 2)); J := trunc(q / pis2); // 象限計算小数点以下切り捨て 0,1,2,3,4 if J > 0 then begin // 90°以上だったら s2 := 1; // sin^2(90°)=1 end else begin // 90°以下なら s := sin(q); // sin(φ) s2 := s * s; // sin~2(φ) end; if J mod 2 <> 0 then eq := (J + 1) * pis2 - q // 第２,第４象限の積分角度 else eq := q - (pis2 * J); // 第1,第3象限の積分角度 if eq < 0 then eq := 0; // eq に0以下は無いので0以下は誤差なので0設定 if (1 - a * s2) <= 0 then begin // aの値が大きすぎたら if (1 - a * s2) = 0 then begin ALFRG := 1; // 第三種 ∞フラグセット if qb >= 0 then afk := infinity // 第三種 = '∞' else afk := -infinity; // 第三種 = '-∞' end else ALFRG := 2; // 1-a^2*sin^2(φ) がマイナスフラグセット end; afk90 := 0; // 第三種90°積分値 fqk90 := 0; // 第一種90°積分値 if J > 0 then begin // 90°以上だったら 90度の積分計算 if m = 1 then begin if qb > 0 then begin fqk := infinity; afk := infinity; end else begin fqk := -infinity; afk := -infinity; end; MKFRG := 1; ALFRG := 1; // 第三種 ∞フラグセット end else begin rf0 := RF(0, 1 - m, 1); // 90°のRF計算 if ALFRG = 0 then begin // 第三種計算実行なら rj0 := RJ(0, 1 - m, 1, 1 - a * 1); // 90°のRj計算 afk90 := rf0 + a / 3 * rj0; // 90度の積分値 第三種 Π(a, 90°,K) end; fqk90 := rf0; // 90度の積分値 第一種 rf0 * sin90°= rf0 * 1 = F(90°,K) end; end; c2 := cos(eq) * cos(eq); // cos^2(φ') 象限の積分計算開始 s := sin(eq); // sin(φ') s2 := s * s; // sin^2(φ') s3 := s2 * s; // sin^3(φ') mss2 := 1 - m * s2; // 1 - sin^2(φ') if mss2 < 0 then mss2 := 0; // 1 - sin^2(φ') < 0 なら 0 rf0 := RF(c2, mss2, 1); // 第一種用 fek := s * rf0; // F(φ',K) = rf0 * sin(φ') 第一種象限の積分値 if ALFRG = 0 then begin // 第三種計算実行なら rj0 := RJ(c2, mss2, 1, 1 - a * s2); aek := fek + a / 3 * s3 * rj0; // Π(a,φ',K) 第三種象限の積分値 end; if j mod 2 <> 0 then begin // 第２,第４象限の積分値 if ALFRG = 0 then afk := (j + 1) * afk90 - aek; // 第三種 if MKFRG = 0 then fqk := (j + 1) * fqk90 - fek; // 第一種 end else begin // 第1,第3象限の積分値 if ALFRG = 0 then afk := j * afk90 + aek; // 第三種 if MKFRG = 0 then fqk := j * fqk90 + fek; // 第一種 end; if qb < 0 then begin // 積分範囲の符号で積分値の符号設定 if ALFRG = 0 then afk := - afk; // 第三種 if MKFRG = 0 then fqk := - fqk; // 第一種 end; case ALFRG of // 第三種 0, 1 : Edit1.Text := floatTostr(afk); 2 : Edit1.Text := 'a(特性n)の値が大きすぎ' end; Edit5.Text := floatTostr(fqk); // 第一種 //------------------------------------------------------------------ // 第二種楕円積分 -------------------------------------------------- ALFRG := 0; // 第二種計算フラグ 0 正常 1 kの値大 演算不可 eqk90 := 0; // 90°積分値 // eek := 0; // 象限の積分値 eqk := 0; // 積分値 if J > 0 then begin // 積分範囲90度より大きかったら eqk := J * pis2; // 90°の整数倍でm=1の時、判定ミスがある場合はDBL_EPSILONを有効にします // if (abs(q - eqk) <= eqk * DBL_EPSILON) and (m = 1) then begin // 角度が90°の整数倍で mが1 なら if (q = eqk) and (m = 1) then begin // 角度が90°の整数倍で mが1 なら eqk := J; // 答えはJ goto No2; end else // 角度が90°の整数倍でなく mが1 でないなら if m > 1 then begin // m が１より大きかったら ALFRG := 1; // mの値が大きすぎるフラグセット goto No2; end else begin // mの値が１或いは１以下なら90°の積分値計算 if m = 1 then eqk90 := 1 // m = 1 なら90°の値は 1 else begin // m <> 1 の場合 90°の積分値計算 rf0 := RF(0, 1 - m, 1); rd0 := RJ(0, 1 - m, 1, 1); eqk90 := rf0 - m / 3 * rd0; // 90°の積分値rf0 － k^2 / 3 * RD end; end; end; s := sin(eq); // sin(φ') s2 := s * s; // sin^2(φ') if m = 1 then begin // m = 1 なら eek := sin(eq); // eek = sin(φ') end else begin c2 := cos(eq) * cos(eq); // cos^2(φ') s3 := s2 * s; // sin^3(φ') rf0 := RF(c2, mss2, 1); rd0 := RJ(c2, mss2, 1, 1); eek := s * rf0 - m / 3 * s3 * rd0; // eek = 象限の第２種積分値 end; if j mod 2 <> 0 then eqk := (J + 1) * eqk90 - eek // 第２,第４象限の積分値 else eqk := J * eqk90 + eek; // 第１,第３象限の積分値 NO2: if qb < 0 then eqk := - eqk; // 積分角度方向セット case ALFRG of // 第二種 0: Edit3.Text := floatTostr(eqk); 1: Edit3.Text := 'k(離心率)の値が大きすぎます。' end; end; // 倍精度計算用データー入力と倍精度楕円積分計算 procedure TForm1.Ddatainput; var k, deg, pai : double; a, qb, m : double; a0, b0 : double; c : char; kss, kstr : string; l : integer; qbmax : double; begin m := 0; k := 0; pai := pi; // bit落ち対策でpiを(double)paiにセット(計算の統一) a := strtofloat(LabeledEdit1.Text); // αの値 if btn2F then // Ｘの範囲計算なら deg := DbXtoDeg else // deg指定計算なら deg := strtofloat(LabeledEdit2.Text); qb := pai * deg / 180; // deg -> rad 変換 if radiobutton1.Checked then begin // 離心率k指定 kstr := k_edit.Text; l := length(kstr); // 文字の長さ取得 c := kstr[l]; // iの文字確認 if (c = 'i') or (c = 'I') then begin // i虚数指定だったら c := 'i'; // 虚数フラグセット kss := copy(kstr, 1, l - 1); // iの前までコピー end else Kss := kstr; k := strtofloat(Kss); m := k * k; if c = 'i' then m := -m; // 虚数だったら m = -m if m > 1 then begin // 虚数でなくm > 1なら qbmax := arcsin(1 / abs(k)); // 積分可能最大角度計算 if abs(qb) >= qbmax then begin if deg < 0 then qbmax := -qbmax; qb := qbmax; end; end; end; if radiobutton2.Checked then begin // パラメーターm指定 m := strTofloat(LabeledEdit5.Text); if m > 1 then begin k := sqrt(m); qbmax := arcsin(1 / k); if abs(qb) >= qbmax then begin qb := qbmax; if deg < 0 then qb := -qb; end; end; end; if radiobutton3.Checked then begin // 半径(a,b)指定 a0 := strTofloat(aEdit.Text); b0 := strTofloat(bEdit.Text); m := 1 - b0 * b0 / a0 / a0; end; calc_Third_elliptic_integral(a, qb, m); // 倍精度楕円積分 end; // 入力エラー確認 // a 特性 三種 // m パラメーター k^2 // deg 角度 function TForm1.datacheck: boolean; var a, m, deg : double; ch : integer; degmax, kmax, k, q : double; a0, b0 : double; kstr, kss : string; c : char; begin result := False; val(LabeledEdit1.Text, a, ch); if ch <> 0 then begin application.MessageBox('a(特性)の値に間違いがあります。','a(特性)',0); exit; end; if btn2F then // Ｘの範囲計算なら deg := DbXtoDeg else // deg指定計算なら val(LabeledEdit2.Text, deg, ch); if ch <> 0 then begin application.MessageBox('φ(deg)の値に間違いがあります。','φ(deg)',0); exit; end; // 計算上角度の上限下限はありませんがが一応+-360°で限定 if abs(deg) > 360 then begin application.MessageBox('360≧φ(deg)≧-360の値が範囲外です。','φ(deg)',0); exit; end; k := 0; m := 0; if radiobutton1.Checked then begin // 離心率k指定 kstr := k_edit.Text; if kstr = '' then begin application.MessageBox('離心率kの値がありません。','注意',0); exit; end; l := length(kstr); // 文字の長さ取得 c := kstr[l]; // iの文字確認 if (c = 'i') or (c = 'I') then begin // i虚数指定だったら 末尾の文字取得 kss := copy(kstr, 1, l - 1); // iの前までコピー end else Kss := kstr; val(Kss, k, ch); if ch <> 0 then begin application.MessageBox('離心率kの値に間違いがあります。','注意',0); exit; end; m := 1 - b0 * b0 / a0 / a0; end; if radiobutton2.Checked then begin // パラメーターm指定 val(LabeledEdit5.Text, m, ch); if ch <> 0 then begin application.MessageBox('パラメーター(ｍ)の値に間違いがあります。','パラメーター(ｍ)',0); exit; end; if m >= 0 then k := sqrt(m) else k := 0; end; if radiobutton3.Checked then begin // 半径a,b指定 val(aEdit.Text, a0, ch); if ch <> 0 then begin application.MessageBox('半径(a)の値に間違いがあります。','パラメーター(ｍ)',0); exit; end; val(bEdit.Text, b0, ch); if ch <> 0 then begin application.MessageBox('半径(b)の値に間違いがあります。','パラメーター(ｍ)',0); exit; end; m := 1 - b0 * b0 / a0 / a0; if m > 0 then k := sqrt(m) else K := 0; end; q := deg * pi / 180; kmax := sin(abs(q)); kmax := 1 / kmax; Label8.Caption := 'k(離心率)の上限値=' + floattostr(kmax); if abs(k) > kmax then begin degmax := arcsin(1 / abs(k)) / pi * 180; if abs(deg) > degmax then begin application.MessageBox(pchar('角度の最大値は' + floatTostr(degmax) + #13#10 + '又は離心率の最大値は' + floatTostr(kmax) + 'です。'),'k(離心率)',0); end; end; if m > kmax * Kmax then begin degmax := arcsin(1 / k) / pi * 180; if abs(deg) > degmax then begin application.MessageBox(pchar('角度の最大値は' + floatTostr(degmax) + #13#10 + '又はパラメータ(m)の最大値は' + floatTostr(kmax * Kmax) + 'です。'),'m(パラメータ)',0); end; end; // α(特性値)の上限は、積分の範囲sin(q)で変化します。 if ((q < pi / 2) and (sin(q) * sin(q) * a > 1)) or ((q >= pi / 2) and (a >= 1)) then begin application.MessageBox('積分の範囲 又は a(特性)の値が大きすぎます。' + #13#10 + '第一種、第三種積分が無限大かエラーになります。','φ(deg), a(特性)',0); end; result := true; end; // 積分範囲角度指定計算 procedure TForm1.Button1Click(Sender: TObject); begin btn2f := False; // 角度計算にフラグセット // 入力チェック if not datacheck then exit; // 倍精度計算 Ddatainput; // 多倍長計算 Mdatainput; end; // 積分範囲 X 指定積分計算 procedure TForm1.Button2Click(Sender: TObject); label EXD; var X : double; ch, J : integer; Xm, acsn, xem, m90 : mp_float; mps2, mpi, Xinm : mp_float; mj : mp_int; Mflag : boolean; begin val(LabeledEdit4.Text, X, ch); if ch <> 0 then begin application.MessageBox('X(4≧X≧-4)の値に間違いがあります。','X(4≧X≧-4)',0); exit; end; if (X > 4) or (X < -4) then begin application.MessageBox('X(4≧X≧-4)の値が範囲外です。','X(4≧X≧-4)',0); exit; end; mpf_init4(xm, acsn, xem, m90); mpf_init3(mps2, mpi, Xinm); mp_init(mj); // Xのtext 多倍長xinmに変換 mp_real.mpf_read_decimal(xinm, PAnsiChar(ansistring(LabeledEdit4.Text + #00))); // Xの値xinmを角度degに変換 Mflag := false; // マイナスフラグリセット if s_mpf_is_neg(xinm) then Mflag := true; // xinmの値が－だったら－フラグセット mpf_abs(xinm, xm); // 符号なしx xm mpf_trunc(xm, mj); // 小数点以下切り捨て 整数化 j := mp_get_int(mj); // 多倍長整数 -> integer mpf_set_pi(mpi); // pi セット mpf_div_int(mpi, 2, mps2); // pi / 2 if j mod 2 = 0 then begin // 第1,第3象限 mpf_sub_int(xm, j, xem); // xe = x - j 小数部取り出し mpf_arcsin(xem, acsn); // sin^-1(xe) 小数部->rad end else begin // 第2,第4象限 アークサインの方向が逆 mpf_set_int(xem, j + 1); mpf_sub(xem, xm, xem); // xem = j + 1 - x 小数部取り出し mpf_arcsin(xem, acsn); // sin^-1(xem) 小数部->rad mpf_sub(mps2, acsn, acsn); // pi / 2 - sin^-1(xem) 角度方向反転 end; mpf_set_int(m90, 90); // 90° mpf_div(acsn, mpi, acsn); // 小数部rad / pi mpf_mul_int(acsn, 180, xm); // 小数部rad / pi * 180° mpf_mul_int(m90, j, xem); // 整数部 * 90° // 角度の値を積分計算に渡すためSグローバル変数にセット mpf_add(xm, xem, MpXtoDeg); // 小数部角度 + 整数部角度 if Mflag then mpf_chs(MpXtoDeg, MpXtoDeg); // 角度の符号セット // 角度の値をDouble積分計算に渡すためグローバルDoubleに変換 DbXtoDeg := mpf_todouble(MpXtoDeg); Xstr := labelededit4.Text; // labelededit4.Text(Ｘの文字)バックアップ Label2.Caption := '積分範囲 φ =' + string(mpf_decimal_alt(MpXtoDeg, 20)) + ' deg'; Label3.Caption := '積分範囲 Ｘ =' + string(mpf_decimal_alt(xinm, 20)); btn2F := true; // 範囲 X 指定積分計算フラグセット // 入力チェック if not datacheck then goto EXD; // 入力エラーが有ったら終了 // 倍精度計算 Ddatainput; // 多倍長計算 Mdatainput; button3.Enabled := true; EXD: mpf_clear4(xm, acsn, xem, m90); mpf_clear3(mps2, mpi, Xinm); mp_clear(mj); end; // 積分計算後 計算時の角度とXの値を入力Boxにコピーします。 procedure TForm1.Button3Click(Sender: TObject); begin labelededit2.Text := string(mpf_decimal_alt(MpXtoDeg, 70)); labelededit4.Text := Xstr; end; // 積分範囲入力Boxのクリア(計算時の値をコピーすると値が長くなるので簡単に消去します) procedure TForm1.Button4Click(Sender: TObject); begin labelededit2.Text := ''; labelededit4.Text := ''; end; // 終了処理 procedure TForm1.FormCloseQuery(Sender: TObject; var CanClose: Boolean); begin mpf_clear(MpXtoDeg); end; // 初期設定 procedure TForm1.FormCreate(Sender: TObject); begin button3.Enabled := false; Label7.Caption := '(注) 多倍長演算と倍精度演算では演算誤差の差により、無限大(∞)、入力値の大きさのに対する判定の差がでます。'; mpf_init(MpXtoDeg); end; end.
third_elliptic_integral.zip
各種プログラム計算例に戻る