理論的には誤差は無いはずですが、実際の計算は、有効桁数が限られているので、実際にプログラムを組み確認をしました。
α は角度、k は離心率です。
k = √(1-b2/a2) a = 長半径、b = 短半径
k2 = 1-b2/a2
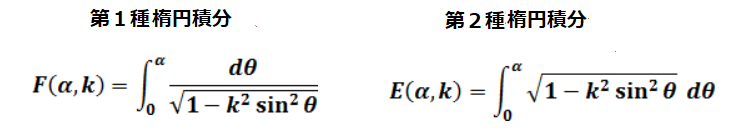
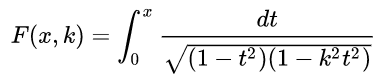
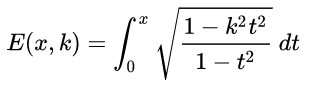
2020/12/12 ランデン変換による計算の検討追加
計算方法によっては、90°分割計算を行なわなくても、大きな角度の第１種、第２種積分が出来る計算があるので追加しました。
2018/05/07 第一種不完全積分 値表示追加
楕円の周長、楕円弧長の計算時使用する楕円積分の計算時の誤差の確認
楕円の周長、楕円弧長、楕円体の体積を計算する時の楕円積分の計算誤差について確認をします。
理論的には誤差は無いはずですが、実際の計算は、有効桁数が限られているので、実際にプログラムを組み確認をしました。
α は角度、k は離心率です。
k = √(1-b2/a2) a = 長半径、b = 短半径
k2 = 1-b2/a2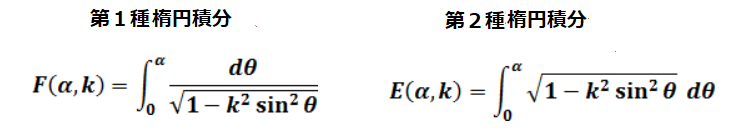
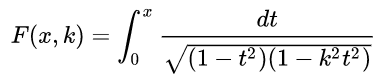
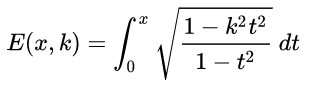
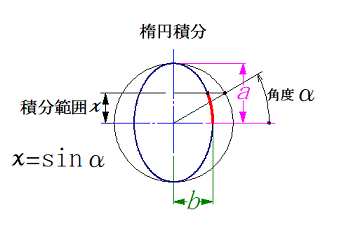
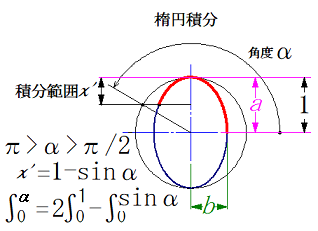
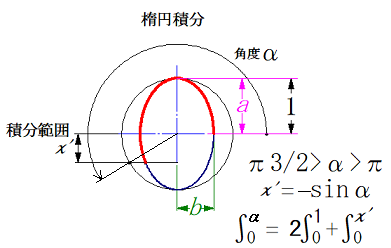
楕円積分はランデン変換を使用しています。
ランデン変換に関しては、インターネットで検索して参照して下さい。
新しく検討したプログラムは、Mathematics Source Library C & ASM にある第１、２種の楕円積分をDelphiに変換したものです。
k = 1 時以外は、制限なく計算が出来ますし、90°を越えた場合90°分割をしなくても分割した場合と、同じ結果を得ることができます。
(元のプログラムは、90°分割していましたが、分割無しをテストして結果、分割無しでも同じ計算結果を得ることができました。)
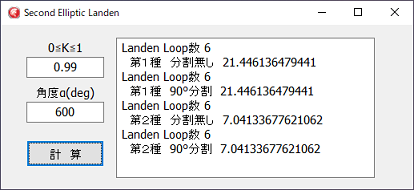左図は、600°の積分でも、90°分割無しでも分割した場合と同じ計算結果が出ている例です。
kの値が、0.999・・・と１に近づくほど誤差が大きくなるのは、計算の精度上、他のプログラムと同じです。
多倍長の計算を使用すれば、精度が高くなりますが、多倍長のプログラムは省略しています。
(必要であれば、第一、二、三種楕円積分)を参照して下さい。
プログラム
ランデン変換ルーチンは第１種、第２種両方同時に計算されます。
ルジャンドルの楕円積分です。
parameter = m = k2
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
BitBtn1: TBitBtn;
Memo1: TMemo;
procedure FormCreate(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses system.Math;
var
LDBL_EPSILON: extended;
function Landen_Transform(phi, parameter: extended; var F, Fk, E, Ek: extended): integer;
var
two_n: extended;
a, g, a_old, g_old: extended;
tan_2n_phi, sum, integral: extended;
n : integer;
begin
two_n := 1.0;
a := 1.0;
g := sqrt(1.0 - parameter);
sum := 2.0 * (2.0 - parameter);
integral := 0.0;
n := 0;
repeat
tan_2n_phi := tan(two_n * phi);
sum := sum - two_n * (a - g) * (a - g);
two_n := two_n + two_n;
phi := phi - arctan((a - g) * tan_2n_phi / (a + g * tan_2n_phi * tan_2n_phi)) / two_n;
integral := integral + (a - g) * sin(two_n * phi);
g_old := g;
a_old := a;
a := 1 / 2 * (g_old + a_old);
g := sqrt(g_old * a_old);
inc(n);
until (abs(a_old - g_old) <= (a_old * LDBL_EPSILON));
F := phi / g;
Fk := PI / 2 / g;
E := 1 / 2 * integral + 1 / 4 * sum * phi / g;
Ek := PI / 8 / a * sum;
result := n;
end;
procedure Elliptic_Integral_Second_Kind(phi, m: extended; var E, Ek: extended);
var
F, Fk: extended;
n, i: integer;
begin
if m = 1 then begin
if (abs(phi) <= PI / 2) then begin
E := sin(phi);
exit;
end;
n := trunc((abs(phi) + PI / 2) / PI);
E := n + n + sin(abs(phi) - n * PI);
if phi < 0 then E := - E;
exit;
end;
// 分割無し計算
i := Landen_Transform(abs(phi), m, F, Fk, E, Ek);
Form1.Memo1.Lines.Append('Landen Loop数 ' + intTostr(i));
E := sign(phi) * E;
Form1.Memo1.Lines.Append(' 第２種 分割無し ' + floatTostr(E));
// 90°分割計算
n := trunc((phi + PI / 2) / PI );
phi := phi - n * PI;
n := n + n;
i := Landen_Transform(abs(phi), m, F, Fk, E, Ek);
Form1.Memo1.Lines.Append('Landen Loop数 ' + intTostr(i));
E := sign(phi) * E + n * Ek;
end;
procedure Elliptic_Integral_First_Kind(phi, m: extended; var F, K: extended);
var
E, Ek: extended;
n, i: integer;
begin
if m = 1.0 then begin
if abs(phi) >= PI / 2 then begin
F := infinity;
if phi < 0 then F := -F;
exit;
end;
Ek := tan(Phi);
F := sign(Phi) * ln(abs(Ek) + sqrt(1.0 + Ek * Ek));
exit;
end;
// 分割無し計算
i := Landen_Transform(abs(phi), m, F, K, E, Ek);
Form1.Memo1.Lines.Append('Landen Loop数 ' + intTostr(i));
F := sign(phi) * F;
Form1.Memo1.Lines.Append(' 第１種 分割無し ' + floatTostr(F));
// 90°分割計算
n := trunc((phi + PI / 2) / PI);
phi := phi - n * PI;
n := n + n;
i := Landen_Transform(abs(phi), m, F, K, E, Ek);
Form1.Memo1.Lines.Append('Landen Loop数 ' + intTostr(i));
F := sign(phi) * F + n * K;
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
var
F, K, E, Ek: extended;
kin, m : extended;
deg, phi: extended;
ch: integer;
begin
val(labelededit1.Text, kin, ch);
if ch <> 0 then begin
application.MessageBox('離心率kの値に間違いがあります。','注意',0);
exit;
end;
if (kin < 0) or (kin > 1) then begin
application.MessageBox('離心率kの値が範囲外です。','注意',0);
exit;
end;
val(labelededit2.Text, deg, ch);
if ch <> 0 then begin
application.MessageBox('積分の範囲αの値に間違いがあります。','注意',0);
exit;
end;
memo1.Clear;
m := kin * kin; // k^2
phi := deg / 180 * pi;
Elliptic_Integral_First_Kind(phi, m, F, K);
Memo1.Lines.Append(' 第１種 90°分割 ' + floatTostr(F));
Elliptic_Integral_Second_Kind(phi, m, E, Ek);
Memo1.Lines.Append(' 第２種 90°分割 ' + floatTostr(E));
end;
procedure TForm1.FormCreate(Sender: TObject);
var
one, tmp: extended;
begin
one := 1;
LDBL_EPSILON := one;
repeat
LDBL_EPSILON := LDBL_EPSILON / 2;
tmp := LDBL_EPSILON + one;
until tmp = one;
LDBL_EPSILON := LDBL_EPSILON * 2;
memo1.Clear;
memo1.Lines.Append('第１種、第２種楕円積分');
end;
end.
完全楕円積分を含むプログラム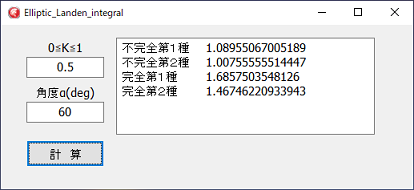
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
BitBtn1: TBitBtn;
Memo1: TMemo;
procedure FormCreate(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses system.Math;
var
LDBL_EPSILON: extended;
//==================================================================================================
// 第１種完全楕円積分
function Complete_Elliptic_Integral_First_Kind(parameter: extended): extended;
var
a, g, a_old, g_old: extended;
begin
if parameter = 0 then begin
result := PI / 2;
exit;
end;
if parameter = 1 then begin
result := infinity;
exit;;
end;
a := 1;
g := sqrt(1.0 - parameter);
while true do begin
g_old := g;
a_old := a;
a := 1 / 2 * (g_old + a_old);
g := sqrt(g_old * a_old);
if abs(a_old - g_old) <= a_old * LDBL_EPSILON then break;
end;
result := PI / 2 / g;
end;
// 第２種完全楕円積分
function Complete_Elliptic_Integral_Second_Kind(parameter: extended): extended;
var
a, g, a_old, g_old: extended;
two_n: extended;
Ek: extended;
begin
if parameter = 0 then begin
result := PI / 2;
exit;
end;
if parameter = 1 then begin
result := 1;
exit;
end;
a := 1;
g := sqrt(1 - parameter);
two_n := 1;
Ek := 2 - parameter;
while true do begin
g_old := g;
a_old := a;
a := (g_old + a_old) / 2;
g := a_old * g_old;
two_n := two_n + two_n;
Ek := Ek - two_n * (a * a - g);
if abs(a_old - g_old) <= (a_old * LDBL_EPSILON) then break;
g := sqrt(g);
end;
result := (PI / 4 / a) * Ek;
end;
//==================================================================================================
// 第１、２種ランデン変換
procedure Landen_Transform(phi, parameter: extended; var F, Fk, E, Ek: extended);
var
two_n: extended;
a, g, a_old, g_old: extended;
tan_2n_phi, sum, integral: extended;
begin
two_n := 1.0;
a := 1.0;
g := sqrt(1.0 - parameter);
sum := 2.0 * (2.0 - parameter);
integral := 0.0;
repeat
tan_2n_phi := tan(two_n * phi);
sum := sum - two_n * (a - g) * (a - g);
two_n := two_n + two_n;
phi := phi - arctan((a - g) * tan_2n_phi / (a + g * tan_2n_phi * tan_2n_phi)) / two_n;
integral := integral + (a - g) * sin(two_n * phi);
g_old := g;
a_old := a;
a := (g_old + a_old) / 2;
g := sqrt(g_old * a_old);
until (abs(a_old - g_old) <= (a_old * LDBL_EPSILON));
F := phi / g;
Fk := PI / 2 / g;
E := integral / 2 + sum * phi / g / 4;
Ek := PI / 8 / a * sum;
end;
// 第２種不完全楕円積分
procedure Elliptic_Integral_Second_Kind(phi, m: extended; var E, Ek: extended);
var
F, Fk: extended;
n: integer;
begin
if m = 1 then begin
if (abs(phi) <= PI / 2) then begin
E := sin(phi);
exit;
end;
n := trunc((abs(phi) + PI / 2) / PI);
E := n + n + sin(abs(phi) - n * PI);
if phi < 0 then E := - E;
exit;
end;
n := trunc((phi + PI / 2) / PI );
phi := phi - n * PI;
n := n + n;
Landen_Transform(abs(phi), m, F, Fk, E, Ek);
E := sign(phi) * E + n * Ek;
end;
// 第１種不完全楕円積分
procedure Elliptic_Integral_First_Kind(phi, m: extended; var F, K: extended);
var
E, Ek: extended;
n : integer;
begin
if m = 1.0 then begin
if abs(phi) >= PI / 2 then begin
F := infinity;
if phi < 0 then F := -F;
exit;
end;
Ek := tan(Phi);
F := sign(Phi) * ln(abs(Ek) + sqrt(1.0 + Ek * Ek));
exit;
end;
n := trunc((phi + PI / 2) / PI);
phi := phi - n * PI;
n := n + n;
Landen_Transform(abs(phi), m, F, K, E, Ek);
F := sign(phi) * F + n * K;
end;
//==================================================================================================
procedure TForm1.BitBtn1Click(Sender: TObject);
var
F, K, E, Ek: extended;
kin, m : extended;
deg, phi: extended;
ch: integer;
begin
val(labelededit1.Text, kin, ch);
if ch <> 0 then begin
application.MessageBox('離心率kの値に間違いがあります。','注意',0);
exit;
end;
if (kin < 0) or (kin > 1) then begin
application.MessageBox('離心率kの値が範囲外です。','注意',0);
exit;
end;
val(labelededit2.Text, deg, ch);
if ch <> 0 then begin
application.MessageBox('積分の範囲αの値に間違いがあります。','注意',0);
exit;
end;
memo1.Clear;
m := kin * kin; // k^2
phi := deg / 180 * pi;
Elliptic_Integral_First_Kind(phi, m, F, K);
Memo1.Lines.Append('不完全第１種 ' + floatTostr(F));
Elliptic_Integral_Second_Kind(phi, m, E, Ek);
Memo1.Lines.Append('不完全第２種 ' + floatTostr(E));
K := Complete_Elliptic_Integral_First_Kind(m);
Memo1.Lines.Append('完全第１種 ' + floatTostr(K));
EK := Complete_Elliptic_Integral_Second_Kind(m);
Memo1.Lines.Append('完全第２種 ' + floatTostr(EK));
end;
procedure TForm1.FormCreate(Sender: TObject);
var
one, tmp: extended;
begin
one := 1;
LDBL_EPSILON := one;
repeat
LDBL_EPSILON := LDBL_EPSILON / 2;
tmp := LDBL_EPSILON + one;
until tmp = one;
LDBL_EPSILON := LDBL_EPSILON * 2;
memo1.Clear;
memo1.Lines.Append('第１種、第２種楕円積分');
end;
end.
以前のプログラムについて
F(α,K)、E(α,K)の公式は、α
の値が90°を超えても良いような公式ですが、ランデン変換した場合の計算は、k = 1 の時 α < 90 °、 0<k <1 の時 α <= 90°から360°程度、k = 0時は計算不可となります。
k の値が１より小さい場合、90°を超えても、演算エラーにならずに答えが出る場合がありますが、誤差が出ます。
k の値が小さいほど、大きな角度まで、エラーが出ずに計算は可能ですが誤差も大きくなります。
F(x,K)、E(x,K)の場合は、xの値が １ (sin90°)を超えることは出来ません。
下記の最初の表は、最大角度を360°に設定して、計算した場合です。
360°以下の値は、その値を超えると演算エラーとなり計算できない事を表しています。
K=1の時の90°の値は、ランデン変換は使用していません、90°以下はランデン変換となります。
Kの値が、0.9以下になると、360°迄位は、実用上問題ない誤差となつていますが、出来れば、90°迄の値で使用した方が誤差の無い計算が出来ます。
下記の最初の表は、浮動小数点計算精度Double(8バイト)で計算した場合で、次の表は多倍長演算をした場合です。
有効桁数が増えれば、誤差は小さくなります。
現実的ではありませんが、非常に有効桁数が大きい場合、Kの値が１より小さければ、角度が90°を超えても、精度の高い計算結果を得ることが出来る事になります。
(誤差の値は、90°(象限)分割して計算した場合との差を表しています。)
Double(8バイト)
K 角度 誤差 1 90 0 0.9999999999 180 6.45985486545613E-08 0.999999999 180 7.61114785115606E-07 0.99999999 180 8.76243974099025E-06 0.9999999 360 4.0748193308669E-06 0.999999 360 0.000155876382432 0.99999 360 0.002709905994357 0.9999 360 0.038594957185574 0.999 360 0.00026047716584 0.99 360 5.06253291218826E-07 0.9 360 2.57824054676367E-10 0.8 360 5.4278152404311E-12 0.7 360 3.4887406305321E-11 0.6 360 1.03343315226882E-12 0.5 360 1.5585133410402E-12 0.4 360 6.92994757952237E-13 0.3 360 6.2208169355063E-13 0.2 360 2.85593693147796E-14 0.1 360 7.08564676216894E-14
多倍長演算で計算した場合 積分角 640°です。
上記の表より大きな角度を指定していますが、誤差は小さくなっています。
K 角度 誤差 1 90 0 0.9999999999 640 7.68E-13 0.999999999 640 7.68E-12 0.99999999 640 1.20E-14 0.9999999 640 -8.12E-20 0.999999 640 -1.39E-26 0.99999 640 -9.07E-35 0.9999 640 4.07E-41 0.999 640 -1.26E-47 0.99 640 -2.74E-54 0.9 640 -6.40E-61 0.8 640 -1.09E-63 0.7 640 -9.77E-65 0.6 640 -4.24E-66 0.5 640 -3.15E-66 0.4 640 -8.61E-67 0.3 640 -9.40E-68 0.2 640 1.02E-68 0.1 640 -5.58E-69
プログラム ランデン変換第一二種楕円積分計算
//---------------------------------------------------------------------- // 第１種第２種楕円積分 // FBnKn[0] 第１種楕円積分解 // EBnKn[0] 第２種楕円積分解 // ランデン変換 // Q 角度 deg // K 離心率 // 精度Extended の指定でも、64ビットでコンパイルするとdoubleになります。 //---------------------------------------------------------------------- function TForm1.second_imperfect_elliptic_integral(Q, K: Extended: var EBnKnAns, FBnKnAns: Extended): boolean; var I, MI : integer; Kn : array of Extended; // Kn knd : array of Extended; // k'n N2SKn : array of Extended; // 2/(1+Kn) T2SKnd : array of Extended; // П2/(1+Kn') BRad : array of Extended; // β(rad) SinBn : array of Extended; // sinβn FBnKn : array of Extended; // F(βn,kn) EBnKn : array of Extended; // E(βn,kn) LnD, nD : Extended; begin result := true; // 配列の設定 // K[n] = 2 * sqrt(K[n-1])/(1+k[n-1]) の計算し、同じ値"1"が出るまでくりかえしましその時のn(配列の大きさ)の値を求めます。 // "1"の値は、近似1で本来の1ではありません。 // 演算上のビット落ちによりいくら繰り返しても、同じビット落ちを繰り返すので注意が必要です。 // LnD = 1 での判定は使用できません // デバッグ上の表示は"1" でも最終ビット付近に誤差があります MI := 0; LnD := K; repeat inc(MI); nD := LnD; LnD := 2 * sqrt(nD) / (1 + nD); until LnD = nD; setlength(Kn, MI); // Kn setlength(knd, MI); // k'n setlength(N2SKn, MI); // 2/(1+Kn) setlength(T2SKnd, MI); // П2/(1+Kn') setlength(BRad, MI); // β(rad) setlength(SinBn, MI); // sinβn setlength(FBnKn, MI); // F(βn,kn) setlength(EBnKn, MI); // E(βn,kn) dec(MI); // K = 0 の時は円なのでpiの角度値rad。 // k = 0 の計算はランデン変換では出来ません。 if K = 0 then begin EBnKnAns := pi * Q / 180; exit; end; // K = 1 の時は、bの半径が0で楕円ではなく直線となります。 // K = 1 で Q=90 の時 ランデン変換では計算できません。 // bの値が0に近いが0でないときにもKの値がビット落ちで1になります。 // この時にエラーが発生して計算が中断されない様にします。 // 微小角分割積分計算ではエラーになりません。 if K = 1 then begin if abs(Q) = 90 then begin if Q > 0 then EBnKnAns := 1 else EBnKnAns := -1; exit; end; if abs(Q) > 90 then begin result := false; // 演算エラー設定 exit; end; end; // 1 > K > 0 又は K = 1 and abs(Q) < 90 の範囲にある時ランデン変換による楕円積分積分をおこないます。 // Q角度の値が90°を超えて大きい場合、誤差が大きくなると同時に、自然対数変換の演算エラーが発生します。 kn[0] := K; // 離心率Kの値設定 for I := 1 to MI do kn[I] := 2 * sqrt(Kn[I - 1])/(1 + Kn[I - 1]); knd[0] := 1; for I := 1 to MI do knd[I] := (1 - kn[I - 1]) / (1 + Kn[I - 1]); for I := 0 to MI do N2SKn[I] := 2 / (1 + kn[I]); T2SKnd[MI] := N2SKn[MI]; for I := MI - 1 downto 0 do T2SKnd[I] := T2SKnd[I + 1] * N2SKn[I]; BRad[0] := Q / 180 * pi; // 角度Qの値設定 for I := 1 to MI do BRad[I] := (arcsin(kn[I - 1] * sin(Brad[I - 1])) + Brad[I - 1]) / 2; for I := 0 to MI do SinBn[I] := sin(Brad[I]); nD := (1 + sin(Brad[MI])) / cos(Brad[MI]); // nd が ０より大きくないと自然対数に変換できません。 if nD <= 0 then begin result := false; // 演算エラー設定 exit; end; LnD := LN(nD); for I := 0 to MI do FBnKn[I] := T2SKnd[I] * LnD; // FBnKn[0] 第１種楕円積分値 EBnKn[MI] := sin(Brad[MI]); for I := MI - 1 downto 0 do EBnKn[I] := (2 * EBnKn[I + 1] + 2 * knd[I + 1] * FBnKn[I + 1]) / (1 + knd[I + 1]) - kn[I] * SinBn[I]; EBnKnAns := EBnKn[0]; // EBnKn[0] 第２種楕円積分値 FBnKnAns := FBnKn[0]; end;
配列の大きさの設定
ランデン変換の計算で注意が必要なのは、ランデン変換の最初の計算です。
次の計算で、kn[0],kn[1],kn[2],kn[3]・・・の値が 1 に近似するまで繰り返すのですが
kn[0] := K;
for I := 1 to MI do
kn[I] := 2 * sqrt(Kn[I - 1])/(1 + Kn[I - 1]);
計算結果が
0.9, 0.99, 0.995, 0.999, ・,・,・,1,1,1,1,の様になる場合
配列の大きさを最後の配列の値が近似 １ になる様にすると計算精度が高くなります。
0.9, 0.99, 0.995, 0.999, ・,・,・,1
配列の大きさをMI、LnDの初期設定値をK (離心率)とすると
MI := 0; // 配列の大きさ
LnD := K; // 離心率
repeat
inc(MI);
nD := LnD;
LnD := 2 * sqrt(nD) / (1 + nD);
until LnD = nD;
LNDとnDの値が同じ値になるまで、繰り返して、必要な配列の大きさ MI を計算します。
値は１に近くなるのですが、実際には演算の桁落ちにより、同じ値になります。
repeat でなくて while 文でも if 文でも構いません。
if 文の場合は、Label と goto Label が必要となります。
配列の最後の値が 1 に近い値になるのですが、LnD = 1 で判定すると、デバッグ上 "1" と表示されても、浮動小数点のビット落ちの関係で、LnD の値が本当の 1 になっていない場合があり、閉ループとなってしまう場合があります。
有効桁数が多い程、配列の大きさは、大きくなります。
ランデン変換の精度
積分角度Qの値が 90°を超えても、積分の計算が出来る場合もありますが、誤差が大きくなるので、90°(象限)毎に分割して計算して、誤差が大きくならないようにします。
角度を90°で除算して、整数部と、余りの部分にわけ、余りの部分の角度について積分を行い、90°の積分値を整数倍して、加算して指定角度の積分値とします。
上の方の図にある様に、計算する象限によって、計算方法を変更する必要があります。
奇数象限 １, ３ と 偶数象限 ２，４ が同じ計算となります。
Q 積分角
I := Trunc(Q / 90); // 90°で除算して整数部の取得
Qd 余り部分角度
D90 90°積分値
S 余り部分の積分値
SQD 角度Qの積分値
象限によって余り部分の積分角度計算方法選択
if I mod 2 = 0 then Qd := Q - I * 90 奇数象限
else Qd := (I + 1) * 90 - Q; 偶数象限
D90 = elliptic_integera(90);
S = elliptic_integera(Qd);
象限によって余り部分の積分計算方法選択
if I mod 2 = 0 then SDQ := I * D90 + S
else SDQ := (I + 1) * D90 - S;
前記計算は、短軸基準ですが、長軸基準にする場合 奇数象限と偶数象限を入れ替えるだけです。
90°象限毎に分割して計算した場合の計算誤差は、８バイト演算の場合、浮動小数点で表示される最後の桁の値が正解と異なるぐらいの正確さです。
多倍長演算時は、50桁までしか確認していませんが、70桁程度の有効桁数があるので、50桁正しい値を表示します。
微小角分割積分
微小角分割による積分は、ランデン変換による積分にプログラム上の間違いが無いか確認の為にプログラムの中に組み込んでいます。
分割数は、１°を１００００分割していますので、結構高い精度で計算されます。
微小角分割積分の場合、プログラムが単純なので、バグの可能性が小さくなり、この値と大差がなければ、ランデン変換のプログラムにもミスが無いと言えます。
多倍長演算での微小角分割積分のプログラムは組み込んでいますせん。
可成り小さい角度に分割できますが、余りにも計算時間が掛かりすぎます。
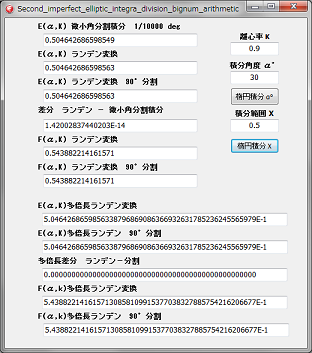第一種楕円積分の値と、第二種楕円積分の値が計算表示されます。
積分の範囲は、角度と、Xの値で指定ができます。
:計算は、角度でπに変換して行われます。(α=sin-1X)
第一種楕円積分の微小角分割積分に関しては、此処のプログラムには組み込んでいません。
第一種楕円積分の微小角分割積分の場合、k(離芯率)の値と、積分の範囲が90°に近くなるにつれ、分母の値が小さくなるので、誤差が大きくなります。
精度確認プログラム全体
//----------------------------------------------------- // 第一種、第二種楕円積分の確認プログラム // ランデン変換ではKの値 1>K>0 の範囲となりますので // K = 1 と K =0 の場合について別途追加しています。 // 多倍長演算にMPArithを使用しています。 // uses に mp_types, mp_real の追加が必要です。 // MPArith については下記を参照してください。 // "https://web.archive.org/web/20181215233944/http://wolfgang-ehrhardt.de/mp_intro.html" //----------------------------------------------------- unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, mp_types, mp_real; type TForm1 = class(TForm) Button1: TButton; Edit1: TEdit; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; Label1: TLabel; Edit2: TEdit; Label2: TLabel; Edit3: TEdit; Label3: TLabel; Edit4: TEdit; Label4: TLabel; Edit5: TEdit; Label5: TLabel; Edit6: TEdit; Label6: TLabel; Edit7: TEdit; Label7: TLabel; Edit8: TEdit; Label8: TLabel; Label9: TLabel; Edit9: TEdit; LabeledEdit3: TLabeledEdit; Button2: TButton; Label10: TLabel; Edit10: TEdit; Label11: TLabel; Edit11: TEdit; procedure Button1Click(Sender: TObject); procedure Button2Click(Sender: TObject); private { Private 宣言 } function second_imperfect_elliptic_integral(Q, K: Extended; var EBnKnAns, FBnKnAns: Extended): boolean; function second_imperfect_elliptic_integral_bignum_arithmetic(strk, strQ: string; var EBnKnAns, FBnKnAns: mp_float): boolean; procedure bignum_arithmetic; public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses Math; //------------------------------- // 第１種第２種楕円積分 // FBnKn[0] 第１種楕円積分解 // EBnKn[0] 第２種楕円積分解 // ランデン変換 // Q 角度 deg // K 離心率 // 多倍長演算 MPArith を使用 //------------------------------- function TForm1.second_imperfect_elliptic_integral_bignum_arithmetic(strk, strQ: string; var EBnKnAns, FBnKnAns: mp_float): boolean; label OUTEX, OUTTR; const K180 = 180; K90 = 90; K2 = 2; K1 = 1; var I, MI : integer; Kn : array of mp_float; // Kn knd : array of mp_float; // k'n N2SKn : array of mp_float; // 2/(1+Kn) T2SKnd : array of mp_float; // П2/(1+Kn') BRad : array of mp_float; // β(rad) SinBn : array of mp_float; // sinβn FBnKn : array of mp_float; // F(βn,kn) EBnKn : array of mp_float; // E(βn,kn) LnD : mp_float; mp_pi : mp_float; tmp : mp_float; tmp0 : mp_float; mp_180 : mp_float; mp_90 : mp_float; mp_i : mp_float; Emp : mp_float; Qmp, Kmp : mp_float; tmp1,tmp2 : mp_float; mp_1, mp_2 : mp_float; // str : mp_string; astrK : ansistring; astrQ : ansistring; mperrF : boolean; K : extended; begin result := false; mperrF := false; mpf_init(LnD); mpf_init(mp_pi); mpf_init(tmp); mpf_init(tmp0); mpf_init(mp_180); mpf_init(mp_90); mpf_init(mp_i); mpf_init(Emp); mpf_init2(Qmp, Kmp); mpf_init2(tmp1,tmp2); mpf_init2(mp_1, mp_2); // Kのセット // K 一旦extendedに変換 K := strtofloat(strk); // 値が 1E-4951 で桁落ちしたらゼロになります double の場合1E-309 if K = 0 then strk := '0'; astrK := ansistring(strk); // K の値が非常にゼロに近い場合エラーになるので一応確認 // K < 1E-10000----- try mp_real.mpf_read_decimal(Kmp, PAnsiChar(astrK)); except // on MPXBAdarg do ShowMessage('MpfError Raised'); on MPXBAdarg do mperrF := true; end; if mperrF then begin ShowMessage('Mpf Error Raised'); goto OUTTR; end; // Kの値から配列の大きさせっていします mp_real.mpf_read_decimal(tmp, PAnsiChar(astrK)); MI := 0; // empとtmpで同じ値が出るまで繰り返します repeat inc(MI); mpf_add_int(tmp, 0, Emp); // Emp = tmp mpf_sqrt(tmp, tmp1); // tmp1 = sqrt(tmp) mpf_Mul_int(tmp1, 2, tmp2); // tmp2 = 2 * sqrt(tmp) mpf_add_int(tmp, 1, tmp0); // tmp0 = 1 + tmp mpf_div(tmp2, tmp0, tmp); // tmp = (2 * sqrt(tmp)) / (1 + tmp) until mpf_is_eq(Emp, tmp); // Emp と tmp が等しかったら終了 setlength(Kn, MI); // Kn setlength(knd, MI); // k'n setlength(N2SKn, MI); // 2/(1+Kn) setlength(T2SKnd, MI); // П2/(1+Kn') setlength(BRad, MI); // β(rad) setlength(SinBn, MI); // sinβn setlength(FBnKn, MI); // F(βn,kn) setlength(EBnKn, MI); // E(βn,kn) dec(MI); for I := 0 to MI do begin mpf_init(kn[I]); mpf_init(knd[I]); mpf_init(N2SKn[I]); mpf_init(T2SKnd[I]); mpf_init(BRad[I]); mpf_init(SinBn[I]); mpf_init(FBnKn[I]); mpf_init(EBnKn[I]); end; // Qのセット astrQ := ansistring(strq); mp_real.mpf_read_decimal(Qmp, PAnsiChar(astrQ)); // 定数のセット mpf_set_int(mp_90, K90); mpf_set_int(mp_180, K180); mpf_set_int(mp_1, K1); mpf_set_int(mp_2, K2); mpf_set_pi(mp_pi); // K = 0 の時は円なのでpiの角度値rad。 if mpf_is0(Kmp) then begin mpf_mul(mp_pi, Qmp, tmp); mpf_div(tmp, mp_180, EBnKnAns); mpf_div(tmp, mp_180, FBnKnAns); result := true; goto OUTEX; end; // K = 1 で Q=90 の時 // 分割計算では答えが出るのでエラーに // ならない様にします。 mpf_abs(Qmp, tmp); if mpf_is1(Kmp) then begin if mpf_is_eq(tmp, mp_90) then begin mpf_set1(EBnKnAns); if s_mpf_is_neg(Qmp) then s_mpf_chs(EBnKnAns); result := true; goto OUTEX; end; if mpf_is_gt(tmp, mp_90) then begin goto OUTEX; end; end; // kn[0] := k; mp_real.mpf_read_decimal(KN[0], PAnsiChar(astrK)); for I := 1 to MI do begin // kn[I] := 2 * sqrt(Kn[I - 1])/(1 + Kn[I - 1]); mpf_add(kn[I - 1], mp_1, tmp); mpf_sqrt(Kn[I - 1], tmp0); mpf_div(tmp0, tmp, tmp1); mpf_mul(tmp1, mp_2, kn[I]); end; mpf_set1(knd[0]); for I := 1 to MI do begin // knd[I] := (1 - kn[I - 1]) / (1 + Kn[I - 1]); mpf_sub(mp_1, kn[I - 1], tmp); mpf_add(mp_1, kn[I - 1], tmp0); mpf_div(tmp, tmp0, knd[I]); end; for I := 0 to MI do begin // N2SKn[I] := 2 / (1 + kn[I]); mpf_add(mp_1, kn[I], tmp0); mpf_div(mp_2, tmp0, N2SKn[I]); end; // T2SKnd[MI] := N2SKn[MI]; mpf_div(mp_2, tmp0, T2SKnd[MI]); // str := mpf_decimal(T2SKnd[MI], 50); for I := MI - 1 downto 0 do // T2SKnd[I] := T2SKnd[I + 1] * N2SKn[I]; mpf_mul(T2SKnd[I + 1], N2SKn[I], T2SKnd[I]); // BRad[0] := Q / 180 * pi; mpf_div(Qmp, mp_180, tmp); mpf_mul(tmp, mp_pi, BRad[0]); for I := 1 to MI do begin // BRad[I] := (arcsin(kn[I - 1] * sin(Brad[I - 1])) + Brad[I - 1]) / 2; mpf_sin(Brad[I - 1], tmp); mpf_mul(kn[I - 1], tmp, tmp0); mpf_arcsin(tmp0, tmp); mpf_add(tmp, Brad[I - 1], tmp1); mpf_div(tmp1, mp_2, BRad[I]); end; for I := 0 to MI do // SinBn[I] := sin(Brad[I]); mpf_sin(Brad[I], SinBn[I]); // LnD := LN((1 + sin(Brad[MI])) / cos(Brad[MI])); // tmp = sin(Brad[MI] mpf_sin(Brad[MI], tmp); // tmp0 := 1 + sin(Brad[MI]) mpf_add(tmp, mp_1, tmp0); // tmp := cos(Brad[MI) mpf_cos(Brad[MI], tmp); // tmp0 := (1 + sin(Brad[MI])) / cos(Brad[MI]); mpf_div(tmp0, tmp, tmp0); // tmp0 <= 0 の場合自然対数変換できないので計算打ち切り if s_mpf_is_le0(tmp0) then goto OUTEX; // LnD := Ln(tmp0); mpf_Ln(tmp0, LnD); for I := 0 to MI do begin // FBnKn[I] := T2SKnd[I] * LnD; mpf_mul(T2SKnd[I], LnD, FBnKn[I]); if I = 0 then mpf_mul(T2SKnd[I], LnD, FBnKnans); end; // EBnKn[MI] := sin(Brad[MI]); mpf_sin(Brad[MI], EBnKn[MI]); for I := MI - 1 downto 0 do begin // EBnKn[I] := (2 * EBnKn[I + 1] + 2 * knd[I + 1] * FBnKn[I + 1]) / (1 + knd[I + 1]) - kn[I] * SinBn[I]; mpf_mul(EBnKn[I + 1], mp_2, tmp); mpf_mul(knd[I + 1], mp_2, tmp0); mpf_mul(tmp0, FBnKn[I + 1], tmp1); mpf_add(tmp, tmp1, tmp2); mpf_add(knd[I + 1], mp_1, tmp); mpf_div(tmp2, tmp, tmp0); mpf_mul(kn[I], SinBn[I], tmp); mpf_sub(tmp0, tmp, EBnKn[I]); end; // EBnKnans := EBnKn[0]; mpf_copy(EBnKn[0], EBnKnans); // str := mpf_decimal(EBnKn[0], 50); // str := mpf_decimal(kn[MI], 50); // Edit4.Text := string(str); result := true; OUTEX: for I := 0 to MI do begin mpf_clear(kn[I]); mpf_clear(knd[I]); mpf_clear(N2SKn[I]); mpf_clear(T2SKnd[I]); mpf_clear(BRad[I]); mpf_clear(SinBn[I]); mpf_clear(FBnKn[I]); mpf_clear(EBnKn[I]); end; OUTTR: mpf_clear(LnD); mpf_clear(mp_pi); mpf_clear(tmp); mpf_clear(tmp0); mpf_clear(mp_180); mpf_clear(mp_90); mpf_clear(mp_i); mpf_clear(Emp); mpf_clear2(Qmp, Kmp); mpf_clear2(tmp1,tmp2); mpf_clear2(mp_1, mp_2); end; //------------------------------------------------------------------- // 多倍長ランデン変換 // 入力桁数制限の為一度角度入力値stringをextendedの浮動小数点に変換し // 更にextendedからstringに変換しています。 //------------------------------------------------------------------- procedure TForm1.bignum_arithmetic; label ERREXIT; var EBnKnans, EBnKn90 : mp_float; tmp, EBnKnAll : mp_float; FBnKnAll : mp_float; FBnKnans, FBnKn90 : mp_float; Q, AQ : Extended; strK, strQ : string; str : ansistring; I, J : integer; KnAllF : boolean; begin mpf_init2(EBnKnans, EBnKn90); mpf_init2(tmp, EBnKnALL); mpf_init3(FBnKnans, FBnKn90, FBnKnAll); strK := LabeledEdit1.Text; strQ := LabeledEdit2.Text; // 一旦extendedに変換 Q := strtofloat(strQ); // Q値が 1E-4951 で桁落ちしたらゼロに設定 double で1E-309 if Q = 0 then strQ := '0' else strQ := floatTostr(Q); // 一括計算計算--------------------------------------------------------------------------- KnAllF := second_imperfect_elliptic_integral_bignum_arithmetic(strk, strQ, EBnKnAll, FBnknAll); // 計算結果の表示 if KnAllF then begin str := mpf_decimal(EBnKnAll, 50); Edit4.Text := string(str); str := mpf_decimal(FBnKnAll, 50); Edit9.Text := string(str); end else begin Edit4.Text := '計算出来ません"角度"又は"K"を小さくして下さい。'; Edit9.Text := '計算出来ません"角度"又は"K"を小さくして下さい。'; // goto ERREXIT; end; // 90°分割計算 -------------------------------------------------------------------------- strQ := '90'; // 計算用角度符号無しに AQ := ABS(Q); // 90°の倍数部計算 I := trunc(AQ / 90); // 90°計算 mpf_set0(EBnKn90); mpf_set0(FBnKn90); if I > 0 then second_imperfect_elliptic_integral_bignum_arithmetic(strk, strQ, EBnKn90, FBnKn90); // 90°の倍数角に対する余り角度計算 象限によって計算方法変更 if I mod 2 = 0 then strQ := floatTostr(AQ - 90 * I) else strQ := floatTostr(90 * (I + 1) - AQ); // 設定された余り角分の計算 second_imperfect_elliptic_integral_bignum_arithmetic(strk, strQ, EBnKnans, FBnKnans); // 90°倍数角分と余り角分の加算 象限によって計算方法変更 if I mod 2 = 0 then begin J := I; mpf_mul_int(EBnKn90, J, tmp); mpf_add(tmp, EBnKnans, EBnKnans); mpf_mul_int(FBnKn90, J, tmp); mpf_add(tmp, FBnKnans, FBnKnans); end else begin J := I + 1; mpf_mul_int(EBnKn90, J, tmp); mpf_sub(tmp, EBnKnans, EBnKnans); mpf_mul_int(FBnKn90, J, tmp); mpf_sub(tmp, FBnKnans, FBnKnans); end; // 角度の符号に結果をあわせます。 if Q < 0 then begin s_mpf_chs(EBnKnans); s_mpf_chs(FBnKnans); end; // 計算結果の表示 str := mpf_decimal(EBnKnans, 50); Edit5.Text := string(str); // K = 1 では 90°以上の第一種積分は不可で∞になります。 if (strTofloat(strK) >= 1) and (AQ >= 90) then begin str := '∞'; Edit9.Text := string(str); end else str := mpf_decimal(FBnKnans, 50); Edit8.Text := string(str); // 差分の表示 if KnAllF then begin mpf_sub(EBnKnAll, EBnKnans, tmp); str := mpf_decimal(tmp, 50); Edit6.Text := string(str); end else Edit6.Text :=''; ERREXIT: mpf_clear3(FBnKnans, FBnKn90, FBnKnAll); mpf_clear2(EBnKnans, EBnKn90); mpf_clear2(tmp, EBnKnAll); end; //------------------------------- // 第１種第２種楕円積分 // FBnKn[0] 第１種楕円積分解 // EBnKn[0] 第２種楕円積分解 // ランデン変換 // Q 角度 deg // K 離心率 //------------------------------- function TForm1.second_imperfect_elliptic_integral(Q, K: Extended; var EBnKnAns, FBnKnAns: Extended): boolean; var I, MI : integer; Kn : array of Extended; // Kn knd : array of Extended; // k'n N2SKn : array of Extended; // 2/(1+Kn) T2SKnd : array of Extended; // П2/(1+Kn') BRad : array of Extended; // β(rad) SinBn : array of Extended; // sinβn FBnKn : array of Extended; // F(βn,kn) EBnKn : array of Extended; // E(βn,kn) LnD, nD : Extended; begin result := true; // 配列の設定 // 同じ値"1"が出るまでくりかえします。 // LND = 1 での判定は使用できません // デバッグ上の表示は"1" でも最終ビット付近に誤差があります MI := 0; LnD := K; repeat inc(MI); nD := LnD; LnD := 2 * sqrt(nD) / (1 + nD); until LND = nD; setlength(Kn, MI); // Kn setlength(knd, MI); // k'n setlength(N2SKn, MI); // 2/(1+Kn) setlength(T2SKnd, MI); // П2/(1+Kn') setlength(BRad, MI); // β(rad) setlength(SinBn, MI); // sinβn setlength(FBnKn, MI); // F(βn,kn) setlength(EBnKn, MI); // E(βn,kn) dec(MI); // K = 0 の時は円なのでpiの角度値rad。 if K = 0 then begin EBnKnAns := pi * Q / 180; FBnKnAns := EBnKnAns; exit; end; // K = 1 で Q=90 の時 // 分割計算では答えが出るのでエラーに // ならない様にします。 if K = 1 then begin if abs(Q) = 90 then begin if Q > 0 then EBnKnAns := 1 else EBnKnAns := -1; FBnKnAns := 0; // 実際は∞ // FBnKnAns := MAXExtended; exit; end; if abs(Q) > 90 then begin result := False; // 演算エラー設定 exit; end; end; // 1 > K > 0 の時 kn[0] := K; for I := 1 to MI do kn[I] := 2 * sqrt(Kn[I - 1])/(1 + Kn[I - 1]); knd[0] := 1; for I := 1 to MI do knd[I] := (1 - kn[I - 1]) / (1 + Kn[I - 1]); for I := 0 to MI do N2SKn[I] := 2 / (1 + kn[I]); T2SKnd[MI] := N2SKn[MI]; for I := MI - 1 downto 0 do T2SKnd[I] := T2SKnd[I + 1] * N2SKn[I]; BRad[0] := Q / 180 * pi; for I := 1 to MI do BRad[I] := (arcsin(kn[I - 1] * sin(Brad[I - 1])) + Brad[I - 1]) / 2; for I := 0 to MI do SinBn[I] := sin(Brad[I]); nD := (1 + sin(Brad[MI])) / cos(Brad[MI]); // nd が ０より大きくないと自然対数に変換できません。 if nD <= 0 then begin result := False; exit; end; LnD := LN(nD); for I := 0 to MI do FBnKn[I] := T2SKnd[I] * LnD; EBnKn[MI] := sin(Brad[MI]); for I := MI - 1 downto 0 do EBnKn[I] := (2 * EBnKn[I + 1] + 2 * knd[I + 1] * FBnKn[I + 1]) / (1 + knd[I + 1]) - kn[I] * SinBn[I]; EBnKnAns := EBnKn[0]; FBnKnAns := FBnKn[0]; end; //--------------------------------------------------------- // 角度微小角分割計算とランデン変換による計算 // 離心率Kの値が0.9を超えると、積分できる角度が制限されます。 // K = 1 の場合は 積分できるのは90°迄です。 // 角度微小角分割による計算は、K=1 でも問題なく計算できます。 //--------------------------------------------------------- procedure TForm1.Button1Click(Sender: TObject); var I, N : integer; K, Q, dq, Wq : Extended; x1, y1, x2, y2 : Extended; S, ds, b : Extended; dx, dy : Extended; rnd, Frnd : Extended; RAN90, Qd : Extended; RANQd, RANQ : Extended; D90, SDQ, AQ : Extended; FAN90, FANQ : Extended; FANQd : Extended; rndF : boolean; // 微小角分割積分 procedure elliptic_integera(Q : Extended); var I : integer; begin N := round(Q * 10000); // 分割数設定 N := abs(N); if N = 0 then N := 1; // 零での除算防止 Q := Q / 180 * pi; // 角度radに変換 dq := Q / N; // Δα計算 S := 0; // 積分値クリア x1 := cos(0) * b; // x1=cos()*bは短軸基準 長軸基準はx1=cos() y1 := sin(0); // y1=sin() は短軸基準 長軸基準はy1=sin()*b for I := 1 to N do begin // 指定角α迄積分計算 wq := I * dq; x2 := cos(wq) * b; // x2=cos()*bは短軸基準 長軸基準はx2=cos() y2 := sin(wq); // y2=sin() は短軸基準 長軸基準はy2=sin()*b dx := x2 - x1; dy := y2 - y1; ds := sqrt(dx * dx + dy * dy); // 微小角の距離 S := S + ds; // 総和 Σ x1 := x2; y1 := y2; end; end; begin val(LabeledEdit1.Text, K, I); if I <> 0 then begin application.MessageBox('Kの値に間違いがあります。','離心率K',0); exit; end; if K > 1 then begin application.MessageBox('Kの値は１迄です。','離心率K',0); exit; end; if K < 0 then begin application.MessageBox('Kの値がゼロ以下です。','離心率K',0); exit; end; val(LabeledEdit2.Text, Q, I); if I <> 0 then begin application.MessageBox('αの値に間違いがあります。','積分角α',0); exit; end; // 積分範囲Xに変換 D90 := int(Q / 90); // 90°の整倍数 SDQ := Q - D90 * 90; // 残りの角度 SDQ := SDQ / 180 * pi; // radに変換 AQ := sin(SDQ) + D90; // sin変換 Labelededit3.Text := floatTostr(AQ); // 積分範囲Xセット // 多倍長によるランデン変換計算------------------------------------------- bignum_arithmetic; // ランデン変換による計算------------------------------------------------- // 計算用角度を符号なしに AQ := abs(Q); rndF := second_imperfect_elliptic_integral(Q, K, rnd, Frnd); if rndF then begin Edit2.Text := floatTostr(rnd); // K = 1 では 90°以上の第一種積分は不可で∞になります。 if (K = 1) and (AQ >= 90) then Edit10.Text := '∞' else Edit10.Text := floatTostr(Frnd); end else begin Edit2.Text := '計算出来ません"角度"又は"K"を小さくして下さい。'; Edit10.Text := '計算出来ません"角度"又は"K"を小さくして下さい。'; end; // 90°分割ランデン変換--------------------------------------------------- // 90°の倍数部計算 I := Trunc(AQ / 90); // 90°分の計算 RAN90 := 0; FAN90 := 0; if I > 0 then second_imperfect_elliptic_integral(90, K, RAN90, FAN90); // 計算範囲の設定 象限によって残り部分の設定 if I mod 2 = 0 then Qd := AQ - I * 90 else Qd := (I + 1) * 90 - AQ; // 設定された残り範囲の計算 second_imperfect_elliptic_integral(Qd, K, RANQd, FANQd); // 入力角度の積分値計算 象限によって計算変更 if I mod 2 = 0 then begin RANQ := I * RAN90 + RANQd; FANQ := I * FAN90 + FANQd; end else begin RANQ := (I + 1) * RAN90 - RANQd; FANQ := (I + 1) * FAN90 - FANQd; end; // 角度符号によって符号設定 if Q < 0 then begin RANQ := -RANQ; FANQ := -FANQ; end; Edit7.Text := floatTostr(RANQ); // K = 1 では 90°以上の第一種積分は不可で∞になります。 if (K = 1) and (AQ >= 90) then begin Edit10.Text := '∞'; Edit11.Text := '∞'; end else Edit11.Text := floatTostr(FANQ); // 角度微小角分割による積分計算------------------------------------------- // 90°分割 分割しなくても微小角積分なので出来ますが計算速度を上げるため // 90°単位で区切って計算します。 // 大きな角度でも、最大で180°分の計算で済みます。 // 半径b計算 半径aは１で省略 b := sqrt(1 - K * K); // 90°の倍数部計算 I := Trunc(AQ / 90); // 90°分の積分値計算 S := 0; if I > 0 then elliptic_integera(90); D90 := S; // 90度の積分値 // 計算範囲の設定 象限によって残り部分の設定 if I mod 2 = 0 then Qd := AQ - I * 90 else Qd := (I + 1) * 90 - AQ; // 設定された残り範囲の計算 elliptic_integera(Qd); // 入力角度の積分値計算 象限によって計算変更 if I mod 2 = 0 then SDQ := I * D90 + S else SDQ := (I + 1) * D90 - S; // 距離の計算なので符号なし、角度符号に合わせて符号設定します。 if Q < 0 then SDQ := -SDQ; Edit1.Text := floattostr(SDQ); // 差分計算表示----------------------------------------------------------- if rndF then // rndF = false 演算エラー Edit3.Text := floattostr(rnd - SDQ) else Edit3.Text := ''; end; procedure TForm1.Button2Click(Sender: TObject); var Q, X : double; XS, J : double; Qs : double; ch : integer; begin val(Labelededit3.Text, X, Ch); if ch <> 0 then begin application.MessageBox('Xの値に間違いがあります。','積分範囲X',0); exit; end; J := int(X); // 整数部 Xs := X - J; // 小数部取り出し Qs := arcsin(Xs) / pi * 180; // 小数部角度degに変換 Q := J * 90 + Qs; // 整数部角度と小数部角度加算 Labelededit2.Text := floatTostr(Q); // 積分角度αにセット Button1Click(nil); // 積分実行 end; end.
second_imperfect_elliptic_integra_division_bignum_arithmetic.zip