平方根　立方根の解法

　逆三角関数の計算で、Delphiの組み込み関数をを出来る限り使わずに計算するようにプログラムを組みましたが、その中にルートの計算が、Delphiの組み込み関数として残っていたので、ルートの解法のプログラムを作成してみました。

　ルートの解法をする方法として、代表的なものに、二分法と、ニュートン法あります。
　二分法は、目的の解放値に対して、大きい値と、小さい値を仮に与えて、その差の二分の一の値を小さいほうの値に加算して、計算し、計算した結果が大きい場合、大きいほうの値を計算に使用した値に変更し、計算した結果が小さい場合は、小さいほうの値を、計算に使用した値に変更し、再度計算を繰り消えすことで、大きいほうの値と、小さいほうの値の差の二分の一づつ正解に近づけます。
　ニュートン法は、f(x)と、微分したf'(x)の値から、近似値の計算を行いますが。

上記以外にも近似値を求める方法はありますが、ニュートン法が一番早く近似値を求めることができます。

平方根、立方根の解法アルゴリズムの説明については、"平方根　アルゴリズム" で Google 検索を行えば、沢山検索されるので、そちらを参照してください。

平方根の解法は、紀元前１７世紀の古代バビロンの時代から知られているようです。
WikipediaのMethods of computing square roots　を参照してください。

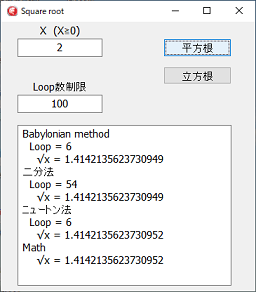　Doubleの有効桁数15～16桁迄は一致しているので問題ない答えとなっています。
バビロンの平方根の計算はニュートン法と、大差ない速度で収束します。
立方根については、平方根と同じ考えで計算式をつくりましたが、二分法よりは、少しマシなループ数となります。
Mathでの計算は、Delphiに組み込まれた関数で計算された値です。
　ループ数制限値は、通常の計算では、この値に達しませんが、一回の計算の値、二回の計算の値のループの制限をして、収束していく過程を見る為のものです。
プログラムを少し修正すれば、収束の過程を表示するように出来ます。

プログラム

　収束判定で一つ前の値と同じになったら収束と判定すると、収束判定が出来ずに、ループから抜け出すことが出来なくなることがあります。
その対策として、一定のループ数に達したら、ループから抜け出すようにする方法もあるのですが、その場合計算に無駄な時間がかかります。
収束判定が出来なくなる理由は、収束時、同じ二つの値を交互に繰り返してしまう為です、そこで、一つ前だけではなく、二つ前の値も、収束判定に利用すれば、確実に収束判定が出来ます。
三つの値をループするような事は、無いと思われます。
epsilon(エプシロン　１に対して、加算できる最小値)を利用して、収束判定をするのが一般的ですが、少しでも、誤差を小さくするため、同じ値が繰り返す事を収束の判定に利用しています。

unit Main;

interface

uses
  Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
  Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls;

type
  TForm1 = class(TForm)
    LabeledEdit1: TLabeledEdit;
    BitBtn1: TBitBtn;
    Memo1: TMemo;
    BitBtn2: TBitBtn;
    LabeledEdit2: TLabeledEdit;
    procedure BitBtn1Click(Sender: TObject);
    procedure BitBtn2Click(Sender: TObject);
  private
    { Private 宣言 }
  public
    { Public 宣言 }
  end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

uses system.Math;

// 平方根 Babylonian method
function sqrt_Babylonian(k: double; j: integer): double;
label
  EXT;
var
  x, bx : double;
  i: integer;
begin
  i := 0;
  if (k = 0) or (k = 1) then begin
    result := k;
    goto EXT;
  end;
  x := k;
  if k < 1 then X := 1;
  i := 0;
  repeat
    bx := x;
    x := (x + (k / x)) /2;
    inc(i);
  until (bx = x) or (i >= j);
  result := x;
EXT:
  Form1.Memo1.Lines.Append('  Loop = ' + intTostr(i));
end;

// 平方根 二分法
function sqrt_by_bisection(k: double; j: integer): double;
label
  EXT;
var
  def           : double;
  upper, bottom : double;
  m             : double;
  i             : integer;
begin
  i := 0;
  if (k = 0) or (k = 1) then begin
    result := k;
    goto EXT;
  end;
  upper := k;
  if k < 1 then upper := 1;
  bottom := 0;
  i := 0;
  repeat
    def := abs(upper - bottom);
    m := (bottom + upper) / 2;
//    m := bottom + (upper - bottom) / 2;
    if m * m > k then upper := m
                 else bottom := m;
    inc(i);
  until (abs(upper - bottom) = def) or (i >= j);
  result := bottom;
EXT:
  Form1.Memo1.Lines.Append('  Loop = ' + intTostr(i));
end;

// 平方根 ニュートン法
// X=√k
// X^2 = k
// X^2-k = 0   f(X) = X^2 - K
// 微分　　　　f'(X) = 2X
// Xn+1 = Xn-f(X)/f'(X)
// Xn+1 = Xn-(X^2-k)/(2X)
function sqrt_by_newton(k: double; j: integer): double;
label
  EXT;
var
  bx, x, next_x: double;
  i : integer;

  function f(d: double): double;
  begin
    result := d - (d * d - k) / (2 * d);
  end;

begin
  i := 0;
  if (k = 0) or (k = 1) then begin
    result := k;
    goto EXT;
  end;
  x := k;
  next_x := f(x);
  repeat
    bx := x;
    x := next_x;
    next_x := f(x);
    inc(i);
  until (x = next_x) or (bx = next_x) or (i >= j);
  result := next_x;
EXT:
  Form1.Memo1.Lines.Append('  Loop = ' + intTostr(i));
end;

// 立法根 Babylonian method
function cubic_Babylonian(k: double; j: integer): double;
label
  EXT;
var
  ax, bx, x : double;
  i         : integer;
begin
  i := 0;
  if (k = 0) or (k = 1) then begin
    result := k;
    goto EXT;
  end;
  x := k;
  if k < 1 then x := 1;
  i := 0;
  bx := k;
  repeat
    ax := bx;
    bx := x;
    x := (x + (k / x / x)) / 2;
    inc(i);
  until (ax = x) or (bx = x) or (i >= j);
  result := x;
EXT:
  Form1.Memo1.Lines.Append('  Loop = ' + intTostr(i));
end;

// 立法根 二分法
function cubic_root_bisection(k: double; j: integer): double;
label
  EXT;
var
  def           : double;
  upper, bottom : double;
  m             : double;
  i             : integer;
begin
  i := 0;
  if (k = 0) or (k = 1) then begin
    result := k;
    goto EXT;
  end;
  upper := k;
  if k < 1 then upper := 1;
  bottom := 0;
  i := 0;
  repeat
    def := abs(upper - bottom);
    m := (bottom + upper) / 2;
//    m := bottom + (upper - bottom) / 2;
    if m * m * m > k then upper := m
                     else bottom := m;
    inc(i);
  until (abs(upper - bottom) = def) or (i >= j);
  result := bottom;
EXT:
  Form1.Memo1.Lines.Append('  Loop = ' + intTostr(i));
end;

// 立方根　ニュートン法
// X = K^1/3
// X^3 = K
// X^3 - K = 0    f(X) = X^3 - K
//  微分          f'(X) = 3X^2
// Xn+1 = Xn-(X^3-k)/(3X^2)
function cubic_root_newton(k: double; j:integer): double;
label
  EXT;
var
  bx, x, next_x: double;
  i : integer;

  function f(d: double): double;
  begin
    result := d - (d * d * d - k) / (3 * d * d);
  end;

begin
  i := 0;
  if (k = 0) or (k = 1) then begin
    result := k;
    goto EXT;
  end;
  x := k;
  next_x := f(x);
  repeat
    bx := x;
    x := next_x;
    next_x := f(x);
    inc(i);
  until (x = next_x) or (bx = next_x) or (i >= j);
  result := next_x;
EXT:
  Form1.Memo1.Lines.Append('  Loop = ' + intTostr(i));
end;

// 平方根計算
procedure TForm1.BitBtn1Click(Sender: TObject);
var
  x, ax , sq  : double;
  ch, j       : integer;
begin
  val(labelededit1.Text, x, ch);
  if ch <> 0 then begin
    application.MessageBox('入力値に誤りがあります。','注意',0);
    exit;
  end;
  val(labelededit2.Text, j, ch);
  if ch <> 0 then begin
    application.MessageBox('入力値に誤りがあります。','注意',0);
    exit;
  end;
  memo1.Clear;
  ax := abs(x);
  Memo1.Lines.Append('Babylonian method');
  sq := sqrt_Babylonian(ax, j);
  if x < 0 then
    Memo1.Lines.Append('　　√x = ' + floatTostrF(sq, ffgeneral, 20, 5) + '　ｉ')
  else
    Memo1.Lines.Append('　　√x = ' + floatTostrF(sq, ffgeneral, 20, 5));
  Memo1.Lines.Append('二分法');
  sq := sqrt_by_bisection(ax, j);
  if x < 0 then
    Memo1.Lines.Append('　　√x = ' + floatTostrF(sq, ffgeneral, 20, 5) + '　ｉ')
  else
    Memo1.Lines.Append('　　√x = ' + floatTostrF(sq, ffgeneral, 20, 5));
  Memo1.Lines.Append('ニュートン法');
  sq := sqrt_by_newton(ax, j);
  if x < 0 then
    Memo1.Lines.Append('　　√x = ' + floatTostrF(sq, ffgeneral, 20, 5) + '　ｉ')
  else
    Memo1.Lines.Append('　　√x = ' + floatTostrF(sq, ffgeneral, 20, 5));
  Memo1.Lines.Append('Math');
  sq := sqrt(ax);
  if x < 0 then
    Memo1.Lines.Append('　　√x = ' + floatTostrF(sq, ffgeneral, 20, 5) + '　ｉ')
  else
    Memo1.Lines.Append('　　√x = ' + floatTostrF(sq, ffgeneral, 20, 5));
end;

// 立方根計算
procedure TForm1.BitBtn2Click(Sender: TObject);
var
  x, ax, cub  : double;
  ch, j       : integer;
begin
  val(labelededit1.Text, x, ch);
  if ch <> 0 then begin
    application.MessageBox('入力値に誤りがあります。','注意',0);
    exit;
  end;
  val(labelededit2.Text, j, ch);
  if ch <> 0 then begin
    application.MessageBox('入力値に誤りがあります。','注意',0);
    exit;
  end;
  ax := abs(x);
  memo1.Clear;
  Memo1.Lines.Append('Babylonian method');
  cub := cubic_Babylonian(ax, j);
  if x < 0 then cub := -cub;
  Memo1.Lines.Append('　　x^1/3 = ' + floatTostrF(cub, ffgeneral, 20, 5));
  Memo1.Lines.Append('二分法');
  cub := cubic_root_bisection(ax, j);
  if x < 0 then cub := -cub;
  Memo1.Lines.Append('　　x^1/3 = ' + floatTostrF(cub, ffgeneral, 20, 5));
  Memo1.Lines.Append('ニュートン法');
  cub := cubic_root_newton(ax, j);
  if x < 0 then cub := -cub;
  Memo1.Lines.Append('　　x^1/3 = ' + floatTostrF(cub, ffgeneral, 20, 5));
  Memo1.Lines.Append('Math');
  cub := power(ax, 1 /3);
  if x < 0 then cub := -cub;
  Memo1.Lines.Append('　　x^1/3 = ' + floatTostrF(cub, ffgeneral, 20, 5));
end;

end.

　Square_root.zip

　　三角関数、逆三角関数、その他関数　に戻る