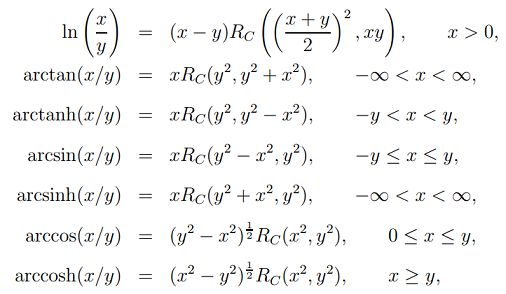
条件 y > 0
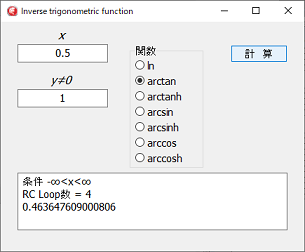
(注意) arctanh, arcsinh, arccosh は誤表記です、artanh, arsinh, arcosh が正規表現です。
Numerical computation of real or complex elliptic integralsの内容が、arc***hとなっていたのでそのまま使用しました。
逆三角関数の計算
Numerical computation of real or complex elliptic integralsの中に、カールソンの楕円積分RCを使用した逆三角関数、逆双曲線関数の計算があったのでプログラムを作成してみました。
実用には使用されないのですが、計算が出来るという参考プログラムです。
現在、関数計算は、CPUに浮動小数点演算として備わっているので、プログラムの中で、逆三角関数、逆双曲線関数のルーチンを組み込むことは、稀なことになっているようです。
CPUでの演算精度は、32ビットアプリケーションの場合、古いプログラムとの互換性から80ビットの演算、64ビットアプリケーションの場合、64ビットの演算となっています。
64ビットの場合、Doubleの精度なので、高い精度が必要な場合、多倍長演算が別途必要となります、この場合は関数は全てプログラムにより演算されることになり、マクローリン展開あたりを使用して計算されます。
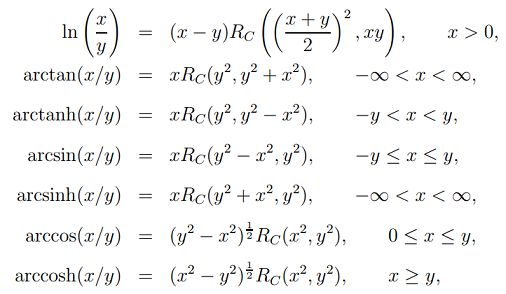
条件 y > 0

(注意) arctanh, arcsinh, arccosh は誤表記です、artanh, arsinh, arcosh
が正規表現です。
Numerical computation of real or complex elliptic integralsの内容が、arc***hとなっていたのでそのまま使用しました。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
Memo1: TMemo;
RadioGroup1: TRadioGroup;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses system.Math;
// カールソンの楕円積分 RC
//
// ---------------- RC ---------------------------------------------------------
function RC(x, y: double): double;
label
Ext;
const
// r = 1E-24;
Qc = 872; // power(3 * r, -1 / 8) = 871.68554
c1 = 3 / 10;
c2 = 1 / 7;
c3 = 3 / 8;
c4 = 9 / 22;
c5 = 159 / 208;
c6 = 9 / 8;
var
xt, yt, w, yb : double;
lamda, A0, Q : double;
s, Am, Qm : double;
m : integer;
begin
if y = 0 then begin
m := 0;
result := 0;
goto Ext;
end;
if y > 0 then begin
xt := x;
yt := y;
w := 1;
end
else begin
xt := x - y;
yt := - y;
w := sqrt(x / xt);
end;
yb := yt;
A0 := (xt + yt + yt) / 3;
Am := A0;
Q := Qc * abs(A0 - xt);
// Q := power(3 * r, -1 / 8) * abs(A0 - xt);
m := 0;
Qm := 1;
repeat
lamda := 2 * sqrt(xt) * sqrt(yt) + yt;
xt := (xt + lamda) / 4;
yt := (yt + lamda) / 4;
Am := (Am + lamda) / 4;
m := m + 1;
Qm := Qm / 4;
until (Qm * Q < abs(Am)) or (m > 100);
s := (yb - A0) * Qm / Am;
// s := (yb - A0) / power(4, m) / Am;
result := w * (1 + s * s * (c1 + s * (c2 + s * (c3 + s * (c4 + s * (c5 + s * c6)))))) / sqrt(Am);
Ext:
Form1.Memo1.Lines.Append('RC Loop数 = ' + intTostr(m));
end;
procedure TForm1.Button1Click(Sender: TObject);
var
x, y : double;
ans : double;
ch : integer;
CF : boolean;
begin
val(Labelededit1.Text, x, ch);
if ch <> 0 then begin
application.MessageBox('xの値に間違いがあります。','注意',0);
exit;
end;
val(Labelededit2.Text, y, ch);
if ch <> 0 then begin
application.MessageBox('yの値に間違いがあります。','注意',0);
exit;
end;
if y = 0 then begin
application.MessageBox('yの値は0(ゼロ)ではいけません。','注意',0);
exit;
end;
ans := 0;
memo1.Clear;
CF := True;
case radioGroup1.ItemIndex of
0: begin
memo1.Lines.Append('条件 x>0 & y>0');
if (x <= 0) or (y <= 0) then CF := False;
end;
1: memo1.Lines.Append('条件 -∞<x<∞');
2: begin
memo1.Lines.Append('条件 abs(x)<abs(y)');
if abs(x) >= abs(y) then CF := False;
end;
3: begin
memo1.Lines.Append('条件 abs(x)≦abs(y)');
if abs(x) > abs(y) then CF := False;
end;
4: memo1.Lines.Append('条件 -∞<x<∞');
5: begin
memo1.Lines.Append('条件 abs(x)≦abs(y)');
if abs(x) > abs(y) then CF := False;
end;
6: begin
memo1.Lines.Append('条件 abs(x)≧abs(y)');
if abs(x) < abs(y) then CF := False;
end;
end;
if not CF then begin
memo1.Lines.Append('因数が範囲外です。');
exit;
end;
if y < 0 then begin
y := -y;
x := -x;
end;
case radioGroup1.ItemIndex of
0: ans := (x - y) * RC((x + y) * (x + y) / 4, x * y);
1: ans := x * RC(y * y, y * y + x * x);
2: ans := x * RC(y * y, y * y - x * x);
3: ans := x * RC(y * y - x * x, y * y);
4: ans := x * RC(y * y + x * x, y * y);
5: ans := sqrt(y * y - x * x) * RC(x * x, y * y);
6: ans := sqrt(x * x - y * y) * RC(x * x, y * y);
end;
memo1.Lines.Append(floatTostr(ans));
end;
end.
![]() Inverse_trigonometric_function.zip
Inverse_trigonometric_function.zip
三角関数、逆三角関数、その他関数 に戻る