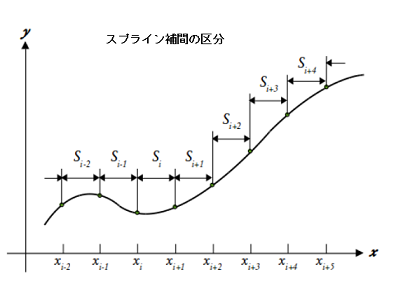
此処では、左図区分毎の三次計算式をたて、指定点を滑らかな曲線でつながるように連立方程式を解いて計算します。スプライン補間
ニュートン補間、ラグランジュ補間は、ルンゲ現象が発生するので、補間計算に使用するのには注意を要するのですが、区間毎に区切って三次多項式の補間を行うことで、ルンゲ現象を抑える事が出来ます。
二次平面上での、スプライン曲線は、通過点指定重曲線を参照してください。
此処では、左図区分毎の三次計算式をたて、指定点を滑らかな曲線でつながるように連立方程式を解いて計算します。
各区分でのｘでの ｙ＝Si(x) の値は次の様になります。
Ｓi(x)の値は次の連立一時方程式により ｓｉ を求める事に計算が出来ます。
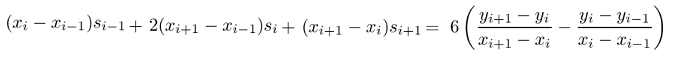
ｓｉ の値を求めたら次の計算により、区間任意の Ｘ に対する ｙ = S(x)の値を求める事が出来ます。
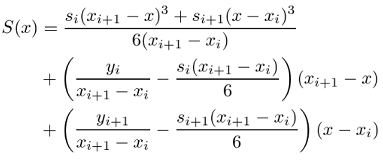
計算式の詳細は、Webでスプライン補間で検索してください。
次のプログラムは、上記計算式をそのままプログラムしたものです。
// Spline (スプライン) 補間 // xx xの値 // x[] xデーター配列 // y[] yデーター配列 // z[] 係数配列 function spline(xx: Double): Double; var d1, d2, d3 :Double; i, k :integer; begin // 補間関数値がどの区間にあるか検索 k := -1; for i := 1 to High(x) do begin if xx <= x[i] then begin k := i - 1; break; end; end; if k < 0 then // d > x(High(x)) k := High(x) - 1; // 補間値計算 d1 := x[k+1] - xx; d2 := xx - x[k]; d3 := x[k+1] - x[k]; result := (z[k] * power(d1,3) + z[k+1] * power(d2,3)) / d3 + (y[k] / d3 - z[k] * d3) * d1 + (y[k+1] / d3 - z[k+1] * d3) * d2; end; // Zテーブル作成 // ３項方程式を解く // x[] xデーター配列 // y[] yデーター配列 // z[] 係数配列 procedure trinomial_equation; var a, b, c, d, g, s : Darray; i, P : integer; begin // a,b,c,d,g,s配列の両端の値は0なのでN数より二個少なく宣言 P := High(x) - 1; setlength(a, P); setlength(b, P); setlength(c, P); setlength(d, P); setlength(g, P); setlength(s, P); // ３項方程式の係数の表を作る for i := 0 to P - 1 do begin a[i] := x[i + 1] - x[i]; b[i] := 2.0 * (x[i+2] - x[i]); c[i] := x[i+2] - x[i + 1]; d[i] := 6.0 * ((y[i+2] - y[i+1]) / (x[i+2] - x[i+1]) - (y[i+1] - y[i]) / (x[i+1] - x[i])); end; // ３項方程式を解く (ト－マス法) g[0] := b[0]; s[0] := d[0]; for i := 1 to P - 1 do begin g[i] := b[i] - a[i] * c[i-1] / g[i-1]; s[i] := d[i] - a[i] * s[i-1] / g[i-1]; end; // z[]の両端は0 c,g,sの配列はzより2個少ない z[0] := 0; z[P + 1] := 0; for i := P downto 1 do z[i] := (s[i-1] - c[i-1] * z[i+1]) / g[i-1]; for i := 1 to P do z[i] := z[i] / 6; end;
スプライン補間は、ニュートン補間に比べて、異常な値になる事は少ないのですが、それでも三次曲線であるため大きな振動が発生します。
その振動を抑えた秋間補間があるので、実際にプログラムして計算してみます。
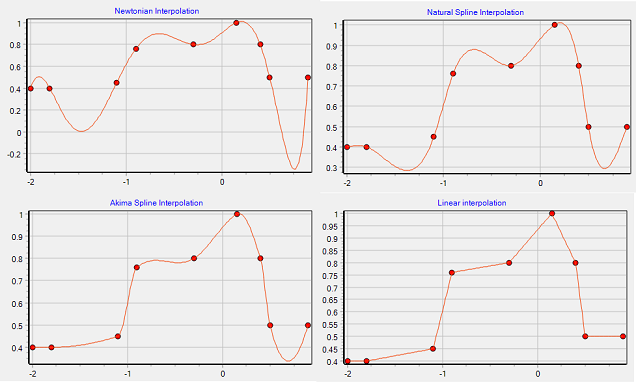
秋間スプラインは、区分の直線傾斜により補正されています。
しかし、実際の測定値のたいする補間を行うには、注意が必要ですが、ニュートン補間、スプライン補間に比べて、異常な値がでないようになっていると思います。
現実的には、非測定部の値を推定するにに三次曲線、多項式曲線を使用するのには無理があります。
問題を起こさないためには、直線補間を、多少滑らかな曲線を使用する場合は秋間補間の使用が良いように思われます。
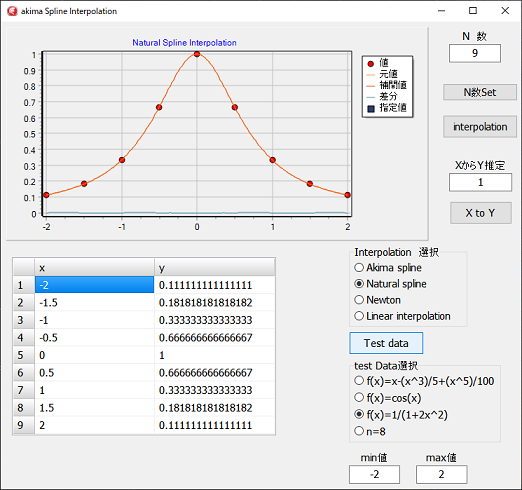左図は、今回のプログラムの実行画面ですが、スプライン補間は、計算上の理論的な値の補間に関しては、誤差が少なく良く補間されます。
しかし、何らかの実測値に対して、測定点以外の値の推定に、スプライン補間を使用するのは問題です。
データーの並び方によって、三次多項式特有の振幅がが発生するからです。
プログラム
プログラムリスト内 natural spline
は、前期splineのプログラムと計算手順は違いますが、計算結果は同じです。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, Vcl.StdCtrls,
VCLTee.TeEngine, VCLTee.Series, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart,
Vcl.Grids;
type
TForm1 = class(TForm)
Chart1: TChart;
StringGrid1: TStringGrid;
NEdit: TLabeledEdit;
NsetBtn: TButton;
interpolationBtn: TButton;
testdataBtn: TButton;
XEdit: TLabeledEdit;
Series1: TPointSeries;
Series2: TLineSeries;
Series3: TLineSeries;
Series4: TLineSeries;
Series5: TPointSeries;
Xin_interpolation: TButton;
RadioGroup1: TRadioGroup;
minxEdit: TLabeledEdit;
maxXEdit: TLabeledEdit;
RadioGroup2: TRadioGroup;
procedure testdataBtnClick(Sender: TObject);
procedure NsetBtnClick(Sender: TObject);
procedure interpolationBtnClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Xin_interpolationClick(Sender: TObject);
private
{ Private 宣言 }
procedure GridSet(Sin, Colin: integer);
procedure FGridSet(Sin, Colin: integer); // グリッドサイズ変更
procedure ndisp;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses system.Math;
type
DArray = array of double;
var
x, y : Darray; // x,y データー
m, t : Darray; // akoma 補間用テーブル
z : Darray; // Cubic 補間テーブルデーター
nt : Darray; // newtonian 補間テーブル
lz : Darray; // Linear 補間傾斜テーブル
DEF : Boolean; // 差分表示フラグ
xmax, xmin : double; // xデーターの最大値,最小値
dx : double; // グラフ作成用Δx
// グリッドサイズの変更
procedure TForm1.GridSet(Sin, Colin: integer); // グリッドサイズ変更
var // データー行の数は10迄
H, W :integer; // それ以上はスクロールする
begin
if (StringGrid1.ColCount = Colin) and (StringGrid1.RowCount = Sin) then exit;
StringGrid1.ColWidths[0] := 30;
StringGrid1.ColCount := Colin;
StringGrid1.RowCount := Sin;
if Sin <= 11 then // ストリンググリッドの大きさ設定
begin // 固定行を含め11行又はそれ以下の場合
H := (StringGrid1.DefaultRowHeight + 1) * Sin;
W := (StringGrid1.DefaultColWidth + 1) * (Colin - 1) + 31;
StringGrid1.ScrollBars := ssNone; // スクロールバーなし
end
else
begin // 固定行を含め11行より多い場合
H := (StringGrid1.DefaultRowHeight + 1) * (10 + 1);
W := (StringGrid1.DefaultColWidth + 1) * (Colin - 1) + 31;
StringGrid1.ScrollBars := ssVertical; // スクロールバー表示
end;
StringGrid1.ClientWidth := W;
StringGrid1.ClientHeight := H;
end;
// グリッド固定行の設定
procedure TForm1.FGridSet(Sin, Colin: integer);
var
E : integer;
begin
GridSet(Sin, Colin);
for E := 1 to Sin - 1 do
StringGrid1.Rows[E].Text := intTostr(E);
StringGrid1.Cols[1].Text := 'x';
StringGrid1.Cols[2].Text := 'y';
end;
// xの値チェック 同じxの値があるか確認 同じ値無 true 有り false
function datacheck(x :DArray; N: integer): boolean;
var
i, j : integer;
begin
result := false;
for i := 0 to N - 1 do
for j := 0 to N - 1 do begin
if i <> j then
if x[i] - x[j] = 0 then begin
application.MessageBox(pchar('x' + inttostr(i+1) + '-x' + inttostr(j+1)
+ 'がゼロになります。'),'注意',0);
exit;
end;
end;
for i := 0 to N - 2 do
if x[i] > x[i + 1] then begin
application.MessageBox(pchar('x' + inttostr(i+1) + '>x' + inttostr(i+2)
+ #13#10 +'値の大きさが逆です。'),'注意',0);
exit;
end;
result := true;
end;
// エラー result < 0
function Ninput: integer;
var
N, ch : integer;
begin
result := -1;
val(Form1.Nedit.Text, N, ch);
if ch <> 0 then begin
application.MessageBox('N数の入力に間違いが有ります。','注意',0);
exit;
end;
if N > 100 then begin
application.MessageBox('N数は100迄にして下さい。','注意',0);
exit;
end;
if N < 3 then begin
application.MessageBox('N数は3以上にして下さい。','注意',0);
exit;
end;
Form1.GridSet(N + 1, 3);
result := N;
end;
// グリッドN数セット
procedure TForm1.NsetBtnClick(Sender: TObject);
begin
ninput;
end;
// 参考値f(x) ルンゲ現象確認用データー
function f2(x: double): double;
begin
result := 1 / (1 + 2 * x * x);
end;
// 参考値 cos(x)
function f1(x: double): double;
begin
result := cos(x);
end;
// 参考値の関数
function f(x:Double):Double;
begin
result := x - power(x,3) / 5 + power(x,5) / 100;
end;
// 参考値 セット
procedure TForm1.testdataBtnClick(Sender: TObject);
var
N, ch : integer;
i : integer;
d, dx : double;
minx, maxx : double;
begin
if radiogroup1.ItemIndex < 3 then begin
N := Ninput;
if N < 0 then exit;
val(minxedit.Text, minx, ch);
if ch <> 0 then begin
application.MessageBox('min値に間違いが有ります。','注意',0);
exit;
end;
val(maxxedit.Text, maxx, ch);
if ch <> 0 then begin
application.MessageBox('max値に間違いが有ります。','注意',0);
exit;
end;
if minx >= maxx then begin
application.MessageBox('max値がmin値より小さいです。','注意',0);
exit;
end;
if radiogroup1.ItemIndex < 3 then begin
setlength(x, N);
setlength(y, N);
dx := (maxx - minx) / (N - 1);
for i := Low(x) to High(x) do begin
d := i * dx + minx;
x[i] := d;
case radiogroup1.ItemIndex of
0 : y[i] := f(d);
1 : y[i] := f1(d);
2 : y[i] := f2(d);
end;
StringGrid1.cells[1,i + 1] := floatTostr(x[i]);
StringGrid1.cells[2,i + 1] := floatTostr(y[i]);
end;
end;
DEF := True; // 差分グラフ表示フラグ
end;
if radiogroup1.ItemIndex = 3 then begin
N := 9; // データー数
Nedit.Text := inttostr(N);
GridSet(N + 1, 3);
setlength(x, N);
setlength(y, N);
x[0] := -2 ; y[0] := 0.4;
x[1] := -1.8; y[1] := 0.4;
x[2] := -1.1; y[2] := 0.45;
x[3] := -0.9; y[3] := 0.76;
x[4] := -0.3; y[4] := 0.8;
x[5] := 0.15; y[5] := 1;
x[6] := 0.4; y[6] := 0.8;
x[7] := 0.5; y[7] := 0.5;
x[8] := 0.9; y[8] := 0.5;
for i := 0 to N - 1 do begin
StringGrid1.cells[1,i + 1] := floatTostr(x[i]);
StringGrid1.cells[2,i + 1] := floatTostr(y[i])
end;
DEF := false; // 差分グラフ表示フラグ
end;
interpolationBtnClick(Nil);
end;
// Linear傾斜テーブル作成
procedure Linear_maketable;
var
i, p : integer;
begin
p := high(x);
for i := 0 to p - 1 do lz[i] := (y[i + 1] - y[i]) / (x[i + 1] - x[i]);
end;
// Linear補間
// x[] xデーター配列
// y[] yデーター配列
// lz[] 傾斜配列
function Linear_interpolation(xx: double): double;
var
iB, iM, iT: integer;
a : double;
begin
iB := low(x); // x[] bottom 配列no
iT := high(x); // x[] top配列No
// xx値の上下の配列xの配列番号を探す
// XX<x[iB]の場合一番下の区間 XX>x[iT]の場合一番上の区間
while (iT - iB) > 1 do begin
iM := (iB + iT) div 2; // middle配列no
if x[iM] > xx then
iT := iM
else
iB := iM;
end;
a := xx - x[iB]; // x[iB]からのxの値
result := y[iB] + lz[iB] * a;
end;
// ニュートン係数テーブル設定
// x[] xデーター配列
// y[] yデーター配列
// nt[] 係数配列
procedure Newtonian_maketabler; // 係数を求めntに上書き
var
i, j, P : integer;
begin
p := high(x);
for i := 1 to P do
for j := P downto i do
nt[j] := (nt[j] - nt[j - 1]) / (x[j] - x[j - i]);
end;
// ニュートン補間計算
// x[] xデーター配列
// nt[] 係数配列
function interpolate(xx: double): double; // 補間
var
i, P : integer;
r, s : double;
begin
p := high(x);
r := nt[0];
s := 1;
for i := 1 to P do begin
s := s * (xx - x[i - 1]);
r := r + s * nt[i];
end;
result := r
end;
// natural テーブルz作成
// x[] xデーター配列
// y[] yデーター配列
// z[] 係数配列
procedure maketable;
var
i, N : integer;
t : double;
h, d: DArray;
begin
N := high(x) + 1;
setlength(h, N);
setlength(d, N);
for i := 0 to N - 2 do begin
h[i ] := x[i + 1] - x[i];
d[i + 1] := (y[i + 1] - y[i]) / h[i];
end;
z[0] := 0;
z[N - 1] := 0; // y''(x)両端の値 0
z[1] := d[2] - d[1];
d[1] := 2 * (x[2] - x[0]);
for i := 1 to N - 3 do begin
t := h[i] / d[i];
z[i + 1] := d[i + 2] - d[i + 1] - z[i] * t;
d[i + 1] := 2 * (x[i + 2] - x[i]) - h[i] * t;
end;
z[N - 2] := z[N - 2] - h[N - 2] * z[N - 1];
for i := N - 2 downto 1 do
z[i] := (z[i] - h[i] * z[i + 1]) / d[i];
end;
// natural Spline 補間
// t xxの値
// x[] xデーター配列
// y[] yデーター配列
// z[] 係数配列
function spline(t: double): double;
var
i, j, k: integer;
d, h: double;
begin
j := high(x);
i := 0;
// 補間関数値がどの区間にあるか検索
while i < j do begin
k := (i + j) div 2;
if x[k] < t then i := k + 1
else j := k;
end;
if i > 0 then dec(i);
// 補間値計算
h := x[i + 1] - x[i];
d := t - x[i];
result := (((z[i + 1] - z[i]) * d / h + z[i] * 3) * d
+ ((y[i + 1] - y[i]) / h
- (z[i] * 2 + z[i + 1]) * h)) * d + y[i];
end;
// akima m,t テーブル作成
// x[] xデーター配列
// y[] yデーター配列
// m[] m係数テーブル
// t[] t係数テーブル
procedure akima_table;
var
ii, n : integer;
a, b, half : double;
begin
n := high(x) + 1;
half := 1 / 2; // 0.5
// shift data by + 2 in the array and compute the secants
// also calculate extrapolated and end point secants
// 傾斜α両端を除く Δy/Δx
for ii := 0 to n - 2 do
m[ii + 2] := (y[ii + 1] - y[ii]) / (x[ii + 1] - x[ii]);
// 端点傾斜処理
m[1] := 2 * m[2] - m[3];
m[0] := 2 * m[1] - m[2];
m[n + 1] := 2 * m[n] - m[n - 1];
m[n + 2] := 2 * m[n + 1] - m[n];
// 各ポイントの傾斜係数計算
for ii := 0 to n - 1 do begin
a := abs(m[ii + 3] - m[ii + 2]);
b := abs(m[ii + 1] - m[ii]);
if (a + b) <> 0 then
t[ii] := (a * m[ii + 1] + b * m[ii + 2]) / (a + b)
else
t[ii] := half * (m[ii + 2] + m[ii + 1]);
end;
end;
// akima 補間値計算
// xx xの値
// x[] xデーター配列
// y[] yデーター配列
// m[] m係数テーブル
// t[] t係数テーブル
// result 補間値y'
function akima_Interpolation(xx: double): double;
var
iB, iM, iT: integer;
a, b : double;
begin
iB := low(x); // x[] bottom 配列no
iT := high(x); // x[] top配列No
// xx値の上下の配列xの配列番号を探す
// XX<x[iB]の場合一番下の区間 XX>x[iT]の場合一番上の区間
while (iT - iB) > 1 do begin
iM := (iB + iT) div 2; // middle配列no
if x[iM] > xx then
iT := iM
else
iB := iM;
end;
b := x[iT] - x[iB]; // 区間のxの変化量
a := xx - x[iB]; // x[iB]からのxの値
// 3次akima spline 計算
result := y[iB]
+ t[iB] * a
+ (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a * a / b
+ (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a * a / (b * b);
end;
// 補間計算選択表示
procedure TForm1.ndisp;
begin
case radiogroup2.ItemIndex of
0 : Chart1.Title.Text.Text := 'Akima Spline Interpolation';
1 : Chart1.Title.Text.Text := 'Natural Spline Interpolation';
2 : Chart1.Title.Text.Text := 'Newtonian Interpolation';
3 : Chart1.Title.Text.Text := 'Linear interpolation';
end;
end;
// 選択補間計算
function Interpolation(xx: double): double;
begin
result := 0;
case Form1.radiogroup2.ItemIndex of
0 : result := akima_Interpolation(xx); // akima 補間計算
1 : result := spline(xx); // natural 補間計算
2 : result := interpolate(xx); // newton 補間計算
3 : result := Linear_interpolation(xx);
end;
end;
// グリッドの値による補間計算
procedure TForm1.interpolationBtnClick(Sender: TObject);
var
N, ch, i, imax : integer;
cn : string;
y2, y3 : double;
xx : double;
begin
Xin_interpolation.Enabled := False;
N := Ninput;
if N < 0 then exit;
setlength(x, N);
setlength(y, N);
setlength(m, N + 3); // Akima用
setlength(t, N); // Akima用
setlength(z, N); // natural用
setlength(nt, N); // newton用
setlength(lz, N - 1); // Linear用
for i := Low(x) to High(x) do begin
val(StringGrid1.cells[1,i + 1], x[i], ch);
if ch <> 0 then begin
cn := 'x' + intTostr(i + 1) + 'に間違いが有ります。';
application.MessageBox(pchar(cn),'注意',0);
break;
end;
val(StringGrid1.cells[2,i + 1], y[i], ch);
if ch <> 0 then begin
cn := 'y' + intTostr(i + 1) + 'に間違いが有ります。';
application.MessageBox(pchar(cn),'注意',0);
break;
end;
end;
if ch <> 0 then exit;
if not datacheck(x, N) then exit; // xの値に重複が無いか確認
Series1.Clear; // プロット値
Series2.Clear; // テスト計算値
Series3.Clear; // 補間値
Series4.Clear; // テスト値と補間値差分
Series5.Clear; // 指定点計算値
xmin := x[0];
xmax := x[0];
for i := Low(x) to High(x) do begin
if x[i] > xmax then xmax := x[i];
if x[i] < xmin then xmin := x[i];
Series1.AddXY(x[i], y[i]); // データーポイント表示
nt[i] := y[i]; // newton用テーブル作成用にコピー
end;
akima_table; // akima テーブル作成
maketable; // natural テーブル作成
Newtonian_maketabler; // newton テーブル作成
Linear_maketable; // Linear テーブル作成
ndisp; // 選択補間名表示
imax := N * 20; // 分割数
dx := (xmax - xmin) / imax;
y2 := 0;
for i := 0 to imax do begin
xx := i * dx + x[0]; // x'
y3 := Interpolation(xx); // 補間計算
Series3.AddXY(xx, y3);
if DEF then begin
case radiogroup1.ItemIndex of
0 : y2 := f(xx);
1 : y2 := f1(xx);
2 : y2 := f2(xx);
end;
Series2.AddXY(xx, y2); // テスト値
Series4.AddXY(xx, y3 - y2); // 差分値 差分値-テスト値
end;
end;
DEF := False;
Xin_interpolation.Enabled := True;
end;
// 指定値からの計算 指定値xによるy補間値計算とグラフ表示
procedure TForm1.Xin_interpolationClick(Sender: TObject);
var
ch, i, j : integer;
xd, y1, y3, xx, gmin, gmax: double;
begin
val(Xedit.Text, xd, ch);
if ch <> 0 then begin
application.MessageBox('xからY推定の入力に間違いが有ります。','注意',0);
exit;
end;
Series2.Clear; // テスト値グラフ
Series3.Clear; // 補間値グラフ
Series4.Clear; // 差分値
Series5.Clear; // 指定値点
ndisp; // 選択補間名表示
// 最小最大区間グラフ再描画
gmin := xmin;
gmax := xmax;
if xd < xmin then gmin := xd;
if xd > gmax then gmax := xd;
i := round((gmax - gmin) / dx);
for j := 0 to i do begin
xx := j * dx + gmin; // x'
y3 := Interpolation(xx); // 補間計算
Series3.AddXY(xx, y3);
end;
// 指定値点グラフ追加 指定値xによるy補間値計算とグラフ表示
y1 := Interpolation(xd); // 補間計算
Series5.AddXY(xd, y1);
end;
// グリッド初期設定
procedure TForm1.FormCreate(Sender: TObject);
begin
FGridSet(101, 3); // 固定行1列1 + 100行2列まで行列を変更しても
// 入力値がクリアされないようにします。
GridSet(4, 3); // 最初の設定
end;
end.
akima_Spline_Interpolation.zip
三角関数、逆三角関数、その他関数 に戻る