
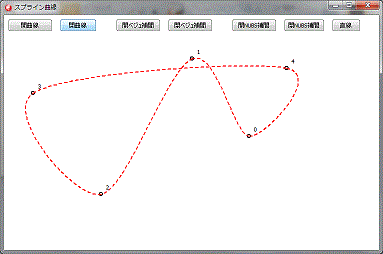
指定点通過自由曲線
自由曲線の描画は、画像処理とは少し違うのですが、画像への描画ということで、此処で取り上げてみました。
delphiには、指定点を通過する曲線の描画メソッドはありません。
又、線の種類(破線、一点鎖線、二点鎖線)は、線幅1以外は実線となってしまいます。
指定点を通る、曲線は無限に存在することになるらしいのですが、代表的なものを探してみました。
曲線となるには、最低、指定点として三点が必要ですが、三点の場合、二次曲線で結ぶ事が事が出来、円で繋ぐ事も可能です。
そこで、四点を結ぶ曲線を考え、三点の場合は、二点が同じ座標と考えることにします。
しかし、自分で、指定点を通る曲線の方程式を解くのは能力がなく、難しいので、インターネットで探した結果、Delphiでのプログラムを公開しているホームページ afsoft を見つけたので、参考にさせて頂きました。
CADのプログラムを作る場合の、参考になるように作られていて、単に曲線を描くには、不向きなので、曲線の計算プログラムは、そのままコピーさせて頂き、描画のルーチンだけ少し変更しました。
ノンユニフォームBスプライン補間、スプラインベジェ補間、カーディナルスプラインの三種類です。
実際に、プログラムに組み込む場合は、どれか一種類あれば、十分でしょう。
afsoft
は、最近更新されていないようなので、必要な情報があったら、今のうちに、アクセスして、取り込んでおいたほうが良いでしょう。
afsoftのサンプルプログラムは、Delphi6で作成されているので、DelphiXEで実行する場合、何も変更しないでも、そのまま実行することが可能です。
次の実行画面は、指定点通過曲線の部分を取り出して作り直したものです。
ダウンロードしたプログラムの実行画面ではありません。
自由曲線描画用のボタンをクリックすると、乱数により通過点を発生、曲線を描画します。
閉曲線の場合は、始点の座標と、終点の座標を同じにすると同時に、開か閉かの指定を行います。
ノンユニフォームBスプライン補間、スプラインベジェ補間の場合は、制御点の計算のため、ガウスジョルダン法で連立方程式を解いています。


上図は、開曲線と、閉曲線を実行した例です。
プログラム
// 作図 image1.Canvas.Pen.Width := lw; case ls of 0: image1.Canvas.Pen.Style := psDash; 1: image1.Canvas.Pen.Style := psDashDot; 2: image1.Canvas.Pen.Style := psDashDotDot; 3: image1.Canvas.Pen.Style := psSolid; end; // 線幅によるピッチの補正 // pitchControl(ls, lw); dp := 0; d1 := 0; for i := 0 to num - 2 do begin x0 := vx[i]; y0 := vy[i]; x1 := qx[(i * 2 + 1) * m1 - 1]; y1 := qy[(i * 2 + 1) * m1 - 1]; x2 := qx[(i * 2 + 2) * m1 - 1]; y2 := qy[(i * 2 + 2) * m1 - 1]; x3 := vx[i + 1]; y3 := vy[i + 1]; t := 0.0; BezierSub(px1, py1, t, x0, x1, x2, x3, y0, y1, y2, y3); image1.Canvas.MoveTo(round(px1), round(py1)); for j := 1 to sp do begin t := t + 1.0 / sp; BezierSub(px2, py2, t, x0, x1, x2, x3, y0, y1, y2, y3); image1.Canvas.LineTo(round(px2), round(py2)); // LineSubPitch(ls, dp, d1, px1, py1, px2, py2); // px1 := px2; // py1 := py2; end; end;
上記プログラムは下記プログラムの SplineBezier の描画の部分を修正したもので、通常の MoveTo LineTo
を使用して線の描画をしています。
線の太さが1で良い場合は、LineSubPitch のルーチンを使用する必要はありません。
Windows API の
ExtCreatePenで、線の太さ、線のスタイルの設定は出来ますが、曲線に使用することは出来ません。
次のプログラム例では
LineSubPitch pitchControl には 印刷の設定はありません。
印刷時の解像度に合わせて、ピッチ配列の値を大きくするルーチンを追加する必要があります。
又、図形の大きさに合わせて、指定点区間の分割数を大きくする必要もあります。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.ExtCtrls, Vcl.StdCtrls, Math;
type
TForm1 = class(TForm)
Button1: TButton;
Image1: TImage;
Button2: TButton;
Button3: TButton;
Button4: TButton;
Button5: TButton;
Button6: TButton;
Button7: TButton;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
procedure Button4Click(Sender: TObject);
procedure Button5Click(Sender: TObject);
procedure Button6Click(Sender: TObject);
procedure Button7Click(Sender: TObject);
private
{ Private 宣言 }
procedure ImgeClear;
procedure CardinalSpline(lf, lw, oc, sp, num: integer; av: double; vx, vy: array of double);
procedure SplineSub(var xp, yp: double; t, av, x0, x1, x2, x3, y0, y1, y2, y3: double);
procedure LineSub(px1, py1, px2, py2: double);
procedure SplineBezier(ls, lw, oc, sp, num: integer; vx, vy: array of double);
procedure gauss(m, n: integer; var a: array of double);
procedure BezierSub(var xp, yp: double; t, x1, x2, x3, x4, y1, y2, y3, y4: double);
procedure nonUniFormBSpline(ls, lw, oc, sp, num: integer; vx, vy: array of double);
function Dist(x1, y1, x2, y2: double): double ;
procedure SplineSub2(tn, nmax: integer; t: double; var tv, bn: array of double);
procedure SplineSub3(tn, nmax, kai: integer; t: double; var tv, bn1, bn2: array of double);
function Angle(dx, dy:double): double ;
procedure LineSubPitch(Ln: integer; var i: integer; var d1: double; px1, py1, px2, py2: double);
procedure pitchControl(NLine, LW: integer);
procedure pass_point(oc, num: integer; vx, vy: array of double);
procedure StraightLine(lf, lw: integer; x1, y1, x2, y2: double);
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
const
PitchN = 5; // 線ピッチ設定数
LineN = 3; // 線種数
LIMIT8 = 0.00000001;
type
TLinePitch = Record // 線種用レコード
Pitch : array[0..PitchN] of double; // ピッチ 線長さ 空白の繰り返し
segment : integer; // ピッチ数
End;
var
lx, ly : array of double; // x, y 座標
n : integer; // 指定座標点数
pn : integer; // 描画分割数
av : double; // 曲率係数
LPitch : array of TLinePitch;
VPitch : array[0..PitchN] of double;
//-------------
// 画像全消去
//-------------
procedure TForm1.ImgeClear;
var
Rect : TRect;
begin
Rect.Top := 0;
Rect.Left := 0;
Rect.Right := image1.Width;
Rect.Bottom := image1.Height;
image1.Canvas.Brush.Color := clWhite;
image1.Canvas.Brush.Style := bsSolid;
Image1.Canvas.FillRect(Rect);
end;
//------------------------------
// 通過点表示
//------------------------------
procedure TForm1.pass_point(oc, num: integer; vx, vy: array of double);
var
i : integer;
begin
image1.Canvas.Pen.Style := psSolid;
image1.Canvas.Pen.Width := 2;
// 通過点は番号表示
for i := 0 to num - 1 do begin
if (oc = 0) and (i = num - 1) then break;
image1.Canvas.TextOut(round(vx[i] + 10), round(vy[i] - 20), inttostr(i));
end;
// 通過点丸表示
image1.Canvas.Brush.Style := bsClear;
image1.Canvas.pen.Color := clBlack;
for i := 0 to num - 1 do begin
image1.Canvas.Ellipse(round(vx[i] - 4), round(vy[i] - 4), round(vx[i] + 4), round(vy[i] + 4));
end;
end;
//---------------------------------------------------
// ガウス・ジョルダン法によるn元1次連立方程式の解
// m : 横
// n : 縦(次数)
// a : 行列(n*m) m:1,2,・・・×n:1,2,・・・
//---------------------------------------------------
procedure TForm1.gauss(m , n: integer; var a: array of double);
const
LIMIT10 = 0.0000000001;
var
i, j, k : integer;
t : double;
begin
for k := 0 to m - 2 do begin
j := k ;
t := abs(a[k]);
for i := k + 1 to n - 1 do begin
if t < Abs(a[k + i * m]) then begin
t := Abs(a[k + i * m]);
j := i;
end;
end;
if j > k then begin
for i := 0 to m - 1 do begin
t := a[i + k * m];
a[i + k * m] := a[i + j * m];
a[i + j * m] := t;
end;
end;
//
t := a[k + k * m];
if Abs(t) > LIMIT10 then begin // ゼロによる除算防止
for i := k to m - 1 do
a[i + k * m] := a[i + k * m] / t;
end;
for j := 0 to n - 1 do begin
if j = k then continue;
t := a[k + j * m];
for i := k to m-1 do begin
a[i + j * m] := a[i + j * m] - a[i + k * m] * t;
end;
end;
end;
end;
//----------------------------
// 二点間線引き
//----------------------------
procedure TForm1.LineSub(px1, py1, px2, py2: double);
var
x1, y1, x2, y2 : integer ;
begin
x1 := Round(px1);
y1 := Round(py1);
x2 := Round(px2);
y2 := Round(py2);
image1.Canvas.MoveTo(x1, y1);
image1.Canvas.LineTo(x2, y2);
end;
//----------------------
// 距離(長さ)を計算
// x1, y1 : 始点
// x2, y2 : 終点
// out : 距離(長さ)
//----------------------
function TForm1.Dist(x1, y1, x2, y2 : double): double;
begin
Result := Sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1));
end;
//--------------------------------
// 角度を計算[rad]
// dx : X方向差分
// dy : Y方向差分
// out: 角度 (0~2 * Pi)
//--------------------------------
function TForm1.Angle(dx, dy: double): double;
var
r : double ;
begin
Result := 0.0;
if (Abs(dx) < LIMIT8) and (Abs(dy) < LIMIT8) then exit;
r := ArcTan2(dy, dx);
if r < 0.0 then r := r + 2.0 * Pi;
Result := r;
end;
//-----------------------------------------------
// 線幅によるピッチの補正
// 線幅を広くするとスペースが狭くなるので広げます
// NLine 線種
//-----------------------------------------------
procedure TForm1.pitchControl(NLine, LW: integer);
var
i : integer;
begin
// 線幅によるピッチの補正
for i := 0 to pitchN do begin
if i mod 2 <> 0 then // 奇数配列noセグメントがスペース
Vpitch[i] := LPitch[NLine].Pitch[i] + LW // スペースに線幅加算
else
Vpitch[i] := LPitch[NLine].Pitch[i];
end;
end;
//--------------------------------------
// 線分の表示・サブ2:線種指定
// Ln : 線種番号(1-)
// i : 開始セグメント番号(終了時更新)
// d1 : 開始ピッチ長さ (終了時更新)
// px1, py1 : 線分始点[mm]
// px2, py2 : 線分終点[mm]
//--------------------------------------
procedure TForm1.LineSubPitch(Ln: integer; var i: integer; var d1: double; px1, py1, px2, py2: double);
var
x1, y1, x2, y2 : double;
a, sa, ca, d, p : double;
PenStyle : TPenstyle;
begin
PenStyle := Image1.Canvas.Pen.Style; // 線種バックアップ
Image1.Canvas.Pen.Style := psSolid;
if (Ln < 0) or (Ln >= LineN) then begin // 無い線種は実線
LineSub(px1, py1, px2, py2);
Image1.Canvas.Pen.Style := PenStyle; // 線種戻し
exit;
end;
a := Angle(px2 - px1, py2 - py1); // 角度計算
d := Dist(px1, py1, px2, py2); // 距離計算
ca:= Cos(a); // コサイン
sa:= Sin(a); // サイン
x1:= px1; // 始点x
y1:= py1 ; // 始点y
repeat
p := Vpitch[i] - d1; // ピッチと開始ピッチ長さ差分 残り分
if (p > d) then p := d; // 距離より残り分が大きい場合 距離
x2 := x1 + p * ca ; // 新しい位置計算
y2 := y1 + p * sa ;
if (i mod 2) = 0 then // セグメント偶数毎に線引き 空白部線引きしない
LineSub(x1, y1, x2, y2);
x1 := x2; // 終点を始点にセット
y1 := y2;
d := d - p; // 残り長さ計算
if d > LIMIT8 then begin // 残り長さがあったら
d1 := 0.0; // 開始ピッチ長さクリア
Inc(i); // セグメントカウンターインクリメント
if i >= LPitch[Ln].segment then i := 0; // セグメント数を超えたらゼロに戻し
end;
until d <= LIMIT8;
d1 := d1 + p; // 開始ピッチ長さ
Image1.Canvas.Pen.Style := PenStyle; // 線種戻し
end;
//-----------------------------------------
// 直線の描画
// lf 線の種類
// lw 線の幅
// x1, y1 始点
// x2, y2 終点
//-----------------------------------------
procedure TForm1.StraightLine(lf, lw: integer; x1, y1, x2, y2 : double);
var
i : integer;
d1 : double;
begin
image1.Canvas.Pen.Width := lw;
image1.Canvas.Pen.Color := clBlack;
// 線幅によるピッチの補正
pitchControl(lf, lw);
i := 0;
d1 := 0;
// 線描画
LineSubPitch(lf, i, d1, x1, y1, x2, y2);
end;
//------------------------------------------------------------------
// スプライン曲線の表示 サブ3
// de boor-coxの漸化式によるBスプライン基底関数のn次微係数の計算
//------------------------------------------------------------------
procedure TForm1.SplineSub3(tn, nmax, kai: integer; t: double; var tv, bn1, bn2: array of double);
var
i, j : integer;
a0, a1, a2 : double;
begin
for j := 0 to nmax - 1 do
bn2[j] := 0.0;
for i := 1 to kai - 1 do begin
for j := 0 to nmax - 1 do begin
a1 := 0.0;
a2 := 0.0;
a0 := tv[j + (i + 1) - 1] - tv[j];
if Abs(a0) > LIMIT8 then
a1 := bn1[j + nmax * (i - 1)] / a0;
a0 := tv[j + i + 1] - tv[j + 1];
if Abs(a0) > LIMIT8 then
a2 := bn1[j + 1 + nmax * (i - 1)] / a0;
bn2[j + nmax * i] := i * (a1 - a2);
end;
end;
end;
//-------------------------------------------------------
// スプライン曲線の表示 サブ2
// de boor-coxの漸化式によるBスプライン基底関数の計算
//-------------------------------------------------------
procedure TForm1.SplineSub2(tn , nmax: integer; t: double; var tv, bn: array of double);
var
i, j, k : integer;
a0, a1, a2 : double;
begin
k := 0;
for i := 0 to nmax - 1 do bn[i] := 0.0;
for i := 0 to nmax - 1 do begin
if (tv[i] - LIMIT8 <= t) and (t < tv[i + 1] - LIMIT8) then begin
bn[i] := 1.0;
k := i;
end;
end;
if (tv[nmax - 1] - LIMIT8 <= t) and (t <= tv[nmax] + LIMIT8) then begin
bn[nmax - 1] := 1.0;
k := nmax - 1;
end;
for i := 1 to 3 do begin
for j := 0 to nmax - 1 do bn[j + nmax * i] := 0.0;
for j := k - i to k do begin
a1 := 0.0;
a2 := 0.0;
a0 := tv[j + (i + 1) - 1] - tv[j];
if Abs(a0) > LIMIT8 then
a1 := (t - tv[j]) * bn[j + nmax * (i - 1)] / a0;
a0 := tv[j + (i + 1)] - tv[j + 1] ;
if Abs(a0) > LIMIT8 then
a2 := (tv[j + (i + 1)] - t) * bn[j + 1 + nmax * (i - 1)] / a0;
bn[j + nmax * i] := a1 + a2;
end;
end;
end;
//-----------------------------------------------
// ノンユニフォームBスプライン補間
// oc 1 開曲線 0 閉曲線
// sp 通過点間分割数
// num 通過点数
// vx vy 通過点配列
// ls 線の種類
// lw 線の幅
//-----------------------------------------------
procedure TForm1.nonUniFormBSpline(ls, lw, oc, sp, num: integer; vx, vy: array of double);
var
i, j : integer;
t : double;
x0, x1, x2, x3 : double;
y0, y1, y2, y3 : double;
px1, px2 : double;
py1, py2 : double;
//
m1, m2 : integer ;
qx, qy : array of double;
//
qn : integer; // 制御点の数
jisu : integer; // 次数
kai : integer; // 階数
tn : integer; // ノットベクトルの数
tv : array of double; // ノットベクトル
nmax : integer; // 基底関数の数
bn : array of double; // 基底関数
bn1 : array of double; // 基底関数の1次微係数
bn2 : array of double; // 基底関数の2次微係数
d : double ;
maxq, jj : integer ;
q, x, y : array of double;
dp : integer;
d1 : double;
begin
// NUBS(ノンユニフォームBスプライン曲線)補間
qn := num + 2;
jisu := 3;
kai := jisu + 1;
tn := qn + kai ;
// ノットベクトル
SetLength(tv, tn);
tv[0] := 0.0;
tv[1] := 0.0;
tv[2] := 0.0;
tv[3] := 0.0;
t := 0.0 ;
for i := 0 to num - 2 do begin
d := Dist(vx[i], vy[i], vx[i + 1], vy[i + 1]);
t := t + d ;
tv[4 + i] := t;
end;
tv[3 + num] := tv[2 + num];
tv[4 + num] := tv[2 + num];
tv[5 + num] := tv[2 + num];
//
nmax := qn ;
SetLength(bn , nmax * 4);
SetLength(bn1, nmax * 4);
SetLength(bn2, nmax * 4);
SetLength(qx, qn * (qn + 1));
SetLength(qy, qn * (qn + 1));
for i := 0 to qn * (qn + 1) - 1 do begin
qx[i] := 0.0;
qy[i] := 0.0;
end;
// Bスプライン基底関数 -> 通過点 -> 制御点
for i := 0 to num - 1 do begin
t := tv[i + jisu] ;
SplineSub2(tn, nmax, t, tv, bn);
for j := 0 to nmax - 1 do begin
qx[j + i * (qn + 1)] := bn[j + nmax * 3];
qy[j + i * (qn + 1)] := bn[j + nmax * 3];
end;
qx[nmax + i * (qn + 1)] := vx[i];
qy[nmax + i * (qn + 1)] := vy[i];
end;
if oc = 1 then begin
// 開曲線=両端の曲率=0=2次微分値=0
i := 0;
t := tv[i + jisu] ;
SplineSub2(tn, nmax, t, tv, bn);
SplineSub3(tn, nmax, kai, t, tv, bn, bn1);
SplineSub3(tn, nmax, kai, t, tv, bn1, bn2);
for j := 0 to nmax - 1 do begin
qx[j + num * (qn + 1)] := bn2[j + nmax * 3];
qy[j + num * (qn + 1)] := bn2[j + nmax * 3];
end;
qx[nmax + num *(qn + 1)] := 0.0;
qy[nmax + num *(qn + 1)] := 0.0;
i := num - 1;
t := tv[i + jisu];
SplineSub2(tn, nmax, t, tv, bn);
SplineSub3(tn, nmax, kai, t, tv, bn , bn1);
SplineSub3(tn, nmax, kai, t, tv, bn1, bn2);
for j := 0 to nmax - 1 do begin
qx[j + (num + 1) * (qn + 1)] := bn2[j + nmax * 3];
qy[j + (num + 1) * (qn + 1)] := bn2[j + nmax * 3];
end;
qx[nmax + (num + 1) * (qn + 1)] := 0.0;
qy[nmax + (num + 1) * (qn + 1)] := 0.0;
end
else begin
// 閉曲線=両端の曲率が同じ=差=0=2次微分値の差=0
// 両端の接線が同じ=差=0=1次微分値の差=0
i := 0;
t := tv[i + jisu];
SplineSub2(tn, nmax, t, tv, bn);
SplineSub3(tn, nmax, kai, t, tv, bn , bn1);
SplineSub3(tn, nmax, kai, t, tv, bn1, bn2);
for j := 0 to nmax - 1 do begin
qx[j + num * (qn + 1)] := bn2[j + nmax * 3];
qy[j + num * (qn + 1)] := bn2[j + nmax * 3];
qx[j + (num + 1) * (qn + 1)] := bn1[j + nmax * 3];
qy[j + (num + 1) * (qn + 1)] := bn1[j + nmax * 3];
end;
i := num - 1;
t := tv[i + jisu];
SplineSub2(tn, nmax, t, tv, bn);
SplineSub3(tn, nmax, kai, t, tv, bn , bn1);
SplineSub3(tn, nmax, kai, t, tv, bn1, bn2);
for j := 0 to nmax - 1 do begin
qx[j + num * (qn + 1)] := qx[j + num * (qn + 1)] - bn2[j + nmax * 3];
qy[j + num * (qn + 1)] := qy[j + num * (qn + 1)] - bn2[j + nmax * 3];
qx[j + (num + 1) * (qn + 1)] := qx[j + (num + 1) * (qn + 1)] - bn1[j + nmax * 3];
qy[j + (num + 1) * (qn + 1)] := qy[j + (num + 1) * (qn + 1)] - bn1[j + nmax * 3];
end;
qx[nmax + num * (qn + 1)] := 0.0;
qy[nmax + num * (qn + 1)] := 0.0;
qx[nmax + (num + 1) * (qn + 1)]:= 0.0;
qy[nmax + (num + 1) * (qn + 1)]:= 0.0;
end;
// 行列式を解く
gauss(qn + 1, qn, qx);
gauss(qn + 1, qn, qy);
// 各区間毎に描画設定を行う 配列确保
maxq := (jisu + 1) + kai; // 1区間分
SetLength(q, maxq);
SetLength(x, jisu + 1);
SetLength(y, jisu + 1);
image1.Canvas.Pen.Color := clBlue;
image1.Canvas.Pen.Width := lw;
// 線幅によるピッチの補正
pitchControl(ls, lw);
dp := 0;
d1 := 0;
for j := 0 to (num - 2) do begin
// ノットベクトル
for i := 0 to (maxq - 1) do
q[i] := tv[i+j];
// 制御点
for i := 0 to jisu do begin
x[i] := qx[qn + (i + j) * (qn + 1)];
y[i] := qy[qn + (i + j) * (qn + 1)];
end;
px1 := 0.0;
py1 := 0.0;
t := q[kai - 1];
for i := 0 to sp - 1 do begin
px2 := 0.0;
py2 := 0.0;
for jj:=0 to kai - 1 do begin
SplineSub2(maxq, kai + 2, t, q, bn);
px2 := px2 + bn[jj + (kai + 2) * 3] * x[jj];
py2 := py2 + bn[jj + (kai + 2) * 3] * y[jj];
end;
if i > 0 then
LineSubPitch(ls, dp, d1, px1, py1, px2, py2);
px1 := px2;
py1 := py2;
t := t + (q[kai] - q[kai - 1]) * 1.0 / sp;
end;
// 最後の線引き
LineSubPitch(ls, dp, d1, px1, py1, vx[j + 1], vy[j + 1]);
end;
//
q := nil;
x := nil;
y := nil;
tv := nil;
bn := nil;
bn1 := nil;
bn2 := nil;
qx := nil;
qy := nil;
end;
//-------------------------
// ベジェ曲線の表示 サブ
//-------------------------
procedure TForm1.BezierSub(var xp, yp: double; t, x1, x2, x3, x4, y1, y2, y3, y4: double);
var
t0, t1, t2, t3 : double;
tm1 : double;
begin
tm1 := 1.0 - t;
t0 := tm1 * tm1 * tm1;
t1 := 3.0 * t * tm1 * tm1;
t2 := 3.0 * tm1 * t * t;
t3 := t * t * t;
xp := t0 * x1 + t1 * x2 + t2 * x3 + t3 * x4;
yp := t0 * y1 + t1 * y2 + t2 * y3 + t3 * y4;
end;
//-----------------------------------------------
// スプラインベジェ補間
// oc 1 開曲線 0 閉曲線
// sp 通過点間分割数
// num 通過点数
// vx vy 通過点配列
// ls 線の種類
// lw 線の幅
//-----------------------------------------------
procedure TForm1.SplineBezier(ls, lw, oc, sp, num: integer; vx, vy: array of double);
var
i, j: integer;
t : double;
x0, x1, x2, x3 : double;
y0, y1, y2, y3 : double;
px1, px2 : double;
py1, py2 : double;
m1, m2 : integer ;
qx, qy : array of double;
dp : integer;
d1 : double;
begin
// ベジェ補間
// 途中の制御点を算出するための行列を生成
m1 := (num - 1) * 2 + 1;
m2 := (num - 1) * 2;
SetLength(qx, m1 * m2);
SetLength(qy, m1 * m2);
for i := 0 to m1 * m2 - 1 do
qx[i] := 0.0;
for i := 0 to num - 3 do begin
qx[(i * 2 ) * m1 + i * 2 + 1] := 1.0;
qx[(i * 2 ) * m1 + i * 2 + 2] := 1.0;
qx[(i * 2 + 1) * m1 + i * 2 ] := 1.0;
qx[(i * 2 + 1) * m1 + i * 2 + 1] := -2.0;
qx[(i * 2 + 1) * m1 + i * 2 + 2] := 2.0;
qx[(i * 2 + 1) * m1 + i * 2 + 3] := -1.0;
end;
if oc = 1 then begin
// 開曲線
qx[((num - 2) * 2 ) * m1 ] := 2.0;
qx[((num - 2) * 2 ) * m1 + 1 ] := -1.0;
qx[((num - 2) * 2 + 1) * m1 + (num - 2) * 2 ] := -1.0;
qx[((num - 2) * 2 + 1) * m1 + (num - 2) * 2 + 1] := 2.0;
end
else begin
// 閉曲線
qx[((num - 2) * 2 ) * m1 ] := 1.0;
qx[((num - 2) * 2 ) * m1 + (num - 2) * 2 + 1] := 1.0;
qx[((num - 2) * 2 + 1) * m1 ] := 2.0;
qx[((num - 2) * 2 + 1) * m1 + 1 ] := -1.0;
qx[((num - 2) * 2 + 1) * m1 + (num - 2) * 2 ] := 1.0;
qx[((num - 2) * 2 + 1) * m1 + (num - 2) * 2 + 1] := -2.0;
end;
for i := 0 to m1 * m2 - 1 do
qy[i] := qx[i];
// 行列に座標値をセット
for i := 0 to num - 3 do begin
qx[(i * 2 + 1) * m1 - 1] := 2.0 * vx[i + 1];
qy[(i * 2 + 1) * m1 - 1] := 2.0 * vy[i + 1];
end;
if oc = 1 then begin
// 開曲線
qx[((num - 2) * 2 + 1) * m1 - 1] := vx[0];
qy[((num - 2) * 2 + 1) * m1 - 1] := vy[0];
qx[((num - 2) * 2 + 2) * m1 - 1] := vx[num - 1];
qy[((num - 2) * 2 + 2) * m1 - 1] := vy[num - 1];
end
else begin
// 閉曲線
qx[((num - 2) * 2 + 1) * m1 - 1] := 2.0 * vx[num - 1];
qy[((num - 2) * 2 + 1) * m1 - 1] := 2.0 * vy[num - 1];
end;
// 行列を解く
gauss(m1, m2, qx);
gauss(m1, m2, qy);
// 作図
image1.Canvas.Pen.Width := lw;
// 線幅によるピッチの補正
pitchControl(ls, lw);
dp := 0;
d1 := 0;
for i := 0 to num - 2 do begin
x0 := vx[i];
y0 := vy[i];
x1 := qx[(i * 2 + 1) * m1 - 1];
y1 := qy[(i * 2 + 1) * m1 - 1];
x2 := qx[(i * 2 + 2) * m1 - 1];
y2 := qy[(i * 2 + 2) * m1 - 1];
x3 := vx[i + 1];
y3 := vy[i + 1];
t := 0.0;
BezierSub(px1, py1, t, x0, x1, x2, x3, y0, y1, y2, y3);
for j := 1 to sp do begin
t := t + 1.0 / sp;
BezierSub(px2, py2, t, x0, x1, x2, x3, y0, y1, y2, y3);
LineSubPitch(ls, dp, d1, px1, py1, px2, py2);
px1 := px2;
py1 := py2;
end;
end;
qx := nil;
qy := nil;
end;
//-------------------------------
// カーディナルスプライン サブ
// xp, yp 計算結果座標
// t 分割計算店
// av 曲率
// x0, x1, x2, x3 X座標4点
// y0, y1, y2, y3 Y座標4点
//-------------------------------
procedure TForm1.SplineSub(var xp, yp: double; t, av, x0, x1, x2, x3, y0, y1, y2, y3:double);
var
t0, t1, t2, t3, dx1, dy1, dx2, dy2 : double;
begin
t0 := 2.0 * t * t * t - 3.0 * t * t + 1.0;
t1 := -2.0 * t * t * t + 3.0 * t * t;
t2 := t * t * t - 2.0 * t * t + t;
t3 := t * t * t - t * t;
dx1 := av * (x2 - x0);
dy1 := av * (y2 - y0);
dx2 := av * (x3 - x1);
dy2 := av * (y3 - y1);
xp := t0 * x1 + t1 * x2 + t2 * dx1 + t3 * dx2;
yp := t0 * y1 + t1 * y2 + t2 * dy1 + t3 * dy2;
end;
//-----------------------------------------------
// カーディナルスプライン曲線
// oc 1 開曲線 0 閉曲線
// sp 通過点間分割数
// num 通過点数
// av 曲線係数
// vx vy 通過点配列
// lf 線の種類
// lw 線の幅
//-----------------------------------------------
procedure TForm1.CardinalSpline(lf, lw, oc, sp, num: integer; av: double; vx, vy: array of double);
var
i, j : integer;
px1, py1 : double; // 線開始点
px2, py2 : double; // 線終点
t : double; // 分割計算点
x0, x1, x2, x3 : double; // 通過点x座標
y0, y1, y2, y3 : double; // 通過点y座標
dp : integer;
d1 : double;
begin
image1.Canvas.Pen.Width := lw; // 線幅
image1.Canvas.Pen.Color := clRed; // 線の色
// 線幅によるピッチの補正
pitchControl(lf, lw);
// 通過点曲線計算と線描画
for i := 0 to num - 2 do begin
if i > 0 then begin
x0 := vx[i - 1];
y0 := vy[i - 1];
end
else begin
if oc = 1 then begin
// 開曲線
x0 := vx[0];
y0 := vy[0];
end
else begin
// 閉曲線
x0 := vx[num - 2];
y0 := vy[num - 2];
end;
end;
x1 := vx[i];
y1 := vy[i];
x2 := vx[i + 1];
y2 := vy[i + 1];
if i < num - 2 then begin
x3 := vx[i + 2];
y3 := vy[i + 2];
end
else begin
if oc = 1 then begin
// 開曲線
x3 := vx[i + 1];
y3 := vy[i + 1];
end
else begin
// 閉曲線
x3 := vx[1];
y3 := vy[1];
end;
end;
// 最初の座標点計算
t := 0.0; // 位置0
SplineSub(px1, py1, t, av, x0, x1, x2, x3, y0, y1, y2, y3); // 座標点計算
// 分割計算と線描画
d1 := 0;
dp := 0;
for j := 1 to sp do begin // 分割数分繰り返し
t := t + 1.0 / sp; // 計算点加算
SplineSub(px2, py2, t, av, x0, x1, x2, x3, y0, y1, y2, y3); // 座標計算
LineSubPitch(lf, dp, d1, px1, py1, px2, py2);
px1 := px2; // 終点Xを開始点Xへ
py1 := py2; // 終点Yを開始点yへ
end;
end;
end;
//-----------------------------------
// カーディナルスプライン開曲線描画
//-----------------------------------
procedure TForm1.Button1Click(Sender: TObject);
var
i, lf, lw , oc: integer;
begin
n := 5; // 指定点数
pn := 30; // 点間分割数
setlength(lx, n); // x位置配列確保
setlength(ly, n); // y位置配列确保
for i := 0 to n - 1 do begin // 指定位置座標設定
lx[i] := Random(550) + 50;
ly[i] := Random(350) + 65;
end;
ImgeClear; // 描画部クリア
// 通過点表示
oc := 1;
pass_point(oc, n, lx, ly);
av := 0.5; // 曲線係数
// 線の種類 線の幅ランダム設定
lf := Random(4); // 線の種類は四種類 >= 3 は実線
lw := Random(4) + 1; // 線の幅
// 曲線描画
CardinalSpline(lf, // 線種
lw, // 線幅
1, // 開曲線
pn, // 区間分割数
n, // 通過点数
av, // 曲線係数
lx, // 通過点X座標配列
ly // 通過点Y座標配列
);
end;
//-------------------------------
// カーディナルスプライン閉曲線描画
//-------------------------------
procedure TForm1.Button2Click(Sender: TObject);
var
i, lf, lw, oc: integer;
begin
n := 6;
pn := 30;
setlength(lx, n);
setlength(ly, n);
for i := 0 to n - 2 do begin
lx[i] := Random(550) + 50;
ly[i] := Random(350) + 65;
end;
lx[n - 1] := lx[0]; // 閉曲線はスタートとエンドが同じ座標
ly[n - 1] := ly[0]; // 閉曲線はスタートとエンドが同じ座標
oc := 0; // 閉曲線
// 線の種類 線の幅ランダム設定
lf := Random(4); // 線の種類は四種類 >= 3 は実線
lw := Random(4) + 1; // 線の幅
ImgeClear;
// 通過点表示
pass_point(oc, n, lx, ly);
av := 0.5; // 曲線係数
// 曲線描画
CardinalSpline(lf, // 線種
lw, // 線幅
oc, // 閉曲線
pn, // 区間分割数
n, // 通過点数
av, // 曲線係数
lx, // 通過点X座標配列
ly // 通過点Y座標配列
);
end;
//-------------------------------
// ベジェ補間開曲線描画
//-------------------------------
procedure TForm1.Button3Click(Sender: TObject);
var
i, oc: integer;
begin
n := 5;
pn := 30;
setlength(lx, n);
setlength(ly, n);
for i := 0 to n - 1 do begin
lx[i] := Random(500) + 75;
ly[i] := Random(300) + 90;
end;
oc := 1; // 開曲線
ImgeClear;
// 通過点表示
pass_point(oc, n, lx, ly);
// 曲線描画
SplineBezier( 1, // 一点鎖線
1, // 線幅
oc, // 開閉曲線
pn, // 区間分割数
n, // 通過点数
lx, // 通過点X座標配列
ly // 通過点Y座標配列
);
end;
//-------------------------------
// ベジェ補間閉曲線描画
//-------------------------------
procedure TForm1.Button4Click(Sender: TObject);
var
i, oc: integer;
begin
n := 6;
pn := 30;
setlength(lx, n);
setlength(ly, n);
for i := 0 to n - 2 do begin
lx[i] := Random(500) + 75;
ly[i] := Random(300) + 90;
end;
lx[n - 1] := lx[0]; // 閉曲線はスタートとエンドが同じ座標
ly[n - 1] := ly[0]; // 閉曲線はスタートとエンドが同じ座標
oc := 0; // 閉曲線
ImgeClear;
// 通過点表示
pass_point(oc, n, lx, ly);
// 曲線描画
SplineBezier( 0, // 線種破線
2, // 線幅
oc, // 閉開曲線
pn, // 区間分割数
n, // 通過点数
lx, // 通過点X座標配列
ly // 通過点Y座標配列
);
end;
//--------------------------------------
// ノンユニフォームBスプライン開曲線描画
//--------------------------------------
procedure TForm1.Button5Click(Sender: TObject);
var
i, oc: integer;
begin
n := 5;
pn := 30;
setlength(lx, n);
setlength(ly, n);
for i := 0 to n - 1 do begin
lx[i] := Random(500) + 75;
ly[i] := Random(300) + 90;
end;
oc := 1; // 開曲線
ImgeClear;
// 通過点表示
pass_point(oc, n, lx, ly);
// 曲線描画
nonUniFormBSpline( 1, // 線種一点鎖線
1, // 線幅
oc, // 開閉曲線
pn, // 区間分割数
n, // 通過点数
lx, // 通過点X座標配列
ly // 通過点Y座標配列
);
end;
//--------------------------------------
// ノンユニフォームBスプライン閉曲線描画
//--------------------------------------
procedure TForm1.Button6Click(Sender: TObject);
var
i, oc: integer;
begin
n := 6;
pn := 30;
setlength(lx, n);
setlength(ly, n);
for i := 0 to n - 2 do begin
lx[i] := Random(500) + 75;
ly[i] := Random(300) + 90;
end;
lx[n - 1] := lx[0]; // 閉曲線はスタートとエンドが同じ座標
ly[n - 1] := ly[0]; // 閉曲線はスタートとエンドが同じ座標
oc := 0; // 閉曲線
ImgeClear;
// 通過点表示
pass_point(oc, n, lx, ly);
// 曲線描画
nonUniFormBSpline( 0, // 線種破線
2, // 線幅
oc, // 閉開曲線
pn, // 区間分割数
n, // 通過点数
lx, // 通過点X座標配列
ly // 通過点Y座標配列
);
end;
//-----------------------------------
// 直線の描画
//-----------------------------------
procedure TForm1.Button7Click(Sender: TObject);
var
x1, x2 : double;
y1, y2 : double;
lf : integer;
lw : integer;
begin
// 線の種類 線の幅ランダム設定
lf := Random(4); // 線の種類は四種類 >= 3 は実線
lw := Random(4) + 1; // 線の幅
x1 := Random(200) + 50;
x2 := Random(200) + 450;
y1 := Random(400) + 50;
y2 := Random(400) + 50;
ImgeClear;
StraightLine(lf, // 線種
lw, // 線幅
x1, // 始点X座標
y1, // 始点Y座標
x2, // 終点X座標
y2 // 終点Y座標
);
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
ClientWidth := 750;
ClientHeight := 470;
// 線種配列确保
setlength(LPitch, LineN);
// 線種データーセット
LPitch[0].segment := 2; // 破線
LPitch[0].Pitch[0] := 6;
LPitch[0].Pitch[1] := 3;
LPitch[1].segment := 4; // 1点鎖線
LPitch[1].Pitch[0] := 15;
LPitch[1].Pitch[1] := 3;
LPitch[1].Pitch[2] := 3;
LPitch[1].Pitch[3] := 3;
LPitch[2].segment := 6; // 2点鎖線
LPitch[2].Pitch[0] := 18;
LPitch[2].Pitch[1] := 3;
LPitch[2].Pitch[2] := 3;
LPitch[2].Pitch[3] := 3;
LPitch[2].Pitch[4] := 3;
LPitch[2].Pitch[5] := 3;
end;
end.
Delphi Users' Forum
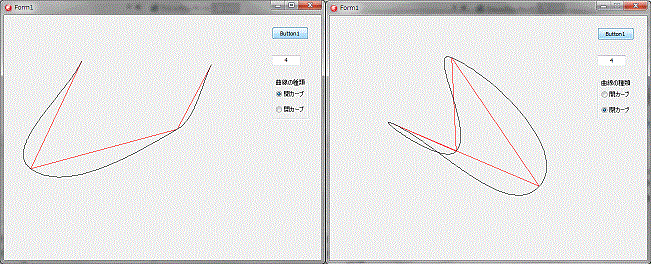
に折れ線からペジェスプライン変換のプログラムがあったので、テストしてみました。
下図、左側の開曲線の場合、制御点の計算方法により、始点と終点部で、直線に近くなるような傾向を示し、少し違和感があるような、感じになります。
閉曲線の場合は、問題ないようです。
単に曲線が必要なだけなら、問題は無いでしょう。
プログラム
unit Unit1;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
OcRadio: TRadioGroup;
LabeledEdit1: TLabeledEdit;
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
type TDPoint = record
x: double;
y: double;
end;
type TDp4 = record
x1, y1: double;
x2, y2: double;
x3, y3: double;
x4, y4: double;
end;
///////////////////////////////////////////////////
// 4点を与えてp0~p1の範囲のベジェ点化して返す
function BezierCvt(pr, p0, p1, p2: TDPoint): TDp4;
const
MIND = 0.1;
var
dx, dy, k, r, b:double;
begin
k := 0.3; // kは 0.1~0.3の範囲 小さい程折線に近い
with Result do begin
x1 := p0.x;
y1 := p0.y;
x4 := p1.x;
y4 := p1.y;
dx := x4 - x1;
dy := y4 - y1;
r := K * sqrt(dx * dx + dy * dy);
// x2,y2 は p0点からpr-p1直線延長上距離rの点
dx := p1.x - pr.x;
dy := p1.y - pr.y;
b := sqrt(dx * dx + dy * dy);
// ゼロで除算するのを防止します
if b > MIND then begin
x2 := x1 + r * dx / b;
y2 := y1 + r * dy / b;
end
else begin
x2 := x1 + r * dx / MIND;
y2 := y1 + r * dy / MIND;
end;
// x3,y3 は p1点からp2-p0直線延長上距離rの点
dx := p0.x - p2.x;
dy := p0.y - p2.y;
b := sqrt(dx * dx + dy * dy);
// ゼロで除算するのを防止します
if b > MIND then begin
x3 := x4 + r * dx / b;
y3 := y4 + r * dy / b;
end
else begin
x3 := x4 + r * dx / MIND;
y3 := y4 + r * dy / MIND;
end;
end;
end;
///////////////////////////////////////////////////
// ベジェ点データqを与えてその区間 t=0~1 で点を返す
function BezierData(q: TDp4; t: double): TDpoint;
var
v : double;
v3, v2 : double;
t3, t2 : double;
begin
v := 1 - t;
v3 := v * v * v;
v2 := 3 * v * v;
t3 := t * t * t;
t2 := 3 * t * t;
with Result do with q do begin
x := v3 * x1 + v2 * t * x2 + v * t2 * x3 + t3 * x4;
y := v3 * y1 + v2 * t * y2 + v * t2 * y3 + t3 * y4;
end;
end;
///////////////////////////////////////////////////
// Form1 画面クリア
procedure clearForm1;
begin
with Form1.Canvas do begin
Brush.Style := bsSolid;
Brush.Color := clBtnface;
FillRect(rect(0, 0, Form1.ClientWidth, Form1.ClientHeight));
end;
end;
///////////////////////////////////////////////////
//呼び出し方のサンプル
// 始点、終点では 始点終点を重ねるだけで、まあまあの結果が得られます。
// なお、 閉曲線なら始点終点を互いに重ねるだけの事です。
procedure TForm1.Button1Click(Sender: TObject);
var
i, j, k : integer;
q : TDp4;
dd : array of TDpoint;
n, sp : integer;
begin
clearForm1;
// 通過点
val(LabeledEdit1.Text, n ,K);
if K <> 0 then begin
application.MessageBox('通過点数が整数ではありません。','通過点数',0);
exit;
end;
if N < 2 then begin
application.MessageBox('通過点数が少なすぎます。','通過点数',0);
exit;
end;
// 通過点の配列 閉曲線は 通過点に対して二個多く
// 開曲線は三個多くします
case OcRadio.ItemIndex of
0 : Setlength(dd, n + 2); // 開曲線
1 : Setlength(dd, n + 3); // 閉曲線
end;
// 通過点の生成 乱数でセット
// 配列の二番目の位置からn個
for i := 1 to n do begin
dd[i].x := Random(400) + 50;
dd[i].y := Random(300) + 50;
end;
// dd[1]~dd[n] が通過点 dd[0],dd[n+1],dd[n+2] はベジェ計算用追加通過点
k := n; // 線を引く回数
case OcRadio.ItemIndex of
0 : begin // 開曲線
dd[0].x := dd[1].x; // 最初の通過点二個同じ値
dd[0].y := dd[1].y;
dd[n + 1].x := dd[n].x; // 最後の通過点二個同じ値
dd[n + 1].y := dd[n].y;
end;
1 : begin // 閉曲線
dd[0].x := dd[n].x; // 配列最初に最後の通過点をセット
dd[0].y := dd[n].y;
dd[n + 1].x := dd[1].x; // 最後に最初の点と次の通過点をセット
dd[n + 1].y := dd[1].y;
dd[n + 2].x := dd[2].x;
dd[n + 2].y := dd[2].y;
k := n + 1; // 線を引く回数 閉曲線の場合は1多く
end;
end;
sp := 100; // 作図分割数
with Canvas do begin
// 通過点折れ線表示
Pen.color:=clRed;
MoveTo(round(dd[1].x),round(dd[1].y));
for i := 2 to k do LineTo(round(dd[i].x),round(dd[i].y));
// ベジェ曲線表示
Pen.color := clBlack;
for i := 1 to k - 1 do begin
// 四点から制御点計算
q := BezierCvt(dd[i - 1], dd[i], dd[i + 1], dd[i + 2]) ;
// 分割点の座標を計算し曲線を描画
if i = 1 then MoveTo(round(q.x1), round(q.y1));
for j := 1 to sp do
with BezierData(q, j / sp) do LineTo(round(x), round(y));
end;
end;
end;
end.
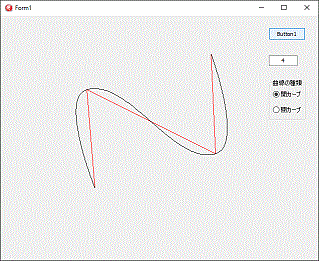
前記プログラムの、開曲線の始点と終点の部分が直線に近づく事を修正してみました。
開曲線の時、最初のデーターと、最後のデーターを二つ同じものを並べていたために、発生している現象なので、これを修正してみました。
一番最初のデーターを最初の通過指定点と同じ座標にするのではなく、二つ目の通過指定点と同じ座標にします。
最後のデーターは、最後の通過指定点にするのではなく、ひとつ前の通過点にすることで、自然な曲線の始まりと、終わりを描画することが出来ます。
最初と、最後の制御点の方向が、最初及び最後の直線方向と同じにならないようにしています。
プログラム
前のプログラムの変更点だけ載せています。
// dd[1]~dd[n] が通過点 dd[0],dd[n+1],dd[n+2] はベジェ計算用追加通過点 k := n; // 線を引く回数 case OcRadio.ItemIndex of 0 : begin // 開曲線 dd[0].x := dd[2].x; // 二番目の通過点を最初のデーターにします。 dd[0].y := dd[2].y; dd[n + 1].x := dd[n - 1].x; // 最後から二番目の通過点を最後のデーターにします。 dd[n + 1].y := dd[n - 1].y; end; 1 : begin // 閉曲線 dd[0].x := dd[n].x; // 配列最初に最後の通過点をセット dd[0].y := dd[n].y; dd[n + 1].x := dd[1].x; // 最後に最初の点と次の通過点をセット dd[n + 1].y := dd[1].y; dd[n + 2].x := dd[2].x; dd[n + 2].y := dd[2].y; k := n + 1; // 線を引く回数 閉曲線の場合は1多く end; end;