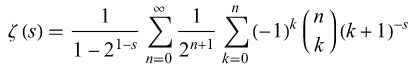
リーマンゼータ関数 続き
二項係数を利用した計算です。
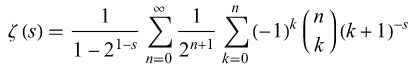
ｎの値無限大迄積分する計算式ですが、演算精度Double程度で有れば、ｎ=70～80程度で十分な精度を確保出来ます。
ｓの値がゼロより小さい場合は、正しい値を計算できないので、下記の計算式を使用します。
これは前の、リーマンゼータ関数と同じですが、-側用の計算式を用いないときの-側の誤差は、前のものより大きくなります。
プログラムは、前のものより簡単です。
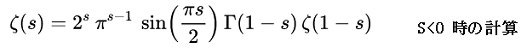
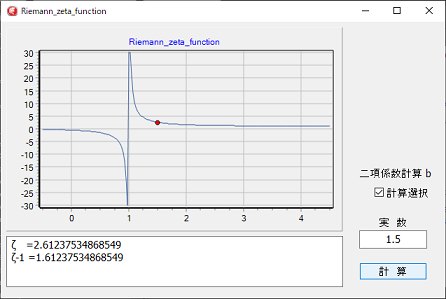二項係数の計算方法の選択ができる様になっていますが、計算結果は変わりません。
二項係数の選択ができるプログラムには、ｓの値がマイナスの時のプログラムは組み込まれていません。
プログラム s<0の時のルーチン無
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, Vcl.StdCtrls,
Vcl.ExtCtrls, VCLTee.Series, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart;
type
TForm1 = class(TForm)
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
Memo1: TMemo;
LabeledEdit1: TLabeledEdit;
Button1: TButton;
CheckBox1: TCheckBox;
Label1: TLabel;
procedure Button1Click(Sender: TObject);
procedure CheckBox1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses math;
// 二項係数a
function combi(n, r: integer): double;
var
i : integer;
c : double;
begin
c := 1;
if (r >= 1) and (r < n) then begin
for i := 1 to r do
c := c * ((n + 1 - i) / i);
end;
result := c;
end;
// 二項係数b
function binomial(n, k: integer): double;
var
i : integer;
z : double;
begin
z := 1;
if k = 0 then begin
result := z;
exit;
end;
i := k;
repeat
z := z * n;
dec(k);
if n > 1 then dec(n);
until k < 1;
repeat
z := z / i;
dec(i);
until i < 2;
result := z;
end;
// リーマンゼータ関数
function Riemann_zeta(s: double): double;
const
NMAX = 80;
var
t, x, y, z : double;
n, k : integer;
begin
if s = 1 then begin
result := infinity;
exit;
end;
z := 0; // Σn=0,∞ クリア
for n := 0 to NMAX do begin // ∞の代わりにNMAX
t := 1 / power(2, n + 1);
y := 0; // Σk=0,n クリア
for k := 0 to n do begin
if Form1.CheckBox1.Checked = false then
x := combi(n, k) * power(k + 1, -s) // {n,k}(k+1)^-s
else
x := binomial(n, k) * power(k + 1, -s); // {n,k}(k+1)^-s
if k mod 2 = 1 then x := -x; // -1^k
y := y + x; // Σk=0,n
end;
t := t * y; // (Σk=0,n)/(2^(n+1))
z := z + t; // Σn=0.∞
end;
z := z / (1 - power(2, 1 - s)); // (Σn=0.∞)/(1-2^(1-s)
result := z;
end;
procedure TForm1.Button1Click(Sender: TObject);
var
inx, ans, xmin, xmax, dx, x, y : double;
ch, i : integer;
begin
val(labelededit1.Text, inx, ch);
if ch <> 0 then begin
application.MessageBox('入力値に間違いがあります。','注意',0);
exit;
end;
ans := Riemann_zeta(inx);
memo1.Clear;
memo1.Lines.Append('ζ =' + floattostr(ans));
memo1.Lines.Append('ζ-1 =' + floattostr(ans - 1));
series1.Clear;
series2.Clear;
// if ans > 30 then ans := 30;
// if ans < -30 then ans := -30;
series2.AddXY(inx, ans);
xmax := inx + 3;
xmin := inx - 2;
dx := (xmax - xmin) / 200;
for i := 0 to 200 do begin
x := i * dx + xmin;
y := Riemann_zeta(x);
// if y > 30 then y := 30;
// if y < -30 then y := -30;
series1.AddXY(x, y);
end;
end;
procedure TForm1.CheckBox1Click(Sender: TObject);
begin
if CheckBox1.Checked = false then Label1.Caption := '二項係数計算 a'
else Label1.Caption := '二項係数計算 b';
end;
end.
プログラム s<0 時の修正あり
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, Vcl.StdCtrls,
Vcl.ExtCtrls, VCLTee.Series, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart;
type
TForm1 = class(TForm)
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
Memo1: TMemo;
LabeledEdit1: TLabeledEdit;
Button1: TButton;
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses math;
function Gamma(x: double): double; // ガンマ関数
const
M = 8; // ベルヌーイ数の配列数
//ベルヌーイ数B(2)、B(4)、B(6)、...、B(16)
B : array[1..M] of double = ( 1.0 / 6, // B(2)
-1.0 / 30,
1.0 / 42,
-1.0 / 30,
5.0 / 66,
-691.0 / 2730,
7.0 / 6,
-3617.0 / 510); // B(16)
var
i : integer;
sum, xx, v, xj, lng : double;
begin
sum := 0;
v := 1;
while x < M do begin
v := v * x;
x := x + 1;
end;
lng := ln(sqrt(2 * pi)) - x + (x - 0.5) * ln(x) - ln(v);
xx := x * x;
xj := x;
for i := 1 to M do begin
sum := sum + B[i] / (i * 2 * (2 * i - 1)) / xj;
xj := xj * xx;
end;
result := exp(sum + lng);
end;
// 二項係数a
function binomial(n, r: integer): double;
var
i : integer;
c : double;
begin
c := 1;
if (r >= 1) and (r < n) then begin
for i := 1 to r do
c := c * ((n + 1 - i) / i);
end;
result := c;
end;
// リーマンゼータ関数
function XRiemann_zeta(s: double): double;
const
NMAX = 80;
var
t, x, y, z : double;
n, k : integer;
begin
if s = 1 then begin
result := infinity;
exit;
end;
z := 0; // Σn=0,∞ クリア
for n := 0 to NMAX do begin // ∞の代わりにNMAX
y := 0; // Σk=0,n クリア
for k := 0 to n do begin
x := binomial(n, k) * power(k + 1, -s); // {n,k}(k+1)^-s
if k mod 2 = 1 then x := -x; // -1^k
y := y + x; // Σk=0,n
end;
t := y / power(2, n + 1); // (Σk=0,n)/(2^(n+1))
z := z + t; // Σn=0.∞
end;
z := z / (1 - power(2, 1 - s)); // (Σn=0.∞)/(1-2^(1-s)
result := z;
end;
// リーマンゼータ関数 負数補正計算
function RiemannZeta(s: double): double;
var
term : double;
ints : integer;
def : double;
begin
ints := trunc(s);
def := s - ints;
if (s <= -2) and (def = 0) and (ints mod 2 = 0) then
result := 0
else
if s <= -1 then begin
term := power(2, s) * power(pi, s - 1) * sin(pi * s / 2);
result := term * XRiemann_Zeta(1 - s) * Gamma(1 - s);
end
else
result := XRiemann_Zeta(s);
end;
// 入力処理計算
procedure TForm1.Button1Click(Sender: TObject);
var
inx, ans, xmin, xmax, dx, x, y : double;
ch, i : integer;
begin
val(labelededit1.Text, inx, ch);
if ch <> 0 then begin
application.MessageBox('入力値に間違いがあります。','注意',0);
exit;
end;
ans := RiemannZeta(inx);
memo1.Clear;
memo1.Lines.Append('ζ =' + floattostr(ans));
memo1.Lines.Append('ζ-1 =' + floattostr(ans - 1));
series1.Clear;
series2.Clear;
if ans > 30 then ans := 30;
if ans < -30 then ans := -30;
series2.AddXY(inx, ans);
xmax := inx + 3;
xmin := inx - 2;
dx := (xmax - xmin) / 200;
for i := 0 to 200 do begin
x := i * dx + xmin;
y := RiemannZeta(x);
if y > 30 then y := 30;
if y < -30 then y := -30;
series1.AddXY(x, y);
end;
end;
end.
RiemannA_zeta_function.zip