二項係数計算の高速化計算に使用する素数の値検索
二項係数を素数を利用して高速に計算するプログラムに素数、或いは素数代替数を設定するプログラムです。
オイラー数の計算プログラムの中に、素数を利用して、割り算を掛け算に変更し、演算の高速化をはかるモードがあり、その計算に使用する素数或いは素数代替数の設定が必要となり、その値を求めるプログラムを作成しました。
二項係数は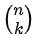
で表される値ですが、
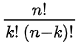で計算が可能です。
一つの値しか使用しない場合は、定数で与えてしまえばよいのですが 違う値で、繰り返し計算する場合は、階乗のテーブルを作成して、
bin
= f[n] / (f[k] * f[n-k]) で計算するのが一番簡単な方法です。
一番早いのは、n,kの配列を作成する方法です、bin =
f[n, k] となり演算の必要はなくなり一番高速となります。
しかし、この方法では、メモリーの使用量が多くなると同時に、使用されない無駄な配列領域が発生します。
そこまで、高速は必要ではないが、なるべく早く計算したい場合に、素数を使用して、演算に時間の掛かる割り算を、掛け算にして高速化をはかります。
素数を使用することにより、使用した素数より大きな値がなくなると同時に、割り算が掛け算になるので、計算が少し早くなります。
素数の値が 10^9 + 1 の時 int64(符号付き64ビット)では、n = 32, k = 16
が一番大きな値となります。
これより大きな n, k
値では、int64がオーバーフローするのですが、整数演算では、オーバーフローの検出が無い為、正しい値が計算出来ているような間違いをするので注意が必用です。
階乗での計算では、n = 20 迄で、これより大きくすると階乗の計算でint64がオーバーフローしますので、素数を利用した方が大きい値まで計算が可能です。
bigintegerの場合は、メモリーの上限に達しない限り、オーバーフローは発生しません。
素数利用のメリットは、演算する値の最大値をおさえる事ができ階乗での計算より大きな値が計算可能、n, k が大きい時の計算速度の向上で、
デメリットは、プログラムが少し長くなること、とn,k配列を使用した時ほど速度が速くならない事です。
此処のプログラムでは、素数を利用した時、使用する二項係数の値の最大値より大きく、一番近い値の素数を使用すると、bigintegerのメモリーの使用量、演算の値を小さくすることができ効率よく計算が出来るので、この素数、或いは素数代替数の値を求めます。
二項係数計算 1
この計算では、modp(mod64)は、必ずしも素数である必要性はありませんが正しく計算出来る値は探し出す必要があります。
const
mod64 = 1000000007; // 素数あるいは、素数代替数
var
fact64: array of int64;
fact64_inv: array of int64;
// 配列の作成 int64
procedure init64_nck(size: integer);
var
i: integer;
inv64: array of int64;
begin
setlength(fact64, size + 1);
setlength(fact64_inv, size + 1);
setlength(inv64, size + 1);
fact64[0] := 1;
fact64[1] := 1;
fact64_inv[0] := 1;
fact64_inv[1] := 1;
inv64[0] := 1;
inv64[1] := 1;
for i := 2 to size do begin
fact64[i] := fact64[i - 1] * i mod mod64; // 階乗
inv64[i] := mod64 - inv64[mod64 mod i] * (mod64 div i) mod mod64; // 逆数
fact64_inv[i] := fact64_inv[i - 1] * inv64[i] mod mod64; // 逆数の階乗
end;
end;
二項係数計算 2 フェルマーの小定理
modp(mod64)の値は素数でないと成り立ちません。
const
mod64 = 1000000007; // 素数
var
fact64: array of int64;
fact64_inv: array of int64;
function invcalc(x : int64): int64; // 逆数計算
var
res, k, y : int64;
begin
res := 1;
k := mod64 - 2;
y := x;
while K <> 0 do begin
if k and 1 = 1 then res := (res * y) mod mod64;
y := (y * y) mod mod64;
k := k div 2;
end;
result := res;
end;
procedure init(size: integer);
var
i : integer;
begin
setlength(fact64, size + 1);
setlength(fact64_inv, size + 1);
fact64[0] := 1;
for i := 1 to size do fact64[i] := (fact64[i - 1] * i) mod mod64; // 階乗
fact64_inv[size] := invcalc(fact64[size]); // 逆数
for i := size - 1 downto 0 do fact64_inv[i] := (fact64_inv[i + 1] * (i + 1)) mod mod64;
end;
一度、配列の作成をしてしまえば、Function で二項係数の値を求める事ができます。
// 二項係数
function binomialint64(n, k: integer): int64;
begin
result := fact64[n] * (fact64_inv[k] * fact64_inv[n - k] mod mod64) mod mod64;
end;
素数、或いは素数代替数の検索プログラム
素数、或いは、素数代替数の検索は素数候補の値で計算した二項係数計算1、2 と二項係数計算3の 配列[c, k]の値を比べて一致するかどうかで検索します。
二項係数計算 3
var
comint: array of array of int64; // nCk ck配列 int64
procedure calac_comint(size: integer);
var
i, j: integer;
begin
setlength(comint, size + 1, size + 1);
comint[0, 0] := 1;
for i := 1 to size do begin
comint[i, 0] := 1;
for j := 1 to size do
comint[i, j] := comint[i - 1, j - 1] + comint[i - 1, j];
end;
end;
二項係数計算1と二項係数計算3を使用した場合は、素数以外の素数代替数も検索されます。
二項係数計算2と二項係数計算3を使用した場合は、素数を検索することができます。
上記のプログラム例は、int64となっていますが、実際のプログラムでは、大きな値を扱う為、Bigintegerでプログラムが組まれています。
bigintegerの組み込みはベルヌーイ数 その４を参照してください。
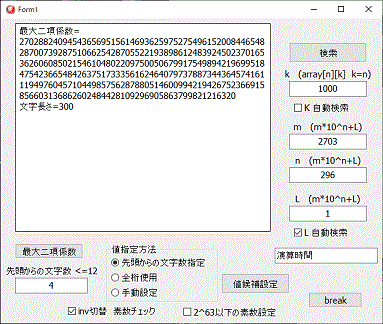配列を使用した値を基準に素数の検索を行うので、まず配列の大きさを設定し、"最大二項係数"のボタンをクリック、最大二項係数の値を表示させます。
次に、素数候補地の先頭の値の設定方法を選択、"候補地設定"ボタンをクリックしてm,n,Lの値を設定させます。
後は、Lの自動検索を行うか、inv逆数計算
素数か、等の設定をして検索ボタンをクリックすれば、modの計算に使用する、素数、素数代替数の検索が出来ます。
Lの自動検索をにチェックを入れない場合は、単に判定だけを行い、チェックを入れると、奇数に２を加算しながら、正解が見つかるまで計算を続けます。
K自動検索にチェックを入れると、素数候補として、設定された値に対して、小さくて一番近い最大値の二項係数の配列サイズKを自動的に検索してから、素数或いは素数代替数の判定
又は、:検索を行います。
配列のサイズが2000を超えると、演算時間が非常に長くなると同時に、メモリー不足にな場合があります。
2^63以下の素数判定は、int64以下の値の場合素数判定を行って検索するモードですが、検算とプログラムの確認用に用意したものです。
プログラム
// mod p による二項係数の計算の為にmod pの値を求める計算です。
// 計算式にもよりますが、pの値は必ずしも素数である必要が無いことは確認済みです。
// inv配列の計算式は、本プログラムによります。
// 素数以外の出力も可能な場合2^63 以下は素数の指定が出来ます。
// 2^63以上でも素数の指定が出来ますが演算に時間がかかります。
// 配列の大きさが2000を超えると、メモリー不足になることがありますPCの搭載メモリー量によります。
unit Unit1;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons,system.Diagnostics;
type
TForm1 = class(TForm)
BitBtn1: TBitBtn;
LabeledEdit1: TLabeledEdit;
Memo1: TMemo;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
LabeledEdit4: TLabeledEdit;
Edit1: TEdit;
BitBtn2: TBitBtn;
RadioGroup1: TRadioGroup;
LabeledEdit5: TLabeledEdit;
BitBtn3: TBitBtn;
CheckBox1: TCheckBox;
BitBtn4: TBitBtn;
CheckBox2: TCheckBox;
CheckBox3: TCheckBox;
CheckBox4: TCheckBox;
procedure BitBtn1Click(Sender: TObject);
procedure BitBtn2Click(Sender: TObject);
procedure BitBtn3Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure BitBtn4Click(Sender: TObject);
private
{ Private 宣言 }
function input(var k, m, n, l: int64): boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses Velthuis.BigIntegers, Velthuis.BigDecimals, system.Math;
var
modbig: biginteger;
fact: array of BigInteger;
fact_inv: array of BigInteger;
com: array of array of Biginteger; // nCk ck配列
f : array of BigInteger;
rf : array of BigInteger;
//------------------------------------------------------------------------------
// フェルマーの小定理
// 素数でないと正しい二項係数を返しません
// Modp 素数 modbig
function invcalc(x : biginteger): biginteger;
var
res, k, y : biginteger;
begin
res := 1;
k := modbig - 2;
y := x;
while K <> 0 do begin
if k and 1 = 1 then res := (res * y) mod modbig;
y := (y * y) mod modbig;
k := k div 2;
end;
result := res;
end;
// modp 逆数配列作成 modbig 素数
procedure init(size: integer);
var
i : integer;
begin
setlength(f, size + 1);
setlength(rf, size + 1);
f[0] := 1;
for i := 1 to size do f[i] := (f[i - 1] * i) mod modbig;
rf[size] := invcalc(f[size]);
for i := size - 1 downto 0 do rf[i] := (rf[i + 1] * (i + 1)) mod modbig;
end;
// 二項係数 BigInteger div 無し inv使用 n >= k
function binomial(n, k: integer): BigInteger;
begin
result := f[n] * (rf[k] * rf[n - k] mod modbig) mod modbig;
end;
//------------------------------------------------------------------------------
// inv配列の作成 Biginteger modbigは素数で無くても可
// 素数で無くても正しい二項係数を返しますが、値はなんでも良いわけではありません。
// 素数以外の場合は、正しい二項係数の値と全て比較して正しい答えのでる値です。
procedure init_nck(size: integer);
var
i : integer;
j : int64;
b : biginteger;
inv : array of BigInteger;
begin
setlength(fact, size + 1);
setlength(fact_inv, size + 1);
setlength(inv, size + 1);
fact[0] := 1;
fact[1] := 1;
fact_inv[0] := 1;
fact_inv[1] := 1;
inv[0] := 1; // 0でもok
inv[1] := 1;
for i := 2 to size do begin
fact[i] := fact[i - 1] * i mod modbig;
b := modbig mod i; // b < i
j := b.AsInt64; // biginteger -> 1nt64
inv[i] := modbig - inv[j] * (modbig div i) mod modbig;
fact_inv[i] := fact_inv[i - 1] * inv[i] mod modbig;
end;
end;
// 二項係数 BigInteger div 無し inv使用 n >= k
function binomialBig(n, k: integer): BigInteger;
begin
result := fact[n] * (fact_inv[k] * fact_inv[n - k] mod modbig) mod modbig;
end;
//------------------------------------------------------------------------------
// nCk C[n, k] 二項係数配列の作成
// 配列作成し値の最大値を返します
function calac_com(size: integer): biginteger;
var
i, j: integer;
begin
setlength(com, size + 1, size + 1);
result := 0;
com[0, 0] := 1;
for i := 1 to size do begin
com[i, 0] := 1;
for j := 1 to size do begin
com[i, j] := (com[i - 1, j - 1] + com[i - 1, j]);
if com[i, j] > result then result := com[i, j]; // 最大値
end;
end;
end;
//------------------------------------------------------------------------------
// 2^63以下の素数判定
function prime_check(n : int64): boolean;
var
c, s : int64;
begin
result := true;
if n <= 2 then begin result := False; exit; end;
s := trunc(sqrt(n)) + 1;
c := 3;
while c <= s do begin
if n mod c = 0 then begin
result := False;
break
end;
inc(c, 2);
end;
end;
//==============================================================================
var
maxfact : biginteger; // 二項係数最大値
maxf : string;
BreakF : boolean;
// 最大二項係数表示
procedure TForm1.BitBtn2Click(Sender: TObject);
var
ch, k : integer;
begin
val(labelededit4.Text, k , ch);
if ch <> 0 then begin
memo1.Text := 'kの値に間違いがあります。';
exit;
end;
if k < 0 then begin
memo1.Text := 'kの値はゼロより大きくしてください。';
exit;
end;
maxfact := calac_com(k);
k := length(maxfact.ToString);
memo1.Text := '最大二項係数= ' + maxfact.ToString;
memo1.Lines.Append('文字長さ=' + inttostr(k));
bitbtn3.Enabled := True;
end;
// 変数データーの入力
function TForm1.input(var k, m, n, l: int64): boolean;
var
ch : integer;
begin
result := false;
// 二項係数配列の大きさ
val(labelededit4.Text, k , ch);
if ch <> 0 then begin
memo1.Text := 'kの値に間違いがあります。';
exit;
end;
if k < 2 then begin
memo1.Text := 'kの値は2より大きくしてください。';
exit;
end;
// 候補先頭のm値 m * 10^n + L
val(labelededit3.Text, m , ch);
if ch <> 0 then begin
memo1.Text := 'mの値に間違いがあります。';
exit;
end;
if m < 0 then begin
memo1.Text := 'mの値はゼロより大きくしてください。';
exit;
end;
// 正解候補 m * 10^n + L のnの値
val(labelededit1.Text, n , ch);
if ch <> 0 then begin
memo1.Text := 'nの値に間違いがあります。';
exit;
end;
if n < 0 then begin
memo1.Text := 'nの値はゼロより大きくしてください。';
exit;
end;
// 正解候補 m * 10^n + L のLの値
val(labelededit2.Text, l , ch);
if ch <> 0 then begin
memo1.Text := 'Lの値に間違いがあります。';
exit;
end;
if l < 0 then begin
memo1.Text := 'Lの値はゼロより大きくしてください。';
exit;
end;
result := true;
end;
// 正解の候補確認
// 正解は素数でない場合がありますがinv(逆数)の二項係数は正しく計算出来る値です。
// 素数の計算も可能ですが大きな値は時間が掛かります。
// 素数で無くても可能な計算と素数が必要な計算ではInv逆数配列の計算が違います。
procedure TForm1.BitBtn1Click(Sender: TObject);
label
RS;
const
pch = 9223372036854775807; // 2^63 - 1
var
m, n, l, k : int64;
i, j : integer;
FactF : boolean;
madF : Byte;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
Loop : integer;
pmo : int64;
chbig : biginteger;
kback : integer;
begin
if not input(k, m, n, l) then exit;
StopWatch := TStopwatch.StartNew;
Loop := 0;
memo1.Clear;
edit1.Text := '演算中';
BreakF := False;
Kback := -1;
RS: // 再検索位置
application.ProcessMessages;
if (RadioGroup1.ItemIndex = 0) or (RadioGroup1.ItemIndex = 2) then // 文字数指定
modbig := biginteger.Pow(biginteger.Ten, n) * m + l;
if RadioGroup1.ItemIndex = 1 then begin // 手動入力
modbig := maxf;
modbig := modbig + l;
end;
if modbig < 3 then begin
memo1.Text := '候補の値が小さすぎます。';
exit;
end;
bitbtn1.Enabled := False;
Checkbox3.Enabled := False;
// mod候補値による配列のサイズの設定
if kback <> k then maxfact := calac_com(k); // 二項係数配列の作成 kの値が変わらなければ再計算しない
if checkbox4.Checked = True then begin // 配列のサイズ自動設定だったら
// 正解候補の大きさによってモードフラグ設定
if maxfact >= modbig then madF := 5 // 正解候補が小さい 5
else madF := 3; // 大きい 3
repeat // 候補値に配列の大きさを合わせる
if maxfact >= modbig then begin // 候補が小さい場合
if madF = 5 then begin // 小さいからスタートした場合配列のサイズ5小さく
k := k - 5;
if k < 2 then k := 2; // kの最小値は2
end;
if madF = 4 then begin // 小さいからスタートした場合
k := k - 1; // 候補が小さい場合1戻し
madf := 0; // 終了フラグ
end;
if (madF = 3) or (madF = 2) then begin // 大きいからスタートした場合配列の
k := k - 1; // サイズ1小さく
madF := 2; // 1小さくしているフラグセット
end;
end
else begin // 候補が大きい場合
if (madF = 5) or (madF = 4) then begin // 小さいからスタート配列のサイズ1大きく
k := k + 1; // サイズ1大きく
madF := 4; // 1大きくしているフラグセット
end;
if madF = 3 then K := K + 5; // 大きいからスタート配列のサイズ5大きく
if madF = 2 then madF := 0; // madF = 2だったら終了
end;
maxfact := calac_com(k);
if BreakF then break; // 打ち切りフラグで終了
application.ProcessMessages;
until (maxfact < modbig) and (madF = 0);
if BreakF then begin // 打ち切り表示
memo1.Text := '計算が打ち切られました。';
bitbtn1.Enabled := true;
Checkbox3.Enabled := true;
exit;
end;
end
else begin // 自動設定でない場合
if maxfact >= modbig then begin
memo1.Text := 'mod候補値より二項係数の値が大きいです。';
memo1.Lines.Append('候補値を大きくするか、k(配列)の値を小さくしてください。');
bitbtn1.Enabled := true;
Checkbox3.Enabled := true;
exit;
end;
end;
kback := k;
// mod値の検索 正解でなかったら候補値に2加算して再確認します
if checkbox3.Checked = False then init_nck(k) // 候補によるinv配列作成
else init(k);
labelededit4.Text := intTostr(k); // kの値表示
// memo1.Text := '最大二項係数= ' + maxfact.ToString;
memo1.Text := '確認中';
edit1.Text := '演算中';
application.ProcessMessages;
// 候補の正解確認
FactF := True;
for i := 0 to k do begin // 正解候補によるinv配列とcom配列の値比較
for j := 0 to i do begin
if checkbox3.Checked = False then chbig := binomialBig(i, j)
else chbig := binomial(i, j);
if chbig <> com[i][j] then begin // inv配列とcom配列が一致しなかったら
FactF := False; // 非正解フラグセット
memo1.Text := '正解ではありません。';
break;
end;
end;
if BreakF then break; // 打ち切りフラグで終了
application.ProcessMessages;
end;
if BreakF then begin // 打ち切り表示
memo1.Text := '計算が打ち切られました。';
bitbtn1.Enabled := true;
Checkbox3.Enabled := true;
exit;
end;
// 正解不正解の処理 不正解だっら2加算 再計算
if not FactF and checkbox1.Checked = True then begin // 正解でなく自動設定だったら
inc(Loop);
if l mod 2 = 0 then l := l - 1; // 末尾加算値が偶数だったら奇数にする
l := l + 2; // 末尾加算値に2加算
Labelededit2.Text := intTostr(l); // 加算値表示
if Loop < 10000 then goto RS // 再検索
else Memo1.Text := 'Loop数が 10000に達したので打ち切りました。A';
end;
// Bigintegerでの検索終了処理 正解無し の場合処理なし
if FactF then begin
// 2^63以下で素数設定だったら素数確認 素数でなかったら2加算再計算
if (modbig <= pch) and (checkbox2.Checked = True) then begin
val(modbig.ToString, pmo, i); // 1nt64に変換
// 素数確認 int64
if not prime_check(pmo) then begin // 素数でなかったら
if checkbox1.Checked = True then begin // 自動計算だったら
inc(Loop);
l := l + 2; // 末尾加算値に2加算
Labelededit2.Text := intTostr(l); // 加算値表示
if Loop < 1000 then goto RS // 再検索
else Memo1.Text := 'Loop数が 1000に達したので打ち切りました。B';
end
else begin
memo1.Text := '正解です。';
memo1.Lines.Append(modbig.ToString); // 正解表示
end;
end
else begin
memo1.Text := '素数です';
memo1.Lines.Append(modbig.ToString); // 素数表示
end;
end
else begin
// 2^63以上だったら終了 或いは素数確認でなかったら終了
if checkbox3.Checked = False then memo1.Text := '正解です。'
else memo1.Text := '素数です。';
memo1.Lines.Append(modbig.ToString); // 正解表示
end;
end;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
Edit1.text := '演算時間 = ' + intTostr(ElapsedMillseconds) + 'msec';
bitbtn1.Enabled := true;
Checkbox3.Enabled := true;
end;
// 正解候補の設定
procedure TForm1.BitBtn3Click(Sender: TObject);
var
ch : integer;
lg : integer;
lng : integer;
lsttr : string;
num : int64;
begin
// 指定された文字数を取り出し、整数化 1加算して正解候補先頭数字にします。
// 先頭数字以外は全てゼロ。
// 偶数なので、Labelededit2の奇数の値を加算して正解候補とします。
if RadioGroup1.ItemIndex = 0 then begin
val(LabeledEdit5.Text, lg, ch);
if ch <> 0 then begin
application.MessageBox('先頭からの文字数指定に間違いが有ります。','注意',0);
exit;
end;
if (lg < 1) or (lg > 12) then begin
application.MessageBox('文字数指定は1～12迄にしてください。','注意',0);
exit;
end;
maxf := maxfact.ToString; // 二項係数の最大値の文字列
lng := length(maxf); // 文字長さ
if lng > lg then begin // 文字長さより指定文字数が大きかったら
lsttr := copy(maxf, 1, lg); // 先頭から指定文字数取り出し
val(lsttr, num, ch); // 先頭文字数値変換
inc(num); // 先頭数値に1加算
Labelededit3.Text := intTostr(num); // 正解候補先頭のm値 m * 10^n + L
Labelededit1.Text := intTostr(lng - lg); // 指数nの値 m * 10^n + L
Labelededit2.Text := '1'; // 加算値Lの値 m * 10^n + L
Labelededit3.Enabled := True;
Labelededit1.Enabled := True;
end
else begin
application.MessageBox('指定文字数に足りません。','注意',0);
exit;
end;
end;
// 二項係数最大値をそのまま正解候補とします。
// 二項係数最大値は偶数なので、Labelededit2の奇数の値を加算して正解候補とします。
if RadioGroup1.ItemIndex = 1 then begin
maxf := maxfact.ToString; // 正解候補値
Labelededit3.Enabled := False;
Labelededit1.Enabled := False;
Labelededit2.Text := '1'; // 正解候補加算値
end;
if RadioGroup1.ItemIndex = 2 then begin
Labelededit3.Enabled := True;
Labelededit1.Enabled := True;
end;
bitbtn1.Enabled := True;
Checkbox3.Enabled := true;
end;
// 演算打ち切り フラグセット
procedure TForm1.BitBtn4Click(Sender: TObject);
begin
breakF := True;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
bitbtn1.Enabled := False;
bitbtn3.Enabled := False;
memo1.Text := '二項係数計算の為のmod値検索';
end;
end.
prime_number.zip
各種プログラム計算例に戻る