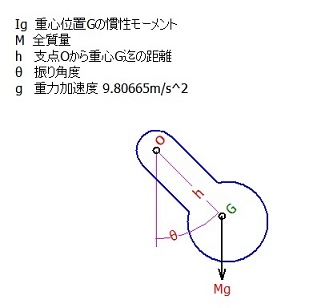
Ｉｇは振り子の腕の部分も含む全体の重心位置中心の慣性モーメントです。M質量も全体の質量となります。
hは振り子の支点Ｏから重心Ｇ迄の距離です。
振り子は支点Ｏを中心に振れるので、支点Oの慣性モーメントIoを計算して周期の計算をします。
Io = Ig + Mh2
Ioを単振り子の長さlに換算します。
l = Io / (Mh)
周期Tは
T = 4×√(l /g)×K
k = sin(θ/2) 離心率
Kは第一種完全楕円積分
周期Tの計算は、単振り子の計算と同じです。
実体振子(物理振子、剛体振子)
単振り子の周期に、慣性モーメントを持たない、理論的な振り子の周期計算がありますが、此処では、実際に形のある振り子の計算をします。
Ｉｇは振り子の腕の部分も含む全体の重心位置中心の慣性モーメントです。
M質量も全体の質量となります。
hは振り子の支点Ｏから重心Ｇ迄の距離です。
振り子は支点Ｏを中心に振れるので、支点Oの慣性モーメントIoを計算して周期の計算をします。
Io = Ig + Mh2
Ioを単振り子の長さlに換算します。
l = Io /
(Mh)
周期Tは
T = 4×√(l /g)×K
k = sin(θ/2) 離心率
Kは第一種完全楕円積分
周期Tの計算は、単振り子の計算と同じです。
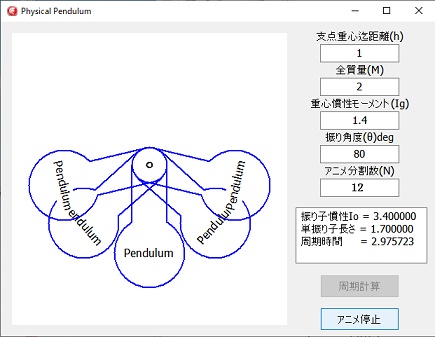左図は、プログラムの実行画面です。
重力加速度は、9.80665m/s2となっているので、長さの単位はmです。
アニメーションによる周期は、計算上の周期より長くなります。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Image1: TImage;
Button1: TButton;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
LabeledEdit4: TLabeledEdit;
Memo1: TMemo;
LabeledEdit5: TLabeledEdit;
Button2: TButton;
Timer1: TTimer;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Timer1Timer(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
procedure drawArc(r, x, y, st, ed:double; w: integer; c: Tcolor);
procedure drawPendulum(Q: double; F: boolean);
procedure drawLine(xs, ys, xe, ye: double; w: integer; c: Tcolor);
procedure drawtext(x, y: double; str: string; h: integer; Q: double);
procedure ImageClear;
function Elip1AGM(k: double): double;
function calcQ(L, st, k: double): double;
function Jacobi_sn(u, k: double): double;
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses
System.Math;
const
G = 9.80665; // 重力加速度
var
x0, y0 : integer; // image 作図原点座標
T : double; // 周期時間
AQ : array of double; // 角度配列
N : integer; // 分割数
DBL_EPSILON : double; // 桁落ち判定値
TN : integer; // アニメカウンター
Q : double; // 振り角度
ERF : boolean; // アニメ消去フラグ
QT : double; // アニメ角度
// Jacobi関数 Jacobi sn(u, k)
function TForm1.Jacobi_sn(u, k: double): double;
const
KN = 30;
var
a: array of double;
g: array of double;
c: array of double;
two_n : integer;
phi : double;
half : double;
i, j : integer;
begin
half := 1 / 2;
if k = 0 then begin
result := sin(u);
exit;
end;
if k = 1 then begin
result := sin(2 * arctan(exp(u)) - pi / 2);
exit;
end;
setlength(a, KN + 1);
setlength(g, KN + 1);
setlength(c, KN + 1);
a[0] := 1;
g[0] := sqrt(1 - k * k);
c[0] := k;
two_n := 1;
for i := 0 to KN do begin // 収束しなかった時KNで終了
if abs(a[i] - g[i]) < a[i] * DBL_EPSILON then break;
two_n := two_n + two_n;
a[i + 1] := half * (a[i] + g[i]);
g[i + 1] := sqrt(a[i] * g[i]);
c[i + 1] := half * (a[i] - g[i]);
end;
phi := two_n * a[i] * u;
for j := i downto 1 do
phi := half * (phi + arcsin(c[j] * sin(phi) / a[j]));
result := sin(phi);
end;
// 第一種完全楕円積分 算術幾何平均
function TForm1.Elip1AGM(k: double): double;
var
a, b, y : double;
da, db : double;
begin
a := 1;
b := sqrt(1 - k * k);
da := a - b;
db := 0;
while da <> db do begin
db := da;
y := a;
a := (a + b) / 2;
b := sqrt(b * y);
da := a - b;
end;
result := pi / 2 / a;
end;
// 振り子の角度計算
// L 振り子長さ
// st 時間
// k 離心率
function TForm1.calcQ(L, st, k: double): double;
var
u, Q: double;
begin
result := 0;
if k >= 1 then exit;
u := sqrt(G / L) * st;
Q := k * Jacobi_sn(u, k);
result := arcsin(Q) * 2 / pi * 180;
end;
// Arc 作図
// r 半径
// x,y 原点に対する座標
// st, ed 開始角終了角 deg
// w 線の幅
// c 色
procedure TForm1.drawArc(r, x, y, st, ed:double; w: integer; c: Tcolor);
var
xi, yi : integer;
ri : integer;
xs, ys : integer;
xe, ye : integer;
begin
Image1.Canvas.Pen.Color := c;
Image1.Canvas.Pen.Width := w;
xi := x0 + round(x);
yi := y0 - round(y);
ri := round(r);
xs := round(cos(st / 180 * pi) * r * 2) + xi;
ys := yi - round(sin(st / 180 * pi) * r * 2);
xe := round(cos(ed / 180 * pi) * r * 2) + xi;
ye := yi - round(sin(ed / 180 * pi) * r * 2);
Image1.Canvas.Arc(xi - ri, yi - ri, xi + ri + 1, yi + ri + 1, xs, ys, xe, ye);
end;
// Line 作図
// xs, ys 始点座標
// xe, ye 終点座標
// w 線の幅
// c 線の色
procedure TForm1.drawLine(xs, ys, xe, ye: double; w: integer; c: Tcolor);
var
xsi, ysi : integer;
xei, yei : integer;
begin
Image1.Canvas.Pen.Color := c;
Image1.Canvas.Pen.Width := w;
xsi := x0 + round(xs);
ysi := y0 - round(ys);
xei := x0 + round(xe);
yei := y0 - round(ye);
Image1.Canvas.Pen.Color := c;
Image1.Canvas.Pen.Width := w;
Image1.Canvas.MoveTo(xsi, ysi);
Image1.Canvas.LineTo(xei, yei);
end;
// 角度文字出力
// str 文字
// h 文字の高さ
// Q 文字の角度 deg
procedure TForm1.drawtext(x, y: double; str: string; h: integer; Q: double);
var
xi, yi : integer;
lf, lfold: TLogFont;
begin
xi := x0 + round(x);
yi := y0 - round(y);
//フォントの情報を取得
GetObject(Image1.Canvas.Font.Handle, SizeOf(TLogFont), @lf);
lfold := lf;
lf.lfEscapement := round(Q * 10); // 角度設定
lf.lfHeight := h; // 文字高さ
Image1.Canvas.Font.Handle := CreateFontIndirect(lf);
Image1.Canvas.TextOut(xi, yi, str);
Image1.Canvas.Font.Handle := CreateFontIndirect(lfOld);
end;
// Pendulum作図
// Q 角度 deg
// F true 動画 false 寸法図
procedure TForm1.drawPendulum(Q: double; F: boolean);
var
qr : double; // 角度rad
st, ed : double; // 開始角終了角 deg
L : double; // Pendulum長さ
x, y : double; // Pendulum位置
xs, ys : double; // 直線始点
xe, ye : double; // 直線終点
begin
qr := Q / 180 * pi;
// 支点部半円
L := y0 - y0 / 3;
// 重り円描画
st := 0 + Q ;
ed := 180 + Q;
x := L * sin(qr);
y := - L * cos(qr);
drawArc(50, x, y, ed - 59, st + 59, 2, clBlue);
// 文字出力
if not F then begin
xe := (L - 5) * sin(qr - 0.3);
ye := -(L - 5) * cos(qr - 0.3);
drawtext(xe, ye,'Pendulum', 20, Q);
end
else begin
// 重心位置文字G描画
xe := (L - 20) * sin(qr + 0.07);
ye := -(L - 20) * cos(qr + 0.07);
image1.Canvas.Font.Color := clGreen;
drawtext(xe, ye,'G', 20, Q);
// 支点位置文字o描画
xe := (0 - 23) * sin(qr - 0.25);
ye := -(0 - 23) * cos(qr - 0.25);
image1.Canvas.Font.Color := clRed;
drawtext(xe, ye,'o', 25, Q);
// 支点位置to重心位置Line描画
xs := 5 * sin(qr);;
ys := -5 * cos(qr);
xe := (L - 15) * sin(qr);
ye := -(L - 15) * cos(qr);
drawLine(xs, ys, xe, ye, 1, clFuchsia);
// 重心位置円描画
xs := (L - 10) * sin(qr);
ys := -(L - 10) * cos(qr);
drawArc(4, xs, ys, 0, 360, 2, clBlack);
// 重心迄の距離h描画
xe := L / 2 * sin(qr - 0.1);;
ye := -L / 2 * cos(qr - 0.1);
drawtext(xe, ye,'h', 20, Q);
// 重心位置下矢印描画
ye := ys - 80;
drawLine(xs, ys, xs, ye, 2, clBlack);
xe := xs + 4;
ys := ye + 14;
drawLine(xs, ye, xe, ys, 2, clBlack);
xe := xs - 4;
drawLine(xs, ye, xe, ys, 2, clBlack);
// 質量と加速度文字Mg描画
drawtext(xs - 10, ye,'Mg', 20, 0);
// 角度指示原点線描画
xs := 0;
ys := 0;
xe := 0;
ye := -120;
drawLine(xs, ye, xe, ys, 1, clFuchsia);
// 角度指示円弧描画
if Q > 5 then
drawArc(110, 0, 0, 270, 270 + Q, 1, clFuchsia);
// 角度文字θ描画
xs := (L - 28) * sin(qr - qr / 1.2);
ys := -(L - 28) * cos(qr - qr / 1.2);
drawtext(xs, ys,'θ', 20, Q / 2);
Image1.Canvas.Font.Color := clBlack;
Image1.Canvas.Font.Height := 20;
Image1.Canvas.TextOut(20, 20,'Ig 重心位置Gの慣性モーメント');
Image1.Canvas.TextOut(20, 40,'M 全質量');
Image1.Canvas.TextOut(20, 60,'h 支点Oから重心G迄の距離');
Image1.Canvas.TextOut(20, 80,'θ 振り角度');
Image1.Canvas.TextOut(20, 100,'g 重力加速度 9.80665m/s^2');
end;
// 回転中心描画
drawArc(4, 0, 0, 0, 360, 2, clBlack);
drawArc(25, 0, 0, st, ed, 2, clBlue);
// ロッド部描画
xs := 25 * cos(qr);
ys := 25 * sin(qr);
xe := L * sin(qr) + 50 * cos(qr + 1.05);
ye := -L * cos(qr) - 50 * sin(-qr - 1.05);
drawLine(xs, ys, xe, ye, 2, clBlue);
xs := -25 * cos(qr);
ys := -25 * sin(qr);
xe := L * sin(qr) - 50 * cos(-qr + 1.05);
ye := -L * cos(qr) - 50 * sin(qr - 1.05);
drawLine(xs, ys, xe, ye, 2, clBlue);
end;
// 画像消去
procedure TForm1.ImageClear;
begin
Image1.Canvas.Brush.Style := bsSolid;
Image1.Canvas.Brush.Color := clWhite;
Image1.Canvas.FillRect(Rect(0, 0, Image1.Width, Image1.Height));
end;
// 周期時間 アニメ用角度計算
procedure TForm1.Button1Click(Sender: TObject);
var
h : double; // 支点重心位置距離
M : double; // 質量
Ig : double; // 慣性モーメント
Io : double; // 慣性モーメント
L : double; // 計算用振り子長さ
ch : integer;
k : double; // 離心率
Fk : double; // 第一種完全楕円積分値
w : double;
dt, st : double;
i : integer;
begin
ImageClear;
val(labelededit1.Text, h, ch);
if ch <> 0 then begin
application.MessageBox('支点重心位置距離に間違いがあります。','注意',0);
exit;
end;
if h <= 0 then begin
application.MessageBox('支点重心位置距離がゼロ又はゼロ以下です。','注意',0);
exit;
end;
val(labelededit2.Text, M, ch);
if ch <> 0 then begin
application.MessageBox('質量に間違いがあります。','注意',0);
exit;
end;
if M <= 0 then begin
application.MessageBox('質量がゼロ又はゼロ以下です。','注意',0);
exit;
end;
val(labelededit3.Text, Ig, ch);
if ch <> 0 then begin
application.MessageBox('慣性モーメントに間違いがあります。','注意',0);
exit;
end;
if Ig <= 0 then begin
application.MessageBox('慣性モーメントがゼロ又はゼロ以下です。','注意',0);
exit;
end;
val(labelededit4.Text, Q, ch);
if ch <> 0 then begin
application.MessageBox('振り角度に間違いがあります。','注意',0);
exit;
end;
if Q <= 0 then begin
application.MessageBox('振り角度がゼロ又はゼロ以下です。','注意',0);
exit;
end;
if Q >= 180 then begin
application.MessageBox('振り角度が大きすぎます180°以下にして下さい。','注意',0);
exit;
end;
val(labelededit5.Text, N, ch);
if ch <> 0 then begin
application.MessageBox('アニメ分割数に間違いがあります。','注意',0);
exit;
end;
if N < 10 then begin
application.MessageBox('分割数が10以下です。','注意',0);
exit;
end;
drawPendulum(Q, true); // 振り子作図
k := sin(Q / 180 * pi / 2); // 離心率
Fk := Elip1AGM(k); // 第一種完全楕円積分
Io := Ig + M * h * h; // 回転中心慣性モーメント
L := Io / M / h; // 単振り子長さ相当距離計算
// T := 2 * pi * sqrt(Io / M / G / h); // 微小角周期時間
// T := 4 * sqrt(Io / M / G / h) * Fk; // 周期時間
w := sqrt(L / G); // 周期係数
T := 4 * w * Fk; // 周期時間
memo1.Clear;
memo1.Lines.Add('振り子慣性Io = ' + floatTostrF(Io, ffFixed, 10, 6));
memo1.Lines.Add('単振り子長さ = ' + floatTostrF(L, ffFixed, 10, 6));
memo1.Lines.Add('周期時間 = ' + floatTostrF(T, ffFixed, 10, 6));
setlength(AQ, N + 1); // 角度配列の確保
dt := T / N; // Δt
for i := 0 to N do begin // 配列角度計算
st := i * dt;
AQ[i] := - calcQ(L, st, k);
end;
timer1.Interval := round(dt * 1000); // タイマー設定
if timer1.Interval < 20 then timer1.Interval := 20;
Button2.Enabled := True; // アニメボタンイネーブル
Button2.Caption := 'アニメ開始';
end;
// タイマー割り込み
procedure TForm1.Timer1Timer(Sender: TObject);
begin
if ERF then begin
ERF := False; // 消去フラグクリア
ImageClear; // 画像消去
end;
if TN >= N then TN := 0; // 配列添字クリア
QT := AQ[TN]; // 角度
drawPendulum(Qt, False); // 角度指定描画
ERF := True; // 消去フラグセット
inc(TN); // 配列添字インクリメント
end;
// アニメーション開始停止
procedure TForm1.Button2Click(Sender: TObject);
begin
ImageClear;
ERF := False;
if not Timer1.Enabled then begin
TN := 0;
Button1.Enabled := False;
Timer1.Enabled := True;
Button2.Caption := 'アニメ停止';
end
else begin
Button1.Enabled := true;
Timer1.Enabled := False;
drawPendulum(Q, True);
Button2.Caption := 'アニメ開始';
end;
end;
// 初期設定
procedure TForm1.FormCreate(Sender: TObject);
var
y, z : double;
i : integer;
begin
Timer1.Enabled := False;
Button2.Enabled := False;
X0 := Image1.Width div 2; // 振り子支点座標X
y0 := Image1.Height div 2 - 20; // 振り子支点座標y
memo1.Clear;
drawPendulum(45, true); // 45°作図
// 桁落ち判定値設定
i := 0;
z := 1;
DBL_EPSILON := 1;
repeat
DBL_EPSILON := DBL_EPSILON / 2;
y := z + DBL_EPSILON;
inc(i);
until (y = 1) or (i > 70); // 桁落ちしたら終了
DBL_EPSILON := DBL_EPSILON * 2; // 桁落ち判定値
end;
end.
physical_pendulum.zip