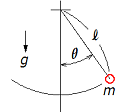
単振り子の周期Ｔは、
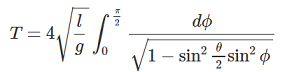で表される計算式となります。計算式の詳細は、インターネットで、単振り子で検索すれば、沢山出てくるのでそちらを参照して下さい。
右の積分式は、第一種完全楕円積分なので簡単に計算することが出来ます。
不完全楕円積分の計算でも、積分範囲を90°にとれば、同じ結果を得ることが出来ますが、第一種完全楕円積分は、１０行程度で答えが得られるので、算術幾何平均でプログラムを組みました。
ランデン変換による積分も、出来る様にしてあります。
単振り子の周期
単振り子の周期Ｔは、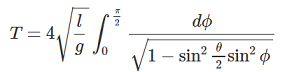で表される計算式となります。
計算式の詳細は、インターネットで、単振り子で検索すれば、沢山出てくるのでそちらを参照して下さい。
右の積分式は、第一種完全楕円積分なので簡単に計算することが出来ます。
不完全楕円積分の計算でも、積分範囲を90°にとれば、同じ結果を得ることが出来ますが、第一種完全楕円積分は、１０行程度で答えが得られるので、算術幾何平均でプログラムを組みました。
ランデン変換による積分も、出来る様にしてあります。
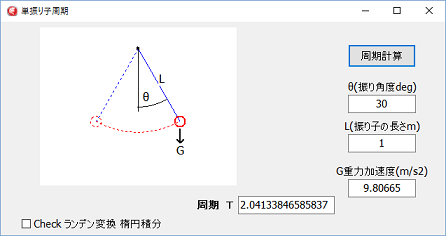
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
Edit1: TEdit;
Label1: TLabel;
Image1: TImage;
CheckBox1: TCheckBox;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
private
{ Private 宣言 }
procedure imageClear;
procedure draw(Q: extended; m : integer);
function Elip1(k: extended): extended;
function Elip1AGM(k: extended): extended;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
// 画像消去
procedure TForm1.imageClear;
begin
with image1.Canvas do begin
Brush.Color := clWhite;
Brush.Style := bsSolid;
FillRect(rect(0, 0, Width, height));
end;
end;
// 作図
procedure TForm1.draw(Q: extended; m : integer);
var
cx, cy : integer;
l, qp : double;
mx, my : integer;
begin
if abs(Q) < 3 then begin
if Q < 0 then Q := -3
else Q := 3;
end;
qp := Q / 180 * pi;
cy := round(abs(Q) / 1.5) + 10;
l := 120;
cx := image1.Width div 2;
mx := round(l * sin(qp)) + cx;
my := round(l * cos(qp)) + cy;
with image1.Canvas do begin
Pen.Color := clblack;
Pen.Width := 2;
Ellipse(cx - 2, cy - 2, cx + 2, cy + 2);
if m = 0 then Pen.Style := pssolid
else Pen.Style := psdot;
Pen.Width := 1;
Pen.Color := clBlue;
MoveTo(cx, cy);
LineTo(mx, my);
if m = 0 then Pen.Width := 2;
Pen.Color := clRed;
arc(mx - 8, my - 8, mx + 8, my + 8,mx - 8, my - 8,mx - 8, my - 8);
if m = 0 then begin
textout((cx + mx) div 2, (cy + my) div 2 - 20, 'L');
textout(mx - 5, my + 30, 'G');
Pen.Color := clblack;
moveto(mx, my + 10);
lineTo(mx, my + 30);
moveto(mx - 5, my + 25);
lineTo(mx, my + 30);
lineTo(mx + 5, my + 25);
end
else
if Q <> 0 then begin
arc(cx - round(l), cy - round(l), cx + round(l) , cy + round(l),
cx + round(l * sin(qp)) , cy + round(l * cos(qp)),
cx + round(l * sin(-qp)) , cy + round(l * cos(-qp)));
pen.Style := psSolid;
pen.color := clBlack;
arc(cx - round(l * 0.7), cy - round(l * 0.7), cx + round(l * 0.7) , cy + round(l * 0.7),
cx, cy + round(l),
cx + round(l * sin(-qp)) , cy + round(l * cos(-qp)));
moveto(cx, cy);
lineTo(cx, cy + round(l * 0.75));
textout(cx + round(l * sin(-qp / 2)) div 2 - 8, cy + round(l * cos(-qp / 2)) div 2, 'θ');
end;
end;
end;
// 第一種完全楕円積分 算術幾何平均
function TForm1.Elip1AGM(k: extended): extended;
var
a, b, y : extended;
da, db : extended;
loop : integer;
begin
a := 1;
b := sqrt(1 - k * k);
da := a - b;
db := 0;
loop := 0;
while da <> db do begin
db := da;
y := a;
a := (a + b) / 2;
b := sqrt(b * y);
da := a - b;
inc(loop);
end;
result := pi / 2 / a;
Form1.Canvas.TextOut(20,250,'積分ループ数 ' + intTostr(loop) + ' ');
end;
// 第一種完全楕円積分 ランデン変換
function TForm1.Elip1(k: extended): extended;
var
t, bt : extended;
loop : integer;
begin
t := 1;
bt := 0;
loop := 0;
while bt <> t do begin
db := da;
bt := t;
k := (1 - sqrt(1 - k * k)) / (1 + sqrt(1 - k * k));
t := t * (1 + K);
inc(loop);
end;
result := pi / 2 * t;
Form1.Canvas.TextOut(20,250,'積分ループ数 ' + intTostr(loop) + ' ');
end;
procedure TForm1.Button1Click(Sender: TObject);
var
C : integer;
Q, L, G : extended;
ek, a , w : extended;
T : extended;
begin
val(LabeledEdit1.Text, Q, c);
if c <> 0 then begin
application.MessageBox('振り角度角度θに間違いがあります。','注意',0);
exit;
end;
if Q > 180 then begin
application.MessageBox('振り角度角度θが大きすぎます。','注意',0);
exit;
end;
if (Q = 180) or (Q = 0) then begin
edit1.Text := '周期無し';
exit;
end;
val(LabeledEdit2.Text, L, c);
if c <> 0 then begin
application.MessageBox('振り子の長さＬに間違いがあります。','注意',0);
exit;
end;
if L <= 0 then begin
application.MessageBox('振り子の長さＬの長さがゼロかマイナスです。','注意',0);
exit;
end;
val(LabeledEdit3.Text, G, c);
if c <> 0 then begin
application.MessageBox('重力加速度Gに間違いがあります。','注意',0);
exit;
end;
if G <= 0 then begin
application.MessageBox('重力加速度がゼロかマイナスです。','注意',0);
exit;
end;
a := sin(Q / 180 * pi / 2);
if checkbox1.Checked then
ek := Elip1(a)
else
ek := Elip1AGM(a);
w := sqrt(G / L);
T := 4 / w * ek;
Edit1.Text := floatTostr(T);
imageClear;
draw( Q, 0);
draw(-Q, 1);
end;
procedure TForm1.FormCreate(Sender: TObject);
var
Bitmap: Tbitmap;
begin
Caption := '単振り子周期';
Bitmap := TBitmap.Create;
Bitmap.Width := Image1.Width;
Bitmap.height:= Image1.height;
with Image1 do begin
Picture.Graphic := Bitmap;
Canvas.Font.Height := 15;
end;
Bitmap.Free;
image1.Canvas.Font.Size := 13;
draw( 30, 0);
draw(-30, 1);
end;
end.
pendulum.zip