2023/06/12
n次多項式補間のプログラムにバグが有ったので、修正しました。
ニュートン補間、ラグランジュ補間
ニュートン補間についてはウィキペディアのニュートン補間 ラグランジュ補間についての詳細はウィキペディアのラグランジュ補間 をそれぞれ参照して下さい。
補間となっていますが、計算はデーターの数をNとすると n=N-1 のn次方程式の計算による場合と同じになります。
n次方程式の場合、近似計算のn次回帰計算をする必要がありますが、ニュートン、ラグランジュ補間は、単純な計算で行うことが出来ます。
計算上の注意点は、関数の逆数を含まないデーターでないと発散(.ルンゲ現象)する場合がある事、同じ X の値が有ってはならない事です。
Xの値は等間隔である必用はありません。
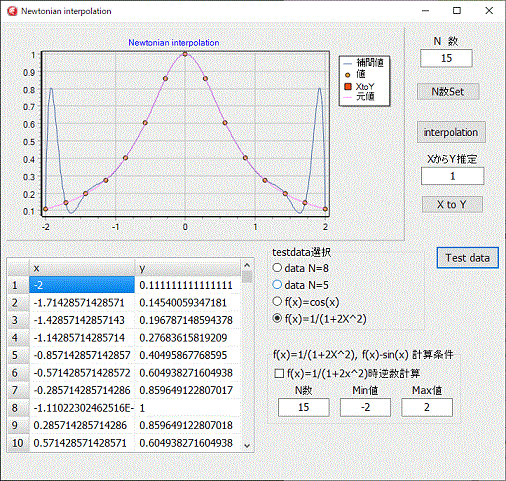左図はルンゲ現象が発生している例です。
テストデーターの計算にf(x)=1/(1+2x^2)を使用した場合で、逆数になっているので、ルンゲ現象が発生します。
f(x)=cos(x)や対数をテストデーターに使用しても発生しません。
当然1～N-1次の計算をテストデーターに使用すれば発生はしません。
f(x)=1/(2 + cos(x))のような関数だとcos(x)でもルンゲ現象は発生します。
プログラムに、
f(x)=1/(1+2x^2)の時逆数計算の指定があるのは、1/f(x)=1+2x^2で計算すればルンゲ現象が発生しない事を確認するためのものです。
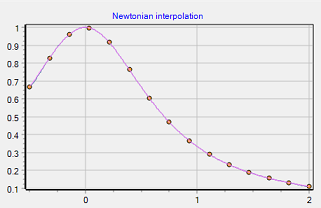左図はf(x)=1/(1+2x^2)のxの範囲を0.5～2にした場合ですが、ルンゲ現象は小さな値に抑えられ伸す。
xの範囲を0～2にすると、ルンゲ現象は発生しなくなります。
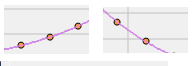凸カーブデーターの左右に、凹む様に変化する部分があり、そのカーブが、関数の逆数になっている場合です。
片方だけだと、ルンゲ現象は発生しません。
実際のデーターは何らかの測定データー、サンプリングデーターであり、計算値の様に揃う事は無いので、関数の逆数になってしまう部分が発生すると思われ、ニュートン補間、ラグランジュ補間を使用する場合は、必ず補間グラフを作成して、問題が無いか確認する必要があります。
又、N数を増やしすぎると、:計算の最大次数がN-1となり、桁落ちの発生が起きるので注意が必要です。
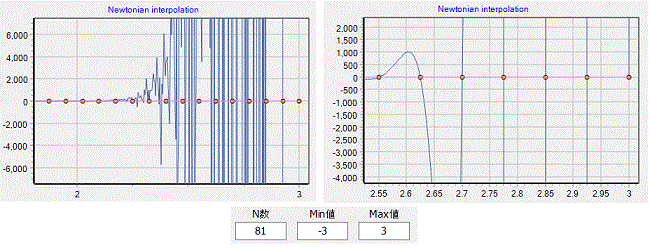N数を余り増やすと、桁落ちが発生して、左図左側の様に、発振したようになりのす。
桁落ちしているかどうかは、グラフのN点を補間値が通らなくなるのと、ギザギザになることで見分けます。
左図右側は、多倍長演算で、桁落ちしていない場合です。
プログラム
ニュートン補間
// データー数(N) - 1 の n次回帰計算と同じ結果になります。 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, Vcl.StdCtrls, VCLTee.TeEngine, VCLTee.Series, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart, Vcl.Grids; type TForm1 = class(TForm) Chart1: TChart; Series1: TLineSeries; Series3: TPointSeries; StringGrid1: TStringGrid; NEdit: TLabeledEdit; NsetBtn: TButton; interpolationBtn: TButton; Series2: TPointSeries; XEdit: TLabeledEdit; XtoYBtn: TButton; Series4: TLineSeries; GroupBox1: TGroupBox; testNEdit: TLabeledEdit; CheckBox2: TCheckBox; MinXEdit: TLabeledEdit; MaxXEdit: TLabeledEdit; RadioGroup1: TRadioGroup; testdataBtn: TButton; procedure testdataBtnClick(Sender: TObject); procedure NsetBtnClick(Sender: TObject); procedure interpolationBtnClick(Sender: TObject); procedure FormCreate(Sender: TObject); procedure XtoYBtnClick(Sender: TObject); private { Private 宣言 } procedure GridSet(Sin, Colin: integer); procedure FGridSet(Sin, Colin: integer); // グリッドサイズ変更 public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses system.Math; type DArray = array of double; var x, ncd : Darray; P : integer; dx, xmax, xmin : double; FF : boolean; // グリッドサイズの変更 procedure TForm1.GridSet(Sin, Colin: integer); // グリッドサイズ変更 var // データー行の数は10迄 H, W:integer; // それ以上はスクロールする begin if (StringGrid1.ColCount = Colin) and (StringGrid1.RowCount = Sin) then exit; StringGrid1.ColWidths[0] := 30; StringGrid1.ColCount := Colin; StringGrid1.RowCount := Sin; if Sin <= 11 then // ストリンググリッドの大きさ設定 begin // 固定行を含め11行又はそれ以下の場合 H := (StringGrid1.DefaultRowHeight + 1) * Sin; W := (StringGrid1.DefaultColWidth + 1) * (Colin - 1) + 31; StringGrid1.ScrollBars := ssNone; // スクロールバーなし end else begin // 固定行を含め11行より多い場合 H := (StringGrid1.DefaultRowHeight + 1) * (10 + 1); W := (StringGrid1.DefaultColWidth + 1) * (Colin - 1) + 31; StringGrid1.ScrollBars := ssVertical; // スクロールバー表示 end; StringGrid1.ClientWidth := W; StringGrid1.ClientHeight := H; end; // グリッド固定行の設定 procedure TForm1.FGridSet(Sin, Colin: integer); var E : integer; begin GridSet(Sin, Colin); for E := 1 to Sin - 1 do StringGrid1.Rows[E].Text := intTostr(E); StringGrid1.Cols[1].Text := 'x'; StringGrid1.Cols[2].Text := 'y'; end; // N数入力 入力ミス N < 0 function Ninput(testF: boolean): integer; var N, ch : integer; begin result := -1; if not testF then val(Form1.Nedit.Text, N, ch) else val(Form1.testNedit.Text, N, ch); if ch <> 0 then begin application.MessageBox('N数の入力に間違いが有ります。','注意',0); exit; end; if N > 100 then begin application.MessageBox('N数は100迄にして下さい。','注意',0); exit; end; if N < 3 then begin application.MessageBox('N数は3以上にして下さい。','注意',0); exit; end; result := N; end; // グリッドN数セット procedure TForm1.NsetBtnClick(Sender: TObject); var N : integer; begin N := Ninput(false); if N < 0 then exit; GridSet(N + 1, 3); end; // 参考値f(x) ルンゲ現象確認用データー function f(x: double): double; begin result := 1 / (1 + 2 * x * x); end; // 参考値cos(x) function f1(x: double): double; begin result := cos(x); end; // 参考値 セット procedure TForm1.testdataBtnClick(Sender: TObject); var N : integer; i, ch : integer; x, y : Darray; minx, maxx :double; p, xd, yd : double; begin N := 8; // データー数 FF := False; Series1.Clear; Series3.Clear; if radiogroup1.ItemIndex = 0 then begin N := 8; // データー数 Nedit.Text := inttostr(N); GridSet(N + 1, 3); setlength(x, N); setlength(y, N); x[0] := -8; y[0] := 2; x[1] := -5; y[1] := 3; x[2] := -3; y[2] := 1; x[3] := 0; y[3] := 2; x[4] := 2; y[4] := 1; x[5] := 5; y[5] := 3; x[6] := 8; y[6] := -4; x[7] := 9; y[7] := 1; end; if radiogroup1.ItemIndex = 1 then begin N := 5; Nedit.Text := inttostr(N); GridSet(N + 1, 3); setlength(x, N); setlength(y, N); x[0] := 0; y[0] := 0.8; x[1] := 2; y[1] := 3.4; x[2] := 3; y[2] := 4.9; x[3] := 4; y[3] := 2.9; x[4] := 5; y[4] := 2; end; if (radiogroup1.ItemIndex = 0) or (radiogroup1.ItemIndex = 1) then begin for i := 0 to N - 1 do begin StringGrid1.cells[1,i + 1] := floatTostr(x[i]); StringGrid1.cells[2,i + 1] := floatTostr(y[i]) end; end; if (radiogroup1.ItemIndex = 2) or (radiogroup1.ItemIndex = 3) then begin N := Ninput(true); if N < 0 then exit; val(MinXedit.Text, minx, ch); if ch <> 0 then begin application.MessageBox('min値に間違いが有ります。','注意',0); exit; end; val(MaxXedit.Text, maxx, ch); if ch <> 0 then begin application.MessageBox('max値に間違いが有ります。','注意',0); exit; end; if minx >= maxx then begin application.MessageBox('max値がmin値より小さな値になっています。','注意',0); exit; end; Nedit.Text := inttostr(N); GridSet(N + 1, 3); p := (maxx - minx) / (N - 1); for i := 0 to N - 1 do begin xd := i * p + minx; yd := 0; case radiogroup1.ItemIndex of 2 : yd := f1(xd); 3 : yd := f(xd); end; StringGrid1.cells[1,i + 1] := floatTostr(xd); StringGrid1.cells[2,i + 1] := floatTostr(yd); end; if (Form1.CheckBox2.Checked = true) and (radiogroup1.ItemIndex = 3) then FF := True; end; interpolationBtnClick(nil); end; // 係数テーブル設定 function maketable(var x, ncd: DArray; P: integer): Boolean; // 係数を求めncdに上書き var i, j : integer; begin result := False; for j := 0 to P do for i := 0 to P do begin if j <> i then if x[i] = x[j] then begin application.MessageBox(pchar('x' + inttostr(j+1) + ' x' + inttostr(i+1) + 'が同じ値です。'),'注意',0); exit; end; end; for i := 1 to P do for j := P downto i do ncd[j] := (ncd[j] - ncd[j - 1]) / (x[j] - x[j - i]); result := True; end; // 補間計算 function interpolate(x, ncd: DArray; P: integer; xx: double): double; // 補間 var i : integer; r, s : double; begin r := ncd[0]; s := 1; for i := 1 to P do begin s := s * (xx - x[i - 1]); r := r + s * ncd[i]; end; // こちらの計算でもOk { r := ncd[P]; for i := P - 1 downto 0 do r := r * (xx - x[i]) + ncd[i]; } if not FF then result := r else if r = 0 then result := 1 else result := 1 / r; end; // グリッドの値による補間計算 procedure TForm1.interpolationBtnClick(Sender: TObject); var N, ch, i, imax : integer; y : Darray; cn : string; s, xx : double; begin XtoYBtn.Enabled := False; N := Ninput(false); if N < 0 then exit; GridSet(N + 1, 3); setlength(x, N); setlength(y, N); setlength(ncd, N); for i := 0 to N - 1 do begin val(StringGrid1.cells[1,i + 1], x[i], ch); if ch <> 0 then begin cn := 'x' + intTostr(i + 1) + 'に間違いが有ります。'; application.MessageBox(pchar(cn),'注意',0); break; end; val(StringGrid1.cells[2,i + 1], y[i], ch); if ch <> 0 then begin cn := 'y' + intTostr(i + 1) + 'に間違いが有ります。'; application.MessageBox(pchar(cn),'注意',0); break; end; if not FF then ncd[i] := y[i] else ncd[i] := 1 / y[i]; end; if ch <> 0 then exit; Series1.Clear; Series2.Clear; Series3.Clear; Series4.Clear; P := N - 1; if not maketable(x, ncd, P) then exit; // テーブルの作成 xmax := x[0]; xmin := x[0]; for i := 0 to P do begin if x[i] > xmax then xmax := x[i]; if x[i] < xmin then xmin := x[i]; Series3.AddXY(x[i], y[i]); end; imax := P * 20; dx := (xmax - xmin) / imax; for i := 0 to imax do begin xx := i * dx + x[0]; if radiogroup1.ItemIndex = 2 then begin s := f1(xx); // 元値計算 Series4.AddXY(xx, s); end; if radiogroup1.ItemIndex = 3 then begin s := f(xx); // 元値計算 Series4.AddXY(xx, s); end; s := interpolate(x, ncd, P, xx); // 補間計算 Series1.AddXY(xx, s) end; XtoYBtn.Enabled := True; end; // 指定値計算 指定値xによるy補間値計算とグラフ表示 procedure TForm1.XtoYBtnClick(Sender: TObject); var i, j, ch : integer; xd, xx, s, gmin, gmax : double; begin val(Xedit.Text, xd, ch); if ch <> 0 then begin application.MessageBox('xからy推定の入力に間違いが有ります。','注意',0); exit; end; // gmin-gmax範囲グラフ再描画 Series1.Clear; gmin := xmin; gmax := xmax; if xd < xmin then gmin := xd; if xd > xmax then gmax := xd; i := round((gmax - gmin) / dx); for j := 0 to i do begin xx := j * dx + gmin; s := interpolate(x, ncd, P, xx); // 補間計算 Series1.AddXY(xx, s); end; // 指定値xによるy補間値計算とグラフ表示 Series2.Clear; s := interpolate(x, ncd, P, xd); // 補間計算 Series2.AddXY(xd, s); end; // グリッド初期設定 procedure TForm1.FormCreate(Sender: TObject); begin FGridSet(101, 3); // 固定行1列1 + 100行2列まで行列を変更しても // 入力値がクリアされないようにします。 GridSet(4, 3); // 最初の設定 end; end.
ラグランジェ補間
係数テーブルを作成せず補間値をX,Yの配列値からその都度計算します。
計算結果はニュートン補間と同じで、N-1次計算による補間値となります。
計算式は、非常に簡単なものとなります。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, Vcl.StdCtrls,
VCLTee.TeEngine, VCLTee.Series, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart,
Vcl.Grids;
type
TForm1 = class(TForm)
Chart1: TChart;
Series1: TLineSeries;
Series3: TPointSeries;
StringGrid1: TStringGrid;
NEdit: TLabeledEdit;
NsetBtn: TButton;
interpolationBtn: TButton;
testdataBtn: TButton;
Series2: TPointSeries;
XEdit: TLabeledEdit;
XtoYBtn: TButton;
Series4: TLineSeries;
GroupBox1: TGroupBox;
CheckBox2: TCheckBox;
TestNEdit: TLabeledEdit;
MinXEdit: TLabeledEdit;
MaxXEdit: TLabeledEdit;
RadioGroup1: TRadioGroup;
procedure testdataBtnClick(Sender: TObject);
procedure NsetBtnClick(Sender: TObject);
procedure interpolationBtnClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure XtoYBtnClick(Sender: TObject);
private
{ Private 宣言 }
procedure GridSet(Sin, Colin: integer);
procedure FGridSet(Sin, Colin: integer); // グリッドサイズ変更
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses system.Math;
type
DArray = array of double;
var
x, y, yd : Darray;
N : integer;
dx, xmax, xmin : double;
FF : boolean;
// グリッドサイズの変更
procedure TForm1.GridSet(Sin, Colin: integer); // グリッドサイズ変更
var // データー行の数は10迄
H, W :integer; // それ以上はスクロールする
begin
if (StringGrid1.ColCount = Colin) and (StringGrid1.RowCount = Sin) then exit;
StringGrid1.ColWidths[0] := 30;
StringGrid1.ColCount := Colin;
StringGrid1.RowCount := Sin;
if Sin <= 11 then // ストリンググリッドの大きさ設定
begin // 固定行を含め11行又はそれ以下の場合
H := (StringGrid1.DefaultRowHeight + 1) * Sin;
W := (StringGrid1.DefaultColWidth + 1) * (Colin - 1) + 31;
StringGrid1.ScrollBars := ssNone; // スクロールバーなし
end
else
begin // 固定行を含め11行より多い場合
H := (StringGrid1.DefaultRowHeight + 1) * (10 + 1);
W := (StringGrid1.DefaultColWidth + 1) * (Colin - 1) + 31;
StringGrid1.ScrollBars := ssVertical; // スクロールバー表示
end;
StringGrid1.ClientWidth := W;
StringGrid1.ClientHeight := H;
end;
// グリッド固定行の設定
procedure TForm1.FGridSet(Sin, Colin: integer);
var
E : integer;
begin
GridSet(Sin, Colin);
for E := 1 to Sin - 1 do
StringGrid1.Rows[E].Text := intTostr(E);
StringGrid1.Cols[1].Text := 'x';
StringGrid1.Cols[2].Text := 'y';
end;
// N数入力 エラー時戻り値<0
function Ninput(testF: boolean): integer;
var
N, ch: integer;
begin
result := -1;
if not testF then
val(Form1.Nedit.Text, N, ch)
else
val(Form1.testNedit.Text, N, ch);
if ch <> 0 then begin
application.MessageBox('N数の入力に間違いが有ります。','注意',0);
exit;
end;
if N > 100 then begin
application.MessageBox('N数は100迄にして下さい。','注意',0);
exit;
end;
if N < 3 then begin
application.MessageBox('N数は3以上にして下さい。','注意',0);
exit;
end;
result := N;
end;
// グリッドN数セット
procedure TForm1.NsetBtnClick(Sender: TObject);
var
N : integer;
begin
N := Ninput(false);
if N < 0 then exit;
GridSet(N + 1, 3);
end;
// xの値チェック 同じxの値があるか確認 同じ値無 true 有り false
function datacheck(x :DArray): boolean;
var
i, j : integer;
begin
result := True;
for i := Low(x) to High(x) do
for j := Low(x) to High(x) do begin
if i <> j then
if x[i] - x[j] = 0 then begin
application.MessageBox(pchar('Ｘ' + inttostr(i+1) + ' Ｘ' + inttostr(j+1)
+ 'が同じ値です。'),'注意',0);
result := False;
exit;
end;
end;
end;
// 補間計算
function interpolate(x, y: DArray; xx: double): double;
var
i, j : integer;
s, p : double;
begin
s := 0;
for i := Low(x) to High(x) do begin
p := y[i];
for j := Low(x) to High(x) do begin
if i <> j then
p := p * (xx - x[j]) / (x[i] - x[j]);
end;
s := s + p;
end;
result := s;
end;
// 参考値f(x) ルンゲ現象確認用データー
function f(x: double): double;
begin
// x := abs(x);
result := 1 / (1 + 2 * x * x);
end;
// 参考値 セット
procedure TForm1.testdataBtnClick(Sender: TObject);
var
N, ch : integer;
i : integer;
p, minx, maxx :double;
x, y : Darray;
xd, yd : double;
begin
Series1.Clear;
Series3.Clear;
FF := False;;
N := 5;
if radiogroup1.ItemIndex = 0 then begin
N := 8; // データー数
Nedit.Text := inttostr(N);
GridSet(N + 1, 3);
setlength(x, N);
setlength(y, N);
x[0] := -8; y[0] := 2;
x[1] := -5; y[1] := 3;
x[2] := -3; y[2] := 1;
x[3] := 0; y[3] := 2;
x[4] := 2; y[4] := 1;
x[5] := 5; y[5] := 3;
x[6] := 8; y[6] := -4;
x[7] := 9; y[7] := 1;
end;
if radiogroup1.ItemIndex = 1 then begin
N := 5; // データー数
Nedit.Text := inttostr(N);
GridSet(N + 1, 3);
setlength(x, N);
setlength(y, N);
x[0] := 0; y[0] := 0.8;
x[1] := 2; y[1] := 3.4;
x[2] := 3; y[2] := 4.9;
x[3] := 4; y[3] := 2.9;
x[4] := 5; y[4] := 2;
end;
if (radiogroup1.ItemIndex = 0) or (radiogroup1.ItemIndex = 1) then
for i := 0 to N - 1 do begin
StringGrid1.cells[1,i + 1] := floatTostr(x[i]);
StringGrid1.cells[2,i + 1] := floatTostr(y[i]);
end;
if radiogroup1.ItemIndex = 2 then begin
N := Ninput(true);
if N < 0 then exit;
val(minxedit.Text, minx, ch);
if ch <> 0 then begin
application.MessageBox('Min値に間違いが有ります。','注意',0);
exit;
end;
val(maxxedit.Text, maxx, ch);
if ch <> 0 then begin
application.MessageBox('Max値に間違いが有ります。','注意',0);
exit;
end;
if minx >= maxx then begin
application.MessageBox('Max値がMin値より小さいです。','注意',0);
exit;
end;
Nedit.Text := inttostr(N);
GridSet(N + 1, 3);
p := (maxx - minx) / (N - 1);
for i := 0 to N - 1 do begin
xd := i * p + minx;
yd := f(xd);
StringGrid1.cells[1,i + 1] := floatTostr(xd);
StringGrid1.cells[2,i + 1] := floatTostr(yd);
end;
if checkbox2.Checked = True then FF := true;
end;
interpolationBtnClick(Nil);
end;
// グリッドの値による補間計算
procedure TForm1.interpolationBtnClick(Sender: TObject);
var
ch, i, imax : integer;
cn : string;
s, xx : double;
begin
XtoYBtn.Enabled := False;
N := Ninput(false);
if N < 0 then exit;
GridSet(N + 1, 3);
setlength(x, N);
setlength(y, N);
setlength(yd, N);
for i := 0 to N - 1 do begin
val(StringGrid1.cells[1,i + 1], x[i], ch);
if ch <> 0 then begin
cn := 'x' + intTostr(i + 1) + 'に間違いが有ります。';
application.MessageBox(pchar(cn),'注意',0);
break;
end;
val(StringGrid1.cells[2,i + 1], y[i], ch);
if ch <> 0 then begin
cn := 'y' + intTostr(i + 1) + 'に間違いが有ります。';
application.MessageBox(pchar(cn),'注意',0);
break;
end;
end;
if ch <> 0 then exit;
if not datacheck(x) then exit; // xの値に重複が無いか確認
Series1.Clear;
Series2.Clear;
Series3.Clear;
Series4.Clear;
xmin := x[0];
xmax := x[0];
for i := 0 to N - 1 do begin
if x[i] > xmax then xmax := x[i];
if x[i] < xmin then xmin := x[i];
Series3.AddXY(x[i], y[i]);
if FF then yd[i] := 1 / y[i]
else yd[i] := y[i];
end;
imax := (N - 1) * 20; // 分割数
dx := (xmax - xmin) / imax;
for i := 0 to imax do begin
xx := i * dx + x[0];
if radiogroup1.ItemIndex = 2 then begin
s := f(xx);
Series4.AddXY(xx, s);
end;
s := interpolate(x, yd, xx); // 補間計算
if FF then s := 1 / s;
Series1.AddXY(xx, s);
end;
XtoYBtn.Enabled := True;
end;
// 指定値グラフ表示 指定値xによるy補間値計算とグラフ表示
procedure TForm1.XtoYBtnClick(Sender: TObject);
var
i, j, ch : integer;
xd, s, xx, gmin, gmax : double;
begin
val(Xedit.Text, xd, ch);
if ch <> 0 then begin
application.MessageBox('xからY推定の入力に間違いが有ります。','注意',0);
exit;
end;
// 最小最大区間グラフ再描画
Series1.Clear;
gmin := xmin;
gmax := xmax;
if xd < xmin then gmin := xd;
if xd > xmax then gmax := xd;
i := round((gmax - gmin) / dx);
for j := 0 to i do begin
xx := j * dx + gmin;
s := interpolate(x, yd, xx); // 補間計算
if FF then s := 1 / s;
Series1.AddXY(xx, s);
end;
// 指定値xによるy補間値計算とグラフ表示
Series2.Clear;
s := interpolate(x, yd, xd); // 補間計算
if FF then s := 1 / s;
Series2.AddXY(xd, s);
end;
// グリッド初期設定
procedure TForm1.FormCreate(Sender: TObject);
begin
FGridSet(101, 3); // 固定行1列1 + 100行2列まで行列を変更しても
// 入力値がクリアされないようにします。
GridSet(4, 3); // 最初の設定
end;
end.
ｎ次回帰近似による補間
ニュートン補間の計算確認の為、ｎ次回帰計算のｎの値をN-1として、n次回帰近似(polynomial
approximation)プログラムを作成してみました。
次数がN-1の時は、ニュートン補間と同じ結果になります、次数をN-1より小さい値に設定ると、n次回帰近似計算となります。
次数がN-1の時は、回帰曲線が必ずデーター点を通ります、その時のデーターに同じx値が有ってはなりません。
データー点を必ず通る必要がない場合は、回帰計算の次数を0～N-1の値に出来ます。
同じx値の値が複数あっても、問題なく計算が出来ます。
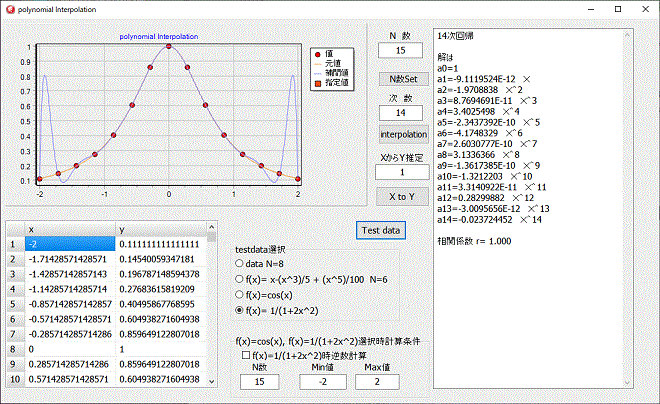計算結果は、ニュートン補間、ラグランジュ補間と変わりません。
N数増加による桁落ちはニュートン補間、ラグランジュ補間より少なくなります。
計算次数は、testdataの時はN-1になりますが、その後補間(interpolation)計算では0～N-1の間で自由に指定が出来ます。
unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, Vcl.StdCtrls, VCLTee.TeEngine, VCLTee.Series, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart, Vcl.Grids; type TAoAoD = array of array of extended; // 引数で渡す多次元配列はここでtype宣言 Darray = array of extended; TForm1 = class(TForm) Chart1: TChart; StringGrid1: TStringGrid; NEdit: TLabeledEdit; NsetBtn: TButton; interpolationBtn: TButton; testdataBtn: TButton; XEdit: TLabeledEdit; Series1: TPointSeries; Series2: TLineSeries; Series3: TLineSeries; Series5: TPointSeries; Xin_interpolation: TButton; Memo1: TMemo; RadioGroup1: TRadioGroup; GroupBox1: TGroupBox; CheckBox2: TCheckBox; MinXEdit: TLabeledEdit; MaxXEdit: TLabeledEdit; TestNEdit: TLabeledEdit; ZEdit: TLabeledEdit; procedure testdataBtnClick(Sender: TObject); procedure NsetBtnClick(Sender: TObject); procedure interpolationBtnClick(Sender: TObject); procedure FormCreate(Sender: TObject); procedure Xin_interpolationClick(Sender: TObject); procedure CheckBox2Click(Sender: TObject); private { Private 宣言 } procedure GridSet(Sin, Colin: integer); procedure FGridSet(Sin, Colin: integer); // グリッドサイズ変更 procedure gauss(ad: TAoAoD; xxd: DArray; N : integer); procedure sai(xi, yi, xxd: DArray; N, S : integer); // n次計算ルーチン public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses system.Math; var x, y, xx : Darray; DEF, DEFD: Boolean; xmax, xmin, dx : extended; // グリッドサイズの変更 procedure TForm1.GridSet(Sin, Colin: integer); // グリッドサイズ変更 var // データー行の数は10迄 H, W :integer; // それ以上はスクロールする begin if (StringGrid1.ColCount = Colin) and (StringGrid1.RowCount = Sin) then exit; StringGrid1.ColWidths[0] := 30; StringGrid1.ColCount := Colin; StringGrid1.RowCount := Sin; if Sin <= 11 then // ストリンググリッドの大きさ設定 begin // 固定行を含め11行又はそれ以下の場合 H := (StringGrid1.DefaultRowHeight + 1) * Sin; W := (StringGrid1.DefaultColWidth + 1) * (Colin - 1) + 31; StringGrid1.ScrollBars := ssNone; // スクロールバーなし end else begin // 固定行を含め11行より多い場合 H := (StringGrid1.DefaultRowHeight + 1) * (10 + 1); W := (StringGrid1.DefaultColWidth + 1) * (Colin - 1) + 31; StringGrid1.ScrollBars := ssVertical; // スクロールバー表示 end; StringGrid1.ClientWidth := W; StringGrid1.ClientHeight := H; end; // グリッド固定行の設定 procedure TForm1.FGridSet(Sin, Colin: integer); var E : integer; begin GridSet(Sin, Colin); for E := 1 to Sin - 1 do StringGrid1.Rows[E].Text := intTostr(E); StringGrid1.Cols[1].Text := 'x'; StringGrid1.Cols[2].Text := 'y'; end; // N数入力 入力エラー result < 0 function Ninput(testF : boolean; var Z: integer): integer; var N, ch : integer; begin result := -1; if not testF then val(Form1.Nedit.Text, N, ch) else val(Form1.testNedit.Text, N, ch); if ch <> 0 then begin application.MessageBox('N数の入力に間違いが有ります。','注意',0); exit; end; if (N < 3) or (N > 100) then begin application.MessageBox('N数は3～100にして下さい。','注意',0); exit; end; val(Form1.Zedit.Text, Z, ch); if ch <> 0 then begin application.MessageBox('次数Zの入力に間違いが有ります。','注意',0); exit; end; if Z > N - 1 then begin application.MessageBox('次数ZがN数より大きいので小さくします。','注意',0); Z := N - 1; Form1.Zedit.Text := intTostr(Z); end; if Z < 0 then begin application.MessageBox('次数はゼロ以上にしてください。','注意',0); exit; end; result := N; end; // グリッドN数セット procedure TForm1.NsetBtnClick(Sender: TObject); var N, Z : integer; begin N := Ninput(false, Z); if N < 0 then exit; GridSet(N + 1, 3); end; // xの値チェック 同じxの値があるか確認 同じ値無 true 有り false function datacheck(x :DArray; N: integer): boolean; var i, j : integer; begin result := true; for i := 0 to N - 1 do for j := 0 to N - 1 do begin if i <> j then if x[i] - x[j] = 0 then begin application.MessageBox(pchar('x' + inttostr(i+1) + '-x' + inttostr(j+1) + 'がゼロになります。'),'注意',0); result := false; exit; end; end; end; // 参考値f(x) ルンゲ現象確認用データー function f3(x: extended): extended; begin result := cos(x); end; // 参考値f(x) ルンゲ現象確認用データー function f2(x: extended): extended; begin // x := abs(x); result := 1 / (1 + 2 * x * x); end; // 参考値の関数 function f(x: extended): extended; begin result := x - power(x,3) / 5 + power(x,5) / 100; end; // 参考値 セット procedure TForm1.testdataBtnClick(Sender: TObject); var N, Z : integer; i, ch : integer; d, pc : extended; minx, maxx : extended; xd, yd : extended; begin DEFD := False; N := 5; if radiogroup1.ItemIndex = 0 then begin N := 8; // データー数 Nedit.Text := inttostr(N); Zedit.Text := inttostr(N - 1); GridSet(N + 1, 3); setlength(x, N); setlength(y, N); x[0] := -8; y[0] := 2; x[1] := -5; y[1] := 3; x[2] := -3; y[2] := 1; x[3] := 0; y[3] := 2; x[4] := 2; y[4] := 1; x[5] := 5; y[5] := 3; x[6] := 8; y[6] := -4; x[7] := 9; y[7] := 1; DEF := False; // 差分グラフ表示フラグ end; if radiogroup1.ItemIndex = 1 then begin N := 6; Nedit.Text := inttostr(N); Zedit.Text := inttostr(N - 1); GridSet(N + 1, 3); setlength(x, N); setlength(y, N); minx := - 4.5; maxx := 4.5; pc := (maxx - minx) / (N - 1); for i := 0 to N - 1 do begin d := i * Pc + minx; x[i] := d; y[i] := f(d); end; DEF := True; // 差分グラフ表示フラグ end; if (radiogroup1.ItemIndex = 0) or (radiogroup1.ItemIndex = 1) then begin for i := 0 to N - 1 do begin StringGrid1.cells[1,i + 1] := floatTostr(x[i]); StringGrid1.cells[2,i + 1] := floatTostr(y[i]); end; end; if (radiogroup1.ItemIndex = 2) or (radiogroup1.ItemIndex = 3) then begin N := Ninput(true, Z); Zedit.Text := inttostr(N - 1); if N < 0 then begin exit; end; val(MinXedit.Text, minx, ch); if ch <> 0 then begin application.MessageBox('Min値の入力に間違いが有ります。','注意',0); exit; end; val(MaxXedit.Text, maxx, ch); if ch <> 0 then begin application.MessageBox('Max値の入力に間違いが有ります。','注意',0); exit; end; if minx >= maxx then begin application.MessageBox('Max値がMax値より大きくなっています。','注意',0); exit; end; Nedit.Text := inttostr(N); GridSet(N + 1, 3); pc := (maxx - minx) / (N - 1); yd := 0; for i := 0 to N - 1 do begin xd := i * pc + minx; case radiogroup1.ItemIndex of 2: yd := f3(xd); 3: begin yd := f2(xd); if checkbox2.Checked = True then DEFD := True; end; end; StringGrid1.cells[1,i + 1] := floatTostr(xd); StringGrid1.cells[2,i + 1] := floatTostr(yd); end; DEF := True; // 差分グラフ表示フラグ end; interpolationBtnClick(Nil); end; // ガウスの消去法ルーチン procedure TForm1.gauss(ad: TAoAoD; xxd: DArray; N : integer); var i, j, k, pivot: integer; b : extended; p, q, max: extended; LL : string; begin // N := High(xxd) + 1; // 配列a[i,k]をkで スキャン for K := 0 to N -1 do // 配列a[i,k]をk スキャン begin max := 0; // Max値初期化 pivot := K; // ピボット仮設定 for i := K to N -1 do // 配列a[i,k]をi 縦スキャン begin if abs(ad[i, k]) > max then // k列の中で一番大きい値を選ぶ begin max := abs(ad[i, k]); pivot := i; // ピボットに設定 end; end; // pivotがkと違えば、pivotとkの行の入れ替え if pivot <> k then for j := 0 to N do // 横方向にjでスキャンしてa[k, j]とa[pivot,j]をいれかえ begin b := ad[k, j]; ad[k, j] := ad[pivot, j]; ad[pivot, j] := b; end; // a[k,k] が１になるように、横方向にjでスキャン p := ad[k, k]; // 対角要素を保存 ad[k, k] := 1; // １になる事がわかっているのでa[k, K +1]から計算 for j := k + 1 to N do ad[K, j] := ad[K, j] / p; // a[i,k] を、縦方向にスキャン for i := 0 to N - 1 do begin if k <> i then // 対角要素は1になっているので計算しない begin q := ad[i, k]; // a[i,k] が0 になるように横方向にスキャン ad[i, k] := 0; // ゼロになる事がわかっているのでa[i,K + 1]から計算 for j := k + 1 to N do ad[i, j] := ad[i, j] - q * ad[k, j]; end; end; end; // 戻り値の設定 for i := 0 to N - 1 do xxd[i] := ad[i, N]; Memo1.Clear; LL := intTostr(N - 1) + '次回帰'; Memo1.Lines.Add(LL); { LL := '配列結果表示'; Memo1.Lines.Add(LL); // 行列の最後がどうなったか見たいとき実行 for i := 0 to N - 1 do begin LL := ''; for j := 0 to N do LL := LL + floatTostrF(a[i, j], ffGeneral, 7, 5) + ' '; Memo1.Lines.Add(LL); end; } Memo1.Lines.Add(''); LL := '解は'; Memo1.Lines.Add(LL); for i := 0 to N - 1 do begin LL := floatTostrF(xx[i],ffGeneral, 8, 5); if i = 0 then LL :='a0=' + LL; if i = 1 then LL :='a1=' + LL + ' Ｘ'; if i > 1 then LL :='a' + intTostr(i) + '=' + LL + ' Ｘ＾' + intTostr(i); Memo1.Lines.Add(LL); end; end; // n次回帰計算用データーの配列割付と、ガウスサブルーチンの呼び出し procedure TForm1.sai(xi, yi, xxd: DArray; N, S : integer); // n次計算ルーチン var i, j, k: integer; a: TAoAoD; yha, yj: DArray; my: extended; Sy,Syh, r: extended; LL : string; begin // N := high(xxd) + 1; // S := high(xi) + 1; SetLength(a, N, N + 1); // ガウス計算用配列確保 SetLength(YhA, S); // 推定値用配列確保 SetLength(yj, S); // 推定値用配列確保 for i := 0 to S -1 do if DEFD then yj[i] := 1 / yi[i] else yj[i] := yi[i]; // 行列の作成 データーX^n の組み込み for i := 0 to N -1 do for j := 0 to N -1 do for k := 0 to S - 1 do a[i, j] := a[i,j] + power(xi[k] , i + j); // X^n * Y の組み込み for i := 0 to N - 1 do for k := 0 to S - 1 do a[i, N] := a[i, N] + power(xi[k], i) * yj[k]; // ガウスの消去法実行 gauss(a, xxd, N); // 平均値の計算 my := Mean(yj); // my := Mean(YA); // 相関係数計算 Sy := 0; Syh := 0; for i := 0 to S -1 do begin YhA[i] := xxd[0]; for j := 1 to N -1 do YhA[i] := YhA[i] + xxd[j] * power(Xi[i], j); // 推定値の計算 Sy := Sy + power(yj[i] - my, 2); // データーの分散計算 Syh := Syh + Power(YhA[i] - my, 2); // 推定値の分散計算 end; if Sy > 0 then r := Sqrt(Syh/Sy) // 相関係数計算 else r := 1; LL := '相関係数 r= '+ floatTostrF(r, ffFixed, 2, 3); Memo1.Lines.Add(' '); Memo1.Lines.Add(LL); end; // グリッドの値による補間計算 procedure TForm1.interpolationBtnClick(Sender: TObject); var N, ch, i, j, imax, Z : integer; cn : string; y2, y3 : extended; xd : extended; begin Xin_interpolation.Enabled := False; N := Ninput(false, Z); if N < 0 then begin exit; end; GridSet(N + 1, 3); setlength(x, N); setlength(y, N); SetLength(xx, Z + 1); // 計算結果用配列確保 for i := Low(x) to High(x) do begin val(StringGrid1.cells[1,i + 1], x[i], ch); if ch <> 0 then begin cn := 'x' + intTostr(i + 1) + 'に間違いが有ります。'; application.MessageBox(pchar(cn),'注意',0); break; end; val(StringGrid1.cells[2,i + 1], y[i], ch); if ch <> 0 then begin cn := 'y' + intTostr(i + 1) + 'に間違いが有ります。'; application.MessageBox(pchar(cn),'注意',0); break; end; end; if ch <> 0 then exit; // if not datacheck(x, N) then exit; // xの値に重複が無いか確認 Series1.Clear; // プロット値 Series2.Clear; // テスト計算値 Series3.Clear; // 補間値 Series5.Clear; // 指定点計算値 xmin := x[0]; xmax := x[0]; for i := Low(x) to High(x) do begin if x[i] > xmax then xmax := x[i]; if x[i] < xmin then xmin := x[i]; Series1.AddXY(x[i], y[i]); end; sai(x, y, xx, Z + 1, N); imax := (N - 1) * 40; // 分割数 dx := (xmax - xmin) / imax; for i := 0 to imax do begin xd := dx * i + xmin; y2 := 0; for j := 0 to Z do y2 := y2 + xx[j] * power(xd, j); if DEFD then y2 := 1 / y2; Series3.AddXY(xd, y2); // グラフ表示 if DEF then begin y3 := 0; case radiogroup1.ItemIndex of 1: y3 := f(xd); 2: y3 := f3(xd); 3: y3 := f2(xd); end; Series2.AddXY(xd, y3); // テスト値 end; end; DEF := False; Xin_interpolation.Enabled := True; end; // 指定値からの計算 指定値xによるy補間値計算とグラフ表示 procedure TForm1.Xin_interpolationClick(Sender: TObject); var ch, i, j, Z, ii : integer; xd, y1, y3, xi, gmin, gmax : extended; begin val(Xedit.Text, xd, ch); if ch <> 0 then begin application.MessageBox('xからY推定の入力に間違いが有ります。','注意',0); exit; end; Z := high(xx); Series2.Clear; // テスト値グラフ Series3.Clear; // 補間値グラフ Series5.Clear; // 指定値点 // 最小最大区間グラフ再描画 gmin := xmin; gmax := xmax; if xd < xmin then gmin := xd; if xd > xmax then gmax := xd; ii := round((gmax - gmin) / dx); for j := 0 to ii do begin xi := j * dx + gmin; y3 := 0; for i := 0 to Z do y3 := y3 + xx[i] * power(xi, i); if DEFD then y3 := 1 / y3; Series3.AddXY(xi, y3); end; // 指定値点グラフ追加 指定値xによるy補間値計算とグラフ表示 y1 := 0; for i := 0 to Z do y1 := y1 + xx[i] * power(xd, i); if DEFD then y1 := 1 / y1; Series5.AddXY(xd, y1); end; procedure TForm1.CheckBox2Click(Sender: TObject); begin Xin_interpolation.Enabled := False; end; // グリッド初期設定 procedure TForm1.FormCreate(Sender: TObject); begin FGridSet(101, 3); // 固定行1列1 + 100行2列まで行列を変更しても // 入力値がクリアされないようにします。 GridSet(4, 3); // 最初の設定 end; end.
Lagrange_interpolation.zip
三角関数、逆三角関数、その他関数 に戻る