更新　2022/08/04
　入力値に数字でない間違いがあった場合、その場所の表示がない箇所が多数あったので修正しました。

更新　2017/08/17
１．　楕円の近似式計算でジャスト45°の時円になる対策として、座標変換をし再計算していましたが、問題なく半径を計算できる計算式が分かったので、変更しました。
座標変換は廃止しました。
２．　Delphi XE7で開くときエラーが出るのを修正しました。
３．　自作コンポーネントを使用していたのを廃止しました。

更新　2016/11/25
　楕円の近似式の計算で、楕円の角度が４５°の時、半径ａとｂの寸法が正しく計算されないのを修正しました。
ジャスト４５°になるのは、演算誤差もあるので、めったに起きないのですが、もし起きてしまうと、楕円にならずに、円になってしまいます。
楕円同士の交点検討時、この問題を思い出しました。
交点の計算時、楕円が両方の楕円の角度が ０°４５°であると、正しく交点が計算されないときがあり、対策として、楕円の角度が３０°になるように座標変換をして計算するようにしました。
　最小二乗法で、楕円の二元二次方程式の係数を求めたとき、楕円の半径ａ，ｂを傾き角からｓｉｎとｃｏｓを利用して求めると、４５°の時、正しい値を求めることが出来ません。
最小二乗法で、求める係数が、AX^2 + BXY + CY^2 + DX + EY  の時と X^2 + AXY + BY^2 + CX + DY の時で、どの値が正しく出ないかは、異なりますが、半径はどちらでも、同じように楕円であってもａ　ｂの値が同じになってしまいます。
楕円の角度は、ｓｉｎとｃｏｓを利用しないので、正しい値が出ます。
   X^2 + AXY + BY^2 + CX + DYの係数計算時は、中心座標の演算に、ｓｉｎとｃｏｓの計算を含んでいないので、これも正しい値となり、半径だけが、違った答えとなります。
AX^2 + BXY + CY^2 + DX + EY の時は、正しいのは、楕円の角度だけとなります。
楕円の角度は正しく計算されるので、楕円の角度がゼロ度になるように、座標変換をして計算すれば良い事になります。
　最初角度を得るための、最小二乗法の計算を行い、座標変換後、もう一度最小二乗法の計算後、半径ａ，ｂを計算します。
AX^2 + BXY + CY^2 + DX + EY を最小二乗法で求めた場合は、座標変換後の最小二乗法の計算値から中心座標を求め、元の座標に戻します。

　　近似式の計算

 

　Excelには、グラフ表示に近似式を導き出すルーチンが組み込まれています。
Delphiのプログラムの中でも近似式の計算を使用したいため、色々な近似式計算を集めてみました、コンポーネント化はしていませんが、データーの取り込み方、出力方法を変更すれば容易に使用する事が出来ます。
　ダウンロードをして解凍すると、三点を通る円、行列例（円球の最小二乗法）、多項式近似、楕円最小二乗のフォルダーが解凍されます。
それぞれに、プロジェクトが入っているので、開いて動作を確認してみて下さい。

　三点を通る円


　これは、単純に連立方程式を解けばよいようで、点が三点あるので、二点間を結ぶ直線に直交し、なおかつ中点を通る直線と、もう一つの、点に対する直線の中点を通り、直交する直線が交わる点が円中心となります。
円の半径は、円中心が求まったので、中心から何れかの点までの距離を計算すれば、半径になります。
最小二乗法でも答えは出せます、Excelのソルバーを利用する方法が、インターネットを探すと出てきますが、Delphiでの利用は難しいと思います。
サンプルプログラムの殆どの部分は、グラフ表示に費やしていて、実際の計算部分はほんの僅かです。

　多項式近似

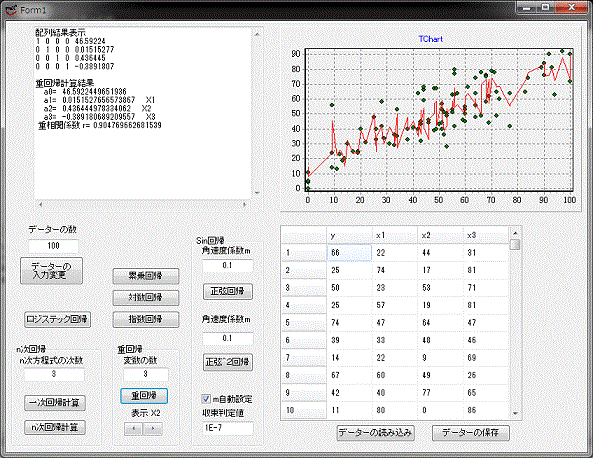
　多項式近似ホルダーの　polynomial.dprojを開いて実行すると、上図のフォームが表示されます。
計算出来るのは、ロジステック、ｎ次回帰、累乗回帰、対数回帰、指数回帰、重回帰、正弦回帰、正弦二乗回帰です。
ロジステック回帰は、値が〇～１の中にないと計算出来ません、それ以外は適当な値でも計算結果はでます。
データーファイルも添付されているので、試してみると良いでしょう。
正弦回帰には、角速度係数が必要なのですが、データーの角速度が小さい場合は、デフォルトの値よりも、角速度係数を小さくしてください。
　計算の手順は、プログラムを見てください、かなりコメントを追加してあるのでわかると思います。
解のもとめ方の詳細については、インターネットで探してください、かなり詳しい説明を見つけることが出来ます。
恐らく、プログラムを作成する場合は、一つか二つ、近似式を組み込めば良いことになるのではないかとおもいます。

　円球の最小二乗法

円と球の近似式を、最小二乗法で求める計算例が、行列例（円球の最小二乗法）フォルダーの中に入っています。
最初は、行列式の計算例として作ったのですが、ついでに、円と球の近似計算を追加しました。
円は、データーとして三点、球は四点以上あれば計算可能です。
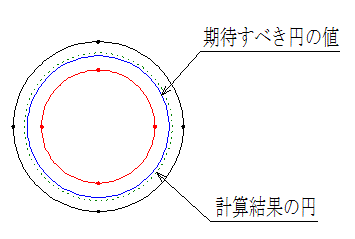　計算の結果の注意点
　上図は、完全な円のデーターを二つ与えて計算した結果を作図して表しています。
一番内側の円と、一番外側の円が、与えた円のデーター、計算結果の円が点線です、期待すべき円というのは、一番内側と、外側の円の調度中間の値の円で、半径の平均値になっていますが、計算される値は、少し大きくなります、これは、半径の二乗が最小になるようにしているからです、Ｅｘｃｅｌのソルバーを利用しても同じ結果になります、Ｌｉｂｒｅｏｆｆｉｃｅに入っているソルバーを利用すると、平均値の半径が計算結果として出ます、Ｅｘｃｅｌとアルゴリズムが違うようです。
確認はしていないのですが、恐らく球の計算でも同じ結果になると思います。
ガウスニュートン法であれば、期待される円の半径が得られます 楕円近似追加 を参照してください。

　楕円の近似式

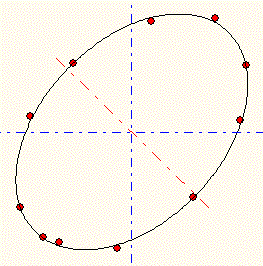
　楕円の近似式計算は、楕円最小二乗のホルダーに入っています。
逆行列が成立しない場合、楕円の答えは正しく出ません、データーの条件によっては、データー数が多くても答えが出せない場合があります。
一応逆行列が成立するか逆行列だけ先に確認をしています。
値がおかしくなるのは、特殊な場合のみで、通常の楕円データーであれば、かなり精度の高い近似式を導き出すことができます。
計算は、最小二乗法で、ガウスの消去法で計算を解いています。
計算の詳細は、インターネットで、楕円　近似　を検索すると見つかるのでそれを参照して下さい。