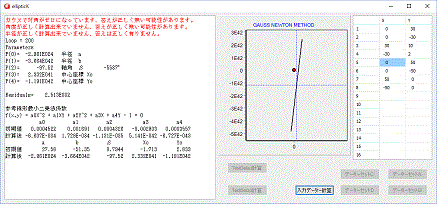
2017/09/04
　演算エラーでプログラムが停止してしまうのを出来るだけなくしました。
入力データーに問題がある場合、決算結果が出ても正しい値ではありません。

2017/08-19
  楕円の角度が45°でも二元二次式から問題なく一般式に変換できる計算方法が判明したので、プログラム修正しました。

2016/11/30　更新
　各種近似式の中の最小二乗法の楕円近似のプログラムの軸角４５°の問題についてこちらのプログラムも同じように修正しました。
入力したデーターによっては、ハングしてしまう現象についても、一応修正を加えました。
elliptic_approximation.dproj　は、通常の非線形最小二乗法ですが、EllipticK_Approximation.dprojの方は、結果が、平均値に近くなるように計算されます。
下図右がEllipticK_Approximation.dprojです。
下図のパターンの円を楕円を最小二乗法で計算すると、対角が０になりなりますが、平均値に近い値が得られる参考パターンとして分かりやすいので、取り上げてみました。

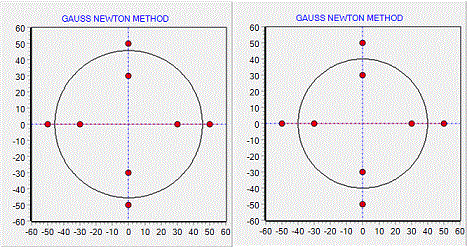
楕円の近似計算の追加

　各種近似式で楕円近似式の計算を紹介していましたが、計算結果に少し疑問が生じたので、新しいのを検討してみました。
新しいのは、http://ikuro-kotaro.sakura.ne.jp/koramu.htm　に紹介されていたものを、Delphi　用に書き直したものです。
元の言語は、Ｎ８８ＢＡＳＩCです。
(今月のコラムの一番下バックナンバー　２００２年　３１，３９，４７　バックナンバー２００３年　　２，３，５を参照)
計算のルーチンのみ取り込んで、グラフィックの部分は各種近似式で使用した部分をそのまま使用しました。
　楕円に近い値を、或いは完全な楕円の値を計算させると、どちらも同じ結果が出ます、但し軸角は９０°違う場合があります。
しかし、楕円に内側に新しい点を対象に追加すると、差が現れます、計算方法の差ともいえます、新しいのは非線形最小二乗法で計算しています。
新しいのには、線形最小二乗法も組み込まれていますが、同じ線形最小二乗法でも、元になった方程式により差が現れるようです。

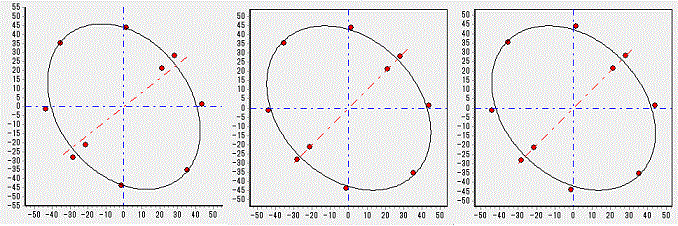
上図の一番左は、各種近似式で紹介した、楕円近似で計算したものです、右の二個は、新しい近似式の結果でガウスニュートン法で計算したものです。
ガウスニュートン法だと、計算に先立って、近似値を与えないと、計算出来ません、近似値は最小二乗法で計算して、更にガウスニュートン法で近似式を計算しています。
ガウスニュートン法だと、計算回数が多くなりますが誤差の推定が出来ます。
詳しい内容は、前記のＵＲＬを参照して下さい。
　上図の結果となる元のデーターは、テスト計算中に見つけた特殊な値で、計算誤差が顕著に現れます。
各種近似式で紹介した、楕円近似だと、軸角が４５°なるべきところが３８．１６°となりかなり外れています。
中央のは、４５°で一番右は、４４．８７°となっています、あくまでも近似式であり、特殊な例なので一般での使用の場合は問題は無いと思いますが。
半径も微妙にそれぞれ違った値となっています。
同じデーターでテスト計算が出来る様に、各種近似式のなかの楕円用にも同じデーターの計算ルーチンを追加しました。
一般的なバラツキのあるデーターの場合、バラツキの範囲内で、上図に現れた傾向が再現される様です。
一番右の図の計算に使用した計算式の場合、データーによっては、計算途中で浮動小数点のオーバーフローが発生します、実際に使用する場合は、オーバーフロー対策を施す必要があるかと思います。
　円の近似についても、同じ様に追加をしました、円の場合は線形最小二乗法なので、特に差はでないようです。