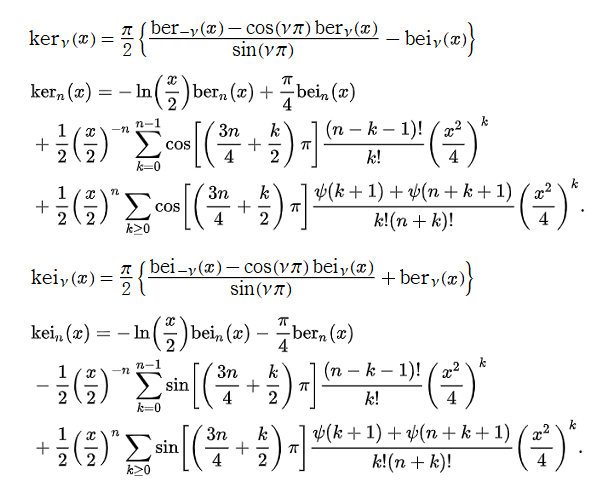左の計算式の場合、xの値の実数は正の値(0≦X)でないと正しい結果は得られません、虚数iの値は正負問題ありません。第1種の計算で、非整数の時、複素数の座標で-45°＜φ≦45°の間でしか計算できませんでしたが、90°～90°の範囲で計算が出来ます。
第1種の非整数が45°～45°の範囲なのに、それを利用した第2種の計算が-90°＜φ≦90°の範囲で正しく計算出来るのが、不思議な感じがします。
検算に利用しているのは、CASIOの計算サイトです。
第３種ケルビン関数
2024/03/31 Σ計算のk乗の計算方法を変更し計算の速度向上。
2024/03/01 第３種追加
第３種は、第２種に 2/(iπ) を乗じるだけなので第２種の計算に追加しました。
ｘの値が複素数の場合の第2、3種ケルビン関数
第2種ケルビン関数の計算には、第1種ケルビン関数の計算が必要です。
第２種ケルビン関数
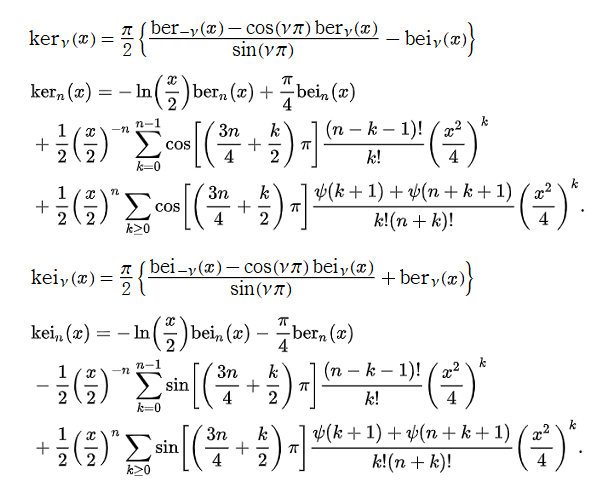左の計算式の場合、xの値の実数は正の値(0≦X)でないと正しい結果は得られません、虚数iの値は正負問題ありません。
第1種の計算で、非整数の時、複素数の座標で-45°＜φ≦45°の間でしか計算できませんでしたが、90°～90°の範囲で計算が出来ます。
第1種の非整数が45°～45°の範囲なのに、それを利用した第2種の計算が-90°＜φ≦90°の範囲で正しく計算出来るのが、不思議な感じがします。
検算に利用しているのは、CASIOの計算サイトです。
第３種ケルビン関数
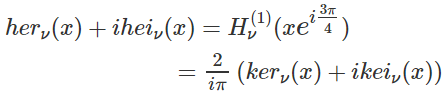計算式はｘの値が複素数でない場合と同じですが、kerv(x)、keiv(x)
の値がそれぞれ複素数なので注意が必用です。
まず a=herv(x), b=heiv(x) （ａ＋ｉｂ） / ｉ として先に処理をします。
（ａ＋ｉｂ） /
ｉ ＝ ｂ－ｉａ (分母のｉを消します)
ｈｅｒｖ（ｘ）＝ (2/π)ｋｅｉｖ（ｘ）
ｈｅｉｖ（ｘ）＝ －(2/π)ｋｅｒｖ（ｘ） となります。
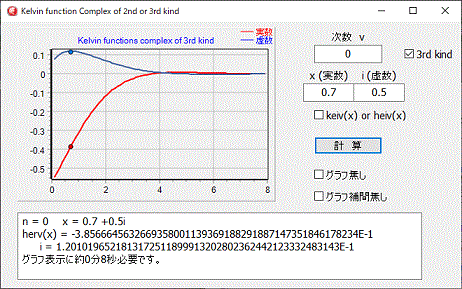Xの値が複素数の場合、計算値は実数部相当の値も、虚数部相当の値も、複素数となるので答えは、実数部相当の値と、虚数部相当の値を別個に表示します。
Xの値の虚数の値がゼロの場合は、第2,3種ケルビン関数のブログラムを使用してください。
３ｒｄ Ｋｉｎｄにチェックを入れると第３種の計算となります、チェックが無ければ第２種です。
プログラム
プログラムには、二種類の多倍長計算が組み込んでありますが、組み込み方は第１種ケルビン関数ｖ，ｘ実数を参照して下さい。
第2種ケルビン関数の計算に必要な第1種ケルビン関数の計算には第1種ケルビン関数v実数,x複素数の中の三個のうちの最後の計算式が一番計算量が少ないので、それを使用しています。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls,
VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs,
VCLTee.Chart, System.Diagnostics, system.UITypes;
type
TForm1 = class(TForm)
Button1: TButton;
Memo1: TMemo;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
Chart1: TChart;
Series1: TLineSeries;
Series2: TLineSeries;
Series3: TPointSeries;
Series4: TPointSeries;
Series5: TLineSeries;
Series6: TLineSeries;
CheckBox1: TCheckBox;
CheckBox2: TCheckBox;
LabeledEdit3: TLabeledEdit;
CheckBox3: TCheckBox;
CheckBox4: TCheckBox;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure FormClose(Sender: TObject; var Action: TCloseAction);
private
{ Private 宣言 }
procedure chart1coment;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
uses system.Math, System.VarCmplx, Velthuis.BigIntegers,mp_real, mp_cmplx, mp_types, mp_base;
{$R *.dfm}
type
DArray = array of double;
var
xt, yt : Darray; // x,y データー akima補間用
m, t : array of mp_float; // m,t akima補間用
BM : array of mp_float; // ベルヌーイ数配列
DG : array of mp_float; // ディガンマ配列
FA : array of mp_float; // 階乗配列
PVG : array of mp_float; // +VΓ
MVG : array of mp_float; // +VΓ
zero, one, two, four : mp_float;
three, pai, log_2pis2 : mp_float;
gamma : mp_float;
thirdF : boolean; // 3rd kind フラグ
const
KMmax = 250; // KM max 250
Vmax = 100; // v 次数 max
GL = 9; // グラフ計算基本点数
// オイラー定数 有効桁分用意
// 0.577215664901532860606512090082402431042159335939923598805767234884867726777664670936947063291746749514631447249807082480960504
// 01448654283622417399764492353625350033374293733773767394279259525824709491600873520394816567085323315177661152862119950150798479374
gstr0 = '0.577215664901532860606512090082402431042159335939923598805767234884867726777664670936947063291746749514631447249807082480960504';
gstr1 = '0144865428362241739976449235362535003337429373377376739427925952582470949160087352039481656708532331517766115286211995015079847';
gstr = gstr0 + gstr1;
//------------------------------------------------------------------------------
NB = 120; // ベルヌーイ数 配列数 NB + 1
var
NumeratorString : array[0..NB] of string; // 分子
DenominatorString : array[0..NB] of string; // 分母
// 最大公約数 ユークリッドの互除法 BigInteger
function gcd_BigInteger(x, y: BigInteger): BigInteger;
var
t : BigInteger;
begin
while y <> 0 do begin
t := x mod y;
x := y;
y := t;
end;
result := x;
end;
// ベルヌーイ数
// Akiyama-Tanigawa algorithm
// BigInteger
procedure Bernoulli_number_BigInteger;
const
n = (NB + 1) * 2;
var
m, j, k : integer;
a : array of BigInteger; // 分子
b : array of BigInteger; // 分母
tmpN : BigInteger; // 分子
tmpD : BigInteger; // 分母
gcd : BigInteger; // 最大公約数
b0 : BigInteger;
begin
setlength(a, n + 1);
setlength(b, n + 1);
k := 0;
for m := 0 to n do begin
a[m] := 1; // 分子 初期値
b[m] := (m + 1); // 分母 初期値
for j := m - 1 downto 0 do begin
tmpN := a[j] * b[j + 1] - a[j + 1] * b[j]; // 分子
tmpN := tmpN * (j + 1); // 〃
tmpD := b[j] * b[j + 1]; // 分母
gcd := gcd_BigInteger(tmpN, tmpD); // 最大公約数
a[j] := tmpN div gcd;
b[j] := tmpD div gcd;
end;
if (m > 0) and (m mod 2 = 0) then begin
b0 := b[0];
b0 := b0 * m * (m -1); // m ベルヌーイ数No
NumeratorString[k] := a[0].tostring;
DenominatorString[k] := b0.tostring;
inc(k);
end;
end;
end;
//------------------------------------------------------------------------------
// ログガンマ多倍長
procedure log_GammaMul(var x, ans : mp_float);
var
v, w : mp_float;
tmp, tmp0, s : mp_float;
i : integer;
begin
mpf_init2(v, w);
mpf_init3(tmp, tmp0, s);
mpf_set1(v);
mpf_set_int(tmp, NB);
while mpf_is_lt(x, tmp) do begin
mpf_mul(v, x, v);
mpf_add(x, one, x);
end;
mpf_mul(x, x, tmp); // x^2
mpf_div(one, tmp, w); // w = 1 / x^2
mpf_set0(s);
for i := NB downto 1 do begin
mpf_add(s, BM[i], tmp); // tmp = s + B[i]
mpf_mul(tmp, w, s); // s = tmp * w
end;
mpf_add(s, BM[0], tmp); // tmp = s + B[0]
mpf_div(tmp, x, s); // s = (s + B[0]) / x
mpf_add(s, log_2pis2, s); // s = s + ln(2π)/2
mpf_ln(v, tmp); // ln(v)
mpf_sub(s, tmp, s); // s := s - ln(v)
mpf_sub(s, x, s); // s := s - x
mpf_div(one, two, tmp); // tmp = 1/2
mpf_sub(x, tmp, tmp0); // tmp0 = x - 1/2
mpf_ln(x, tmp); // ln(x)
mpf_mul(tmp0, tmp, tmp0); // tmp0 = (x - 1/2) * ln(x)
mpf_add(s, tmp0, ans); // ans = s + (x - 1/2) * ln(x)
mpf_clear2(v, w);
mpf_clear3(tmp, tmp0, s);
end;
// 多倍長ガンマ
// xの値が 0 と負整数の時Γは∞になるのですが処理をしていませんのでエラーになります。
// ケルビンの次数が整数の時は使用されません。
procedure gammaMul(var x, ans: mp_float);
var
tmp, tmp0, logG : mp_float;
begin
mpf_init3(tmp, tmp0, logG);
if mpf_is_lt(x, zero) then begin
mpf_mul(pai, x, tmp); // x*π
mpf_sin(tmp, tmp0); // sin(πx);
mpf_sub(one, x, tmp); // 1-x
log_GammaMul(tmp, logG); // loggamma(1-x);
mpf_exp(logG, logG); // exp(logG)
mpf_div(pai, tmp0, tmp); // π/sin(πx)
mpf_div(tmp, logG, ans); // ans = π/(sin(πx) * logG(1-x))
end
else begin
log_GammaMul(x, logG); // logG
mpf_exp(logG, ans); // exp(logG)
end;
mpf_clear3(tmp, tmp0, logG);
end;
//------------------------------------------------------------------------------
// ディガンマ +整数のみ 多倍長
procedure digammaMUL(n: integer; var ans : mp_float);
var
s, tmp : mp_float;
k : integer;
begin
mpf_init2(s, tmp);
n := n - 1;
mpf_set0(s); // Σ=0
mpf_set0(tmp);
if n >= 0 then begin
for k := 1 to n do begin
mpf_set_int(tmp, k);
mpf_div(one, tmp, tmp); // 1 / k
mpf_add(s, tmp, s);
end;
end;
mpf_sub(s, gamma, ans); // Σ + γ
mpf_clear2(s, tmp);
end;
//------------------------------------------------------------------------------
// 階乗 多倍長
procedure factorialMul(n : integer; var ans: mp_float);
label
EXT;
var
i : integer;
bi : mp_float;
begin
mpf_init(bi);
mpf_set1(ans);
mpf_copy(two, bi);
if n <= 1 then begin
goto EXT;
end;
for i := 2 to n do begin
mpf_mul(ans, bi, ans);
mpf_add(bi, one, bi);
end;
EXT:
mpf_clear(bi);
end;
//------------------------------- complex power --------------------------------
// mpc_pow は **.5 時正しい答えを返しません
procedure mpc_powa(x, y : mp_complex; var ans : mp_complex);
var
ay, ai, harf : mp_float;
begin
mpf_init3(ay, ai, harf);
mpc_pow(x, y, ans); // exp(y*ln(x))
// xの虚数部とyの虚数部0なら
if mpf_is0(x.im) and mpf_is0(y.im) then begin
mpf_set0(zero); // 0
mpf_inv(two, harf); // 1/2 0.5
mpf_abs(y.re, ay); // yの実数部の絶対値
mpf_frac(ay, ai); // yの実数部の絶対値の小数部
mpf_sub(ai, harf, ai); // yの実数部の絶対値の小数部と0.5の差分
// 差分がゼロ(yの実数部の小数部が0.5)
if mpf_is0(ai) then
// xの実数部が0と等しいか0より大きいなら
if mpf_is_ge(x.re, zero) then mpf_set0(ans.im) // 答えの虚数部0
// 0より小さいなら
else mpf_set0(ans.re); // 答えの実数部0
mpf_frac(y.re, ai); // 乗数の小数部
if mpf_is0(ai) then mpf_set0(ans.im); // 整数なら答えの虚数部0
end;
// xの整数部とyの虚数部が0なら
if mpf_is0(x.re) and mpf_is0(y.im) then begin
mpf_frac(y.re, ai); // 乗数の小数部
if mpf_is0(ai) then begin // 整数なら
mpf_div(y.re, two, ay); // 偶数奇数確認
mpf_frac(ay, ai); // 小数部
if mpf_is0(ai) then mpf_set0(ans.im) // 偶数なら 虚数部0
else mpf_set0(ans.re) // 奇数なら実数部0
end;
end;
mpf_abs(x.re, ay);
mpf_abs(x.im, ai);
// xの実数部と虚数部の絶対値が等しくてyがゼロでなかったら
if mpf_is_eq(ay, ai) and mpf_is0(y.im) and not mpc_is0(y) then begin
mpf_frac(y.re, ai); // 乗数の小数部
if mpf_is0(ai) then begin // 整数なら
mpf_div(y.re, two, ay); // 偶数奇数確認
mpf_frac(ay, ai); // 小数部
if mpf_is0(ai) then begin
mpf_div(y.re, four, ay); // 4偶数奇数確認
mpf_frac(ay, ai); // 小数部
if mpf_is0(ai) then mpf_set0(ans.im) // 偶数なら 虚数部0
else mpf_set0(ans.re); // 奇数なら 実数部0
end;
end;
end;
mpf_clear3(ay, ai, harf);
end;
//------------------------------------------------------------------------------
// X 値 複素数
// v 次数
// F False berv(z) true beri(z)
procedure berivz(var v : mp_float; var x, ri: mp_complex; F: boolean);
var
k, j : integer;
s, x24k, tmp, tmp0, tmp1 : mp_complex;
kc, xc, xs2: mp_complex;
kd, nd, vk : mp_float;
khg, kf : mp_float;
tmf, tmf0 : mp_float;
sb : mp_complex;
piv3s4, kpis2, pis2: mp_float;
ar, ai, vn : mp_float;
begin
mpc_init5(s, x24k, tmp, tmp0, tmp1);
mpc_init3(kc, xc, xs2);
mpf_init2(khg, kf);
mpf_init3(kd, nd, vk);
mpf_init2(tmf, tmf0);
mpc_init(sb);
mpf_init3(piv3s4, kpis2, pis2);
mpf_init3(ar, ai, vn);
mpf_div(pai, two, pis2); // π/2
mpf_div(pis2, two, tmf); // π/4
mpf_mul(tmf, three, tmf0); // 3π/4
mpf_mul(tmf0, v, piv3s4); // 3πv/4
mpc_set0(s); // Σ=0
mpc_set0(sb);
j := 0;
mpc_div_mpf(x, two, xs2); // x / 2
mpc_mul(xs2, xs2, xc); // (x^2)/ 4
mpc_set1(x24k); // ***
for k := 0 to KMmax do begin
mpf_set1(nd);
mpf_set_int(kf, k); // kf = k
mpf_add(v, kf, tmf0); // k + v
mpf_add(tmf0, one, vk); // vk = k + v + 1;
if mpf_is_lt(vk, zero) then begin // vk < 0 時 nxが整数か確認
mpf_int(vk, tmf); // int(vk);
mpf_sub(vk, tmf, nd); // vk - int(vk) vkが負の整数だったら vk = 0
end;
if mpf_is_ne(vk, zero) and mpf_is_ne(nd, zero) then begin // vkが負の整数の時は計算しない
if mpf_is_ge(v, zero) then
mpf_copy(PVG[k], tmf)
else
mpf_copy(MVG[k], tmf);
mpf_mul(FA[k], tmf, khg); // k!Γ(n+k+1) vkが0,負の整数の時±∞
// mpc_set_mpf(kc, kf, zero); // *** kc = k + 0i 複素数
// mpc_powa(xc, kc, x24k); // *** (i(x^2)/4)^k
mpc_div_mpf(x24k, khg, tmp0); // ((i(x^2)/4)^k)/(k!Γ(v+k+1))
mpf_mul(kf, pis2, kpis2); // kπ/2
mpf_add(piv3s4, kpis2, tmf); // 3πv/4 + kπ/2
if not F then mpf_cos(tmf, tmf0) // cos(3πv/4 + kπ/2)
else mpf_sin(tmf, tmf0); // sin(3πv/4 + kπ/2)
mpc_mul_mpf(tmp0, tmf0, tmp0);
mpc_add(s, tmp0, s); // Σ
mpc_sub(s, sb, tmp0);
if mpc_is0(tmp0) then begin
inc(j);
if j > 3 then break;
end
else j := 0;
mpc_copy(s, sb);
end;
mpc_mul(x24k, xc, x124k); // ***
end;
mpc_set_mpf(tmp, v, zero); // v + 0i
// x が0で次数vが負数の時power演算ゼロでの除算防止
if mpc_is0(x) and mpf_is_lt(v, zero) then // V<0 x=0 時は無限大になるので計算しない
else begin
mpc_powa(xs2, tmp, tmp0); // (x/2)^v
mpc_mul(s, tmp0, s); // (x/2)^v * Σ
end;
mpc_copy(s, ri);
mpf_abs(x.re, ar);
mpf_abs(x.im, ai);
mpf_frac(v, vn);
// xの実数部と虚数部の絶対値が等しく次数が整数だったら
if mpf_is_eq(ar, ai) and mpf_is0(vn) then begin
mpf_div(v, two, ar);
mpf_frac(ar, ai);
if mpf_is0(ai) then // 次数が偶数だったら
if not F then mpf_set0(ri.im)
else mpf_set0(ri.re);
end;
// xの虚数部がゼロだったら
if mpf_is0(x.im) then mpf_set0(ri.im);
// xの実数部がゼロだったら
if mpf_is0(x.re) and not mpf_is0(x.im) then begin
mpf_frac(v, ar);
if mpf_is0(ar) then begin // 次数整数だったら
mpf_div(v, two, ai);
mpf_frac(ai, ar);
if mpf_is0(ar) then mpf_set0(ri.im) // 次数偶数だったら
else mpf_set0(ri.re); // 次数奇数だったら
end
end;
mpc_clear5(s, x24k, tmp, tmp0, tmp1);
mpc_clear3(kc, xc, xs2);
mpf_clear2(khg, kf);
mpf_clear3(kd, nd, vk);
mpf_clear2(tmf, tmf0);
mpc_clear(sb);
mpf_clear3(piv3s4, kpis2, pis2);
mpf_clear3(ar, ai, vn);
end;
// v 非整数
// X 値 複素数
// v 次数
// F False kerv(z) true keri(z)
procedure fractional(var v : mp_float; var x, ri: mp_complex; F: boolean);
var
bervz, beivz : mp_complex;
bermv, beimv : mp_complex;
cosvpi, sinvpi : mp_float;
tmpc0, tmpc1 : mp_complex;
tmpf : mp_float;
begin
mpc_init2(bervz, beivz);
mpc_init2(bermv, beimv);
mpf_init3(cosvpi, sinvpi, tmpf);
mpc_init2(tmpc0, tmpc1);
berivz(v, x, bervz, false); // berv(z)
berivz(v, x, beivz, true); // beiv(z)
mpf_chs(v, tmpf);
berivz(tmpf, x, bermv, false); // ber-v(z)
berivz(tmpf, x, beimv, true); // bei-v(z)
mpf_mul(v, pai, tmpf); // vπ
mpf_cos(tmpf, cosvpi); // cos(vπ)
mpf_sin(tmpf, sinvpi); // sin(vπ)
if not F then begin
mpc_mul_mpf(bervz, cosvpi, tmpc0); // tmpc0 = cos(vπ) berv(z)
mpc_sub(bermv, tmpc0, tmpc1); // tmpc1 = ber-v(z) - cos(vπ) berv(z)
mpc_div_mpf(tmpc1, sinvpi, tmpc0); // tmpc0 = (ber-v(z) - cos(vπ) berv(z)) / sin(vπ)
mpc_sub(tmpc0, beivz, tmpc1); // (ber-v(z) - cos(vπ) berv(z)) / sin(vπ) - beiv(z)
end
else begin
mpc_mul_mpf(beivz, cosvpi, tmpc0); // tmpc0 = cos(vπ) beiv(z)
mpc_sub(beimv, tmpc0, tmpc1); // tmpc1 = bei-v(z) - cos(vπ) beiv(z)
mpc_div_mpf(tmpc1, sinvpi, tmpc0); // tmpc0 = (bei-v(z) - cos(vπ) beiv(z)) / sin(vπ)
mpc_add(tmpc0, bervz, tmpc1); // (bei-v(z) - cos(vπ) beiv(z)) / sin(vπ) + berv(z)
end;
mpc_mul_mpf(tmpc1, pai, tmpc0); // + pi
mpc_div_mpf(tmpc0, two, ri); // /2
mpc_clear2(bervz, beivz);
mpc_clear2(bermv, beimv);
mpf_clear3(cosvpi, sinvpi, tmpf);
mpc_clear2(tmpc0, tmpc1);
end;
// v 整数 n
// X 値 複素数
// v 次数
// F False kerv(z) true keri(z)
procedure integers(var v : mp_float; var x, ri: mp_complex; F: boolean);
var
k, ni, j : integer;
nd : double;
nc : mp_complex; // ***
bervx, beivx : mp_complex;
xs2, xh2s4, xh2s4hk : mp_complex; // x/2, x^2/4 ,(x^2/4)^k
pis4 : mp_float; // π/4
lnxs2 : mp_complex; // ln(x/2)
mlnxs2berix, pis4berix : mp_complex; // ln(x/2)berivx, (π/4)berix
n3s4, ks2, n3s4Pks2, n3s4Pks2pi: mp_float; // 3n/4, k/2, 3n/4+k/2, (3n/4+k/2)π
cossin : mp_float; // cossin((3n/4+k/2)π)
nmkm1ska : mp_float; // (n-k-1)1/k!
psis : mp_float; // Ψ(k+1),Ψ(n+k+1), Ψ(k+1)+Ψ(n+k+1)
kf, khnpkh : mp_float; // k!(n+k)!
snm1, sninf, sninfback : mp_complex; // Σn-1, Σ∞
tmf0, tmf1, av : mp_float;
tmc0, tmc1 : mp_complex;
kernx, keinx : mp_complex;
begin
mpc_init3(nc, bervx, beivx); // ***
mpc_init3(xs2, xh2s4, xh2s4hk);
mpf_init(pis4);
mpc_init(lnxs2);
mpc_iniT2(mlnxs2berix, pis4berix);
mpf_init4(n3s4, ks2, n3s4Pks2, n3s4Pks2pi);
mpf_init3(cossin, nmkm1ska, psis);
mpf_init2(kf, khnpkh);
mpc_init3(snm1, sninf, sninfback);
mpf_init3(tmf0, tmf1, av);
mpc_init2(tmc0, tmc1);
mpc_init2(kernx, keinx);
mpf_abs(v, av); // |v|
nd := mpf_todouble(av); // v->double nd
ni := round(nd); // nd-> integer ni
mpc_set_mpf(nc, av, zero); // v-> cmplex nc
mpc_div_mpf(x, two, xs2); // xs2 = x/2
mpc_mul(xs2, xs2, xh2s4); // x^2/4 = (x/2)^2
mpf_div(pai, four, pis4); // π/4
mpf_mul(three, av, n3s4); // 3n n=v
mpf_div(n3s4, four, n3s4); // 3n/4
mpc_ln(xs2, lnxs2); // ln(x/2)
mpc_chs(lnxs2, lnxs2); // -ln(x/2)
berivz(av, x, bervx, false); // bervx
berivz(av, x, beivx, true); // berix
mpc_set1(xh2s4hk); // ***
if not F then begin
mpc_mul(bervx, lnxs2, mlnxs2berix); // ln(x/2) bervx
mpc_mul_mpf(beivx, pis4, pis4berix); // π/4 beivx
mpc_add(mlnxs2berix, pis4berix, kernx); // kern(x) = -ln(x/2) bervx + π/4 beivx
end
else begin
mpc_mul(beivx, lnxs2, mlnxs2berix); // ln(x/2) beivx
mpc_mul_mpf(bervx, pis4, pis4berix); // π/4 bervx
mpc_sub(mlnxs2berix, pis4berix, keinx); // kein(x) = -ln(x/2) beivx - π/4 bervx
end;
mpc_set0(snm1);
for k := 0 to ni - 1 do begin
mpf_set_int(kf, k); // mp_float k
mpf_div(kf, two, ks2); // k/2
mpf_add(n3s4, ks2, n3s4Pks2); // 3n/4 + k/2
mpf_mul(n3s4Pks2, pai, n3s4Pks2pi); // (3n/4 + k/2)π
if not F then
mpf_cos(n3s4Pks2pi, cossin) // cos(((3n/4 + k/2)π)
else
mpf_sin(n3s4Pks2pi, cossin); // cos(((3n/4 + k/2)π)
// mpc_set_mpf(kc, kf, zero); // *** complex k
// mpc_powa(xh2s4, kc, xh2s4hk); // *** (x^2/4)^k
mpf_mul(cossin, FA[ni - k - 1], tmf1); // cos(((3n/4 + k/2)π) * (n-k-1)!
mpf_div(tmf1, FA[k], tmf1); // cos(((3n/4 + k/2)π) * (n-k-1)! / k!
mpc_mul_mpf(xh2s4hk, tmf1, tmc0); // cosαβ * (x^2/4)^k
mpc_add(snm1, tmc0, snm1); // Σ1
mpc_mul(xh2s4hk, xh2s4, xh2s4hk); // ***
end;
mpc_chs(nc, tmc0); // -n
mpc_powa(xs2, tmc0, tmc1); // (x/2)^-n
mpc_mul(snm1, tmc1, snm1); // Σ1 * (x/2)^-n
mpc_div_mpf(snm1, two, snm1); // Σ1 * (x/2)^-n / 2
j := 0;
mpc_set0(sninf);
mpc_set0(sninfback);
mpc_set1(xh2s4hk); // ***
for k := 0 to KMmax do begin
mpf_set_int(kf, k); // mp_float k
mpf_div(kf, two, ks2); // k/2
mpf_add(n3s4, ks2, n3s4Pks2); // 3n/4 + k/2
mpf_mul(n3s4Pks2, pai, n3s4Pks2pi); // (3n/4 + k/2)π
if not F then
mpf_cos(n3s4Pks2pi, cossin) // cos(((3n/4 + k/2)π)
else
mpf_sin(n3s4Pks2pi, cossin); // sin(((3n/4 + k/2)π)
// mpc_set_mpf(kc, kf, zero); // *** complex k
// mpc_powa(xh2s4, kc, xh2s4hk); // *** (x^2/4)^k
mpf_copy(DG[ni + k + 1], tmf0); // Ψ(n+k+1)
mpf_add(DG[k + 1], tmf0, psis); // psis = Ψ(k+1)+Ψ(n+k+1)
mpf_mul(FA[k], FA[ni + k], khnpkh); // k!(n+k)!
mpf_mul(cossin, psis, tmf0); // cos or sin(((3n/4 + k/2)π) * (Ψ(k+1)+Ψ(n+k+1))
mpf_div(tmf0, khnpkh, tmf1); // cos or sin α/ (k!(n+k)!)
mpc_mul_mpf(xh2s4hk, tmf1, tmc0); // cos or sin αβ * (x^2/4)^k
mpc_add(sninf, tmc0, sninf); // Σ2
mpc_sub(sninf, sninfback, tmc1); // 収束判定 収束=tmc1
if mpc_is0(tmc1) then inc(j)
else j := 0;
if j > 2 then break;
mpc_copy(sninf, sninfback);
mpc_mul(xh2s4hk, xh2s4, xh2s4hk); // ***
end;
mpc_powa(xs2, nc, tmc1); // (x/2)^n
mpc_mul(sninf, tmc1, sninf); // Σ2 * (x/2)^n
mpc_div_mpf(sninf, two, sninf); // Σ2 * (x/2)^n/2
if not F then
mpc_add(kernx, snm1, tmc0) // A + Σ1
else
mpc_sub(keinx, snm1, tmc0); // A - Σ1
mpc_add(tmc0, sninf, ri); // A + or - Σ1 + Σ2
// v<0 なら -1^|v| * ri
if (not s_mpf_is_ge0(v)) and (ni mod 2 <> 0) then mpc_chs(ri, ri);
mpc_clear3(nc, bervx, beivx); // ***
mpc_clear3(xs2, xh2s4, xh2s4hk);
mpf_clear(pis4);
mpc_clear(lnxs2);
mpc_clear2(mlnxs2berix, pis4berix);
mpf_clear4(n3s4, ks2, n3s4Pks2, n3s4Pks2pi);
mpf_clear3(cossin, nmkm1ska, psis);
mpf_clear2(kf, khnpkh);
mpc_clear3(snm1, sninf, sninfback);
mpf_clear3(tmf0, tmf1, av);
mpc_clear2(tmc0, tmc1);
mpc_clear2(kernx, keinx);
end;
// 整数非整数
// X 値 複素数
// v 次数
// 第2種 F False kerv(z) true keri(z)
// thirdF False 第2種 true 第3種
// 第3種 2/(iπ) * (kerv + ikeiv)
procedure kerviz(var v : mp_float; var x, ri: mp_complex; F: boolean);
var
vi, twospi : mp_float;
begin
mpf_init2(vi, twospi);
mpf_div(two, pai, twospi); // 2/π
mpf_frac(v, vi); // vの 小数部vi
// 第3種の場合実数相当部と虚数部相当部入れ替えて計算します 2/(iπ) * (kerv + ikeiv)
// 1/(0+i) * (kerv + ikeiv) の処理 虚数相当部と実数相当部が入れ替わります
// (kerv + ikeiv)/(0+i) -> (kerv + ikeiv)i/((0+i)i) -> (ikerv - keiv)/-1
// -> (keiv - ikerv) ※ (keiv - ikerv) * 2/π
// ※ herv = keiv * 2/π heiv = -kerv * 2/π
if thirdF then if F then F := False // 第3種だったら実数虚数部フラグ反転
else F := True; // 虚数部と実数部入れ替え
if mpf_is0(vi) then integers(v, x, ri, F) // 整数計算
else fractional(v, x, ri, F); // 非整数計算
if thirdF then begin // 第3種だったら
mpc_mul_mpf(ri, twospi, ri); // 2/π 乗算
if not F then mpc_chs(ri, ri); // 第三種の場合フラグ反転に注意 虚数相当部の符号反転
end;
mpf_clear2(vi, twospi);
end;
// akima m,t テーブル作成
// x[] xデーター配列
// y[] yデーター配列
// m[] m係数テーブル
// t[] t係数テーブル
procedure akima_table;
var
ii, n : integer;
a, b, half, tmf, tmf0 : mp_float;
ytm, xtm : array of mp_float;
tmf1 : mp_float;
begin
n := high(xt) + 1;
setlength(ytm, n);
setlength(xtm, n);
for ii := 0 to n - 1 do begin
mpf_init(ytm[ii]);
mpf_init(xtm[ii]);
end;
mpf_init5(a, b, half, tmf, tmf0);
mpf_init(tmf1);
mpf_set_dbl(half, 1 / 2);
// mpf_set_int(tow, 2);
// mpf_set0(zero);
for ii := 0 to n -1 do begin
mpf_set_dbl(xtm[ii], xt[ii]);
mpf_set_dbl(ytm[ii], yt[ii]);
end;
// shift data by + 2 in the array and compute the secants
// also calculate extrapolated and end point secants
// 傾斜α両端を除く Δy/Δx
for ii := 0 to n - 2 do begin
mpf_sub(ytm[ii + 1], ytm[ii], tmf);
mpf_sub(xtm[ii + 1], xtm[ii], tmf0);
mpf_div(tmf, tmf0, m[ii + 2]);
end;
// for ii := 0 to n - 2 do
// m[ii + 2] := (yt[ii + 1] - yt[ii]) / (xt[ii + 1] - xt[ii]);
// 端点傾斜処理
mpf_mul(two, m[2], tmf);
mpf_sub(tmf, m[3], m[1]);
// m[1] := 2 * m[2] - m[3];
mpf_mul(two, m[1], tmf);
mpf_sub(tmf, m[2], m[0]);
// m[0] := 2 * m[1] - m[2];
mpf_mul(two, m[n], tmf);
mpf_sub(tmf, m[n - 1], m[n + 1]);
// m[n + 1] := 2 * m[n] - m[n - 1];
mpf_mul(two, m[n + 1], tmf);
mpf_sub(tmf, m[n], m[n + 2]);
// m[n + 2] := 2 * m[n + 1] - m[n];
// 各ポイントの傾斜係数計算
for ii := 0 to n - 1 do begin
mpf_sub(m[ii + 3],m[ii + 2],tmf0);
mpf_abs(tmf0, a);
// a := abs(m[ii + 3] - m[ii + 2]);
mpf_sub(m[ii + 1], m[ii], tmf0);
mpf_abs(tmf0, b);
// b := abs(m[ii + 1] - m[ii]);
mpf_add(a, b, tmf1);
if mpf_is_ne(tmf1, zero) then begin
mpf_mul(a, m[ii + 1], tmf);
mpf_mul(b, m[ii + 2], tmf0);
mpf_add(tmf, tmf0, tmf);
mpf_div(tmf, tmf1, t[ii]);
end
else begin
mpf_add(m[ii + 2], m[ii + 1], tmf);
mpf_mul(half, tmf, t[ii]);
end;
{
if (a + b) <> 0 then begin
t[ii] := (a * m[ii + 1] + b * m[ii + 2]) / (a + b);
end
else
t[ii] := half * (m[ii + 2] + m[ii + 1]);
}
end;
for ii := 0 to n - 1 do begin
mpf_clear(ytm[ii]);
mpf_clear(xtm[ii]);
end;
mpf_clear5(a, b, half, tmf, tmf0);
mpf_clear(tmf1);
end;
// akima 補間値計算
// xx xの値
// x[] xデーター配列
// y[] yデーター配列
// m[] m係数テーブル
// t[] t係数テーブル
// result 補間値y'
function akima_Interpolation(xx: double): double;
var
iB, iM, iT: integer;
a, b, tmf, tmf0 : mp_float;
c, d, e, f, tmf1 : mp_float;
three : mp_float;
begin
mpf_init4(a, b, tmf, tmf0);
mpf_init5(c, d, e, f, tmf1);
mpf_init(three);
mpf_set_int(three, 3);
iB := low(xt); // x[] bottom 配列no
iT := high(xt); // x[] top配列No
// xx値の上下の配列xの配列番号を探す
// XX<x[iB]の場合一番下の区間 XX>x[iT]の場合一番上の区間
while (iT - iB) > 1 do begin
iM := (iB + iT) div 2; // middle配列no
if xt[iM] > xx then
iT := iM
else
iB := iM;
end;
mpf_set_dbl(b, xt[iT] - xt[iB]);
// b := xt[iT] - xt[iB]; // 区間のxの変化量
mpf_set_dbl(a, xx - xt[iB]);
// a := xx - xt[iB]; // x[iB]からのxの値
// 3次akima spline 計算
mpf_set_dbl(c, yt[iB]); // c = yt[ib]
mpf_mul(t[iB], a, d); // d = t[ib] * a
mpf_mul(three, m[iB + 2], tmf); // 3 * m[iB + 2]
mpf_mul(two, t[ib], tmf0); // 2 * t[iB]
mpf_sub(tmf, tmf0, tmf1); // 3 * m[iB + 2] - 2 * t[iB]
mpf_sub(tmf1, t[iB + 1], tmf); // 3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]
mpf_mul(tmf, a, tmf); // (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a
mpf_mul(tmf, a, tmf); // (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a * a
mpf_div(tmf, b, e); // (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a * a / b
mpf_add(t[iB], t[iB + 1], tmf); // t[iB] + t[iB + 1]
mpf_mul(two, m[iB + 2], tmf0); // 2 * m[iB + 2]
mpf_sub(tmf, tmf0, tmf); // t[iB] + t[iB + 1] - 2 * m[iB + 2]
mpf_mul(tmf, a, tmf); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a
mpf_mul(tmf, a, tmf); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a
mpf_mul(tmf, a, tmf); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a * a
mpf_mul(b, b, tmf0); // b * b
mpf_div(tmf, tmf0, f); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a * a / (b * b)
mpf_add(c, d, tmf); // c + d
mpf_add(tmf, e, tmf); // c + d + e
mpf_add(tmf, f, tmf); // c + d + e + f
result := mpf_todouble(tmf);
{
result := yt[iB]
+ t[iB] * a
+ (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a * a / b
+ (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a * a / (b * b);
}
mpf_clear4(a, b, tmf, tmf0);
mpf_clear5(c, d, e, f, tmf1);
mpf_clear(three);
end;
procedure ChartBackclear; // ***
begin
with Form1.Chart1.BackImage.Bitmap.Canvas do begin
Brush.Color := clBtnFace;
Brush.Style := bsSolid;
FillRect(rect(0, 0, Form1.Chart1.Width, Form1.Chart1.Height));
Brush.Style := bsClear;
end;
end;
procedure TForm1.chart1coment; // ***
begin
with Form1.Chart1.BackImage.Bitmap.Canvas do begin
Font.Size := 8;
Font.Style := [];
Font.Color := clred;
TextOut(chart1.Width - 30, 1,'実数');
Font.Color := clblue;
TextOut(chart1.Width - 30, 13,'虚数');
Pen.Width := 1;
Pen.Color := clred;
MoveTo(chart1.Width - 50, 6);
LineTo(chart1.Width - 32, 6);
Pen.Color := clblue;
MoveTo(chart1.Width - 50, 18);
LineTo(chart1.Width - 32, 18);
end;
end;
// 計算
// xの値が大きくなると誤差が大きくなります。
// x実数の値がX<0の時は正しい値がでません
// ta[]グラフ用計算点
procedure TForm1.Button1Click(Sender: TObject);
label
EXT;
const
x0m = 1e-50; // ゼロ近傍値 infinty の符号設定計算値
ta : array[0..GL - 1] of double = (0.08, 0.14, 0.23, 0.46, 0.86, 1.5, 2.5, 3.2, 4);
YPM = 1E304; // Double 演算オーバーフロー対策 最大値制限値
YMM = - YPM;
zeromg = '1E-90'; // 計算結果表示これより小さい値は0にします 演算桁数の1/2
var
ch, i, xi: integer;
kerx, keix: double;
kerxe, keixe: double;
xin, vin, xv : double;
xmin, xmax, dx, dxf : double;
ymin, ymax: double;
kerl : Darray;
keil : Darray;
xl : Darray;
xm, vm, xvm, ixm: mp_float;
nd, tmf : mp_float;
ri : mp_complex;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
mm, ss, ms : integer;
xc, xcb, dxc : mp_complex;
GS : integer; // xv = 0 がない場合 推定点数
k : integer;
vk, avm, tmf0, zz : mp_float;
ix : double;
istr : string;
F : boolean;
// double to mpc グラフ計算用
procedure xvtoXc(xv, ia : double; var xc : mp_complex);
begin
mpf_set_dbl(xvm, xv);
mpf_set_dbl(tmf, ia);
mpc_set_mpf(xc, xvm, tmf);
end;
function maxmin(x : double): double;
begin
result := x;
if x > YPM then result := YPM;
if x < YMM then result := YMM;
end;
begin
memo1.Clear;
val(labelededit1.Text, vin, ch);
if ch <> 0 then begin
application.MessageBox('次数vの値に間違いがあります。','注意', 0);
exit;
end;
if abs(vin) > Vmax then begin
application.MessageBox('次数vの値が計算範囲外です。','注意', 0);
exit;
end;
val(labelededit2.Text, xin, ch);
if ch <> 0 then begin
application.MessageBox('xの値に間違いがあります。','注意', 0);
exit;
end;
if abs(xin) > 100 then begin
application.MessageBox('xが100を越えると条件によって誤差が大きくなります。','注意', 0);
end;
val(labelededit3.Text, ix, ch);
if ch <> 0 then begin
application.MessageBox('i の値に間違いがあります。','注意', 0);
exit;
end;
if abs(ix) > 100 then begin
application.MessageBox('iが100を越えると条件によって誤差が大きくなります。','注意', 0);
end;
xmin := 0;
if xin < 0 then begin
istr := 'xの値がx≧0でないと' + #13#10 +
'正しい答えが得られません計算を中断しますか';
if MessageDlg(istr , mtConfirmation, [mbYes, mbNo], 0, mbYes) = mrYes then exit;
xmin := xin - 0.1;
end;
mpf_init4(xm, vm, xvm, ixm);
mpf_init3(nd, tmf, zz);
mpf_init3(vk, avm, tmf0);
mpc_init4(ri, xc, xcb, dxc);
ChartBackclear; // ***
F := False; // kerx 計算
if Checkbox3.Checked = true then F := true; // keix 計算
if checkbox4.Checked = true then begin
thirdF := true;
Chart1.Title.Caption := 'Kelvin functions complex of 3rd kind';
end
else begin
thirdF := false;
Chart1.Title.Caption := 'Kelvin functions complex of 2nd kind';
end;
mpf_set0(ixm);
mpf_read_decimal(vm, PAnsiChar(ansistring(labelededit1.Text + #00)));
mpf_read_decimal(xm, PAnsiChar(ansistring(labelededit2.Text + #00)));
mpf_read_decimal(ixm, PAnsiChar(ansistring(labelededit3.Text + #00)));
mpf_read_decimal(zz, PAnsiChar(ansistring(zeromg + #00)));
mpc_set_mpf(xcb, xm, ixm); // xcb 計算用 xの複素数
series1.Clear;
series2.Clear;
series3.Clear;
series4.Clear;
if ix >= 0 then istr := ' +' + floatTostr(ix) + 'i'
else istr := ' ' + floatTostr(ix) + 'i';
memo1.Lines.Append('n = ' + floatTostr(vin) + ' x = ' + floatTostr(xin) + istr);
application.ProcessMessages;
mpf_abs(vm, avm);
for k := 0 to KMmax do begin
mpf_set_int(tmf, k); // k
mpf_add(tmf, avm, tmf0); // v + k
mpf_add(tmf0, one, vk); // vk= v + k + 1
gammaMul(vk, PVG[k]); // Γ(n+k+1)
end;
mpf_chs(avm, avm); // -v
for k := 0 to KMmax do begin
mpf_set1(nd);
mpf_set_int(tmf, k); // k
mpf_add(tmf, avm, tmf0); // -v + k
mpf_add(tmf0, one, vk); // vk= -v + k + 1
if mpf_is_lt(vk, zero) then begin // vk < 0 時 nxが整数か確認
mpf_int(vk, tmf); // int(vk);
mpf_sub(vk, tmf, nd); // vk - int(vk) vkが負の整数だったら nd = 0
end;
if mpf_is_ne(vk, zero) and mpf_is_ne(nd, zero) then // vkが負の整数の時は計算しない
gammaMul(vk, MVG[k]) // Γ(n+k+1)
else
mpf_set0(MVG[k]); // Γ(n+k+1) = 0
end;
StopWatch := TStopwatch.StartNew;
kerxe := 0;
keixe := 0;
// 表示値の計算
if not mpc_is0(xcb) then begin
kerviz(vm, xcb, ri, F); // xcb 複素数
kerxe := mpf_todouble(ri.re);
keixe := mpf_todouble(ri.im);
if checkbox3.Checked = false then begin
if not thirdF then
memo1.Lines.Append( string('kerv(x) = ' + mpf_decimal(ri.re, 50))) // 数値表示
else
memo1.Lines.Append( string('herv(x) = ' + mpf_decimal(ri.re, 50))); // 数値表示
if not mpf_is0(ixm) then
memo1.Lines.Append( string(' i = ' + mpf_decimal(ri.im, 50))); // 数値表示
end
else begin
if not thirdF then
memo1.Lines.Append( string('keiv(x) = ' + mpf_decimal(ri.re, 50))) // 数値表示
else
memo1.Lines.Append( string('heiv(x) = ' + mpf_decimal(ri.re, 50))); // 数値表示
if not mpf_is0(ixm) then
memo1.Lines.Append( string(' i = ' + mpf_decimal(ri.im, 50))); // 数値表示
end;
end
// xc=0 v > 0 の場合 r ±∞ i ±∞
// xc=0 v = 0 の場合 r ∞ i -π/4
// xc=0 v = 0 の場合 r 0.5 i ∞
else begin
mpc_set_dbl(dxc, x0m, 0);
kerviz(vm, dxc, ri, F); // dxc 複素数 0近傍計算
if s_mpf_is_ge0(ri.re) then kerxe := infinity
else kerxe := -infinity;
if s_mpf_is_ge0(ri.re) then keixe := infinity // ri.im は x の虚数部が0でないとき
else keixe := -infinity;
if mpf_is0(vm) then begin // v=0
if not thirdF then begin
if checkbox3.Checked = false then begin
kerxe := infinity;
memo1.Lines.Append('kerv(x) = ' + floattostr(kerxe)); // 数値表示
end
else begin
mpf_div(pai, four, tmf);
mpf_chs(tmf, tmf);
keixe := -pi / 4;
memo1.Lines.Append('keiv(x) = ' + string(mpf_decimal(tmf, 50))); // 数値表示
end;
end
else begin
if checkbox3.Checked = false then begin
mpf_div(one, two, tmf);
mpf_chs(tmf, tmf);
memo1.Lines.Append('herv(x) = ' + string((mpf_decimal(tmf, 50)))); // 数値表示
end
else begin
keixe := -infinity;
memo1.Lines.Append('heiv(x) = ' + floattostr(keixe)); // 数値表示
end;
end;
end
else begin // v <> 0
mpf_abs(vm, tmf);
if mpf_is_eq(tmf, two) then begin // v = 2
if not thirdF then begin
kerxe := 0.5;
keixe := infinity;
if checkbox3.Checked = false then // V-2, V<>0
memo1.Lines.Append('kerv(x) = ' + floattostr(kerxe)) // 数値表示
else
memo1.Lines.Append('keiv(x) = ' + floattostr(keixe)); // 数値表示
end
else begin
kerxe := infinity;
mpf_div(one, pai, tmf);
mpf_chs(tmf, tmf);
if checkbox3.Checked = false then // V-2, V<>0
memo1.Lines.Append('herv(x) = ' + floattostr(kerxe)) // 数値表示
else
memo1.Lines.Append('herv(x) = ' + string((mpf_decimal(tmf, 50)))); // 数値表示
end;
end
else begin
if not thirdF then begin
if checkbox3.Checked = false then // V-2, V<>0
memo1.Lines.Append('kerv(x) = ' + floattostr(kerxe)) // 数値表示
else
memo1.Lines.Append('keiv(x) = ' + floattostr(keixe)); // 数値表示
end
else begin
if checkbox3.Checked = false then // V-2, V<>0
memo1.Lines.Append('herv(x) = ' + floattostr(kerxe)) // 数値表示
else
memo1.Lines.Append('heiv(x) = ' + floattostr(keixe)); // 数値表示
end;
end;
end;
end;
StopWatch.Stop;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
ms := ElapsedMillseconds * (GL + 1) * 2 + 1000; // ***
mm := ms div 60000;
ss := (ms mod 60000) div 1000;
memo1.Lines.Append('グラフ表示に約' + inttostr(mm) + '分' + inttostr(ss) + '秒必要です。');
if checkbox2.Checked = true then begin // グラフ無だったら終了
Chart1.Canvas.Font.Style := [fsBold];
Chart1.Canvas.Font.size := 8;
Chart1.Canvas.TextOut(170, 115,'グラフ無し');
goto EXT;
end;
// 最大値最小値の検索とグラフデーター作成
xi := Trunc(xin);
// xmin := 0;
if xi > 4 then xmin := xi - 4;
xmax := xmin + 8;
setlength(kerl, GL + GL);
setlength(keil, GL + GL);
setlength(xt, GL + GL); setlength(yt, GL + GL);
setlength(xl, GL + GL);
dxf := 0.1;
dx := 0.1;
dx := (xmax - xmin) / (Gl + GL - 1);
for i := 0 to GL + GL - 1 do xl[i] := dx * i + xmin;
xl[0] := xl[0] + dxf;
xl[GL + GL - 1] := xl[GL + GL - 1] - dxf;
GS := 80;
// グラフ用データー作成
ymin := 0;
ymax := 0;
for i := 0 to GL + GL - 1 do begin
xv := xl[i];
xvtoxc(xv, ix, xc);
kerviz(vm, xc, ri, F);
kerl[i] := maxmin(mpf_todouble(ri.re));
keil[i] := maxmin(mpf_todouble(ri.im));
if kerl[i] > ymax then ymax := kerl[i];
if keil[i] > ymax then ymax := keil[i];
if kerl[i] < ymin then ymin := kerl[i];
if keil[i] < ymin then ymin := keil[i];
end;
// 指定値の値制御
if kerxe > ymax then kerxe := ymax;
if kerxe < ymin then kerxe := ymin;
if keixe > ymax then keixe := ymax;
if keixe < ymin then keixe := ymin;
series3.AddXY(xin, kerxe); // 実数部計算点ドット
if not mpf_is0(ixm) then // 虚数部0だったら虚数ドット無し
series4.AddXY(xin, keixe);
if checkbox1.Checked = true then begin
for i := 0 to GL + GL - 1 do series1.AddXY(xl[i], kerl[i]);
if not mpf_is0(ixm) then // 虚数部0だったら虚数部グラフ無し
for i := 0 to GL + GL - 1 do series2.AddXY(xl[i], keil[i]);
end;
if checkbox1.Checked = false then begin
// グラフ計算
for i := 0 to GL + GL - 1 do begin
xt[i] := xl[i];
yt[i] := kerl[i];
end;
akima_table;
dx := (xt[GL + GL - 1] - xt[0]) / GS;
for i := 0 to GS do begin
xv := dx * i + xt[0];
kerx := maxmin(akima_Interpolation(xv));
series1.AddXY(xv, kerx);
end;
if not mpf_is0(ixm) then begin // 虚数部0だったら虚数部グラフ無し
for i := 0 to GL + GL - 1 do yt[i] := keil[i];
akima_table;
for i := 0 to GS do begin
xv := dx * i + xt[0];
keix := maxmin(akima_Interpolation(xv));
series2.AddXY(xv, keix);
end;
end;
end;
application.ProcessMessages;
chart1coment;
EXT:
mpf_clear4(xm, vm, xvm, ixm);
mpf_clear3(nd, tmf, zz);
mpc_clear4(ri, xc, xcb, dxc);
mpf_clear3(vk, avm, tmf0);
end;
procedure TForm1.FormCreate(Sender: TObject);
var
i : integer;
N, D, tmp : mp_float;
bt : Tbitmap; // ***
begin
mpf_set_default_decprec(180); // 有効桁数180桁 50桁の精度に必要です。
setlength(BM, NB + 1); // ベルヌーイ数配列
setlength(DG, KMmax + Vmax + 2); // ディガンマ
setlength(FA, KMmax + Vmax + 1); // K1配列
setlength(PVG, KMmax + 1); // +vΓ
setlength(MVG, KMmax + 1); // -vΓ
setlength(t, GL + GL); // akima 補間値計算 配列 t
setlength(m, GL + GL + 3); // akima 補間値計算 配列 m
for i := 0 to NB do mpf_init(BM[i]);
for i := 0 to KMmax + Vmax + 1 do mpf_init(DG[i]);
for i := 0 to KMmax + Vmax do mpf_init(FA[i]);
for i := 0 to KMmax do mpf_init(PVG[i]);
for i := 0 to KMmax do mpf_init(MVG[i]);
for i := 0 to GL + GL - 1 do mpf_init(t[i]);
for i := 0 to GL + GL + 2 do mpf_init(m[i]);
mpf_init3(N, D, tmp);
mpf_init4(zero, one, two, four);
mpf_init3(three, pai, log_2pis2);
mpf_init(gamma);
mpf_read_decimal(gamma, PAnsiChar(ansistring(gstr + #00))); // γ
mpf_set0(zero);
mpf_set1(one);
mpf_set_int(two, 2);
mpf_set_int(three, 3);
mpf_set_int(four, 4);
mpf_set_pi(pai);
mpf_mul(pai, two, tmp); // 2π
mpf_ln(tmp, tmp); // ln(2π)
mpf_div(tmp, two, log_2pis2); // ln(2π)/2
Bernoulli_number_BigInteger; // ベルヌーイ数作成
for i := 0 to NB do begin
mpf_read_decimal(N, PAnsiChar(ansistring(NumeratorString[i] + #00)));
mpf_read_decimal(D, PAnsiChar(ansistring(DenominatorString[i] + #00)));
mpf_div(N, D, BM[i]);
end;
for i := 0 to KMmax + Vmax + 1 do begin
digammaMUL(i, D);
mpf_copy(D, DG[i]);
end;
for i := 0 to KMmax + Vmax do begin
factorialMul(i, N);
mpf_copy(N, FA[i]);
end;
memo1.Clear;
bt := Tbitmap.Create; // ***
bt.Width := Chart1.Width;
bt.Height := Chart1.Height;
Chart1.BackImage.Bitmap := bt;
bt.Free;
ChartBackclear; // ***
mpf_clear3(N, D, tmp);
end;
procedure TForm1.FormClose(Sender: TObject; var Action: TCloseAction);
var
i : integer;
begin
for i := 0 to NB do mpf_clear(BM[i]);
for i := 0 to KMmax + Vmax + 1 do mpf_clear(DG[i]);
for i := 0 to KMmax + Vmax do mpf_clear(FA[i]);
for i := 0 to KMmax do mpf_clear(PVG[i]);
for i := 0 to KMmax do mpf_clear(MVG[i]);
for i := 0 to GL + GL - 1 do mpf_clear(t[i]);
for i := 0 to GL + GL + 2 do mpf_clear(m[i]);
mpf_clear4(zero, one, two, four);
mpf_clear3(three, pai, log_2pis2);
mpf_clear(gamma);
end;
end.
kelvin_function_Complex_of_2nd_3rd_kind.zip
三角関数、逆三角関数、その他関数 に戻る