2024/9/27
計算範囲の拡大と若干の高速化
デバックに可成り時間を取られましたが、未だ不完全です。
超幾何関数 (Hypergeometric function)
ガウスの超幾何関数
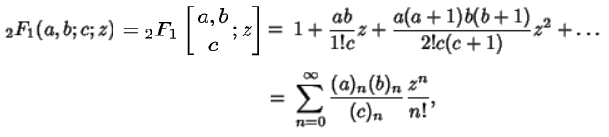
(x)n はポッホハマー記号で表した昇冪 (x)0 = 1、(x)n = x (x+1) (x+2)…(x+n−1)
値は、プログラムを組んで、n=0、n=1、n=2、と順に計算Σ値を求めて、Σ値が変化しなくなるまで計算することで、簡単に求める事が出来ます。
超幾何関数は、初期関数や特殊関数を含んでいます。
しかし、前記の超幾何関数の式では、ｚの値が１以下でないと収束しません。
cの値が負の整数であると、±∞になり、ａ或いはｂの値が負の整数であればZEROになります。
ｚの値が１を超える場合は、線形接続公式が必用です。
線形接続公式は数種類あり、zの値に応じて、適切に使用すれば、高速に計算が可能ですが、今回は二種類程度にし、変換計算を使用してみました。
a,b,cの値によって、Γ値、或いは2F1(a,b;c;z)のcの値が0又は負の整数になることがあり、正しく計算されない場合があります。
インターネットで、情報を探しても殆どの論文やレポートは、無限大になる値を避けています。
*インターネットで検索する場合、日本語ではなく、英文で検索することをお勧めします。*
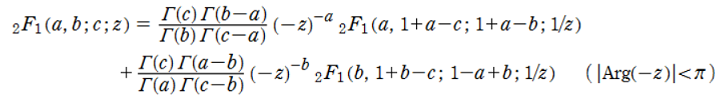
上記の線形接続公式では、Γ(x)のｘの値が0(ZERO)或いは0以下の整数であると、Γ値が±∞になり正しい値を返さないことになります。
ｔａｎ－１に関しては、正しい答えを返すことになります。
ｔａｎ－１、の時X=１の値に関しては収束しないので、計算出来ません。
又、1に近い値の場合は、収束に時間が掛かり、実際の計算に使用するのには、不向きの様です。
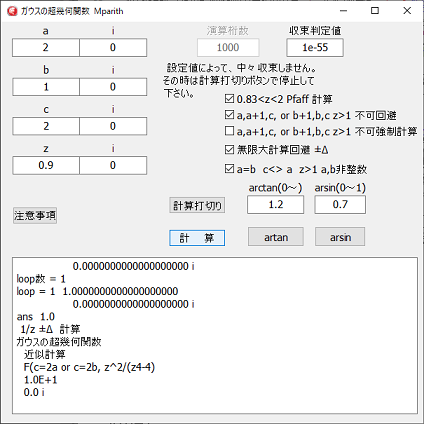一応プログラムを作成してみました。
左図の演算桁数は、演算上の有効桁数で、答えの有効桁数ではありません。
arctan。arcsinの計算時、1の値に関しては、1の値及びその近傍の値を避ける為、arctan、arcsinにそれぞれ変換して計算しています。
線形接続公式を使用する場合で、Γ値が±∞になる場合、ａ、ｂ、ｃの値を少しずらして近似値を計算していますので、正しい結果が出るとは限りませんが有効桁数25桁位はあっていると思われます。(正解の確認が取れません)
Γ値が±∞をとる場合でも、無限大では無く、出来る限り大きい値を設定して計算しているので正しく答えが出る場合もあります。
プログラム
デバッグは、不完全です注意してください。(余りにも大変なので打ち切りました。)
プログラムには、多倍長演算が組み込んであります。
組み込み方は第１種ケルビン関数を参照して下さい。
// Gaussの超幾何関数 // 値が1より小さい場合は必ず収束しますが // 1の場合は専用の計算があります、a又はbの値が負数の整数の場合は収束します。 // 1より大きい場合は、線形接続公式を計算しますが、計算は難しくなります。 // Zの値により、収束の速い線形接続公式を利用すれば良いのですが、ここでは。 // 二種類に限定しています。 // arctan(x)はxの値が1より大きくても必ず正しい値をかえします。 // Z > 1の場合Γ(x)関数を使用するのですが、xの値が0又は負の整数となると // Γ(x) +∞ or -∞となるので微小値を加減算して整数から外して計算しています。 // +Δと-Δの値を計算し平均値を答えとしています。 // |z|>1でa,b,cの値が整数の場合、或いは、虚数部が0でない場合、線形接続公式を用いても高速に計算出来ない値があります。 // 特にa=b c-a=1(c-b=1)の時は難しくなります。 unit main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons, system.UITypes, system.Math; type TForm1 = class(TForm) Memo1: TMemo; aEdit: TLabeledEdit; bEdit: TLabeledEdit; cEdit: TLabeledEdit; zEdit: TLabeledEdit; Button1: TButton; iaEdit: TLabeledEdit; ibEdit: TLabeledEdit; icEdit: TLabeledEdit; izEdit: TLabeledEdit; PrecisionEdit: TLabeledEdit; Label1: TLabel; epsEdit: TLabeledEdit; BitBtn1: TBitBtn; artanBtn: TBitBtn; ArtanedEdit: TLabeledEdit; arsinEdit: TLabeledEdit; arsinBtn: TBitBtn; CheckBox1: TCheckBox; CheckBox2: TCheckBox; CheckBox3: TCheckBox; Button2: TButton; CheckBox4: TCheckBox; CheckBox5: TCheckBox; procedure Button1Click(Sender: TObject); procedure FormCreate(Sender: TObject); procedure BitBtn1Click(Sender: TObject); procedure FormClose(Sender: TObject; var Action: TCloseAction); procedure artanBtnClick(Sender: TObject); procedure arsinBtnClick(Sender: TObject); procedure Button2Click(Sender: TObject); private { Private 宣言 } public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses mp_real, mp_cmplx, mp_types, mp_base, Velthuis.BigIntegers; const NB = 120; // ベルヌーイ数 配列数 NB + 1 var BM : array of mp_float; // ベルヌーイ数配列 NumeratorString : array[0..NB] of string; // 分子 DenominatorString : array[0..NB] of string; // Γ関数用分母 zero, one, two, three, four : mp_float; pai, maxmpf, infs : mp_float; log_2pis2 : mp_complex; // 最大公約数 ユークリッドの互除法 BigInteger function gcd_BigInteger(x, y: BigInteger): BigInteger; var t : BigInteger; begin while y <> 0 do begin t := x mod y; x := y; y := t; end; result := x; end; // ベルヌーイ数 // Akiyama-Tanigawa algorithm // BigInteger procedure Bernoulli_number_BigInteger; const n = (NB + 1) * 2; var m, j, k : integer; a : array of BigInteger; // 分子 b : array of BigInteger; // 分母 tmpN : BigInteger; // 分子 tmpD : BigInteger; // 分母 gcd : BigInteger; // 最大公約数 b0 : BigInteger; begin setlength(a, n + 1); setlength(b, n + 1); k := 0; for m := 0 to n do begin a[m] := 1; // 分子 初期値 b[m] := (m + 1); // 分母 初期値 for j := m - 1 downto 0 do begin tmpN := a[j] * b[j + 1] - a[j + 1] * b[j]; // 分子 tmpN := tmpN * (j + 1); // 〃 tmpD := b[j] * b[j + 1]; // 分母 gcd := gcd_BigInteger(tmpN, tmpD); // 最大公約数 a[j] := tmpN div gcd; b[j] := tmpD div gcd; end; if (m > 0) and (m mod 2 = 0) then begin b0 := b[0]; // logΓ関数用に分母値Bの値計算 b0 := b0 * m * (m -1); // m ベルヌーイ数No NumeratorString[k] := a[0].tostring; // 分子 DenominatorString[k] := b0.tostring; // Γ関数用分母 inc(k); end; end; end; // ログガンマ多倍長 procedure log_GammaMul(var x, ans : mp_complex); var v, w, cone, ctwo : mp_complex; tmp, tmp0, s : mp_complex; i : integer; begin mpc_init4(v, w, cone, ctwo); mpc_init3(tmp, tmp0, s); mpc_set1(cone); // 1 + 0i mpc_add(cone, cone, ctwo); // 2 + 0i mpc_set1(v); // 1 + 0i mpc_set0(tmp); // 0 + 0i mpf_set_int(tmp.re, NB); // NB + 0i while mpf_is_lt(x.re, tmp.re) do begin // while x < NB do mpc_mul(v, x, v); // v = v * x mpf_add(x.re, one, x.re); // x := x + 1 end; mpc_mul(x, x, tmp); // x^2 mpc_div(cone, tmp, w); // w = 1 / x^2 mpc_set0(s); // s = 0 + 0i for i := NB downto 1 do begin mpc_add_mpf(s, BM[i], tmp); // tmp = s + B[i] mpc_mul(tmp, w, s); // s = tmp * w end; mpc_add_mpf(s, BM[0], tmp); // tmp = s + B[0] mpc_div(tmp, x, s); // s = (s + B[0]) / x mpc_add(s, log_2pis2, s); // s = s + ln(2π)/2 mpc_ln(v, tmp); // ln(v) mpc_sub(s, tmp, s); // s := s - ln(v) mpc_sub(s, x, s); // s := s - x mpc_div(cone, ctwo, tmp); // tmp = 1/2 mpc_sub(x, tmp, tmp0); // tmp0 = x - 1/2 mpc_ln(x, tmp); // ln(x) mpc_mul(tmp0, tmp, tmp0); // tmp0 = (x - 1/2) * ln(x) mpc_add(s, tmp0, ans); // ans = s + (x - 1/2) * ln(x) mpc_clear4(v, w, cone, ctwo); mpc_clear3(tmp, tmp0, s); end; // 多倍長ガンマ 複素数 // xの値が 0 と負整数の時Γは∞になるので∞フラグセット値は1を返します。 function gammaMul(xx : mp_complex; var ans: mp_complex) : integer; label EXT; var tmp, sinx, logG, cone, cpai : mp_complex; x : mp_complex; begin mpc_init5(tmp, sinx, logG, cone, cpai); mpc_init(x); // xxの値を変化させるxxの元値を解放不可になるのでコピーして使用します // mpc_copy(xx, x); mpf_read_decimal(x.re, PAnsiChar(ansistring(string(mpf_decimal(xx.re, 200)) + #00))); mpf_read_decimal(x.im, PAnsiChar(ansistring(string(mpf_decimal(xx.im, 200)) + #00))); // 虚数部がゼロで実数部がゼロを含み負の整数だったら∞ if mpf_is0(x.im) and mpf_is_le(x.re, zero) then begin mpf_frac(x.re, tmp.re); // 実数部の小数点以下取り出し if mpf_is0(tmp.re) then begin // 小数点以下がゼロだったら mpf_copy(maxmpf, ans.re); mpf_div(x.re, two, tmp.re); mpf_frac(tmp.re, tmp.re); if not mpf_is0(tmp.re) then mpf_chs(ans.re, ans.re); // mpf_set_dbl(ans.re, maxdouble); mpf_set0(ans.im); // mpc_set0(ans); result := 1; // ∞フラグセット goto EXT; // 終了 end; end; mpc_set_mpf(cpai, pai, zero); // π+ 0i mpc_set1(cone); // 1 + 0i if mpf_is_lt(x.re, zero) then begin // x.real < 0 mpc_mul_mpf(x, pai, tmp); // x*π mpc_sin(tmp, sinx); // sin(πx); mpc_sub(cone, x, tmp); // 1-x log_GammaMul(tmp, logG); // loggamma(1-x); mpc_exp(logG, logG); // exp(loggamma) mpc_div(cpai, sinx, tmp); // π/sin(πx) mpc_div(tmp, logG, ans); // ans = π/(sin(πx) * logG(1-x)) end else begin // x.real >= 0 log_GammaMul(x, logG); // logGamma(x) mpc_exp(logG, ans); // exp(logGamma) end; result := 0; // 成功フラグ値 EXT: mpc_clear5(tmp, sinx, logG, cone, cpai); mpc_clear(x); end; // x(-0.5, 0) y(1.5, 0) 有効桁数70前後 // x(-0.5, -0.5) y(4, 0) 有効桁数60前後 // x(-0.5, 0.5) y(2, 0) 有効桁数70前後 procedure mpc_powa(x, y : mp_complex; var ans : mp_complex); var ay, ai, zero, harf, two : mp_float; begin mpf_init5(ay, ai, zero, harf, two); mpf_set_int(two, 2); // 2 mpc_pow(x, y, ans); // exp(y*ln(x)) // xの虚数部とyの虚数部0なら if mpf_is0(x.im) and mpf_is0(y.im) then begin mpf_set0(zero); // 0 mpf_inv(two, harf); // 1/2 0.5 mpf_abs(y.re, ay); // yの実数部の絶対値 mpf_frac(ay, ai); // yの実数部の絶対値の小数部 mpf_sub(ai, harf, ai); // yの実数部の絶対値の小数部と0.5の差分 // 差分がゼロ(yの実数部の小数部が0.5) if mpf_is0(ai) then // xの実数部が0と等しいか0より大きいなら if mpf_is_ge(x.re, zero) then mpf_set0(ans.im) // 答えの虚数部0 // 0より小さいなら else mpf_set0(ans.re); // 答えの実数部0 mpf_frac(y.re, ai); // 乗数の小数部 if mpf_is0(ai) then mpf_set0(ans.im); // 整数なら答えの虚数部0 end; // xの整数部とyの虚数部が0なら if mpf_is0(x.re) and mpf_is0(y.im) then begin mpf_frac(y.re, ai); // 乗数の小数部 if mpf_is0(ai) then begin // 整数なら mpf_div(y.re, two, ay); // 偶数奇数確認 mpf_frac(ay, ai); // 小数部 if mpf_is0(ai) then mpf_set0(ans.im) // 偶数なら 虚数部0 else mpf_set0(ans.re); // 奇数なら実数部0 end; end; mpf_abs(x.re, ay); mpf_abs(x.im, ai); // xの実数部と虚数部の絶対値が等しくてyがゼロでなかったら if mpf_is_eq(ay, ai) and mpf_is0(y.im) and not mpc_is0(y) then begin mpf_frac(y.re, ai); // 乗数の小数部 if mpf_is0(ai) then begin // 整数なら mpf_div(y.re, two, ay); // 偶数奇数確認 mpf_frac(ay, ai); // 小数部 if mpf_is0(ai) then begin mpf_add(two, two, two); // 4 mpf_div(y.re, two, ay); // 4偶数奇数確認 mpf_frac(ay, ai); // 小数部 if mpf_is0(ai) then mpf_set0(ans.im) // 偶数なら 虚数部0 y= 4 8 else mpf_set0(ans.re); // 偶数なら 虚数部0 y= 2 6 10 end; end; end; mpf_clear5(ay, ai, zero, harf, two); end; const NC = 10000; var BR : boolean; // 計算打切りフラグ TN : integer; // 計算実行 0 通常 1 artan 2 arsin DS : integer; // 計算表示 0 通常 1 artan 2 arsin procedure comment; var str : string; begin with form1.Memo1 do begin Clear; str := ' ガウスの超幾何関数'; lines.Append(str); str := ' zの値が1に近づくと、収束に時間が掛かります。'; lines.Append(str); str := 'その時にPfaffの変換をすると、収束が速くなるのですが、a,b,cの値に整数であると'; str := str + '正しい答えを返さない場合があります。'; lines.Append(str); str := 'zの値が0.85程度であれば、Pfaffの変換を使用しなくても、結構速く収束するので'; str := str + 'Pfaffの変換のある場合とない場合で同じ答えがでるか確認して下さい。'; lines.Append(str); str := '答えが違う場合は、その時の"a,b,c"値ではPfaffの変換は使用できません。'; lines.Append(str); str := ' 無限大回避は、"z>1"の時Γ関数を使用するのですが、Γ(x)のxの値が"0"又は'; str := str + '負の整数の時±無限大になるのを避ける為のものです。'; lines.Append(str); str := '無限大回避を使用した時と'; str := str + 'しない場合で答えが違う場合は、無限大回避を使用してください。'; lines.Append(str); str := ' Pfaff変換をした場合、計算上"z"の値が1を越え、Γ(x)の計算が使用されます。'; lines.Append(str); str := '無限大回避を使用した場合としない場合で答えが違う場合は、無限大回避を使用してください。'; lines.Append(str); end; end; // ガウスの超幾何関数 z < 1 procedure Hypergeometric_function(a, b, c, z : mp_complex; eps : mp_float; var ans : mp_complex; var n, f : integer); label EXT; var ap, bp, cp, zhn : mp_complex; ah, bh, ch, ab : mp_complex; s, sb, tmp, tmpb : mp_complex; nbig, nk : mp_float; smla, smlb, ftmp : mp_float; dpcs : integer; begin mpc_init4(ap, bp, cp, zhn); mpc_init4(ah, bh, ch, ab); mpc_init4(s, sb, tmp, tmpb); mpf_init2(nbig, nk); mpf_init3(smla, smlb, ftmp); dpcs := mpf_get_default_prec; mpc_set0(s); // 0 mpf_set0(smla); // 0 mpf_set0(smlb); // 0 mpc_copy(s, sb); mpf_set1(nk); // n! = 1 mpc_copy(z, zhn); // n = 1時値セット n=0 は1なので後で加算 mpc_copy(a, ah); // a(a+1)(a+2)(a+n-1) mpc_copy(b, bh); mpc_copy(c, ch); mpc_copy(a, ap); // a+n-1 mpc_copy(b, bp); mpc_copy(c, cp); mpf_set1(nbig); // n = 1 n := 1; // loop数 =1 mpc_set0(tmp); // 計算値初期化 0 repeat // n = 1から計算 mpc_mul(ah, bh, ab); // (a)n * (b)n if mpc_is0(ab) and not mpc_is0(ch) then begin // (a)n * (b)n = 0 ch<>0 なら f := 4; // a*b がゼロフラグセット終了 break; end; if mpc_is0(ch) then begin // (c)n = 0 なら if mpf_is_ge(s.re, zero) then f := 2 // ∞ 無限大フラグセットして終了 else f := 1; // -∞ if mpc_is0(ab) then begin f := 2; mpc_set1(ab); end; mpc_mul(ab, zhn, ans); break; end; mpc_copy(s, sb); mpc_copy(tmp, tmpb); mpc_set0(tmp); // Σ 1～ (a(n)b(n)Z^n)/(c(n)n^n) mpc_div_mpf(ab, nk, tmp); // (a)n * (b)n / n! mpc_mul(tmp, zhn, tmp); // (a)n * (b)n / n! * z^n mpc_div(tmp, ch, tmp); // (a)n * (b)n / n! * z^n / (c)n mpc_add(s, tmp, s); // Σ // form1.memo1.Lines.Append('loop = ' + intTostr(n) + string(' ' + mpf_decimal(tmp.re, 20))); mpf_add(ap.re, one, ap.re); // a = a + 1 mpf_add(bp.re, one, bp.re); // b = b + 1 mpf_add(cp.re, one, cp.re); // c = c + 1 mpc_mul(ah, ap, ah); // a(a+1)(a+2)(a+3)(a+n-1) mpc_mul(bh, bp, bh); // b(b+1)(b+2)(b+3)(b+n-1) mpc_mul(ch, cp, ch); // c(a+1)(c+2)(c+3)(c+n-1) mpc_mul(zhn, z, zhn); // z^n inc(n); // ループカウンターインクリメント mpf_add(nbig, one, nbig); // n = n + 1 mpf_mul(nk, nbig, nk); // n! mpc_abs(tmp, ftmp); if n mod 100 = 0 then begin // 指定回数に途中経過表示 form1.memo1.Lines.Append('loop = ' + intTostr(n) + string(' ' + mpf_decimal(ftmp, 20))); application.ProcessMessages; if BR then begin form1.memo1.Lines.Append('途中停止しました。'); break; end; end; // 収束判定 until (mpf_is_lt(ftmp, eps) or (n >= NC)); if (f = 1) or (f = 2) then else mpc_add_mpf(s, one, ans); // n = 0の値1を加算 form1.memo1.Lines.Append('loop数 = ' + intTostr(n)); EXT: mpc_clear4(ap, bp, cp, zhn); mpc_clear4(ah, bh, ch, ab); mpc_clear4(s, sb, tmp, tmpb); mpf_clear2(nbig, nk); mpf_clear3(smla, smlb, ftmp); end; // z > 1 a = b, c <> a // a = b c <> a 専用ルーチン procedure Hypergeometric_function_of_first_kind_aeb(a, b, c, z : mp_complex; eps : mp_float; var ans : mp_complex; var n, f : integer); label EXT; var ga, gb, gc, gcmamb, gapbmc : mp_complex; ma, amcpone, apbmcpone, cma, onema : mp_complex; onemz, cmamb, chsa, amc, onemonesz : mp_complex; cone, onmzhcab, zhma, tmc : mp_complex; cmb, gcmb, cmambpone, gcma : mp_complex; apbmc, zhamc : mp_complex; fa, fb, g1, g2: mp_complex; afa, afb : mp_complex; f1, f2 : integer; begin mpc_init5(ga, gb, gc, gcmamb, gapbmc); mpc_init5(ma, amcpone, apbmcpone, cma, onema); mpc_init5(onemz, cmamb, chsa, amc, onemonesz); mpc_init5(cone, onmzhcab, zhma, tmc, cmambpone); mpc_init5(cmb, gcmb, gcma, apbmc, zhamc); mpc_init4(fa, fb, g1, g2); mpc_init2(afa, afb); mpc_set1(cone); mpc_sub(c, a, cma); // c-a mpc_sub(cma, b, cmamb); // c-a-b mpc_sub(a, c, amc); // a-c mpc_sub(c, b, cmb); // c-b mpc_add(a, b, tmc); mpc_sub(tmc, c, apbmc); // a+b-c mpc_chs(a, chsa); // -a mpc_sub(cone, z, onemz); // 1-z mpc_add(amc, cone, amcpone); // a-c+1 mpc_add(amc, b, tmc); mpc_add(tmc, cone, apbmcpone); // a+b-c+1 mpc_sub(cone, a, onema); // 1-a mpc_sub(cma, b, tmc); mpc_add(tmc, cone, cmambpone); // c-a-b+1 mpc_inv(z, tmc); mpc_sub(cone, tmc, onemonesz); // 1-1/z gammaMul(a, ga); // Γ(a) gammaMul(b, gb); // Γ(b) gammaMul(c, gc); // Γ(c) gammaMul(cmamb, gcmamb); // Γ(c-a-b) gammaMul(cma, gcma); // Γ(c-a) gammaMul(cmb, gcmb); // Γ(c-b) gammaMul(apbmc, gapbmc); // Γ(a+b-c) mpc_powa(z, chsa, zhma); // z^-a mpc_powa(onemz, cmamb, onmzhcab); // (1-z)^(c-a-b) mpc_powa(z, amc, zhamc); // z~(a-c) mpc_mul(gc, gcmamb, g1); // Γ(c)Γ(c-a-b) mpc_mul(gcma, gcmb, tmc); // Γ(c-a)Γ(c-b) mpc_div(g1, tmc, g1); // g1 =Γ(c)Γ(c-a-b)/(Γ(c-a)Γ(c-b)) mpc_mul(gc, gapbmc, g2); // Γ(c)Γ(a+b-c) mpc_mul(ga, gb, tmc); // Γ(a)Γ(b) mpc_div(g2, tmc, g2); // g2 =Γ(c)Γ(a+b-c)/(Γ(a)Γ(b)) f1 := 0; Hypergeometric_function(a, amcpone, apbmcpone, onemonesz, eps, fa, n, f1); // 2F1(a, a-c+1, a+b-c+1, 1-1/z) f2 := 0; Hypergeometric_function(cma, onema, cmambpone, onemonesz, eps, fb, n, f2); // 2F1(c-a, 1-a, c-a-b+1, 1-1/z) mpc_mul(g1, zhma, tmc); mpc_mul(tmc, fa, afa); // A1 mpc_mul(g2, onmzhcab, tmc); mpc_mul(tmc, zhamc, tmc); mpc_mul(tmc, fb, afb); // A2 mpc_add(afa, afb, ans); // ans = A1 + A2 if f1 <> 0 then f := f1; if f2 <> 0 then f := f2; mpc_clear5(ga, gb, gc, gcmamb, gapbmc); mpc_clear5(ma, amcpone, apbmcpone, cma, onema); mpc_clear5(onemz, cmamb, chsa, amc, onemonesz); mpc_clear5(cone, onmzhcab, zhma, tmc, cmambpone); mpc_clear5(cmb, gcmb, gcma, apbmc, zhamc); mpc_clear4(fa, fb, g1, g2); mpc_clear2(afa, afb); end; // z > 1 procedure Hypergeometric_function_of_first_kind(a, b, c, amb, bma, cma, cmb, aeb, z : mp_complex; eps : mp_float; var ans : mp_complex; var n, f : integer); label EXT; var ga, gb, gc, gamb, gbma : mp_complex; gcma, gcmb, mzhma, mzhmb, mz : mp_complex; onepamc, onepbmc, onepamb, onemapb : mp_complex; ma, mb, sa, sb, tmc : mp_complex; onesz, fa, fb : mp_complex; f1, f2 : integer; begin // if mpc_is0(a) or mpc_is0(b) then begin // mpc_set1(ans); // exit; // end; mpc_init5(ga, gb, gc, gamb, gbma); mpc_init5(gcma, gcmb, mzhma, mzhmb, mz); mpc_init4(onepamc, onepbmc, onepamb, onemapb); mpc_init5(ma, mb, sa, sb, tmc); mpc_init3(onesz, fa, fb); gammaMul(a, ga); // Γ(a) gammaMul(b, gb); // Γ(b) gammaMul(c, gc); // Γ(c) gammaMul(amb, gamb); // Γ(a-b) gammaMul(bma, gbma); // Γ(b-a) gammaMul(cma, gcma); // Γ(c-a) gammaMul(cmb, gcmb); // Γ(c-b) mpc_chs(z, mz); // -z mpc_chs(a, ma); // -a mpc_chs(b, mb); // -b mpc_powa(mz, ma, mzhma); // (-z)^-a mpc_powa(mz, mb, mzhmb); // (-z)^-b mpc_set1(tmc); // mpc_sub(tmc, cma, onepamc); // 1+a-c mpc_sub(tmc, cmb, onepbmc); // 1+b-c mpc_add(tmc, amb, onepamb); // 1+a-b mpc_add(tmc, bma, onemapb); // 1-a+b mpc_inv(z, onesz); // 1/z Hypergeometric_function(a, onepamc, onepamb, onesz, eps, sa, n, f1); // 2F1(a, 1+a-c. 1+a-b, 1/z) form1.memo1.Lines.Append('loop = ' + intTostr(n) + string(' ' + mpf_decimal(sa.re, 20))); form1.memo1.Lines.Append(' ' + string(' ' + mpf_decimal(sa.im, 20)) + ' i'); // BR := false; // 割込みフラグ解除 Hypergeometric_function(b, onepbmc, onemapb, onesz, eps, sb, n, f2); // 2F1(b, 1+b-c, 1-a+b, 1/z) form1.memo1.Lines.Append('loop = ' + intTostr(n) + string(' ' + mpf_decimal(sb.re, 20))); form1.memo1.Lines.Append(' ' + string(' ' + mpf_decimal(sb.im, 20)) + ' i'); mpc_mul(gc, gbma, tmc); // Γ(c) * Γ(b-a) mpc_div(tmc, gb, tmc); // Γ(c) * Γ(b-a) / Γ(b) mpc_div(tmc, gcma, tmc); // Γ(c) * Γ(b-a) / Γ(b) / Γ(c-a) // form1.memo1.Lines.Append(' Γ1 ' + string(' ' + mpf_decimal(tmc.re, 20))); // form1.memo1.Lines.Append(' Γ1 ' + string(' ' + mpf_decimal(tmc.im, 20)) +' i'); mpc_mul(tmc, mzhma, tmc); // Γ(c) * Γ(b-a) / Γ(b) / Γ(c-a) * (-z)^-a mpc_mul(tmc, sa, fa); // Γ(c) * Γ(b-a) / Γ(b) / Γ(c-a) * (-z)^-a * 2F1(a) mpc_mul(gc, gamb, tmc); // Γ(c) * Γ(a-b) mpc_div(tmc, ga, tmc); // Γ(c) * Γ(a-b) / Γ(a) mpc_div(tmc, gcmb, tmc); // Γ(c) * Γ(a-b) / Γ(a) / Γ(c-b) // form1.memo1.Lines.Append(' Γ2 ' + string(' ' + mpf_decimal(tmc.re, 20))); // form1.memo1.Lines.Append(' Γ2 ' + string(' ' + mpf_decimal(tmc.im, 20)) +' i'); mpc_mul(tmc, mzhmb, tmc); // Γ(c) * Γ(a-b) / Γ(a) / Γ(c-b) * (-z)^-b mpc_mul(tmc, sb, fb); // Γ(c) * Γ(a-b) / Γ(a) / Γ(c-b) * (-z)^-b * 2F1(b) mpc_add(fa, fb, ans); // Σ // a = b 時は fa=fbとなり 解はfa 又は fbとなるので1/2にします if mpc_is0(aeb) then mpc_div_mpf(ans, two, ans); if (f1 = 1) or (f1 = 2) then f := 16; if (f2 = 1) or (f2 = 2) then f := 16; EXT: mpc_clear5(ga, gb, gc, gamb, gbma); mpc_clear5(gcma, gcmb, mzhma, mzhmb, mz); mpc_clear4(onepamc, onepbmc, onepamb, onemapb); mpc_clear5(ma, mb, sa, sb, tmc); mpc_clear3(onesz, fa, fb); end; // z=1 超幾何定理計算 procedure Hypergeometric_function_zeq1(a, b, c, z : mp_complex; eps : mp_float; var ans : mp_complex; var n, f : integer); label EXT; var cmamb, cma, cmb, tmp: mp_complex; gc, gcma, gcmb, gcmamb : mp_complex; begin mpc_init4(cmamb, cma, cmb, tmp); mpc_init4(gc, gcma, gcmb, gcmamb); f := 0; n := 0; mpc_sub(c, a, cmamb); // c - a mpc_sub(cmamb, b, cmamb); // c - a - b if mpf_is_le(cmamb.re, zero) then begin // Re(c-a-b) <= 0 f := 8; // ∞±符号計算フラグ mpc_set0(ans); goto EXT; end; // Re(c-a-b) > 0 時の計算 mpc_sub(c, a, cma); mpc_sub(c, b, cmb); gammaMul(c, gc); // Γ(c) gammaMul(cma, gcma); // Γ(c-a) gammaMul(cmb, gcmb); // Γ(c-b) gammaMul(cmamb, gcmamb); // Γ(c-a-b) mpc_mul(gc, gcmamb, tmp); // Γ(c) * Γ(c^a-b) mpc_div(tmp, gcma, tmp); // Γ(c) * Γ(c^a-b) / Γ(c-a) mpc_div(tmp, gcmb, ans); // Γ(c) * Γ(c^a-b) / Γ(c-a) / Γ(c-b) EXT: mpc_clear4(cmamb, cma, cmb, tmp); mpc_clear4(gc, gcma, gcmb, gcmamb); end; // arcsin計算 procedure TForm1.arsinBtnClick(Sender: TObject); var ch : integer; ars : double; tmp0, tmp1, tmp2 : mp_float; begin val(arsinEdit.Text, ars, ch); if ch <> 0 then begin application.MessageBox('arsin の値に間違いがあります。','注意',0); exit; end; if abs(ars) > 1 then begin application.MessageBox('arsin の値は±1迄にして下さい。','注意',0); exit; end; mpf_init3(tmp0, tmp1, tmp2); mpf_read_decimal(tmp0, PAnsiChar(ansistring(arsinEdit.Text + #00))); if (abs(ars) < 0.75) or (abs(ars) = 1) then TN := 2 else TN := 1; aedit.Text := '0.5'; if (abs(ars) < 0.75) or (abs(ars) = 1) then bedit.text := '0.5' else bedit.text := '1'; cedit.text := '1.5'; if (abs(ars) < 0.75) or (abs(ars) = 1) then zedit.text := arsinEdit.Text else begin mpf_mul(tmp0, tmp0, tmp1); // ars * ars mpf_sub(one, tmp1, tmp2); // 1 - ars * ars mpf_sqrt(tmp2, tmp1); // sqrt(1 - ars * ars) mpf_div(tmp0, tmp1, tmp2); // ars / sqrt(1 - ars * ars) // ars := ars / sqrt(1 - ars * ars); zedit.Text := string(mpf_decimal(tmp2, 50)); // zedit.text := floattostr(ars); end; iaedit.Text := '0'; ibedit.text := '0'; icedit.text := '0'; izedit.text := '0'; DS := 2; mpf_clear3(tmp0, tmp1, tmp2); Button1Click(nil); end; // arctan計算 procedure TForm1.artanBtnClick(Sender: TObject); var ch : integer; art : double; tmp0, tmp1, tmp2 : mp_float; begin val(ArtanedEdit.Text, art, ch); if ch <> 0 then begin application.MessageBox('artan の値に間違いがあります。','注意',0); exit; end; mpf_init3(tmp0, tmp1, tmp2); mpf_read_decimal(tmp0, PAnsiChar(ansistring(ArtanedEdit.Text + #00))); if (abs(art) < 0.75) or (abs(art) > 1.4) then TN := 1 else TN := 2; aedit.Text := '0.5'; if (abs(art) < 0.75) or (abs(art) > 1.4) then bedit.text := '1' else bedit.text := '0.5'; cedit.text := '1.5'; if (abs(art) < 0.75) or (abs(art) > 1.4) then zedit.text := artanededit.Text else begin mpf_mul(tmp0, tmp0, tmp1); // art * art mpf_add(tmp1, one, tmp2); // 1 + art * art mpf_sqrt(tmp2, tmp1); // sqrt(1 + art * art) mpf_div(tmp0, tmp1, tmp2); // art / sqrt(1 + art * art) zedit.Text := string(mpf_decimal(tmp2, 50)); end; iaedit.Text := '0'; ibedit.text := '0'; icedit.text := '0'; izedit.text := '0'; DS := 1; mpf_clear3(tmp0, tmp1, tmp2); Button1Click(nil); end; // 計算打切り procedure TForm1.BitBtn1Click(Sender: TObject); begin BR := True; end; // x <= 0 で 整数なら result = true function zeroorounder(xx: mp_complex): boolean; label EXT; var xc : mp_float; x : mp_complex; begin mpf_init(xc); mpc_init(x); // xxの値を変化させるxxの元値を解放不可になるのでコピーして使用します mpc_copy(xx, x); result := false; if not mpf_is0(x.im) then goto EXT; // frac 桁落ち対策 mpf_read_decimal(x.re, PAnsiChar(mpf_decimal(x.re, 200) + #00)); mpf_frac(x.re, xc); if not mpf_is0(xc) then goto EXT; if mpf_is_le(x.re, zero) then result := true; EXT: mpf_clear(xc); mpc_clear(x); end; // 数値の後ろのゼロ消去 function ZeroErase(s : string): string; const EP = 'E'; ZC = '0'; dt = '.'; var c : char; i, j, k, l : integer; begin l := length(s); j := 1; for i := 1 to l do begin c := s[i]; if c = EP then begin j := i - 1; break; end; j := i; end; result := ''; if j < l then begin for i := l downto j + 1 do result := s[i] + result; end; K := 1; for i := j downto 1 do begin c := s[i]; if c <> ZC then begin k := i; if c = DT then k := k + 1; break; end; end; for i := k downto 1 do result := s[i] + result; end; // 計算開始 procedure TForm1.Button1Click(Sender: TObject); label EXT, TN0E, ZG1, ZG2, ZG3; var a, b, c, z, ans : mp_complex; mz2, tans, dat, tmc : mp_complex; ch, n, pre : integer; f : integer; chd, zrd, zid : double; eps, az: mp_float; amb, bma, cma, cmb, aeb : mp_complex; d1, d2, em40 : mp_float; XLE : boolean; ap, bp, cp : mp_complex; am, bm, cm : mp_complex; zback, aback, zbackp : mp_complex; dnine, tmf, em : mp_float; absz : mp_float; df : integer; // 1E-100 以下はゼロにセット procedure zerounde1em100(var ans: mp_complex); begin mpf_read_decimal(d1, PAnsiChar(ansistring('1E-100' + #00))); mpf_abs(ans.re, tmf); if mpf_is_lt(tmf, d1) then mpf_set0(ans.re); mpf_abs(ans.im, tmf); if mpf_is_lt(tmf, d1) then mpf_set0(ans.im); end; begin val(aedit.Text, chd, ch); if ch <> 0 then begin application.MessageBox('a の値に間違いがあります。','注意',0); exit; end; val(bedit.Text, chd, ch); if ch <> 0 then begin application.MessageBox('b の値に間違いがあります。','注意',0); exit; end; val(cedit.Text, chd, ch); if ch <> 0 then begin application.MessageBox('c の値に間違いがあります。','注意',0); exit; end; val(zedit.Text, zrd, ch); if ch <> 0 then begin application.MessageBox('z の値に間違いがあります。','注意',0); exit; end; val(iaedit.Text, chd, ch); if ch <> 0 then begin application.MessageBox('a の虚数値に間違いがあります。','注意',0); exit; end; val(ibedit.Text, chd, ch); if ch <> 0 then begin application.MessageBox('b の虚数値に間違いがあります。','注意',0); exit; end; val(icedit.Text, chd, ch); if ch <> 0 then begin application.MessageBox('c の虚数値に間違いがあります。','注意',0); exit; end; val(izedit.Text, zid, ch); if ch <> 0 then begin application.MessageBox('z の虚数値に間違いがあります。','注意',0); exit; end; val(precisionedit.Text, pre, ch); if ch <> 0 then begin application.MessageBox('有効桁数 の値に間違いがあります。','注意',0); exit; end; if pre < 10 then begin application.MessageBox('有効桁数 は10以上にして下さい。','注意',0); exit; end; val(epsedit.Text, chd, ch); if ch <> 0 then begin application.MessageBox('収束判定値に間違いがあります。','注意',0); exit; end; button1.Enabled := False; BR := false; // 停止フラグリセット mpf_set_default_prec(pre); // 有効桁数セット mpc_init5(a, b, c, z, ans); mpf_init5(eps, az, tmf, em40, em); mpc_init4(mz2, tans, dat, tmc); mpc_init5(amb, bma, cma, cmb, aeb); mpf_init3(d1, d2, dnine); mpc_init4(ap, bp, cp, zbackp); mpc_init5(am, bm, cm, zback, aback); mpf_init(absz); memo1.Clear; memo1.Lines.Append('計算中'); application.ProcessMessages; mpf_read_decimal(a.re, PAnsiChar(ansistring(aedit.Text + #00))); mpf_read_decimal(b.re, PAnsiChar(ansistring(bedit.Text + #00))); mpf_read_decimal(c.re, PAnsiChar(ansistring(cedit.Text + #00))); mpf_read_decimal(z.re, PAnsiChar(ansistring(zedit.Text + #00))); mpf_read_decimal(a.im, PAnsiChar(ansistring(iaedit.Text + #00))); mpf_read_decimal(b.im, PAnsiChar(ansistring(ibedit.Text + #00))); mpf_read_decimal(c.im, PAnsiChar(ansistring(icedit.Text + #00))); mpf_read_decimal(z.im, PAnsiChar(ansistring(izedit.Text + #00))); mpf_read_decimal(eps, PAnsiChar(ansistring(epsedit.Text + #00))); mpf_read_decimal(dnine, PAnsiChar(ansistring('0.83' + #00))); mpf_read_decimal(em, PAnsiChar(ansistring('1E-30' + #00))); mpf_read_decimal(em40, PAnsiChar(ansistring('1E-35' + #00))); // 答え40桁時 ゼロ判定値 // 小数点以下入力制限 if mpf_is0(a.im) then begin mpf_frac(a.re, tmf); mpf_abs(tmf, tmf); if mpf_is_lt(tmf, em) and not mpf_is0(tmf) then ch := 80 else ch := length(string(mpf_decimal_alt(tmf, 55))); if (ch > 25) then begin application.MessageBox('a の値の小数点以下の値が長すぎます。','注意',0); goto EXT; end; end; if mpf_is0(b.im) then begin mpf_frac(b.re, tmf); mpf_abs(tmf, tmf); if mpf_is_lt(tmf, em) and not mpf_is0(tmf) then ch := 80 else ch := length(string(mpf_decimal_alt(tmf, 55))); if ch > 25 then begin application.MessageBox('b の値の小数点以下の値が長すぎます。','注意',0); goto EXT; end; end; if mpf_is0(c.im) then begin mpf_frac(c.re, tmf); mpf_abs(tmf, tmf); if mpf_is_lt(tmf, em) and not mpf_is0(tmf) then ch := 80 else ch := length(string(mpf_decimal_alt(tmf, 55))); if ch > 25 then begin application.MessageBox('c の値の小数点以下の値が長すぎます。','注意',0); goto EXT; end; end; f := 0; n := 0; // memo1.Clear; mpc_abs(z, absz); // |z| mpf_abs(z.re, az); XLE := false; mpc_set0(ans); if TN = 0 then begin // 通常計算 // z=0 Zがゼロの場合 a,b,cの値に関係なく 答えは 1 一番最初に確認 if mpc_is0(z) then begin memo1.Lines.Append('zの値がゼロです'); memo1.Lines.Append(' 1.0'); memo1.Lines.Append(' +0.0i'); goto EXT; end; // |Z| > 1 実数部0の時 if mpf_is_gt(absz, one) and mpf_is0(z.re) then begin goto ZG1; end; // 整数 (c <= 0 or a <= 0 or b <= 0) a,b,cの何れか又は全部が0を含み負の整数の場合 // zの値に関係なく通常の超幾何関数計算 Z<1の計算使用します。 二番目に確認 // /Z/の値が1より大きい場合aかb又はcがゼロになった時点で計算計算打ち切り // cが先か同時にゼロになった場合は±∞となります。 if zeroorounder(c) or (zeroorounder(a) or zeroorounder(b)) then begin memo1.Lines.Append(' (整数a<=0) or (整数b<=0) or (整数c<=0) '); Hypergeometric_function(a, b, c, z, eps, ans, n, f); goto TN0E; end; // z = 1 超幾何定理計算 複素数zの値が1の時の計算 // RE(c - a - b) > 0 の時は、超幾何定理計算 // RE(c - a - b) <= 0 の時は+∞か-∞になります // +か-かの判別は、zの値に0.7を与えて計算その時の値の符号で判定します。 if mpc_is1(z) then begin // z = 1 超幾何定理計算 Hypergeometric_function_zeq1(a, b, c, z, eps, ans, n, f); Memo1.Lines.Append(' z = 1 専用'); if f = 0 then begin Memo1.Lines.Append(' Re(c - a - b) > 0'); goto TN0E; end; // ∞符号設定 1から0.3 減算 0.7・・ 計算し∞±符号設定 if f = 8 then begin mpf_set_dbl(d1, 0.3); mpc_sub_mpf(z, d1, z); goto ZG2; end; end; // a,a+1,c or b+1,b,c /z/>1 時の近似計算設定 // aとbの差分が1の時の計算 mpf_add(a.re, one, ap.re); // 1加算 減算時桁落ち対策 mpf_add(b.re, one, bp.re); // 1加算 if mpf_is_gt(ap.re, bp.re) then begin // ap > bp なら ap <-> bp mpc_copy(ap, tmc); mpc_copy(bp, ap); mpc_copy(tmc, bp); end; mpf_sub(bp.re, ap.re, cp.re); // a,b 差分 差分は0～+ mpf_frac(a.re, tmf); // aの小数部 if checkbox4.Checked = true then begin mpf_read_decimal(cp.re, PAnsiChar(mpf_decimal(cp.re, 100) + #00)); // a,b 差分桁落ち対策 // a,b差分が1 虚数部が0 |z|>1 zの実数部が0かゼロ以上なら if mpf_is_eq(cp.re, one) and mpf_is0(ap.im) and mpf_is_gt(absz, one) and mpf_is_ge(z.re, zero) then begin if not mpf_is0(tmf) then begin // 小数部がゼロでなかったら 非整数なら if mpf_is_lt(absz, two) then begin // |z|が2より小さかったら 1 < |z| < 2 DS := 32; // 専用近似計算フラグセット 1-1/z c±Δ計算 goto ZG3; // pfaff 変換無し end else begin // |z|が2より大きかったら |z| >= 2 DS := 16; // 近似計算フラグセット 1/z a±Δ goto ZG2; // pfaff 変換不可 end; end else begin // a, b が整数なら if mpf_is_gt(absz, two) then begin // |z|が2より大きかったら /z/ > 2 DS := 16; // 近似計算 1/z a±Δ goto ZG1; // pfaff 変換可 end else begin // |z|が2より小さかったら 1 < |z| <= 2 DS := 32; // 専用近似計算フラグセット 1-1/z c±Δ計算 goto ZG3; // pfaff 変換無し end; end; end // else begin // a,b差分が1 虚数部が0 |z| >=0 Zの実数部が負数なら if mpf_is_eq(cp.re, one) and mpf_is0(ap.im) and mpf_is_ge(absz, one) and mpf_is_lt(z.re, zero) then begin DS := 8; // pfaff 変換フラグセット goto ZG1; // pfaff 変換 end; end; end; ZG3: // |a-b|=1 a,b 非整数 1-1/z 1 < |z| <= 2 c±Δ 近似計算 if (DS = 32) and not mpf_is0(z.re) then begin mpf_read_decimal(d1, PAnsiChar(ansistring('1E-40' + #00))); mpc_sub_mpf(c, d1, cp); Hypergeometric_function_of_first_kind_aeb(a, b, cp, z, eps, tmc, n, f); mpc_add_mpf(c, d1, cp); Hypergeometric_function_of_first_kind_aeb(a, b, cp, z, eps, ans, n, f); mpc_add(tmc, ans, tmc); mpc_div_mpf(tmc, two, ans); XLE := true; memo1.Lines.Append('|a-b|=1 a,b 1 < |z| <= 2'); memo1.Lines.Append('変換 1-1/z c ±Δ'); goto TN0E; end; // F a,a+1,c, z) or ( F b+1, b, c, z) z>1 の確認 幾何関数の計算はありません。 mpc_copy(a, ap); mpc_copy(b, bp); mpf_add(ap.re, one, ap.re); mpf_add(bp.re, one, bp.re); mpf_sub(bp.re, ap.re, cp.re); mpf_sub(ap.re, bp.re, am.re); mpf_read_decimal(cp.re, PAnsiChar(mpf_decimal(cp.re, 100) + #00)); // 桁落ち対策 mpf_read_decimal(am.re, PAnsiChar(mpf_decimal(am.re, 100) + #00)); // 桁落ち対策 if (mpf_is1(cp.re) or mpf_is1(am.re)) then begin if mpf_is_gt(absz, one) then begin if checkbox5.Checked = true then goto ZG1; // テスト用です 正しい答えでない場合があります memo1.Clear; memo1.Lines.Append('"a, a+1, c" or "b+1, b, c" にチェックを入れてください。'); memo1.Lines.Append('(F a,a+1, c, z) or ( F b+1, b, c, z) z > 1の条件では'); memo1.Lines.Append('演算出来ません。'); goto EXT; end; end; // F(1, 1, 2, z) z <> 1 の計算 専用 mpc_set1(tmc); // 1+0i mpc_sub(c, tmc, tmc); // c - (1+0i) if mpc_is1(a) and mpc_is1(b) and mpc_is1(tmc) and not mpc_is1(z) and not mpc_is0(z) then begin mpc_sub(tmc, z, tmc); mpc_ln(tmc, tmc); mpc_div(tmc, z, ans); mpc_chs(ans, ans); memo1.Lines.Append('F(1, 1, 2, z) z <> 1 の計算専用'); goto TN0E; end; // a = b, c / a,= 2 |z|>1 a b 非整数 // cが整数 c<=0 の場合は、先に処理されるので、aのみ近似計算 mpf_frac(a.re, ap.re); mpf_frac(b.re, bp.re); if not mpc_is0(a) and mpf_is_gt(z.re, zero) then mpc_div(c, a, cp); // c/a memo1.Lines.Append(ZeroErase(string('c/a ' + mpf_decimal(cp.re, 40)))); if mpf_is_gt(absz, one) then // z > 1 if (checkbox2.Checked = true) and not mpf_is0(ap.re) and not mpf_is0(bp.re) and mpf_is_eq(cp.re, two) and not mpc_is1(z) then begin // z範囲 1< z < 3 if mpf_is_lt(absz, three) then begin mpf_read_decimal(d1, PAnsiChar(ansistring('1E-60' + #00))); mpc_add_mpf(a, d1, ap); Hypergeometric_function_of_first_kind_aeb(ap, b, c, z, eps, tmc, n, f); mpc_sub_mpf(a, d1, am); Hypergeometric_function_of_first_kind_aeb(am, b, c, z, eps, ans, n, f); mpc_add(tmc, ans, ans); mpc_div_mpf(ans, two, ans); memo1.Lines.Append('a = b, c / a,= 2 |z|>1 a b 非整数'); memo1.Lines.Append('変換 1-1/z a ±Δ'); XLE := true; goto TN0E; end; end; // a = b, c <> a, |z| > 1 a,b z.im = 0 非整数 // Γ値に±∞無し if (checkbox2.Checked = true) and not mpf_is0(ap.re) and not mpf_is0(bp.re) and not mpf_is_eq(cp.re, two) then begin mpc_set1(tmc); // 1 mpc_add(a, b, ap); // a+b mpc_sub(ap, c, ap); // a+b-c mpc_add(ap, tmc, ap); // a+b-c+1 mpc_sub(c, a, am); // c-a mpc_sub(am, b, am); // c-a-b mpc_add(am, tmc, am); // c-a-b+1 if not zeroorounder(ap) and not zeroorounder(am) then if not zeroorounder(c) or not (zeroorounder(a) or not zeroorounder(b)) then begin mpc_sub(a, b, amb); mpc_sub(c, b, cmb); if mpc_is0(amb) and not mpc_is0(cmb) and mpf_is_gt(absz, one) and mpf_is_gt(z.re, zero) and mpf_is0(z.im) then begin Hypergeometric_function_of_first_kind_aeb(a, b, c, z, eps, ans, n, f); memo1.Lines.Append('a=b c<>a |z|>1'); memo1.Lines.Append('変換 1-1/z a ±Δ無し'); goto TN0E; end; end; end; ZG1: // Pfafの変換公式 a = b c / a = 2 c / b = 2 は計算出来ない // zの実数部がゼロの時で/z/=1ならPfafの変換使用 // |z|>=1 で a,b,cの虚数部が0でない場合はpfaff使用不可 mpf_frac(a.re, ap.re); mpf_frac(b.re, bp.re); mpf_frac(c.re, cp.re); if (mpf_is_gt(absz, dnine) and mpf_is_le(absz, one)) or ((mpf_is_gt(absz, one) and (mpf_is_lt(absz, two) and mpf_is0(ap.re) and mpf_is0(bp.re) and mpf_is0(cp.re) and (mpf_is0(a.im) and mpf_is0(b.im) and mpf_is0(c.im))))) then begin if mpf_is0(z.re) then mpf_abs(z.im, tmf); // |zim| if (checkbox3.Checked = true) or mpf_is1(tmf) then begin if not mpc_is0(a) then mpc_div(c, a, ap); if not mpc_is0(b) then mpc_div(c, b, bp); if mpf_is_eq(ap.re, two) and mpf_is_eq(bp.re, two) and mpf_is0(z.im) then else begin mpc_sub(a, b, am); mpc_sub(c, b, cp); // |z| < dnine {z| < 2 z<>1 なら Pfafの変換 if mpf_is_gt(absz, dnine) and mpf_is_lt(absz, two) and not mpc_is1(z) then begin if not (mpc_is0(am) and not (mpc_is0(am) and (mpf_is_lt(cp.re, one) or mpf_is_gt(cp.re, one)))) then begin mpc_copy(z, zbackP); DS := DS or 4; // 変換フラグセット mpc_set1(tmc); mpc_sub(z, tmc, tmc); // z - 1 mpc_div(z, tmc, z); // z = z/(z-1); mpc_abs(z, absz); // |z| mpc_sub(c, b, b); // b = c - b end; // a=b c=a+1 c=b+1 の時変換後にaにΔ値加減算 if (mpc_is0(am) and not (mpf_is_lt(cp.re, one) or mpf_is_gt(cp.re, one))) then begin mpc_copy(z, zbackP); DS := DS or 4 or 128; // 変換フラグセット mpc_set1(tmc); mpc_sub(z, tmc, tmc); // z - 1 mpc_div(z, tmc, z); // z = z/(z-1); mpc_abs(z, absz); // |z| mpc_sub(c, b, b); // b = c - b XLE := true; end; end; end; end; end else begin if mpf_is_lt(absz, two) and (mpf_is_gt(absz, one)) then begin Hypergeometric_function_of_first_kind_aeb(a, b, c, z, eps, ans, n, f); memo1.Lines.Append('1-1/z 1<|z|<2 Δ無し)'); goto TN0E; end; end; ZG2: // z > 1 // Γ値の値が±∞になる場合、微笑値Δを加減算して計算平均値を答えにしています。 // a=bの計算の時は、aのみ微笑値Δを加減算 a=bとa<>bでは、平均値の計算が違います。 if mpf_is_gt(absz, one) then begin // |z|が1より大きかったら if DS = 0 then XLE := false; mpc_sub(a, b, amb); mpc_sub(b, a, bma); mpc_sub(c, a, cma); mpc_sub(c, b, cmb); mpc_sub(a, b, aeb); // X > 1 計算で Γ値が+∞-∞になるなら近似計算 Δα値を加算減算して計算し平均値を求めます if checkbox1.Checked = true then begin if mpc_is0(amb) then mpf_read_decimal(d1, PAnsiChar(ansistring('1E-19' + #00))) else mpf_read_decimal(d1, PAnsiChar(ansistring('1E-45' + #00))); if DS and 128 = 128 then mpf_read_decimal(d1, PAnsiChar(ansistring('1.8E-29' + #00))); df := 0; // a=b a, b, if mpc_is0(amb) or (DS and 16 = 16) or (DS and 128 = 128) then begin // a=b の場合 又は DS=16 (a, b=a+1, b+1 b) df := df or 16; // aのみΔ加算減算計算 mpc_set1(aeb); // df=16時はa±Δで計算する為 aeb では無くなります end; mpc_copy(a, ap); if df and 16 = 16 then else begin if zeroorounder(amb) then df := df or 1; // x <= 0 で 整数 なら XLE = true if zeroorounder(bma) then df := df or 2; if zeroorounder(cma) then df := df or 4; if zeroorounder(cmb) then df := df or 8; end; if (df = 13) or (df = 14) then begin df := 16; mpc_set1(aeb); end; if df <> 0 then begin XLE := true; if df and 16 = 16 then begin mpc_add_mpf(a, d1, ap); mpc_sub(ap, b, amb); mpc_sub(b, ap, bma); mpc_sub(c, ap, cma); mpc_sub(c, b, cmb); end; if df and 1 = 1 then mpc_add_mpf(amb, d1, amb); if df and 2 = 2 then mpc_add_mpf(bma, d1, bma); if df and 4 = 4 then mpc_add_mpf(cma, d1, cma); if df and 8 = 8 then mpc_add_mpf(cmb, d1, cmb); Hypergeometric_function_of_first_kind(ap, b, c, amb, bma, cma, cmb, aeb, z, eps, tmc, n, f); // Δ加算計算 memo1.Lines.Append(ZeroErase(string('tmc ' + mpf_decimal(tmc.re, 40)))); mpc_sub(a, b, amb); mpc_sub(b, a, bma); mpc_sub(c, a, cma); mpc_sub(c, b, cmb); mpc_copy(a, am); if df and 16 = 16 then begin mpc_sub_mpf(a, d1, am); mpc_sub(am, b, amb); mpc_sub(b, am, bma); mpc_sub(c, am, cma); mpc_sub(c, b, cmb); end; if df and 1 = 1 then mpc_sub_mpf(amb, d1, amb); if df and 2 = 2 then mpc_sub_mpf(bma, d1, bma); if df and 4 = 4 then mpc_sub_mpf(cma, d1, cma); if df and 8 = 8 then mpc_sub_mpf(cmb, d1, cmb); Hypergeometric_function_of_first_kind(am, b, c, amb, bma, cma, cmb, aeb, z, eps, ans, n, f); // Δ減算計算 memo1.Lines.Append(ZeroErase(string('ans ' + mpf_decimal(ans.re, 42)))); mpc_add(ans, tmc, ans); mpc_div_mpf(ans, two, ans); // 平均値 if df = 16 then memo1.Lines.Append(' 1/z a ±Δ 計算') else memo1.Lines.Append(' 1/z ±Δ 計算'); end else begin Hypergeometric_function_of_first_kind(a, b, c, amb, bma, cma, cmb, aeb, z, eps, ans, n, f); // Δ=0 memo1.Lines.Append(' 1/z Δ=0 計算'); end; end else begin // 無限大回避のチェックを外すと使用されます Hypergeometric_function_of_first_kind(a, b, c, amb, bma, cma, cmb, aeb, z, eps, ans, n, f); // Δ無し Memo1.Lines.Append('1/z ±Δ無し'); end; end else if not mpc_is1(z) then begin // z < 1 通常の超幾何関数計算 Hypergeometric_function(a, b, c, z, eps, ans, n, f); Memo1.Lines.Append(' z < 1 ±Δ無し'); end; end; // TN=0 end TN0E: if TN = 1 then begin // arctan計算 mpc_mul(z, z, mz2); mpc_chs(mz2, mz2); if mpf_is_gt(absz, one) then begin // zが1より大きかったら mpc_sub(a, b, amb); mpc_sub(b, a, bma); mpc_sub(c, a, cma); mpc_sub(c, b, cmb); Hypergeometric_function_of_first_kind(a, b, c, amb, bma, cma, cmb, amb, mz2, eps, ans, n, f); end else // zが1より小さかったら Hypergeometric_function(a, b, c, mz2, eps, ans, n, f); end; if TN = 2 then begin // arcsin計算 if not mpf_is1(az) then begin mpc_mul(z, z, mz2); Hypergeometric_function(a, b, c, mz2, eps, ans, n, f); end; end; if BR then memo1.Lines.Append('計算が途中で打ち切られました、計算結果は正しくありません。'); if n >= NC then begin memo1.Lines.Append('計算が' + intTostr(NC) + 'Loopで収束しませんでした。'); memo1.Lines.Append('計算結果は正しくありません。'); end else begin if TN = 0 then begin // 通常計算 memo1.Lines.Append('ガウスの超幾何関数'); if XLE and checkbox1.Checked then memo1.Lines.Append(' 近似計算'); // memo1.Lines.Append('計算Loop数' + inttostr(n)); end; end; if (f = 1) or (f = 2) then begin // if mpf_is0(ans.re) then memo1.Lines.Append('0'); if mpf_is_ge(ans.re, zero) then memo1.Lines.Append('∞') else memo1.Lines.Append('-∞'); if mpf_is_gt(ans.im, zero) then memo1.Lines.Append('+∞i'); if mpf_is_lt(ans.im, zero) then memo1.Lines.Append('-∞i'); end; if TN = 0 then begin // 通常計算 // 絶対値が指定値より小さかったら0セット zerounde1em100(ans); // z=1 計算 ∞時 出力 if f = 8 then begin memo1.Lines.Append('z = 1'); memo1.Lines.Append(' Re(c - a - b) <= 0'); if mpf_is_ge(ans.re, zero) then memo1.Lines.Append(' ∞') else memo1.Lines.Append('-∞'); if mpf_is_gt(ans.im, zero) then memo1.Lines.Append('+∞i'); if mpf_is_lt(ans.im, zero) then memo1.Lines.Append('-∞i'); goto EXT; end; // pfaff変換時出力 if DS and 4 = 4 then begin mpc_set1(tmc); // 1 mpc_sub(tmc, zbackp, tmc); // 1-z mpc_chs(a, ap); // -a mpc_powa(tmc, ap, tmc); // (1-z)^-a mpc_mul(ans, tmc, ans); // ans = ans * ((1-z)^-a) memo1.Lines.Append(' Pfaff'); zerounde1em100(ans); end; // 二次 z^2/(z^2/(z4-4)) 変換時出力 必ずpfaffの後に実行 if (DS and 8 = 8) or (DS = 64) then begin mpc_set1(tmc); // 1 mpc_sub(tmc, zback, tmc); // 1-z mpc_chs(aback, aback); // -a mpc_div_mpf(aback, two, aback); // -a/2 mpc_powa(tmc, aback, tmc); // (1-z)^-a/2 mpc_mul(ans, tmc, ans); // ans = ans * ((1-z)^-a/2) memo1.Lines.Append(' F(c=2a or c=2b, z^2/(z4-4)'); zerounde1em100(ans); end; // 計算結果表示 近似計算時は40桁 通常は50桁表示 if f = 16 then begin memo1.Lines.Append('演算出来ません。'); end; if (f = 0) or (f = 4) then begin mpf_abs(ans.re, az); if mpf_is_gt(az, infs) then begin if mpf_is_gt(ans.re, zero) then memo1.Lines.Append(' ∞') else memo1.Lines.Append(' -∞'); end else if XLE and checkbox1.Checked then begin mpf_abs(ans.re, tmf); if mpf_is_lt(tmf, em40) then mpf_set0(ans.re); memo1.Lines.Append(ZeroErase(string(' ' + mpf_decimal(ans.re, 35)))); end else memo1.Lines.Append(ZeroErase(string(' ' + mpf_decimal(ans.re, 50)))); mpf_abs(ans.im, az); if mpf_is_gt(az, infs) then begin if mpf_is_gt(ans.im, zero) then memo1.Lines.Append(' +∞i') else memo1.Lines.Append(' -∞i'); end else begin mpf_abs(ans.re, az); if mpf_is_lt(az, infs) then if XLE and checkbox1.Checked then begin mpf_abs(ans.im, tmf); if mpf_is_lt(tmf, em40) then mpf_set0(ans.im); memo1.Lines.Append(ZeroErase(string(' ' + mpf_decimal(ans.im, 35))) + ' i'); end else memo1.Lines.Append(ZeroErase(string(' ' + mpf_decimal(ans.im, 50))) + ' i'); end; end; end; if TN = 1 then begin // arctan計算 mpc_mul(ans, z, tans); // z * if DS = 1 then memo1.Lines.Append('arctan(z) rad 超幾何関数計算'); if DS = 2 then memo1.Lines.Append('arcsin(z) rad 超幾何関数計算'); memo1.Lines.Append(ZeroErase(string(' ' + mpf_decimal(tans.re, 50)))); mpc_arctan(z, dat); memo1.Lines.Append('rad 組込み関数計算'); memo1.Lines.Append(ZeroErase(string(' ' + mpf_decimal(dat.re, 50)))); end; if TN = 2 then begin // arcsin計算 if not mpf_is1(az) then mpc_mul(ans, z, tans) // z * else begin mpf_set_pi(tans.re); mpf_div(tans.re, two, tans.re); mpc_mul(tans, z, tans) // z * end; if DS = 1 then memo1.Lines.Append('arctan(z) rad 超幾何関数計算'); if DS = 2 then memo1.Lines.Append('arcsin(z) rad 超幾何関数計算'); memo1.Lines.Append(ZeroErase(string(' ' + mpf_decimal(tans.re, 50)))); mpc_arcsin(z, dat); memo1.Lines.Append('rad 組込み関数計算'); memo1.Lines.Append(ZeroErase(string(' ' + mpf_decimal(dat.re, 50)))); end; EXT: button1.Enabled := True; TN := 0; // artn arsin 解除 DS := 0; // artn arsin 解除 mpc_clear5(a, b, c, z, ans); mpf_clear5(eps, az, tmf, em40, em); mpc_clear4(mz2, tans, dat, tmc); mpc_clear5(amb, bma, cma, cmb, aeb); mpf_clear3(d1, d2, dnine); mpc_clear4(ap, bp, cp, zbackp); mpc_clear5(am, bm, cm, zback, aback); mpf_clear(absz); end; // 初期設定 procedure TForm1.FormCreate(Sender: TObject); var i : integer; N, D, tmp : mp_float; ctmp : mp_complex; begin mpf_set_default_prec(1000); precisionedit.Text := intTostr(mpf_get_default_prec); memo1.Clear; Label1.Caption := ' 設定値によって、中々収束しません。' + #13#10 + 'その時は計算打切りボタンで停止して' + #13#10 + '下さい。'; BR := false; TN := 0; // 計算実行 0 通常 1 artan 2 arsin DS := 0; // 計算表示 0 通常 1 artan 2 arsin setlength(BM, NB + 1); // Γ関数用ベルヌーイ数配列 for i := 0 to NB do mpf_init(BM[i]); mpf_init3(N, D, tmp); mpf_init5(zero, one, two, four, three); mpf_init3(pai, maxmpf, infs); mpc_init(log_2pis2); mpc_init(ctmp); // 0,1,2,3,4, π mpf_set0(zero); mpf_set1(one); mpf_set_int(two, 2); mpf_set_int(three, 3); mpf_set_int(four, 4); mpf_set_pi(pai); // ∞設定値値 mpf_read_decimal(maxmpf, PAnsiChar(ansistring('1.0e+100000000' + #00))); // ∞判別値 mpf_read_decimal(infs, PAnsiChar(ansistring('1.0e+1000000' + #00))); // ln(2π)/2 複素数 mpc_set0(ctmp); // 0 + 0i mpf_mul(pai, two, ctmp.re); // 2π+0i mpc_ln(ctmp, ctmp); // ln(2π+0i) mpc_div_mpf(ctmp, two, log_2pis2); // ln(2π+0i)/2 // ベルヌーイ数分母分子配列表作成 Bernoulli_number_BigInteger; // 分母と分子に分かれているΓ関数用ベルヌーイ数を浮動小数点の値に変換します。 // 分母の値がΓ関数用に変換されています。 for i := 0 to NB do begin mpf_read_decimal(N, PAnsiChar(ansistring(NumeratorString[i] + #00))); mpf_read_decimal(D, PAnsiChar(ansistring(DenominatorString[i] + #00))); mpf_div(N, D, BM[i]); // BM[] Γ関数用ベルヌーイ数配列 end; comment; mpf_clear3(N, D, tmp); mpc_clear(ctmp); end; procedure TForm1.FormClose(Sender: TObject; var Action: TCloseAction); var i : integer; begin for i := 0 to NB do mpf_clear(BM[i]); mpf_clear5(zero, one, two, four, three); mpf_clear3(pai, maxmpf, infs); mpc_clear(log_2pis2); end; procedure TForm1.Button2Click(Sender: TObject); begin comment; end; end.
Hypergeometric_function.zip
三角関数、逆三角関数、その他関数 に戻る