超幾何関数の線形接続公式におけるΓ関数の取り扱い。
既に、ガウスの超幾何関数のプログラムの中で使われているのですが、改めてまとめてみました。
超幾何関数の線形接続公式に、必ずΓ値同士の計算があり、Γ値が±∞になると、計算ができなくなるのですが、除算で分母側が±∞になる場合はゼロになるので問題ないのですが、分子側だけが、無限大になる場合は演算が出来なくなります。
線形接続公式は、殆どが、二つのΓ値演算×超幾何関数2F1(z<1)の加算となります。
|z|>1でa=bの時は、二つの計算は同じ値となり、片側の値だけで答えとなります。
しかし、1/zの公式では、Γ(a-b)=Γ(0)となり、通常では計算できなくなりますが、Γ値無限大同士の除算を適用出来る場合計算できます。
この時注意すべき点は、1/zの公式の二つのΓ/Γ*2F1の計算が同じ値となります、この時の値は、片側だけの値が答えとなります。
a<>bの時は、差分とることが多く大きな値の差分となるので、長い演算桁数が必要となります。
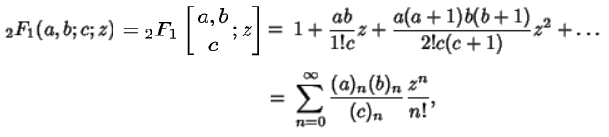
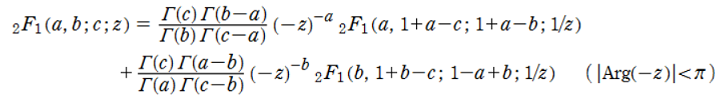
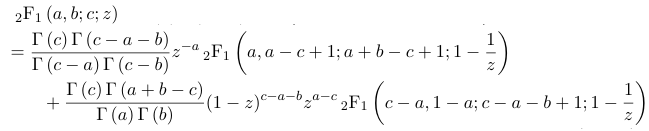
まず、
2F1(3,3,1,3;2.3;1.4)について検討します。
これを、まず1-1/zの公式で計算すると、幾何関数値にもΓ値にも無限大は発生しないので、普通に計算できます。
次に1/zの公式にあてはめて計算すると、Γ(-2)/Γ(-1)の値が発生し+∞/-∞が発生し通常の考え方では計算出来ない事になるのですが、此処で取り上げているΓの∞同士の計算を適用することで計算が出来ます。
2F1(2,3;4;-1.2)について計算します。
これを1/zの公式に適用すると、Γ値に無限大が現れるので、a±ΔのΔ値(1e-60を与えて計算すると
=0.292603862371536659067857736070593982557714489786018312384748
となります。
pfaff変換をするとz<1となり、通常の計算となり
=0.292603862371536659067857736070593982557714489786018312384748
60桁で同じ値となります。
上記計算は、偶々60桁同じ値となりましたが、条件によって、同じ値となる桁数が変わります。
しかし、少なくとも30:桁程度は、正解となります。
上記線形接続公式1/zの場合、2F1(a,1+a-c;1+a-b;1/z)
と2F1(a,1+b-c;1-a+b;1/z)の1+a-bと1-a+bがゼロでなければ、無限大を避けることができます。
そこで、aかbを僅かに変更して、ゼロからずして計算しますが、値としては大きな値となります(極限計算)。
その時は、必ず、加算されるもう一つの計算が、反対符号の大きな値となり、打ち消されて、近似値が計算されます。
Γ値に関して
次の事は、ガウスの超幾何関数にも記してあります。
Γ値にゼロはないので、±∞に注意すれば良いことになります。
分母側が、無限大になる場合は、ゼロ相当となりので問題ありませんが、分子と分母が無限大になる場合です。
例えば、
Γ(0)/Γ(-1) = -1 = 1/-(1!)
Γ(0)/Γ(-2) = 0.5 = 1/(2!)
Γ(0)/Γ(-3) = -0.166667 = 1/-(3!)
Γ(-2)/Γ(-3) = -3
= {1/(2!) ]/[1/-(3!)]
F(-3) = 1/-3 * 1/-2
* 1/-1 * 1/0
F(-2) = 1/-2 * 1/-1 * 1/0
F(-2)/Γ(-3) = (1/-2 * 1/-1 * 1/0) / (1/-3 * 1/-2 * 1/-1 * 1/0)
=
1 / (1/-3)
= -3
F(-2)×Γ(-3) = 1/-3 *
(1/-2 * 1/-1 * 1/0)2 = -∞
の様にガンマ関数に与えられた0以下の整数の階乗の逆数に従う事になります。
奇数の場合と、偶数の場合で符号の扱いに注意が必要です。
分子と分母側に同じ数の0以下の整数のガンマ関数がある場合は、階乗の計算で正しい値を求めることが出来ます。
分母の方が多い場合は、1/±∞となり限りなくゼロに近づき、分子の方が多い場合は、±∞に近づきます。
限りなく無限大に近づくと言うことから、近づいて行く途中の、適切な値を値を与えることで、正解に近い値(近似値)を求めることが出来ます。
なるべく正解に近づく様に、+Δ値と-Δ値の平均値をとって、値とします。
次のプログラムは、Γ(0)の値を分母としてΓ(x)のxの値がゼロ又は負の整数となった場合と、微少値Δを加算した場合と、減算した場合の平均値を計算した結果のプログラムを作成して、Γ値同士の除算と、±Δでの除算に問題がないことを確認したものです。
実際の、超幾何関数の計算でも確認がとれています。
参考の為にプログラムを作成してみました。
近似計算の時、50桁の精度を出す為には、Δ値は±1e-30~1e-60程度と思われますが、超幾何関数のプログラムの中では、1e-17程度のものがあります。
これは、2F1の演算速度が収束判定値が小さくなると時間がかかるので、収束判定値を1e-55程度にした時の、Δ値とした為です。
値の組み合わと、収束判定地によって変わり、収束判定地を1e-100程度にすると、Δ値は1e-40程度が良いと思われますが、演算に時間がかかります。
計算そのものは、Γ値が無限大となる場合、極限の値の計算をしていることになります。
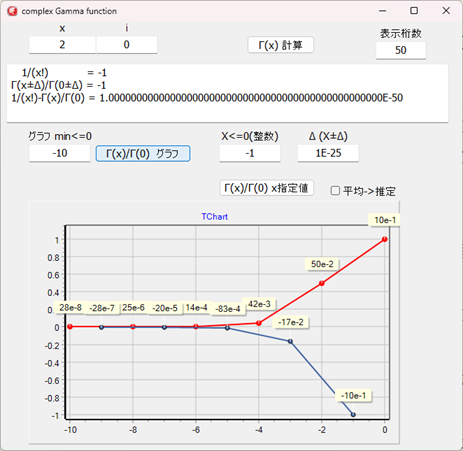 {Γ(x)
計算]ボタンは、単純にΓ(x)の値の計算です。
{Γ(x)
計算]ボタンは、単純にΓ(x)の値の計算です。
[Γ(x)/Γ(0) グラフ]ボタンは、0から指定された値までのΓ(0)を1として、前記Γ±∞の除算
Γ(x)/Γ(0) x=0~負の整数 計算グラフです。
[Γ(x)/Γ(0) x指定値]ボタン
x=0~負の整数 は、xの値と分母の0にΔ値を加減算して計算した値と、1/(x!)の値の表示、更に差分の表示をします。
差分の値が小さいほど、誤差が小さい事を表しています。
Γ値の同士の除算で値が0~負の整数の時、(1/(x!))/(1/(y!))に従うことになります。
此処での検討結果をもとに、超幾何関数 3のプログラムを修正しました。
デフォルト値の2F1の収束判定値は1e-110で、Δ値は1e-50です、これで近似計算の精度は60桁程度になります。
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls,
VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs,
VCLTee.Chart;
type
TForm1 = class(TForm)
Button1: TButton;
Memo1: TMemo;
xEdit: TLabeledEdit;
iEdit: TLabeledEdit;
Chart1: TChart;
Series1: TLineSeries;
dltEdit: TLabeledEdit;
minEdit: TLabeledEdit;
Button2: TButton;
Series2: TLineSeries;
xmEdit: TLabeledEdit;
Button3: TButton;
CheckBox1: TCheckBox;
dispEdit: TLabeledEdit;
procedure FormCreate(Sender: TObject);
procedure FormClose(Sender: TObject; var Action: TCloseAction);
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses system.Math, System.VarCmplx, Velthuis.BigIntegers,mp_real, mp_cmplx, mp_types, mp_base;
const
NB = 120; // ベルヌーイ数 配列数 NB + 1
var
BM : array of mp_float; // ベルヌーイ数配列
NumeratorString : array[0..NB] of string; // 分子
DenominatorString : array[0..NB] of string; // Γ関数用分母
zero, one, two, three, four : mp_float;
pai : mp_float;
log_2pis2 : mp_complex;
// 階乗 多倍長
procedure factorialMul(n : integer; var ans: mp_float);
label
EXT;
var
i : integer;
bi : mp_float;
begin
mpf_init(bi);
mpf_set1(ans);
mpf_copy(two, bi);
if n <= 1 then begin
goto EXT;
end;
for i := 2 to n do begin
mpf_mul(ans, bi, ans);
mpf_add(bi, one, bi);
end;
EXT:
mpf_clear(bi);
end;
// 最大公約数 ユークリッドの互除法 BigInteger
function gcd_BigInteger(x, y: BigInteger): BigInteger;
var
t : BigInteger;
begin
while y <> 0 do begin
t := x mod y;
x := y;
y := t;
end;
result := x;
end;
// ベルヌーイ数
// Akiyama-Tanigawa algorithm
// BigInteger
procedure Bernoulli_number_BigInteger;
const
n = (NB + 1) * 2;
var
m, j, k : integer;
a : array of BigInteger; // 分子
b : array of BigInteger; // 分母
tmpN : BigInteger; // 分子
tmpD : BigInteger; // 分母
gcd : BigInteger; // 最大公約数
b0 : BigInteger;
begin
setlength(a, n + 1);
setlength(b, n + 1);
k := 0;
for m := 0 to n do begin
a[m] := 1; // 分子 初期値
b[m] := (m + 1); // 分母 初期値
for j := m - 1 downto 0 do begin
tmpN := a[j] * b[j + 1] - a[j + 1] * b[j]; // 分子
tmpN := tmpN * (j + 1); // 〃
tmpD := b[j] * b[j + 1]; // 分母
gcd := gcd_BigInteger(tmpN, tmpD); // 最大公約数
a[j] := tmpN div gcd;
b[j] := tmpD div gcd;
end;
if (m > 0) and (m mod 2 = 0) then begin
b0 := b[0]; // logΓ関数用に分母値Bの値計算
b0 := b0 * m * (m -1); // m ベルヌーイ数No
NumeratorString[k] := a[0].tostring; // 分子
DenominatorString[k] := b0.tostring; // Γ関数用分母
inc(k);
end;
end;
end;
// ログガンマ多倍長
procedure log_GammaMul(var x, ans : mp_complex);
var
v, w, cone, ctwo : mp_complex;
tmp, tmp0, s : mp_complex;
i : integer;
begin
mpc_init4(v, w, cone, ctwo);
mpc_init3(tmp, tmp0, s);
mpc_set1(cone); // 1 + 0i
mpc_add(cone, cone, ctwo); // 2 + 0i
mpc_set1(v); // 1 + 0i
mpc_set0(tmp); // 0 + 0i
mpf_set_int(tmp.re, NB); // NB + 0i
while mpf_is_lt(x.re, tmp.re) do begin // while x < NB do
mpc_mul(v, x, v); // v = v * x
mpf_add(x.re, one, x.re); // x := x + 1
end;
mpc_mul(x, x, tmp); // x^2
mpc_div(cone, tmp, w); // w = 1 / x^2
mpc_set0(s); // s = 0 + 0i
for i := NB downto 1 do begin
mpc_add_mpf(s, BM[i], tmp); // tmp = s + B[i]
mpc_mul(tmp, w, s); // s = tmp * w
end;
mpc_add_mpf(s, BM[0], tmp); // tmp = s + B[0]
mpc_div(tmp, x, s); // s = (s + B[0]) / x
mpc_add(s, log_2pis2, s); // s = s + ln(2π)/2
mpc_ln(v, tmp); // ln(v)
mpc_sub(s, tmp, s); // s := s - ln(v)
mpc_sub(s, x, s); // s := s - x
mpc_div(cone, ctwo, tmp); // tmp = 1/2
mpc_sub(x, tmp, tmp0); // tmp0 = x - 1/2
mpc_ln(x, tmp); // ln(x)
mpc_mul(tmp0, tmp, tmp0); // tmp0 = (x - 1/2) * ln(x)
mpc_add(s, tmp0, ans); // ans = s + (x - 1/2) * ln(x)
mpc_clear4(v, w, cone, ctwo);
mpc_clear3(tmp, tmp0, s);
end;
// 多倍長ガンマ 複素数
// xの値が 0 と負整数の時Γは∞になるので∞フラグセット値は1を返します。
function gammaMul(xx : mp_complex; var ans: mp_complex) : integer;
label
EXT;
var
tmp, sinx, logG, cone, cpai : mp_complex;
x : mp_complex;
begin
mpc_init5(tmp, sinx, logG, cone, cpai);
mpc_init(x);
// xxの値を変化させるxxの元値を解放不可になるのでコピーして使用します
mpf_read_decimal(x.re, PAnsiChar(ansistring(string(mpf_decimal(xx.re, 200)) + #00)));
mpf_read_decimal(x.im, PAnsiChar(ansistring(string(mpf_decimal(xx.im, 200)) + #00)));
// 虚数部がゼロで実数部がゼロを含み負の整数だったら∞
if mpf_is0(x.im) and mpf_is_le(x.re, zero) then begin
mpf_frac(x.re, tmp.re); // 実数部の小数点以下取り出し
if mpf_is0(tmp.re) then begin // 小数点以下がゼロだったら
mpc_set0(ans);
result := 1; // ∞フラグセット
goto EXT; // 終了
end;
end;
mpc_set_mpf(cpai, pai, zero); // π+ 0i
mpc_set1(cone); // 1 + 0i
if mpf_is_lt(x.re, zero) then begin // x.real < 0
mpc_mul_mpf(x, pai, tmp); // x*π
mpc_sin(tmp, sinx); // sin(πx);
mpc_sub(cone, x, tmp); // 1-x
log_GammaMul(tmp, logG); // loggamma(1-x);
mpc_exp(logG, logG); // exp(loggamma)
mpc_div(cpai, sinx, tmp); // π/sin(πx)
mpc_div(tmp, logG, ans); // ans = π/(sin(πx) * logG(1-x))
end
else begin // x.real >= 0
log_GammaMul(x, logG); // logGamma(x)
mpc_exp(logG, ans); // exp(logGamma)
end;
result := 0; // 成功フラグ値
EXT:
mpc_clear5(tmp, sinx, logG, cone, cpai);
mpc_clear(x);
end;
// 複素数Γ関数計算
procedure TForm1.Button1Click(Sender: TObject);
var
ch, xi, dpcs: integer;
xd, id : double;
x, ans : mp_complex;
begin
val(xedit.Text, xd, ch);
if ch <> 0 then begin
application.MessageBox('xの値に間違いがあります。','注意',0);
exit;
end;
val(iedit.Text, id, ch);
if ch <> 0 then begin
application.MessageBox('iの値に間違いがあります。','注意',0);
exit;
end;
val(dispEdit.Text, dpcs, ch);
if ch <> 0 then begin
application.MessageBox('表示桁数 の値に間違いがあります。','注意',0);
exit;
end;
if dpcs <= 5 then begin
application.MessageBox('表示桁数 の値を大きくして下さい。','注意',0);
exit;
end;
mpc_init2(x, ans);
// 入力値をテキスト形式で読み込み多倍長数値に変換します、変換誤差防止です。
mpf_read_decimal(x.re, PAnsiChar(ansistring(xedit.Text + #00)));
mpf_read_decimal(x.im, PAnsiChar(ansistring(iedit.Text + #00)));
// Γ(x)値計算 ch=0 成功 ch=1 無限大
ch := gammaMul(x, ans);
memo1.Clear;
// 入力値表示(単なる確認用)
if id >= 0 then
memo1.Lines.Append('Γ(' + floattostr(xd) + ' +' + floatTostr(id) + 'i)') // +虚数値表示
else
memo1.Lines.Append('Γ(' + floattostr(xd) + ' ' + floatTostr(id) + 'i)'); // -虚数値表示
// 計算結果表示
if ch = 0 then begin
memo1.Lines.Append(' ' + string(mpf_decimal(ans.re, dpcs))); // 実数値表示
if mpf_is_ge(ans.im, zero) then
memo1.Lines.Append('+' + string(mpf_decimal(ans.im, dpcs)) + ' i') // +虚数値表示
else
memo1.Lines.Append( string(mpf_decimal(ans.im, dpcs)) + ' i'); // -虚数値表示
end
else begin
xi := round(xd);
if xi mod 2 <> 0 then
memo1.Lines.Append('-∞')
else
memo1.Lines.Append(' ∞'); // 無限大表示
end;
mpc_clear2(x, ans);
end;
// プログラム終了時 グローバル多倍長変数解放
procedure TForm1.Button2Click(Sender: TObject);
label
EXT;
var
dlt, x, xp, xm, mean : mp_complex;
gp, gm, meang : mp_complex;
onec, twoc : mp_complex;
mean0, ans : mp_complex;
ch, min : integer;
xd : double;
begin
val(minEdit.Text, min, ch);
if ch <> 0 then begin
application.MessageBox('min の値に間違いがあります。','注意',0);
exit;
end;
if min > 0 then begin
application.MessageBox('min の値はゼロ(0)より小さくしてください。','注意',0);
exit;
end;
val(dltEdit.Text, xd, ch);
if ch <> 0 then begin
application.MessageBox('delta の値に間違いがあります。','注意',0);
exit;
end;
if xd <= 1E-57 then begin
application.MessageBox('delta の値は1E-57より大きくしてください。','注意',0);
exit;
end;
mpc_init5(dlt, x, xp, xm, mean);
mpc_init3(gp, gm, meang);
mpc_init2(onec, twoc);
mpc_init2(mean0, ans);
mpc_set0(dlt);
mpf_read_decimal(dlt.re, PAnsiChar(ansistring(dltEdit.Text + #00)));
series1.Clear;
series2.Clear;
mpc_set1(onec); // 1
mpc_set0(x);
mpc_add(onec, onec, twoc); // 2
mpc_add(x, dlt, xp);
mpc_sub(x, dlt, xm);
gammaMul(xp, gp);
gammaMul(xm, gm);
mpc_chs(gm, gm);
mpc_add(gm, gp, mean);
mpc_div(mean, twoc, mean0); // 0の時の値
if not mpf_is0(mean0.re) then // delta値の確認
// mpc_div(mean, mean0, ans)
else begin
memo1.Lines.Append('分母がゼロになります。');
memo1.Lines.Append('delta値を大きくしてください。');
goto EXT;
end;
for ch := 0 to -min do begin
gammaMul(xp, gp);
gammaMul(xm, gm);
if ch mod 2 = 0 then mpc_chs(gm, gm)
else mpc_chs(gp, gp);
mpc_add(gm, gp, mean);
mpc_div(mean, twoc, meang);
mpc_div(meang, mean0, ans);
xd := mpf_todouble(ans.re);
// xd := 1 / xd;
if ch mod 2 = 0 then series1.AddXY(-ch, xd)
else series2.AddXY(-ch, -xd);
mpc_sub(xp, onec, xp);
mpc_sub(xm, onec, xm);
end;
EXT:
mpc_clear5(dlt, x, xp, xm, mean);
mpc_clear3(gp, gm, meang);
mpc_clear2(onec, twoc);
mpc_clear2(mean0, ans);
end;
procedure TForm1.Button3Click(Sender: TObject);
var
dlt, x, z, xp, xm, mean : mp_complex;
gp, gm, gp0, gm0, meang : mp_complex;
onec, twoc : mp_complex;
ansap, ans : mp_complex;
xmm, gmm0, gmmx, tmp : mp_complex;
ch, min, dpcs : integer;
xd : double;
begin
val(xmEdit.Text, min, ch);
if ch <> 0 then begin
application.MessageBox('min の値に間違いがあります。','注意',0);
exit;
end;
if min > 0 then begin
application.MessageBox('x の値はゼロ(0)より小さくしてください。','注意',0);
exit;
end;
val(dltEdit.Text, xd, ch);
if ch <> 0 then begin
application.MessageBox('delta の値に間違いがあります。','注意',0);
exit;
end;
if (abs(xd) > 0.1 ) then begin
application.MessageBox('delta の値0より大きくは0.1より小さくして下さい。','注意',0);
exit;
end;
val(dispEdit.Text, dpcs, ch);
if ch <> 0 then begin
application.MessageBox('表示桁数 の値に間違いがあります。','注意',0);
exit;
end;
if dpcs <= 5 then begin
application.MessageBox('表示桁数 の値を大きくして下さい。','注意',0);
exit;
end;
mpc_init5(dlt, x, xp, xm, mean);
mpc_init5(gp, gm, gp0, gm0, meang);
mpc_init3(z, onec, twoc);
mpc_init2(ansap, ans);
mpc_init4(xmm, gmm0, gmmx, tmp);
memo1.Clear;
mpc_set0(dlt);
mpf_read_decimal(dlt.re, PAnsiChar(ansistring(dltEdit.Text + #00)));
mpf_read_decimal(x.re, PAnsiChar(ansistring(xmEdit.Text + #00))); // x = xmExit
mpc_set1(onec); // 1
mpc_add(onec, onec, twoc); // 2
if min mod 2 <> 0 then ch := -1 // xが奇数なら-1
else ch := 0; // xが偶数なら 0
min := abs(min); // |x|
factorialMul(min, ansap.re) ; // x!
mpf_inv(ansap.re, ansap.re); // 1/x!
if ch <> 0 then mpc_chs(ansap, ansap); // xが奇数だったら答えの符号反転
mpc_set0(z); // x=0
mpc_add(z, dlt, xp); // 0+Δ
mpc_sub(z, dlt, xm); // 0-Δ
mpc_sub(xm, dlt, xmm); // 0-2Δ
gammaMul(xp, gp0); // Γ(0+Δ)
gammaMul(xm, gm0); // Γ(0-Δ)
gammaMul(xmm, gmm0); // Γ(0-2Δ)
mpc_add(x, dlt, xp); // x+Δ
mpc_sub(x, dlt, xm); // x-Δ
mpc_sub(xm, dlt, xmm); // x-2Δ
gammaMul(xp, gp); // Γ(x+Δ)
gammaMul(xm, gm); // Γ(x-Δ)
gammaMul(xmm, gmmx); // Γ(x-2Δ)
if checkbox1.Checked = false then begin
mpc_div(gp, gp0, tmp); // tmp = Γ(x+Δ)/Γ(0+Δ)
mpc_div(gm, gm0, ans); // ans = Γ(x-Δ)/Γ(0-Δ)
mpc_add(ans, tmp, tmp); // tmp = ans + tmp
mpc_div(tmp, twoc, ans); // ans = tmp / 2
end
else begin
mpc_div(gm, gm0, ans); // ans = Γ(x-Δ)/Γ(0-Δ)
mpc_div(gmmx, gmm0, tmp); // tmp = Γ(x-2Δ)/Γ(0-2Δ)
mpc_sub(ans, tmp, tmp); // tmp = tmp - ans
mpc_add(ans, tmp, ans); // ans = ans + tmp;
end;
mpc_sub(ansap, ans, tmp);
memo1.Lines.Append(string(' 1/(x!) = ' + mpf_decimal_alt(ansap.re, dpcs)));
memo1.Lines.Append(string('Γ(x±Δ)/Γ(0±Δ) = ' + mpf_decimal_alt(ans.re, dpcs)));
memo1.Lines.Append(string('1/(x!)-Γ(x)/Γ(0) = ' + mpf_decimal_alt(tmp.re, dpcs)));
mpc_clear5(dlt, x, xp, xm, mean);
mpc_clear5(gp, gm, gp0, gm0, meang);
mpc_clear3(z, onec, twoc);
mpc_clear2(ansap, ans);
mpc_clear4(xmm, gmm0, gmmx, tmp);
end;
// 大きなΓ値を扱う場合は有効桁数を大きくします。
procedure TForm1.FormCreate(Sender: TObject);
var
i : integer;
N, D, tmp : mp_float;
ctmp : mp_complex;
begin
mpf_set_default_decprec(500); // 有効桁数200桁 で140桁の精度に必要です。
// mpf_set_default_decprec(100); // 有効桁数100桁 で50桁の精度に必要です。
setlength(BM, NB + 1); // Γ関数用ベルヌーイ数配列
for i := 0 to NB do mpf_init(BM[i]);
mpf_init3(N, D, tmp);
mpf_init5(zero, one, two, four, three);
mpf_init(pai);
mpc_init(log_2pis2);
mpc_init(ctmp);
// 0,1,2,3,4, π
mpf_set0(zero);
mpf_set1(one);
mpf_set_int(two, 2);
mpf_set_int(three, 3);
mpf_set_int(four, 4);
mpf_set_pi(pai);
// ln(2π)/2 複素数
mpc_set0(ctmp); // 0 + 0i
mpf_mul(pai, two, ctmp.re); // 2π+0i
mpc_ln(ctmp, ctmp); // ln(2π+0i)
mpc_div_mpf(ctmp, two, log_2pis2); // ln(2π+0i)/2
// ベルヌーイ数分母分子配列表作成
Bernoulli_number_BigInteger;
// 分母と分子に分かれているΓ関数用ベルヌーイ数を浮動小数点の値に変換します。
// 分母の値がΓ関数用に変換されています。
for i := 0 to NB do begin
mpf_read_decimal(N, PAnsiChar(ansistring(NumeratorString[i] + #00)));
mpf_read_decimal(D, PAnsiChar(ansistring(DenominatorString[i] + #00)));
mpf_div(N, D, BM[i]); // BM[] Γ関数用ベルヌーイ数配列
end;
memo1.Clear;
mpf_clear3(N, D, tmp);
mpc_clear(ctmp);
end;
procedure TForm1.FormClose(Sender: TObject; var Action: TCloseAction);
var
i : integer;
begin
for i := 0 to NB do mpf_clear(BM[i]);
mpf_clear5(zero, one, two, four, three);
mpf_clear(pai);
mpc_clear(log_2pis2);
end;
end.
 Gamma_function_0f_hyp.zip
Gamma_function_0f_hyp.zip
三角関数、逆三角関数、その他関数 に戻る
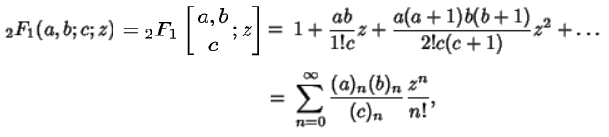
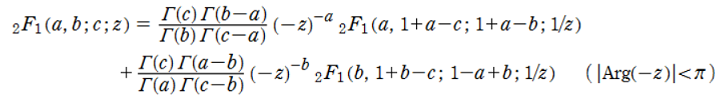
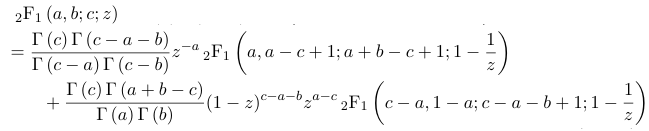
 {Γ(x)
計算]ボタンは、単純にΓ(x)の値の計算です。
{Γ(x)
計算]ボタンは、単純にΓ(x)の値の計算です。