2025/03/15
Euler 変換追加
2025/03/14
Pfaff変換の範囲変更
2025/03/10
a=b 時のz.rの最小値に間違いがあったので修正しました。
a=bにチェックを入れると収束しなくなります。
z.r > 0 -> z.r > 0.6 に変更
演算有効桁数 デフォルト 250->500 変更不可->変更可 最小100~最大2000
2025/03/08
不必要なPfaff変換をしないようにしました。
Z<1 2F1()のrepeatの高速化により最大ループ数デフォルト値を2万から10万に変更しました。
Z= 0.5 + √0.75 に対して ±0.004 の範囲外であれば収束します。
2025/03/02
Z<1演算の高速化によりpepeatルーチンの最大ループ数の変更が出来るようにしました。
2025/02/27
z<1、 2F1()のrepeatルーチンの除算と乗算の回数を減らして高速化しました。
a,a+1,c or b+1,b,c の条件 z.r >= 0を z.r>=0.7に変更
2025/02/20
F(1,2;3;z)の追加
収束しなかった時の表示変更
2025/02/14
a=b c/a=2 虚数部<>0 時のバグ修正
2025/02/12
Z<1のサブルーチンの計算手順整理
計算途中打ち切り時の計算モード変更
2025/02/04
演算精度向上の為、2F1の収束判定デフォルト値を1e-60から1e-110に変更、近似計算用Δ値を1e-17程度から1e-50に変更。
演算速度を上げる為の収束判定値1e-60でしたが、50桁の演算精度を求めるには大きすぎました、又近似計算用のΔ値は、収束判定値1e-60にたいして、出来る限り精度が上がるよう1e-17近辺の値にしていましたが、これも、極限値計算の為の値としては大きすぎました。
今回の変更で、Z>1でΓ値に無限大が現れる場合の精度が30~40桁程度から60桁程度まで上がりました。
近似計算用Δ値に対して、2F1の収束判定値は桁数で2倍以上の精度にしないと、極端に精度が悪くなります。
ガウスの超幾何関数 (Hypergeometric
function) bigdecimal version
前の超幾何関数No2の続きです。
前のプログラムでは、二種類の多倍長演算(MPArith, Bigintegr & Bigdecimal)を使用していましたが、今回は
Bigintegr & Bigdecimal に限って使用してみました。
問題は、単純な演算はあるのですが、関数演算は殆んどないことです。
複素数の演算は全く無いので、全てサブルーチンとして用意します。
主なものとして
複素数用
四則演算、log、exp、power、sin
実数用
π、tan-1、sin-1
があります、πに関しては定数として用意すれば良いのですが、今回はプログラムを用意しました。
その他、必要に応じて、単純な関数を用意しました。
問題は、log、exp、powerですが、一般的な計算を使用しているために、計算に時間がかかる事です。
主にガンマの計算に使用されるのですが、一度の計算で使用されるのは多くて八回まので、以前のプログラムに対して、計算結果が出るのに少し待ち時間が増えますが、特に気にならない程度だと思います。
前のプログラムに対して変えた条件としては、演算の有効桁数を1000桁から250桁に変更したことです。
Bigdecimalでは、除算と平方根のみ有効桁数が設定されていて、それ以外は有効桁数はなく、必要に応じて長くなります。
100桁×100桁の演算は最長200桁になります。
除算と、平方根の場合、割り切れない場合があるので、有効桁数で打ち切られます。
注意が必要なのは、乗算を繰り返すと桁数がどんどん長くなり、メモリーが不足すると同時に、演算が遅くなるので、適時、桁数指定の丸目が必要となります。
演算の有効桁数を250桁にしたことで、超幾何関数の入力値の最大値は、200程度になります、1000桁でも400程度です。
通常の超幾何関数の計算には、問題ない値でしょう。
演算の有効桁数を250にしたことで、自作の関数以外の演算速度は速くなります。
追加の超幾何関数の公式1
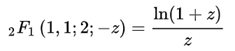
これは、超幾何関数で対数を演算するための計算式をa=1,b=1,c=2 z<>1の計算式に変換したもので、z>1の場合、通常の超幾何関数では計算できない値です。
此処のプログラムでは、上記式を使用しなくても、z>1の場合、aの値に±Δ値の計算による近似値として求めることができます。
±Δ値による計算化の値が正しいことを証明するための一部の計算としてとりいれてみました。
プログラムには、組み込んだままとしているので、確認をするためには、a,b=1 c=2 z<>1 のチェックボックスのチェックを外すだけです。
追加の超幾何関数の公式2
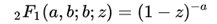 (b
arbitrary)
(b
arbitrary)
b の値は任意となっていますが、ゼロと負の整数に関しては、正しい答えを返しません。
2F1(5,-3;-3;
0.5)を上記式で計算した値と2F1(5,-3;-2.999・・・;
0.5)の値の連続性が取れないからです。
理由は簡単です
超幾何関数のbとcの値が等しいと、b/c=1となり演算の省略ができるようにみえますが、値がゼロ及び負の整数の時は、演算の途中で、bn/cn=0/0が現れるので、この時は、b/c=1として扱うことが出来ないし0/0の演算は出来ないからです。
2F1(1,b;b;z)=1F0(1;
;z)=1+z+z2+z3+z4・・・・ z<1
の等比級数もありますが、これも b の値はゼロと負の整数を除くのが条件ですね。
計算式を記号で表すと、間違いを犯す典型的な例なので、公式を利用する側の注意が必要です。
更に、Pfaff変換がありますが、これも値の条件が無いように見えますが、zの実数部が1より大きく、虚数部がゼロで、答えの虚数部がゼロでない時、虚数部の符号±が逆になるので注意が必要です。
追加の超幾何関数の公式3
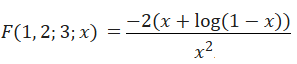 x<>1
x<>1
追加のサブルーチンとしては、a<= 0 or b<=0 or c<=0 整数の時の専用ルーチンを追加しました。
単に、計算が正しいか確認の為です。
1<zを計算するルーチンでも同じ結果が得られます。
分子がゼロでなく、分母cの値ががゼロになる場合、答えてして±∞を返すのですが、(an-1*bn-1*zn-1)/(n-1)!/cn-1*(a+n)*(b+n)/n/(c+n)
[c+n=0]で、答えを返すのか、an*bn*zn/n!/cn [cn=0]で無限大の符号が変わるのですが、此処では後者の計算を採用しています。
n!は符号には、無関係なので、最後にznを掛けるかどうかの差です。
要するに
単純に計算式道理に計算するとznを掛ける前にcnがゼロになったところで計算を打ち切るのと、分子を先に全て計算してからcnゼロで打ち切るかの差です。
(2025/02/04修正)
近似計算用のΔ値の入力が出来るようにしました。
2F1の収束判定値のデフォルトは1e-110に、近似計算用Δ値は、1e-50に設定、有効桁数50桁以上の近似計算値を得るためには、Δ値として1e-30より小さくする必要があります。
又、近似計算用Δ値に対して、2F1の収束判定値は倍以上の有効桁数の精度が必要です。
この比率が下がると、近似計算の精度が極端に下がります。
Bigintegr & Bigdecimal の組み込み方は第1種ケルビン関数を参照して下さい。
オイラー積分計算については、xy
の計算を積分分割数n×3の回数行うのですが、此処でのプログラムでは、powerの計算 xy
に時間が掛かるので、省略しました。
VarComplexの計算を利用しても良いのですが、有効桁数が少ないので誤差が大きくなります。
プログラム
プログラム上で、今回の多倍長演算で、気をつけなければならない点は、超幾何関数の公式の関数に引数を渡すとき、関数の中で引数をそのまま使用するのでなく、関数ルーチンの中で、ローカル変数を生成し、それにコピーをして計算をしたほうが、問題なく計算ができます。
特に、さらに、関数の中から、更に別の関数を呼び出す場合、引数の値が変わらない場合でも、演算の都合により、有効桁数等の変更があり値を失う事があるようです。
多倍長の変数は、doubleやsingleの変数と違い、varでない場合でも、コピーとして引き渡されるわけではないので、注意が必要です。
* c<=0 の条件以外の時は、超幾何関数のΓ値、z'<1の計算値が、±∞にならないように微少値分ずらしいるので、線形接続公式の計算の中では、無限大のフラグを無視しても良いようです。
main ルーチン
main.pas
// Gaussの超幾何関数
// 値が1より小さい場合は必ず収束しますが
// 1の場合は専用の計算があります、a又はbの値が負数の整数の場合は収束します。
// 1より大きい場合は、線形接続公式を計算しますが、計算は難しくなります。
// Zの値により、収束の速い線形接続公式を利用すれば良いのですが、ここでは。
// 三種類にしています。
// 二次変換も一部使用しています。
// arctan(x)はxの値が1より大きくても必ず正しい値をかえします。
// Z > 1の場合Γ(x)関数を使用するのですが、xの値が0又は負の整数となると
// Γ(x) +∞ or -∞となるので微小値を加減算して整数から外して計算する場合があります
// +Δと-Δの値を計算し平均値を近似値として答えとしていますが、誤差が大きくなります。
// 特にa=b c-a=1(c-b=1)の時は難しくなります。
// ガンマ値計算の分数部分で分子と分母の∞の数が等しい場合は近似計算は必要ありません。
// ガンマ計算時分子のみにガンマ値±∞がが入る場合は推定値の計算となる為、精度が低くなります。
// a, b-a+2, c=a+1, z=c z >= 2 の時 計算結果がゼロになります正しいのか疑問があります。
// z = 0.5 /z/=1 (z.im = √0.75) 時は収束しません 、近似の時も収束が遅くなりますが
// 速くする方法が分かりません。
// 2F1(5,2,4,2) = 0 + 0i
// 2F1(2,2,4,2) = -3 + 0i
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons, system.UITypes,
system.Math, Big_complex, Velthuis.BigIntegers, Velthuis.Bigdecimals;
type
TForm1 = class(TForm)
Memo1: TMemo;
aEdit: TLabeledEdit;
bEdit: TLabeledEdit;
cEdit: TLabeledEdit;
zEdit: TLabeledEdit;
Button1: TButton;
iaEdit: TLabeledEdit;
ibEdit: TLabeledEdit;
icEdit: TLabeledEdit;
izEdit: TLabeledEdit;
PrecisionEdit: TLabeledEdit;
Label1: TLabel;
epsEdit: TLabeledEdit;
BitBtn1: TBitBtn;
artanBtn: TBitBtn;
ArtanedEdit: TLabeledEdit;
arsinEdit: TLabeledEdit;
arsinBtn: TBitBtn;
CheckBox1: TCheckBox;
CheckBox2: TCheckBox;
CheckBox3: TCheckBox;
Button2: TButton;
CheckBox4: TCheckBox;
CheckBox5: TCheckBox;
CheckBox6: TCheckBox;
Label2: TLabel;
CheckBox7: TCheckBox;
CheckBox9: TCheckBox;
deltbox: TCheckBox;
deltEdit: TEdit;
CheckBox8: TCheckBox;
CheckBox10: TCheckBox;
MaxLoopEdit: TLabeledEdit;
Label3: TLabel;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
procedure artanBtnClick(Sender: TObject);
procedure arsinBtnClick(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure FormCloseQuery(Sender: TObject; var CanClose: Boolean);
procedure epsEditChange(Sender: TObject);
private
{ Private 宣言 }
function inputcheck(var pre: integer): boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
paib : bigdecimal;
z10 : cbig;
Z10F : boolean = false;
const
DPS = 300; // bigdecimal 有効桁数 入力値 ±200が限度
// DPS = 1000; // bigdecimal 有効桁数 入力値 ±400が限度
implementation
{$R *.dfm}
const
NB = 120; // ベルヌーイ数 配列数 NB + 1
EPSC = '1e-150';
var
BM : array[0..NB] of Bigdecimal; // ベルヌーイ数配列
log_2pis2 : cbig;
maxmpfbig : Bigdecimal;
zero, one, two, three, four : bigdecimal;
infs : bigdecimal;
// 最大公約数 ユークリッドの互除法 BigInteger
function gcd_BigInteger(x, y: BigInteger): BigInteger;
var
t : BigInteger;
begin
while y <> 0 do begin
t := x mod y;
x := y;
y := t;
end;
result := x;
end;
// ベルヌーイ数
// Akiyama-Tanigawa algorithm
// BigInteger
procedure Bernoulli_number_BigInteger;
const
n = (NB + 1) * 2;
var
m, j, k, dpcs: integer;
a : array of BigInteger; // 分子
b : array of BigInteger; // 分母
tmpN : BigInteger; // 分子
tmpD : BigInteger; // 分母
gcd : BigInteger; // 最大公約数
b0 : BigInteger;
ad, bd : bigdecimal;
ctwo, tmpb : cbig;
epsb : bigdecimal;
begin
dpcs := BigDecimal.DefaultPrecision;
epsb := EPSC;
paib := pi_big;
ctwo.r := bigdecimal.Two;
ctwo.i := bigdecimal.Zero; // 2 + 0i
tmpb.r := paib + paib; // 2pi
tmpb.i := bigdecimal.Zero;;
log_2pis2 := log_big(tmpb, epsb, dpcs);
// 除算前桁合わせ
log_2pis2.r := log_2pis2.r.RoundToPrecision(dpcs); // dpcs桁に丸め
log_2pis2.i := log_2pis2.i.RoundToPrecision(dpcs); // dpcs桁に丸め
log_2pis2 := cdiv(log_2pis2, ctwo);
setlength(a, n + 1);
setlength(b, n + 1);
k := 0;
for m := 0 to n do begin
a[m] := 1; // 分子 初期値
b[m] := (m + 1); // 分母 初期値
for j := m - 1 downto 0 do begin
tmpN := a[j] * b[j + 1] - a[j + 1] * b[j]; // 分子
tmpN := tmpN * (j + 1); // 〃
tmpD := b[j] * b[j + 1]; // 分母
gcd := gcd_BigInteger(tmpN, tmpD); // 最大公約数
a[j] := tmpN div gcd;
b[j] := tmpD div gcd;
end;
ad := a[0];
ad := ad.RoundToPrecision(dpcs); // dpcs桁に丸め
if (m > 0) and (m mod 2 = 0) then begin
b0 := b[0]; // logΓ関数用に分母値Bの値計算
b0 := b0 * m * (m -1); // m ベルヌーイ数No
bd := b0;
bd := bd.RoundToPrecision(dpcs); // dpcs桁に丸め
BM[k] := ad / bd;
inc(k);
end;
end;
end;
// ログガンマ多倍長
procedure log_GammaMul(x: cbig; var ans : cbig);
var
xx, v, w, cone, ctwo : cbig;
tmp, tmp0, s, cans : cbig;
i, dpcs : integer;
epsb : bigdecimal;
begin
dpcs := BigDecimal.DefaultPrecision;
epsb := EPSC;
xx := x;
cone.r := bigdecimal.One;
cone.i := bigdecimal.Zero; // 1 + 0i
ctwo := cadd(cone, cone); // 2 + 0i
v := cone; // 1 + 0i
tmp.i := bigdecimal.Zero; // 0 + 0i
tmp.r := NB; // NB + 0i
while xx.r < tmp.r do begin
v := cmul(v, xx); // v = v * x
// 繰り返し計算による桁憎防止
v := cbiground(v, dpcs);
xx := cadd(xx, cone); // x := x + 1
end;
tmp := cmul(xx, xx); // x^2
w := cdiv(cone, tmp); // w = 1 / x^2
s := cbiground(s, dpcs);
tmp.i := bigdecimal.Zero;
for i := NB downto 1 do begin
tmp.r := s.r + BM[i]; // tmp = s + B[i]
tmp.i := s.i;
s := cmul(tmp, w); // s = tmp * w
// 繰り返し計算による桁憎防止
s := cbiground(s, dpcs);
end;
tmp.r := s.r + BM[0]; // tmp = s + B[0]
tmp.i := s.i;
s := cdiv(tmp, xx); // s = (s + B[0]) / x
s := cadd(s, log_2pis2); // s = s + ln(2π)/2
tmp := log_big(v, epsb, dpcs); // ln(v)
s := csub(s, tmp); // s := s - ln(v)
s := csub(s, xx); // s := s - x
tmp := cdiv(cone, ctwo); // tmp = 1/2
tmp0 := csub(xx, tmp); // tmp0 = x - 1/2
tmp := log_big(xx, epsb, dpcs); // ln(x)
tmp0 := cmul(tmp0, tmp); // tmp0 = (x - 1/2) * ln(x)
cans := cadd(s, tmp0); // ans = s + (x - 1/2) * ln(x)
// 解答桁合わせ
cans := cbiground(cans, dpcs);
ans := cans;
end;
// 多倍長ガンマ 複素数
// xの値が 0 と負整数の時Γは∞になるので∞フラグセット値は1を返します。
function gammabig(xx : cbig; var ans: cbig) : integer;
var
tmp, sinx, logG, cone, cpai : cbig;
x : cbig;
czero, cans : cbig;
btwo, eps : bigdecimal;
dpcs : integer;
begin
dpcs := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ
czero.r := bigdecimal.Zero;
czero.i := bigdecimal.Zero;
cone.r := bigdecimal.one;
cone.i := bigdecimal.zero;
btwo := bigdecimal.Two;
eps := '1e-200';
// xxの値を変化させるxxの元値を解放不可になるのでコピーして使用します
x := xx;
// 虚数部がゼロで実数部がゼロを含み負の整数だったら∞
if (x.i = czero.i) and (x.r <= czero.r) then begin
tmp.r := x.r.Frac; // 実数部の小数点以下取り出し
if tmp.r = czero.r then begin // 小数点以下がゼロだったら
ans.r := maxmpfbig;
tmp.r := x.r / btwo;
tmp.r := tmp.r.Frac;
if tmp.r <> czero.r then ans.r := -ans.r; // 奇数だったら符号反転
ans.i := czero.i;
result := 1; // ∞フラグセット
exit; // 終了
end;
end;
cpai.r := paib;
cpai.i := czero.i; // π+ 0i
// 除算時用桁合わせ
cbiground(cpai, dpcs);
if x.r < czero.r then begin // x.real < 0
tmp := cmul(x, cpai); // x*π
tmp := cbiground(tmp, dpcs);
sinx := sin_big(tmp, eps, dpcs); // sin(πx);
tmp := csub(cone, x); // 1-x
log_GammaMul(tmp, LogG); // loggamma(1-x);
logG := exp_big(logG, dpcs, eps); // exp(loggamma)
cpai := cbiground(cpai, dpcs);
sinx := cbiground(sinx, dpcs);
tmp := cdiv(cpai, sinx); // π/sin(πx)
logG := cbiground(logG, dpcs);
tmp := cbiground(tmp, dpcs);
cans := cdiv(tmp, logG);
end
else begin // x.real >= 0
log_GammaMul(x, logG); // logGamma(x)
cans := exp_big(logG, dpcs, eps); // exp(loggamma)
end;
ans := cbiground(cans, dpcs);
result := 0; // 成功フラグ値
end;
const
NC = 100000;
var
BR, BRB : boolean; // 計算打切りフラグ
NBack : integer; // 打ち切り時n数
TN : integer; // 計算実行 0 通常 1 artan 2 arsin
DS : integer; // 計算表示 0 通常 1 artan 2 arsin
epsback : bigdecimal;
maxloops, disploops : integer; // z<1 2F1 ループ数
procedure comment;
var
str : string;
begin
with form1.Memo1 do begin
Clear;
str := ' ガウスの超幾何関数';
lines.Append(str);
str := ' |z|の値が1に近づくと、収束に時間が掛かります。';
lines.Append(str);
str := 'その時にPfaffの変換をすると、収束が速くなるのですが、a,b,cの値に整数であると';
str := str + '近似値計算となる場合があります。';
lines.Append(str);
str := 'zの値が0.85程度であれば、Pfaffの変換を使用しなくても、結構速く収束するので';
str := str + 'Pfaffの変換のある場合とない場合で同じ答えがでるか確認して下さい。';
lines.Append(str);
str := '答えが違う場合は、その時の"a,b,c"値ではPfaffの変換は使用できません。';
lines.Append(str);
str := ' 無限大回避は、"|z|>1"の時Γ関数を使用するのですが、Γ(x)のxの値が"0"又は';
str := str + '負の整数の時±無限大になるのを避ける為のものです。';
lines.Append(str);
str := '無限大回避を使用した時と';
str := str + 'しない場合で答えが違う場合は、無限大回避を使用してください。';
lines.Append(str);
str := ' Pfaff変換をした場合、計算上"|z|"の値が1を越え、Γ(x)の計算が使用されます。';
lines.Append(str);
str := '無限大回避を使用した場合としない場合で答えが違う場合は、無限大回避を使用してください。';
lines.Append(str);
end;
end;
// a,b <= 0 c <= 0 整数 計算
procedure Hypergeometric_functionbig_zero(a, b, c, z : cbig; eps : bigdecimal; var ans : cbig; var n, f : integer);
var
abig, bbig, ccbig, zbig : cbig;
ap, bp, cp, zhn : cbig;
ah, bh, ch : cbig;
s, tmp, zerobig : cbig;
np, nh : bigdecimal;
dpcs : integer;
begin
dpcs := BigDecimal.DefaultPrecision;
abig := a;
bbig := b;
ccbig := c;
zbig := z;
zerobig.r := bigdecimal.Zero;
zerobig.i := bigdecimal.Zero;
s := zerobig; // s= 0
ah := abig;
bh := bbig;
ch := ccbig;
ap := abig;
bp := bbig;
cp := ccbig;
np := one;
nh := one;
zhn := zbig;
n := 1;
while not aeqb(ah, zerobig) and not aeqb(bh, zerobig) and not aeqb(ch, zerobig) do begin
tmp := cmul(cmul(ah, bh), zhn); // an*bh*z^n
tmp := cbiground(tmp, dpcs);
ch := cbiground(ch, dpcs);
tmp := cdiv(tmp, ch); // an*bh*z^n / ch
nh := nh.RoundToPrecision(dpcs);
tmp := cdivb(tmp, nh); // an*bh*z^n / ch / n!
s := cadd(s, tmp); // Σan*bh*z^n / ch / n!
ap.r := ap.r + one; // a = a + 1
bp.r := bp.r + one; // b = b + 1
cp.r := cp.r + one; // c = c + 1
np := np + one; // n = n + 1
ah := cmul(ah, ap); // ah=a(a+1)(a+2)(a+n-1)
bh := cmul(bh, bp); // bh=b(b+1)(b+2)(b+n-1
ch := cmul(ch, cp); // ch=c(c+1)(c+2)(c+n-1
nh := nh * np; // n!
zhn := cmul(zhn, zbig); // z^n
inc(n);
end;
tmpb := cmul(cmul(ah, bh), zhn); // ah * bh * z^n
if aeqb(tmpb, zerobig) then begin // ah * bh * z^n = 0
s.r := s.r + one; // s = s + 1
ans := s; // ans = s
f := 0;
end;
if aeqb(ch, zerobig) then begin // ch = 0
tmpb := cmul(cmul(ap, bp), zbig); // ap * bp * zhn
tmp := cmul(tmpb, tmp); // tmp * ap * bp * zhn
if tmp.i > zero then f := 1;
if tmp.r > zero then f := 1;
if tmp.i < zero then f := -1;
if tmp.r < zero then f := -1;
if not aeqb(tmp, zerobig) then ans := tmp;
end;
end;
// ガウスの超幾何関数 z < 1
procedure Hypergeometric_functionbig(a, b, c, z : cbig; eps : bigdecimal; var ans : cbig; var n, f : integer);
const
MODN = 100; // MODN に一回表示
F8DN = 310; // f=8 z=1 無限大時符号確認 abc入力値より大きい値に設定
var
ap, bp, cp : cbig;
ab : cbig;
s, alpha, cn : cbig;
nbig, ptmp : bigdecimal;
ftmp, oneb, epsbig : bigdecimal;
dpcs, NN, NM, nd : integer;
zbig, ansbig : cbig;
begin
NN := maxloops; // 最大ループ数の設定
if BRB then NN := NBack; // 打ち切り回数設定なら 打ち切りの時の値に設定
if BR then begin // 前の計算時計算打ち切りがあったら
NN := NBack; // 打ち切りの時の値に設定
BR := false; // 打ち切りフラグ解除
BRB := true; // 以後の計算は打ち切りの時の値に設定に
end;
NM := MODN;
if f = 8 then begin // z=1 無限大時符号確認用
NN := F8DN;
NM := NN + 1;
end;
dpcs := BigDecimal.DefaultPrecision;
zbig := z;
epsbig := eps;
oneb := bigdecimal.One;
s.r := zero; // s= 0
s.i := zero;
ap := a; // a
bp := b; // b
cp := c; // c
nbig := oneb; // 1
n := 1; // loop数 =1
nd := 1; // 表示用カウンタ =1
tmp.r := one; // 初期値1
tmp.i := zero;
repeat // n = 1から計算
ab := cmul(cmul(ap, bp), zhn); // '(a)n * '(b)n * z^n
cn := cmulb(cp, nbig); // '(c)n * n
ab := cbiground(ab, dpcs); // dpcs桁に丸め
cn := cbiground(cn, dpcs); // dpcs桁に丸め
alpha := cmul(cdiv(ab, cn), alpha); // (a)n * (b)n * z^n / ((c)n * n1)
s := cadd(s, alpha); // Σ
ap.r := ap.r + oneb; // a = a + 1
bp.r := bp.r + oneb; // b = b + 1
cp.r := cp.r + oneb; // c = c + 1
nbig := nbig + oneb; // n = n + 1
inc(n); // ループカウンターインクリメント
ftmp := cabs(alpha, dpcs);
if n = disploops then begin // 指定回数に途中経過表示
ptmp := ftmp;
ptmp := ptmp.RoundToPrecision(20);
form1.memo1.Lines.Append('loop = ' + intTostr(n) + ' ' + ptmp.ToString);
application.ProcessMessages;
if BR then begin
NBack := n;
form1.memo1.Lines.Append('途中停止しました。');
break;
end;
end;
// 収束判定
until (ftmp < epsbig) or (n >= NN);
if f = 8 then ansbig := s // f= 8 z=1 ∞符号確認用
else begin
ansbig.r := s.r + oneb; // n = 0の値1を加算
ansbig.i := s.i;
end;
ans := cbiground(ansbig, dpcs); // dpcs桁に丸め
if ftmp < epsback then epsback := ftmp; // epsback 表示桁数設定用
alpha := cbiground(ansbig, 15);
if f <> 8 then
form1.memo1.Lines.Append('z<1 loop数 = ' + intTostr(n) + ' ' + alpha.r.ToString + ' ' + alpha.i.ToString + ' i');
end;
// z > 1 a = b, c <> a
// a = b c <> a 専用ルーチン
procedure Hypergeometric_function_of_first_kind_aeb(a, b, c, z : cbig; eps : bigdecimal; var ans : cbig; var n, f : integer);
const
LNEPS = '1e-100';
var
ga, gb, gc, gcmamb, gapbmc : cbig;
amcpone, apbmcpone, cma, onema : cbig;
onemz, cmamb, chsa, amc, onemonesz : cbig;
cone, onmzhcab, zhma, tmc : cbig;
cmb, gcmb, cmambpone, gcma : cbig;
apbmc, zhamc : cbig;
fa, fb, g1, g2: cbig;
afa, afb : cbig;
f1, f2, dpcs : integer;
abig, bbig, ccbig, zbig, ansbig : cbig;
epsbig, epsln : Bigdecimal;
n1, n2 : integer;
begin
dpcs := BigDecimal.DefaultPrecision;
epsln := LNEPS;
abig := a;
bbig := b;
ccbig := c;
zbig := z;
epsbig := eps;
cone.r := bigdecimal.One;
cone.i := bigdecimal.Zero;
cma := csub(ccbig, abig); // c-a
cmamb := csub(cma, bbig); // c-a-b
amc := csub(abig, ccbig); // a-c
cmb := csub(ccbig, bbig); // c-b
tmc := cadd(abig, bbig);
apbmc := csub(tmc, ccbig); // a+b-c
chsa := cchs(abig);
onemz := csub(cone, zbig); // 1-z
amcpone := cadd(amc, cone); // a-c+1
tmc := cadd(amc, bbig); // a+b-c
apbmcpone := cadd(tmc, cone); // a+b-c+1
onema := csub(cone, abig); // 1-a
tmc := csub(cma, bbig); // c-a-b
cmambpone := cadd(tmc, cone); // c-a-b+1
tmc := cdiv(cone, zbig); // 1/z
onemonesz := csub(cone, tmc); // 1-1/z
gammabig(abig, ga); // Γ(a)
gammabig(bbig, gb); // Γ(b)
gammabig(ccbig, gc); // Γ(c)
gammabig(cmamb, gcmamb); // Γ(c-a-b)
gammabig(cma, gcma); // Γ(c-a)
gammabig(cmb, gcmb); // Γ(c-b)
gammabig(apbmc, gapbmc); // Γ(a+b-c)
zhma := pow_big(zbig, chsa, epsln); // z^-a
onmzhcab := pow_big(onemz, cmamb, epsln); // (1-z)^(c-a-b)
zhamc := pow_big(zbig, amc, epsln); // z~(a-c)
g1 := cmul(gc, gcmamb); // Γ(c)Γ(c-a-b)
tmc := cmul(gcma, gcmb); // Γ(c-a)Γ(c-b)
g1 := cbiground(g1, dpcs); // dpcs桁に丸め
tmc := cbiground(tmc, dpcs); // dpcs桁に丸め
g1 := cdiv(g1, tmc); // g1 =Γ(c)Γ(c-a-b)/(Γ(c-a)Γ(c-b))
g2 := cmul(gc, gapbmc); // Γ(c)Γ(a+b-c)
tmc := cmul(ga, gb); // Γ(a)Γ(b)
g2 := cbiground(g2, dpcs); // dpcs桁に丸め
tmc := cbiground(tmc, dpcs); // dpcs桁に丸め
g2 := cdiv(g2, tmc); // g2 =Γ(c)Γ(a+b-c)/(Γ(a)Γ(b))
f1 := 0;
Hypergeometric_functionbig(abig, amcpone, apbmcpone, onemonesz, epsbig, fa, n1, f1); // 2F1(a, a-c+1, a+b-c+1, 1-1/z)
// tmc := cbiground(fa, 40);
// form1.memo1.Lines.Append('loop = ' + intTostr(n) + ' fa ' + tmc.r.ToString);
// form1.memo1.Lines.Append(' ' + 'fai ' + tmc.i.ToString + ' i');
f2 := 0;
Hypergeometric_functionbig(cma, onema, cmambpone, onemonesz, epsbig, fb, n2, f2); // 2F1(c-a, 1-a, c-a-b+1, 1-1/z)
// tmc := cbiground(fb, 40);
// form1.memo1.Lines.Append('loop = ' + intTostr(n) + ' fb ' + tmc.r.ToString);
// form1.memo1.Lines.Append(' ' + 'fbi ' + tmc.i.ToString + ' i');
tmc := cmul(g1, zhma);
afa := cmul(tmc, fa); // A1
tmc := cmul(g2, onmzhcab);
tmc := cmul(tmc, zhamc);
afb := cmul(tmc, fb); // A2
ansbig := cadd(afa, afb); // ans = A1 + A2
// tmc := cbiground(onmzhcab, 40);
// form1.memo1.Lines.Append(' onmzhcab ' + tmc.r.ToString);
// tmc := cbiground(ansbig, 40);
// form1.memo1.Lines.Append(' ans ' + tmc.r.ToString);
if f1 <> 0 then f := f1;
if f2 <> 0 then f := f2;
if n1 >= n2 then n := n1
else n := n2;
ans := cbiground(ansbig, dpcs); // dpcs桁桁に丸め
end;
// x <= 0 で 整数なら result = true
function zeroorounderbig(xx: cbig): boolean;
var
xc : bigdecimal;
x : cbig;
begin
// xxの値を変化させるxxの元値を解放不可になるのでコピーして使用します
x := xx;
result := false;
if not x.i.IsZero then exit;
// frac 桁落ち対策
x.r := x.r.RoundToPrecision(200);
xc := x.r.Frac;
if not xc.IsZero then exit;;
if x.r.IsNegative or x.r.IsZero then result := true;
end;
// +∞ = +1;
// -∞ = -1;
// 整数 <=0 奇数 -1 偶数 +1
function infpmbig(x: bigdecimal): integer;
var
tmp, two , xx, fra: bigdecimal;
dpcs : integer;
begin
result := 0;
dpcs := BigDecimal.DefaultPrecision;
xx := x;
two := bigdecimal.Two;
xx := xx.RoundToPrecision(dpcs);
two := two.RoundToPrecision(dpcs);
tmp := xx / two;
fra := tmp.Frac;
if fra.IsZero then result := 1
else result := -1;
end;
// 階乗 多倍長
procedure factorialMulbig(n : integer; var ans : bigdecimal);
var
i : integer;
bi, one, ians: biginteger;
begin
one := biginteger.One;
ans := one; // 0!, 1!
if n <= 1 then exit;
ians := one;
bi := one + one; // 2~
for i := 2 to n do begin // n!
ians := ians * bi;
bi := bi + one;
end;
ans := ians;
end;
// {Γ(a)Γ(b)}/{Γ(a)Γ(a)}
function gammaCalcbig(a, b, c, d: cbig; var ans: cbig): integer;
var
af, bf, cf, df : integer;
ac, bc, cc, dc, oneb : cbig;
dlt : bigdecimal;
dpcs : integer;
procedure gmmadlt(var x, g : cbig);
var
n : integer;
dn : double;
begin
dn := x.r.AsDouble;
n := round(dn);
n := abs(n);
g.i := bigdecimal.Zero;
factorialMulbig(n, g.r);
oneb := cbiground(oneb, dpcs);
g := cbiground(g, dpcs);
g := cdiv(oneb, g);
if n mod 2 <> 0 then begin
g.r := -g.r;
g.i := -g.i
end;
end;
begin
dpcs := BigDecimal.DefaultPrecision;
oneb.r := bigdecimal.One;
oneb.i := bigdecimal.Zero;
result := 1;
ans.r := bigdecimal.Zero;
ans.i := bigdecimal.Zero;
af := 0;
bf := 0;
cf := 0;
df := 0;
dlt := '1E-55';
if zeroorounderbig(a) then af := infpmbig(a.r);
if zeroorounderbig(b) then bf := infpmbig(b.r);
if zeroorounderbig(c) then cf := infpmbig(c.r);
if zeroorounderbig(d) then df := infpmbig(d.r);
if af <> 0 then gmmadlt(a, ac) // Γ(a)
else gammabig(a, ac);
if bf <> 0 then gmmadlt(b, bc) // Γ(b)
else gammabig(b, bc);
if cf <> 0 then gmmadlt(c, cc) // Γ(c)
else gammabig(c, cc);
if df <> 0 then gmmadlt(d, dc) // Γ(d)
else gammabig(d, dc);
if (abs(af) + abs(bf)) = (abs(cf) + abs(df)) then begin
ans := cmul(ac, bc); // Γ(a) * Γ(b)
ans := cbiground(ans, dpcs);
cc := cbiground(cc, dpcs);
ans := cdiv(ans, cc); // Γ(a) * Γ(b) / Γ(c)
dc := cbiground(dc, dpcs);
ans := cdiv(ans, dc); // Γ(a) * Γ(b) / Γ(c) / Γ(d)
result := 0;
end;
if (abs(af) + abs(bf)) > (abs(cf) + abs(df)) then begin
result := 1;
ans.r := bigdecimal.One;
ans.i := bigdecimal.Zero;
end;
if (abs(af) + abs(bf)) < (abs(cf) + abs(df)) then begin
result := 0;
ans.r := bigdecimal.Zero;
ans.i := bigdecimal.Zero;
end;
end;
// z > 1 Γ値のみ補正計算
// c < 0 b < 0 c < 0 は x < 1 のルーチンで計算されます
procedure Hypergeometric_function_of_NO_delt(a, b, c, z : cbig; eps : bigdecimal; var ans : cbig; var n, f : integer);
const
LNEPS = '1e-100';
var
g1, g2 , mzhma, mzhmb, mz : cbig;
onepamc, onepbmc, onepamb, onemapb : cbig;
ma, mb, sa, sb, tmc : cbig;
onesz, fa, fb, cone : cbig;
amb, bma, cma, cmb : cbig;
inf1, inf2, f1, f2 : integer;
dpcs : integer;
abig, bbig, ccbig, zbig, ansbig, czero : cbig;
epsbig, epsln, btwo : Bigdecimal;
n1, n2 : integer;
begin
dpcs := BigDecimal.DefaultPrecision;
epsln := LNEPS;
abig := a;
bbig := b;
ccbig := c;
zbig := z;
epsbig := eps;
cone.r := bigdecimal.One;
cone.i := bigdecimal.Zero;
czero.r := bigdecimal.Zero;
czero.i := bigdecimal.Zero;
btwo := bigdecimal.Two;
amb := csub(abig, bbig); // a-b
bma := csub(bbig, abig); // b-a
cma := csub(ccbig, abig); // c-a
cmb := csub(ccbig, bbig); // c-b
mz := cchs(zbig); // -z
ma := cchs(abig); // -a
mb := cchs(bbig); // -b
mzhma := pow_big(mz, ma, epsln); // (-z)^-a
mzhmb := pow_big(mz, mb, epsln); // (-z)^-b
tmc.r := abig.r + bigdecimal.One; // a + 1
tmc.i := abig.i;
onepamc := csub(tmc, ccbig); // 1+a-c
onepamb := csub(tmc, bbig); // 1+a-b
tmc.r := bbig.r + bigdecimal.One; // b + 1
tmc.i := bbig.i;
onepbmc := csub(tmc, ccbig); // 1+b-c
onemapb := csub(tmc, abig); // 1-a+b
onesz := cdiv(cone, zbig); // 1/z
// 1+a-b <=0 の時 無限大の判定 2F1(a, b, c, z)の c<=0 による判定
if zeroorounderbig(onepamb) then begin
// 1+a-c <=0 の時
if zeroorounderbig(onepamc) then begin
// 1+a-c <= 1+a-b
if onepamc.r <= onepamb.r then begin
f := 128; // 無限大フラグセット
exit;
end;
end
// 1+a-c > 0 の時
else begin
f := 128; // 無限大フラグセット
exit;
end;
end;
// 1-a+b <= 0 の時 無限大の判定 2F1(a, b, c, z)の c<=0 による判定
if zeroorounderbig(onemapb) then begin
// 1+b-c <=0 の時
if zeroorounderbig(onepbmc) then begin
// 1+b-c <= 1-a+b
if onepbmc.r <= onemapb.r then begin
f := 128; // 無限大フラグセット
exit;
end;
end
// 1+b-c > 0 の時
else begin
f := 128; // 無限大フラグセット
exit;
end;
end;
f1 := 0;
Hypergeometric_functionbig(abig, onepamc, onepamb, onesz, epsbig, sa, n1, f1); // 2F1(a, 1+a-c. 1+a-b, 1/z)
f2 := 0;
Hypergeometric_functionbig(bbig, onepbmc, onemapb, onesz, epsbig, sb, n2, f2); // 2F1(b, 1+b-c, 1-a+b, 1/z)
inf1 := gammaCalcbig(ccbig, bma, bbig, cma, g1);
tmc := cmul(g1, mzhma); // Γ(c) * Γ(b-a) / Γ(b) / Γ(c-a) * (-z)^-a
fa := cmul(tmc, sa); // Γ(c) * Γ(b-a) / Γ(b) / Γ(c-a) * (-z)^-a * 2F1(a)
inf2 := gammaCalcbig(ccbig, amb, abig, cmb, g2);
tmc := cmul(g2, mzhmb); // Γ(c) * Γ(a-b) / Γ(a) / Γ(c-b) * (-z)^-b
fb := cmul(tmc, sb); // Γ(c) * Γ(a-b) / Γ(a) / Γ(c-b) * (-z)^-b * 2F1(b)
if (f1 = -1) or (f1 = 1) then f := 16;
if (f2 = -1) or (f2 = 1) then f := 16;
if inf1 =1 then f := 16;
if inf2 =1 then f := 16;
if (f1 = -2) or (f2 = -2) then f := -2;
// tmc := cbiground(fa, 40);;
// form1.memo1.Lines.Append(' fa ' + tmc.r.ToString);
// tmc := cbiground(fb, 40);;
// form1.memo1.Lines.Append(' fb ' + tmc.r.ToString);
ansbig := cadd(fa, fb);
ansbig := cbiground(ansbig, dpcs);
btwo := btwo.RoundToPrecision(dpcs);
if aeqb(amb, czero) then // a = b 時は fa=fbとなり 解はfa 又は fbとなります
ans := cdivb(ansbig, btwo)
else
ans := ansbig;
if n1 >= n2 then n := n1
else n := n2;
end;
// z > 1 近似計算
// c < 0 b < 0 c < 0 は x < 1 のルーチンで計算されます
procedure Hypergeometric_function_of_first_kind(a, b, c, amb, bma, cma, cmb, aeb, z : cbig; eps
: bigdecimal; var ans : cbig; var n, f : integer);
const
LNEPS = '1e-100';
var
ga, gb, gc, gamb, gbma : cbig;
gcma, gcmb, mzhma, mzhmb, mz : cbig;
onepamc, onepbmc, onepamb, onemapb: cbig;
ma, mb, sa, sb, tmc : cbig;
onesz, fa, fb : cbig;
f1, f2 : integer;
abig, bbig, ccbig, zbig, ansbig, czero : cbig;
ambbig, bmabig, cmabig, cmbbig, aebbig : cbig;
epsbig, epsln, btwo : Bigdecimal;
dpcs : integer;
n1, n2 : integer;
// ctmp : cbig;
begin
dpcs := BigDecimal.DefaultPrecision;
epsln := LNEPS;
abig := a;
bbig := b;
ccbig := c;
zbig := z;
epsbig := eps;
ambbig := amb;
bmabig := bma;
cmabig := cma;
cmbbig := cmb;
aebbig := aeb;
czero.r := bigdecimal.Zero;
czero.i := bigdecimal.Zero;
btwo := bigdecimal.Two;
gammabig(abig, ga); // Γ(a)
gammabig(bbig, gb); // Γ(b)
gammabig(ccbig, gc); // Γ(c)
gammabig(ambbig, gamb); // Γ(a-b)
gammabig(bmabig, gbma); // Γ(b-a)
gammabig(cmabig, gcma); // Γ(c-a)
gammabig(cmbbig, gcmb); // Γ(c-b)
mz := cchs(zbig); // -z
ma := cchs(abig); // -a
mb := cchs(bbig); // -b
mzhma := pow_big(mz, ma, epsln); // (-z)^-a
mzhmb := pow_big(mz, mb, epsln); // (-z)^-a
tmc.r := bigdecimal.One; // 1
tmc.i := bigdecimal.Zero;
onepamc := csub(tmc, cmabig); // 1+a-c
onepbmc := csub(tmc, cmbbig); // 1+b-c
onepamb := cadd(tmc, ambbig); // 1+a-b
onemapb := cadd(tmc, bmabig); // 1-a+b
onesz := cdiv(tmc, zbig); // 1/z
Hypergeometric_functionbig(abig, onepamc, onepamb, onesz, epsbig, sa, n1, f1); // 2F1(a, 1+a-c. 1+a-b, 1/z)
// ctmp := cbiground(sa, 40);
// form1.memo1.Lines.Append('loop = ' + intTostr(n) + ' sa ' + ctmp.r.ToString);
// form1.memo1.Lines.Append(' ' + 'sai ' + ctmp.i.ToString + ' i');
// BR := false; // 割込みフラグ解除
Hypergeometric_functionbig(bbig, onepbmc, onemapb, onesz, epsbig, sb, n2, f2); // 2F1(b, 1+b-c, 1-a+b, 1/z)
// ctmp := cbiground(sb, 40);
// form1.memo1.Lines.Append('loop = ' + intTostr(n) + ' sb ' + ctmp.r.ToString);
// form1.memo1.Lines.Append(' ' + 'sbi ' + ctmp.i.ToString + ' i');
tmc := cmul(gc, gbma); // Γ(c) * Γ(b-a)
tmc := cbiground(tmc, dpcs);
gb := cbiground(gb, dpcs);
tmc := cdiv(tmc, gb); // Γ(c) * Γ(b-a) / Γ(b)
tmc := cbiground(tmc, dpcs);
gcma := cbiground(gcma, dpcs);
tmc := cdiv(tmc, gcma); // Γ(c) * Γ(b-a) / Γ(b) / Γ(c-a)
tmc := cmul(tmc, mzhma); // Γ(c) * Γ(b-a) / Γ(b) / Γ(c-a) * (-z)^-a
fa := cmul(tmc, sa); // Γ(c) * Γ(b-a) / Γ(b) / Γ(c-a) * (-z)^-a * 2F1(a)
tmc := cmul(gc, gamb); // Γ(c) * Γ(a-b)
tmc := cbiground(tmc, dpcs);
ga := cbiground(ga, dpcs);
tmc := cdiv(tmc, ga); // Γ(c) * Γ(a-b) / Γ(a)
gcmb := cbiground(gcmb, dpcs);
tmc := cdiv(tmc, gcmb); // Γ(c) * Γ(a-b) / Γ(a) / Γ(c-b)
tmc := cmul(tmc, mzhmb); // Γ(c) * Γ(a-b) / Γ(a) / Γ(c-b) * (-z)^-b
fb := cmul(tmc, sb); // Γ(c) * Γ(a-b) / Γ(a) / Γ(c-b) * (-z)^-b * 2F1(b)
ansbig := cadd(fa, fb); // Σ
// a = b 時は fa=fbとなり 解はfa 又は fbとなりますので1/2にします。
ansbig := cbiground(ansbig, dpcs);
btwo := btwo.RoundToPrecision(dpcs);
if aeqb(aebbig, czero) then ansbig := cdivb(ansbig, btwo);
if (f1 = 1) or (f1 = 2) then f := 16;
if (f2 = 1) or (f2 = 2) then f := 16;
if n1 >= n2 then n := n1
else n := n2;
ans := ansbig;
end;
// z=1 超幾何定理計算
procedure Hypergeometric_function_zeq1(a, b, c, z : cbig; eps : bigdecimal; var ans : cbig; var n, f : integer);
var
cmamb, cma, cmb, tmp: cbig;
gc, gcma, gcmb, gcmamb : cbig;
abig, bbig, ccbig, zbig, ansbig, czero : cbig;
dpcs : integer;
begin
dpcs := BigDecimal.DefaultPrecision;
abig := a;
bbig := b;
ccbig := c;
zbig := z;
czero.r := bigdecimal.Zero;
czero.i := bigdecimal.Zero;
f := 0;
n := 0;
cmamb := csub(ccbig, abig); // c - a
cmamb := csub(cmamb, bbig); // c - a - b
if cmamb.r <= czero.r then begin // Re(c-a-b) <= 0
f := 8; // ∞±符号計算フラグ
ansbig := czero;
exit;
end;
// Re(c-a-b) > 0 時の計算
cma := csub(ccbig, abig);
cmb := csub(ccbig, bbig);
gammabig(ccbig, gc); // Γ(c)
gammabig(cma, gcma); // Γ(c-a)
gammabig(cmb, gcmb); // Γ(c-b)
gammabig(cmamb, gcmamb); // Γ(c-a-b)
tmp := cmul(gc, gcmamb); // Γ(c) * Γ(c-a-b)
tmp := cbiground(tmp, dpcs);
gcma := cbiground(gcma, dpcs);
tmp := cdiv(tmp, gcma); // Γ(c) * Γ(c-a-b) / Γ(c-a)
gcmb := cbiground(gcmb, dpcs);
ansbig := cdiv(tmp, gcmb); // Γ(c) * Γ(c-a-b) / Γ(c-a) / Γ(c-b)
ans := ansbig;
end;
// z < -1 -1>z>-∞ 実数部の値が-1より小さい場合の専用計算
procedure Hypergeometric_function_mz(a, b, c, z : cbig; eps : bigdecimal; var ans : cbig; var n, f : integer);
const
LNEPS = '1e-100';
var
onemz, bma, cma, cmb, ambp1 : cbig;
amb, bmap1 : cbig;
gc, gbma, gb, gcma : cbig;
gamb, ga, gcmb : cbig;
onec, tmp, tmc, invz : cbig;
g1, g2, onemzhma, onemzhmb : cbig;
abig, bbig, ccbig, zbig, ansbig, czero : cbig;
// tmf : bigdecimal;
f1, f2, dpcs : integer;
epsln, twobig, epsbig : bigdecimal;
n1, n2 : integer;
begin
dpcs := BigDecimal.DefaultPrecision;
abig := a;
bbig := b;
ccbig := c;
zbig := z;
epsbig := eps;
czero.r := bigdecimal.Zero;
czero.i := bigdecimal.Zero;
onec.r := bigdecimal.One;
onec.i := bigdecimal.Zero;
epsln := LNEPS;
twobig := bigdecimal.Two;
onemz := csub(onec, zbig);
zbig := cbiground(zbig, dpcs);
onec := cbiground(onec, dpcs);
invz := cdiv(onec, onemz); // 1/z
bma := csub(bbig, abig); // b-a
cma := csub(ccbig, abig); // c-a
amb := csub(abig, bbig); // a-b
cmb := csub(ccbig, bbig); // c-b
ambp1 := cadd(amb, onec); // a-b+1
bmap1 := cadd(bma, onec); // b-a+1
gammabig(abig, ga); // Γ(a)
gammabig(bbig, gb); // Γ(b)
gammabig(ccbig, gc); // Γ(c)
gammabig(bma, gbma); // Γ(b-a)
gammabig(cma, gcma); // Γ(c-a)
gammabig(amb, gamb); // Γ(a-b)
gammabig(cmb, gcmb); // Γ(c-b)
tmp := cchs(abig); // -a
onemzhma := pow_big(onemz, tmp, epsln); // (1-z)^-a
tmp := cchs(bbig); // -b
onemzhmb := pow_big(onemz, tmp, epsln); // (1-z)^-b
gc := cbiground(gc, dpcs);
gb := cbiground(gb, dpcs);
tmp := cdiv(gc, gb); // Γ(c)/Γ(b)
tmp := cmul(tmp, gbma); // Γ(c)/Γ(b) * Γ(bma)
tmp := cbiground(tmp, dpcs);
gcma := cbiground(gcma, dpcs);
g1 := cdiv(tmp, gcma); // Γ(c)/Γ(b) * Γ(bma)/Γ(c-a)
ga := cbiground(ga, dpcs);
tmp := cdiv(gc, ga); // Γ(c)/Γ(a)
tmp := cmul(tmp, gamb); // Γ(c)/Γ(b) * Γ(amb)
tmp := cbiground(tmp, dpcs);
gcmb := cbiground(gcmb, dpcs);
g2 := cdiv(tmp, gcmb); // Γ(c)/Γ(b) * Γ(amb)/Γ(c-b)
f1 := 0;
Hypergeometric_functionbig(abig, cmb, ambp1, invz, epsbig, tmc, n1, f1);
tmc := cmul(tmc, onemzhma); // F*(1-z)^^a
tmc := cmul(tmc, g1); // F*(1-z)^a * Γ/Γ
f2 := 0;
Hypergeometric_functionbig(bbig, cma, bmap1, invz, epsbig, ansbig, n2, f2);
ansbig := cmul(ansbig, onemzhmb); // F*(1-z)^b
ansbig := cmul(ansbig, g2); // F*(1-z)^b * Γ/Γ
ansbig := cadd(tmc, ansbig);
if aeqb(amb, czero) then begin // a=bの時は、1/2
ansbig := cbiground(ansbig, dpcs);
twobig := twobig.RoundToPrecision(dpcs);
ansbig := cdivb(ansbig, twobig);
end;
if f1 <> 0 then f := f1;
if f2 <> 0 then f := f2;
if n1 >= n2 then n := n1
else n := n2;
ans := cbiground(ansbig, dpcs);
end;
// 0.5 < z < 1
procedure Hypergeometric_function_harftone(a, b, c, z : cbig; eps : bigdecimal; var ans : cbig; var n, f : integer);
const
LNEPS = '1e-100';
var
abig, bbig, ccbig, zbig, ansbig : cbig;
cmamb, cma, cmb, apbmcp1 : cbig;
apbmc, cmambp1, tmc, onemz, onemzhcab : cbig;
ga, gb, gc, g1, g2: cbig;
gcmamb, gapbmc, tmp, onec : cbig;
gcma, gcmb : cbig;
czero : cbig;
epsln, epsbig : bigdecimal;
f1, f2, dpcs: integer;
n1, n2, : integer;
begin
dpcs := BigDecimal.DefaultPrecision;
czero.r := bigdecimal.Zero;
czero.i := bigdecimal.Zero;
onec.r := bigdecimal.One;
onec.i := bigdecimal.Zero;
epsln := LNEPS;
abig := a;
bbig := b;
ccbig := c;
zbig := z;
epsbig := eps;
cma := csub(ccbig, abig); // c-a
cmb := csub(ccbig, bbig); // c-b
cmamb := csub(cma, bbig); // c-a-b
tmp := cadd(abig, bbig); // a+b
apbmc := csub(tmp, ccbig); // a+b-c
apbmcp1 := cadd(apbmc, onec); // a+b-c+1
cmambp1 := cadd(cmamb, onec); // c-a-b+1
onemz := csub(onec, zbig); // 1-z
gammabig(abig, ga); // Γ(a)
gammabig(bbig, gb); // Γ(b)
gammabig(ccbig, gc); // Γ(c)
gammabig(cma, gcma); // Γ(c-a)
gammabig(cmb, gcmb); // Γ(c-b)
gammabig(cmamb, gcmamb); // Γ(c-a-b)
gammabig(apbmc, gapbmc); // Γ(a+b-c)
gc := cbiground(gc, dpcs);
gcma := cbiground(gcma, dpcs);
tmp := cdiv(gc, gcma); // Γ(c)/Γ(c-a)
tmp := cmul(tmp, gcmamb); // Γ(c)/Γ(c-a)*Γ(c-a-b)
tmp := cbiground(tmp, dpcs);
gcmb := cbiground(gcmb, dpcs);
g1 := cdiv(tmp, gcmb); // g1 = Γ(c)/Γ(c-a)*Γ(c-a-b)/Γ(c-b)
gc := cbiground(gc, dpcs);
ga := cbiground(ga, dpcs);
tmp := cdiv(gc, ga); // Γ(c)/Γ(a)
tmp := cmul(tmp, gapbmc); // Γ(c)/Γ(a)*Γ(a+b-c)
gb := cbiground(gb, dpcs);
g2 := cdiv(tmp, gb); // g2 = Γ(c)/Γ(a)*Γ(a+b-c)/Γ(b)
onemzhcab := pow_big(onemz, cmamb, epsln); // (1-z)^(c-a-b)
f1 := 0;
Hypergeometric_functionbig(abig, bbig, apbmcp1, onemz, epsbig, tmc, n1, f1);
tmc := cmul(tmc, g1);
f2 := 0;
Hypergeometric_functionbig(cma, cmb, cmambp1, onemz, epsbig, ansbig, n2, f2);
ansbig := cmul(ansbig, g2);
ansbig := cmul(ansbig, onemzhcab);
ansbig := cadd(ansbig, tmc);
if f1 <> 0 then f := f1;
if f2 <> 0 then f := f2;
if n1 >= n2 then n := n1
else n := n2;
ans := cbiground(ansbig, dpcs);
end;
//------------------------------------------------------------------------------
var
astd, bstd, cstd, zstd : bigdecimal; // arcsin arctan用 実数部
// arcsin計算
procedure TForm1.arsinBtnClick(Sender: TObject);
var
ch : integer;
ars : double;
tmp0, tmp1, tmp2 : bigdecimal;
begin
val(arsinEdit.Text, ars, ch);
if ch <> 0 then begin
application.MessageBox('arsin の値に間違いがあります。','注意',0);
exit;
end;
if abs(ars) > 1 then begin
application.MessageBox('arsin の値は±1迄にして下さい。','注意',0);
exit;
end;
tmp0 := arsinEdit.Text;
if (abs(ars) < 0.75) or (abs(ars) = 1) then TN := 2
else TN := 1;
astd := '0.5';
if (abs(ars) < 0.75) or (abs(ars) = 1) then bstd := '0.5'
else bstd := '1';
cstd := '1.5';
if (abs(ars) < 0.75) or (abs(ars) = 1) then zstd := arsinEdit.Text
else begin
tmp1 := tmp0 * tmp0; // ars * ars
tmp2 := one - tmp1; // 1 - ars * ars
tmp1 := tmp2.Sqrt(tmp2, 100); // sqrt(1 - ars * ars)
tmp0 := tmp0.RoundToPrecision(100);
tmp2 := tmp0 / tmp1; // ars / sqrt(1 - ars * ars)
tmp2 := tmp2.RoundToPrecision(50);
zstd := tmp2.ToString;
end;
DS := 2;
Button1Click(nil);
end;
// arctan計算
procedure TForm1.artanBtnClick(Sender: TObject);
var
ch : integer;
art : double;
tmp0, tmp1, tmp2 : bigdecimal;
begin
val(ArtanedEdit.Text, art, ch);
if ch <> 0 then begin
application.MessageBox('artan の値に間違いがあります。','注意',0);
exit;
end;
tmp0 := ArtanedEdit.Text;
if (abs(art) < 0.75) or (abs(art) > 1.4) then TN := 1
else TN := 2;
astd := '0.5';
if (abs(art) < 0.75) or (abs(art) > 1.4) then bstd := '1'
else bstd := '0.5';
cstd := '1.5';
if (abs(art) < 0.75) or (abs(art) > 1.4) then zstd := artanededit.Text
else begin
tmp1 := tmp0 * tmp0; // art * art
tmp2 := tmp1 + one; // 1 + art * art
tmp1 := tmp2.Sqrt(tmp2, 100); // sqrt(1 + art * art)
tmp1 := tmp2.Sqrt(tmp2, 100); // sqrt(1 - ars * ars)
tmp0 := tmp0.RoundToPrecision(100);
tmp2 := tmp0 / tmp1; // art / sqrt(1 + art * art)
zstd := tmp2;
end;
DS := 1;
Button1Click(nil);
end;
//------------------------------------------------------------------------------
// 計算打切り
procedure TForm1.BitBtn1Click(Sender: TObject);
begin
BR := True;
button1.Enabled := True;
end;
// 数値の後ろのゼロ消去
function ZeroErase(s : string): string;
const
EP = 'e';
ZC = '0';
dt = '.';
var
c : char;
i, j, k, l : integer;
begin
l := length(s);
j := 1;
for i := 1 to l do begin
c := s[i];
if c = EP then begin
j := i - 1;
break;
end;
j := i;
end;
result := '';
if j < l then begin
for i := l downto j + 1 do
result := s[i] + result;
end;
K := 1;
for i := j downto 1 do begin
c := s[i];
if c <> ZC then begin
k := i;
if c = DT then k := k + 1;
break;
end;
end;
for i := k downto 1 do
result := s[i] + result;
end;
// 入力値の最大値最小値のチェック
function inbigcheck(s, xtext: string): boolean;
const
MAXSTR = '200';
MINSTR = '1e-100';
var
max, min, x: bigdecimal;
begin
result := false;
try
x := xtext;
except
on EConverterror do begin
MessageDlg(s + ' の値に間違いがあります。', mtError, [mbOK], 0);
exit;
end;
end;
max := MAXSTR;
min := MinSTR;
if x.Abs(x) > max then begin
application.MessageBox(pchar('abs(' + s + ')の値が大きすぎます。' + #13#10 +
'±' + MAXSTR + 'が限度です。'),'注意',0);
exit;
end;
if (x.Abs(x) < min) and (x.Abs(x) <> zero) then begin
application.MessageBox(pchar('abs(' + s + ')の値が小さすぎます。' + #13#10 +
'±' + MINSTR + 'が限度です。'),'注意',0);
exit;
end;
result := true;
end;
// 入力チェック
function TForm1.inputcheck(var pre: integer): boolean;
var
chd: double;
ch : integer;
begin
result := false;
if not inbigcheck('a 実数', aedit.Text) then exit;;
if not inbigcheck('b 実数', bedit.Text) then exit;;
if not inbigcheck('c 実数',cedit.Text) then exit;;
if not inbigcheck('z 実数', zedit.Text) then exit;;
if not inbigcheck('aの虚数', iaedit.Text) then exit;;
if not inbigcheck('bの虚数', ibedit.Text) then exit;;
if not inbigcheck('cの虚数', icedit.Text) then exit;;
if not inbigcheck('zの虚数', izedit.Text) then exit;;
val(precisionedit.Text, pre, ch);
if ch <> 0 then begin
application.MessageBox('有効桁数 の値に間違いがあります。','注意',0);
exit;
end;
if pre < 100 then begin
application.MessageBox('有効桁数 は100以上にして下さい。','注意',0);
exit;
end;
if pre > 2000 then begin
application.MessageBox('有効桁数 は2000以下にして下さい。','注意',0);
exit;
end;
val(epsedit.Text, chd, ch);
if ch <> 0 then begin
application.MessageBox('収束判定値に間違いがあります。','注意',0);
exit;
end;
if chd < 1e-200 then begin
application.MessageBox('収束判定値は1e-200より大きくして下さい。','注意',0);
exit;
end;
if chd > 1e-1 then begin
application.MessageBox('収束判定値は1e-1より小さく下さい。','注意',0);
exit;
end;
if form1.deltbox.Checked = true then begin
val(deltedit.Text, chd, ch);
if ch <> 0 then begin
application.MessageBox('Δ値に間違いがあります。','注意',0);
exit;
end;
chd := abs(chd);
if chd > 1e-10 then begin
application.MessageBox('Δ値は1e-10より小さく下さい。','注意',0);
exit;
end;
if chd < 1e-100 then begin
application.MessageBox('Δ値は1e-100より大きく下さい。','注意',0);
exit;
end;
end;
val(maxloopedit.Text, chi, ch);
if ch <> 0 then begin
application.MessageBox('最大Loop数に間違いがあります。','注意',0);
exit;
end;
if chi < 1 then begin
application.MessageBox('最大Loop数は1万以上にしてください。','注意',0);
exit;
end;
if chi > 100 then begin
application.MessageBox('最大Loop数は100万以下にしてください。','注意',0);
exit;
end;
result := true;
end;
// 計算開始
procedure TForm1.Button1Click(Sender: TObject);
label
EXT, TN0E, ZG01, ZG02, ZG03;
const
LNEPS = '1e-100';
var
a, b, c, z, ans : cbig;
mz2, tans, tmc, onec, zeroc : cbig;
n, pre : integer;
f : integer;
eps, az: bigdecimal;
amb, bma, cma, cmb, aeb : cbig;
d1, d2 : bigdecimal;
XLE : boolean;
ap, bp, cp : cbig;
am, bm, cm : cbig;
zback, aback, zbackp : cbig;
dnine, tmf, absz, epsln : bigdecimal;
df, dpcs : integer;
delt : bigdecimal;
EpslimitF : boolean;
nabsz : bigdecimal;
PAFF : boolean;
n1, n2 : integer;
// 1E-35 以下はゼロにセット
procedure zerounde1em35(var ans: cbig);
begin
d1 := '1E-35';
tmf := ans.r.Abs(ans.r);
if tmf < d1 then ans.r := bigdecimal.Zero;
tmf := ans.i.Abs(ans.i);
if tmf < d1 then ans.i := bigdecimal.Zero;
end;
// 1E-42 以下はゼロにセット
procedure zerounde1em42(var ans: cbig);
begin
d1 := '1E-42';
tmf := ans.r.Abs(ans.r);
if tmf < d1 then ans.r := bigdecimal.Zero;
tmf := ans.i.Abs(ans.i);
if tmf < d1 then ans.i := bigdecimal.Zero;
end;
// 1E-52 以下はゼロにセット
procedure zerounde1em52(var ans: cbig);
begin
d1 := '1E-52';
tmf := ans.r.Abs(ans.r);
if tmf < d1 then ans.r := bigdecimal.Zero;
tmf := ans.i.Abs(ans.i);
if tmf < d1 then ans.i := bigdecimal.Zero;
end;
// 表示桁数を収束判定地に合わせる
procedure epslimit(var ans: cbig; epstext: string);
const
mch = '-';
mcd = '.';
var
str, nstr : string;
lng, pc, flng : integer;
begin
str := epstext;
lng := length(str);
pc := pos(mch, str);
if pc = 0 then begin
ans := cbiground(ans, 1);
exit;
end;
nstr := copy(str, pc+1, lng - pc); // 1e-(xx) nstr = xx
flng := strToint(nstr);
ans := cbiground(ans, 100);
str := ZeroErase(ans.r.ToString);
pc := pos(mcd, str); // xx.zzzzzzzzzz の'.'の位置
lng := pc + flng - 1; // 表示桁数
ans := cbiground(ans, lng);
nstr := ZeroErase(ans.r.ToString); // ans.re表示桁数文字変換
str := ZeroErase(ans.i.ToString); // ans.im表示桁数文字変換
ans.r := nstr;
ans.i := str;
end;
begin
if not ((DS = 1) or (DS = 2)) then begin // 通常の超幾何関数
// 入力チェック
if not inputcheck(pre) then exit;
// 入力値 多倍長
a.r := aedit.Text;
b.r := bedit.Text;
c.r := cedit.Text;
z.r := zedit.Text;
a.i := iaedit.Text;
b.i := ibedit.Text;
c.i := icedit.Text;
z.i := izedit.Text;
delt := deltedit.Text;
DS := 0;
end
else begin // arcsin or arctan
a.r := astd;
b.r := bstd;
c.r := cstd;
z.r := zstd;
a.i := zero;
b.i := zero;
c.i := zero;
z.i := zero;
end;
button1.Enabled := False;
epsln := LNEPS; // 収束判定値
dpcs := strtoint(precisionedit.Text);
if dpcs <> BigDecimal.DefaultPrecision then begin
BigDecimal.DefaultPrecision := dpcs;
Bernoulli_number_BigInteger;
end;
// dpcs := BigDecimal.DefaultPrecision; // 有効桁数
maxloops := strtoint(MaxLoopEdit.Text) * 10000; // 最大ループ数
disploops := maxloops div 200; // 収束状態表示間隔
BR := false; // 停止フラグリセット
BRB := false;
EpslimitF := false; // 表示桁数設定フラグ
memo1.Clear;
memo1.Lines.Append('計算中');
application.ProcessMessages;
eps := epsedit.Text; // 2F1収束判定地
epsback := '200';
// 値設定
zeroc.r := bigdecimal.Zero; // c0
zeroc.i := bigdecimal.Zero;
onec.r := bigdecimal.One; // c1
onec.i := bigdecimal.Zero;
absz := cabs(z, dpcs); // |z|
f := 0;
n := 0;
// a>b なら入れ替え
ap.r := cabs(a, dpcs);
bp.r := cabs(b, dpcs);
if ap.r > bp.r then begin
tmc := a;
a := b;
b := tmc;
end;
ans.r := bigdecimal.Zero;
ans.i := bigdecimal.Zero;
az := z.r.Abs(z.r); // |z.re|
zback := z; // z -> zback
XLE := false; // 近似計算フラグリセット
if TN = 0 then begin // 通常計算
// z = 0
if aeqb(z, zeroc) then begin
memo1.Lines.Append('zの値がゼロです');
memo1.Lines.Append(' 1.0');
memo1.Lines.Append(' +0.0i');
goto EXT;
end;
// 複素数zの角度計算
tmf := arg_big(z);
tmf := tmf.RoundToPrecision(20);
tmf := tmf.Abs(tmf);
if tmf = zero then memo1.Lines.Append('|arg(z)| = ' + '0.0')
else memo1.Lines.Append('|arg(z)| = ' + tmf.ToString);
tmc := z;
tmc := cchs(tmc);
tmc.r := tmc.r + one; // 1-z
tmf := arg_big(tmc);
tmf := tmf.RoundToPrecision(20);
tmf := tmf.Abs(tmf);
if tmf = zero then memo1.Lines.Append('|arg(1-z)|= ' + '0.0')
else memo1.Lines.Append('|arg(1-z)|= ' + tmf.ToString);
// -------------------------------------------------------------------------
// 整数 (c <= 0 or a <= 0 or b <= 0) a,b,cの何れか又は全部が0を含み負の整数の場合
// zの値に関係なく通常の超幾何関数計算 Z<1の計算使用します。 二番目に確認
// /Z/の値が1より大きい場合aかb又はcがゼロになった時点で計算計算打ち切り
// cが先か同時にゼロになった場合は±∞となります。
// |z|の値が1より小さい場合は、a,bが先にゼロになるか、cがゼロになった時
// a,bがゼロになってないかで計算がかわります。
if zeroorounderbig(c) or (zeroorounderbig(a) or zeroorounderbig(b)) then begin
memo1.Lines.Append(' (整数a<=0) or (整数b<=0) or (整数c<=0) ');
Hypergeometric_functionbig_zero(a, b, c, z, eps, ans, n, f);
goto TN0E;
end;
//--------------------------------------------------------------------------
// z = 1 超幾何定理計算
if aeqb(z, onec) then begin
Hypergeometric_function_zeq1(a, b, c, z, eps, ans, n, f);
Memo1.Lines.Append(' z = 1 専用');
if f = 0 then begin
Memo1.Lines.Append(' Re(c - a - b) > 0');
goto TN0E;
end;
// ∞符号設定 z=1 計算し∞±符号設定
if f = 8 then begin
Hypergeometric_functionbig(a, b, c, z, eps, ans, n, f);
goto TN0E;
end;
end;
//--------------------------------------------------------------------------
// (c-a) <=0 整数 or (c-b)<=0 整数
// (1-z)^(c-a-b)2F1(c-a,c-b;c;z)
// Euler transformation
if checkbox8.Checked = false then begin
am := csub(c, a);
bm := csub(c, b);
if zeroorounderbig(am) or zeroorounderbig(bm) then begin
Hypergeometric_functionbig_zero(am, bm, c, z, eps, cm, n, f);
tmc := csub(csub(c,a), b);
tmc := pow_big(csub(onec, z), tmc, epsln);
ans := cmul(cm, tmc);
memo1.Lines.Append('Euler transformation (1-z)^(c-a-b)2F1(c-a,c-b;c;z)');
goto TN0E;
end;
end;
// |Z| > 1 実数部0の時
if (absz > one) and (z.r = bigdecimal.Zero) then begin
goto ZG02;
end;
//--------------------------------------------------------------------------
// z.re < 0 0.8< |z| < 2 -∞でも可 -2迄に限定 デバッグの為 a, b, c に非整数がある場合
// 非整数だとpfaff変換が出来ないため 1/(1-z)で計算
ap.r := a.r.Frac;
bp.r := b.r.Frac;
cp.r := c.r.Frac;
df := 0;
if (ap.r<> zero) or (bp.r <> zero) or (cp.r <> zero) then df := 1;
if (a.i <> zero) or (b.i <> zero) or (c.i <> zero) then df := df or 2;
if (checkbox5.Checked = true) and (df <> 0) then begin
// z,re<0 and |z|>0.8 and |z|<2
d1 := '0.8';
if (z.r < zero) and (absz > d1) and (absz < two) then begin
amb := csub(a, b); // a-b
bma := csub(b, a); // b-q
cma := csub(c, a); // c-a
ap := cadd(amb, onec); // a-b + 1
bp := cadd(bma, onec); // b-a + 1
// a,b,c<=0 整数は前で処理されます
// c以外で無限大になるか確認
df := 0; // ∞になるか確認
if zeroorounderbig(amb) then df := df or 1; // a-b
if zeroorounderbig(bma) then df := df or 2; // b-a
if zeroorounderbig(ap) then df := df or 4; // a-b+1
if zeroorounderbig(bp) then df := df or 8; // b-a+1
// a=b=c 確認
if aeqb(amb, zeroc) and aeqb(cma, zeroc) then df := 16; // Γ(0)/Γ(0) になります。
if (df = 0) or (df = 16) then begin
Hypergeometric_function_mz(a, b, c, z, eps, ans, n, f );
memo1.Lines.Append('z < 0 0.8<|z|<2');
memo1.Lines.Append('変換 1/(1-z) Δ無し');
goto TN0E;
end
else begin
d1 := '1E-20';
if deltbox.Checked = true then d1 := delt;
cp := caddb(c, d1);
ap := caddb(a, d1);
Hypergeometric_function_mz(ap, b, cp, z, eps, tmc, n1, f);
cm := csubb(c, d1);
am := csubb(a, d1);
Hypergeometric_function_mz(am, b, cm, z, eps, ans, n2, f);
if n1 >= n2 then n := n1
else n := n2;
tmc := cadd(tmc, ans);
tmc := cbiground(tmc, dpcs);
two := two.RoundToPrecision(dpcs);
ans := cdivb(tmc, two);
memo1.Lines.Append('z < 0 0.8<|z|<2');
memo1.Lines.Append('変換 1/(1-z) a,c±Δ計算');
XLE := true;
goto TN0E;
end;
end;
end;
//--------------------------------------------------------------------------
// f(a, b, b, z) z<>1
am := csub(c, a);
bm := csub(c, b);
if (aeqb(am, zeroc) or aeqb(bm, zeroc)) and not aeqb(z, onec) and not aeqb(z, zeroc) then begin
if aeqb(am, zeroc) then begin // am = 0
tmc := a; // a<->b
a := b;
b := tmc;
end;
ap := cchs(a); // -a
tmc := csub(onec, z); // 1-z
ans := pow_big(tmc, ap, epsln); // (1-z)^-a
memo1.Lines.Append('F(a, b, b, z) z <> 1');
goto TN0E;
end;
//--------------------------------------------------------------------------
// f(1,2,3,z) z<>1
if checkbox10.Checked = true then
if (a.r = one) and (b.r = two) and (c.r = three)
and (a.i = zero) and (b.i = zero) and (c.i = 0) and not aeqb(z, onec) then begin
am := csub(onec, z); // 1-z
ap := cadd(z, log_big(am, epsln, dpcs)); // z + log(1-z)
bm := cmulb(ap, two); // (z + log(1-z)) * 2
bm := cchs(bm); // -
cp := cmul(z, z); // z^2
bm := cbiground(bm, dpcs);
cp := cbiground(cp, dpcs);
ans := cdiv(bm, cp); // -((z + log(1-z)) * 2)/x^2
memo1.Lines.Append('F(1, 2, 3, z) z <> 1');
goto TN0E;
end;
//--------------------------------------------------------------------------
// a,a+1,c or b+1,b,c z>1 時の近似計算
ap := caddb(a, one);
bp := caddb(b, one);
if ap.r > bp.r then begin // ap > bp なら ap <-> bp
tmc := ap;
ap := bp;
bp := tmc;
end;
cp.r := bp.r - ap.r; // re(a),re(b) 差分 差分は0~+
tmf := a.r.Frac; // re(a)の小数部
// im(z) = 0 なら
if (checkbox4.Checked = true) then begin
// re(a)-re(b) = 1 虚数部im(a)=0 |z{>1 実数部re(z)>=0
d1 := '0.7';
if (cp.r = one) and (a.i = zero) and (absz > one) and (z.r >= d1) then begin
if (tmf <> zero) then begin // 小数部がゼロでなかったら 整数でなかったら
if (absz <= four) then begin // 1<=|z|<4 だったら
DS := 32; // 専用近似計算フラグセット 1-1/z
goto ZG01; // pfaff 変換不可
end
else begin // |z|>=4
DS := 16; // 近似計算フラグセット
goto ZG03; // pfaff 変換不要
end;
end
else begin // a, b が整数だったら
if (absz >four) then begin // /z/>=4 なら
DS := 16; // 近似計算フラグセット
goto ZG03; // pfaff 変換不要 /z/>1の計算へ
end
else begin // 1<=|z|<=4
DS := 32; // 専用近似計算フラグセット z' = 1-1/z
goto ZG01; // pfaff 変換不要
end;
end;
end
else begin
// a-b=1 im(a)=0 |z|>=1 re(z)<0
if (cp.r = one) and (a.i = zero) and (absz >= one) and (z.r < zero) then begin
DS := 0; // 近似計算なし
goto ZG02; // pfaff 変換
end;
end;
end;
ZG01:
//--------------------------------------------------------------------------
// a,a+1,c or b+1,b,c 1<z<2 時の近似計算 z'= 1-1/z 変換
// a,b,c 全て整数時は±Δ 非整数時は Δ0の時あり
if DS = 32 then begin
ap := cadd(a, b); // a+b
cm := csub(ap, c); // a+b-c
cp := cadd(cm, onec); // a+b-c+1
cma := csub(c, a); // c-a
am := csub(cma, b); // c-a-b
bp := cadd(am, onec); // c-a-b+1
df := 0;
if zeroorounderbig(c) then df := df or 1; // c
if zeroorounderbig(am) then df := df or 2; // c-a-b
if zeroorounderbig(cp) then df := df or 4; // a+b-c+1
if zeroorounderbig(cm) then df := df or 8; // a+b-c
if zeroorounderbig(bp) then df := df or 16; // c-a-b+1
if (df = 0) then begin // Γ無限大が無かったら and a=b
Hypergeometric_function_of_first_kind_aeb(a, b, c, z, eps, ans, n, f);
memo1.Lines.Append('変換 1-1/z Δ無し');
DS := 0; // Δ無しなので近似計算ではありません。
goto TN0E;
end;
d1 := '1E-20';
if deltbox.Checked = true then d1 := delt;
// d1 := '431E-21';
cp := csubb(c, d1);
Hypergeometric_function_of_first_kind_aeb(a, b, cp, z, eps, tmc, n1, f);
cm := caddb(c, d1);
Hypergeometric_function_of_first_kind_aeb(a, b, cm, z, eps, ans, n2, f);
if n1 >= n2 then n := n1
else n := n2;
tmc := cadd(tmc, ans);
tmc := cbiground(tmc, dpcs);
ans := cdivb(tmc, two);
memo1.Lines.Append('a,a+1,c or b+1,b,c 1<z<2');
memo1.Lines.Append('変換 1-1/z c±Δ計算');
XLE := true;
goto TN0E;
end;
//--------------------------------------------------------------------------
// 0.5 < z <= 1
if (checkbox6.Checked = true) then begin
d2 := '0.5';
ap.r := a.r.Frac;
bp.r := b.r.Frac;
cp.r := c.r.Frac;
tmf := '0.5';
if (absz > tmf) and (absz < one) and (z.r > d2)
and ((ap.r <> zero) or (bp.r <> zero) or (cp.r <> zero)) then begin
DS := 0;
ap := cadd(a, b); // a+b
cm := csub(ap, c); // a+b-c
amb := cadd(cm, onec); // a+b-c+1
cma := csub(c, a); // c-a
am := csub(cma, b); // c-a-b
bp := cadd(am, onec); // c-a-b+1
df := 0;
if zeroorounderbig(am) then df := df or 1; // c-a-b
if zeroorounderbig(amb) then df := df or 2; // a+b-c+1
if zeroorounderbig(cm) then df := df or 4; // a+b-c
if zeroorounderbig(bp) then df := df or 8; // c-a-b+1
if zeroorounderbig(c) then df := df or 16; // c
if df = 0 then begin
Hypergeometric_function_harftone(a, b, c, z, eps, ans, n, f);
memo1.Lines.Append('変換 1-z Δ無し');
goto TN0E;
end;
d1 := '226476e-34';
if deltbox.Checked = true then d1 := delt;
cp := caddb(c, d1);
Hypergeometric_function_harftone(a, b, cp, z, eps, tmc, n1, f);
cm := csubb(c, d1);
Hypergeometric_function_harftone(a, b, cm, z, eps, ans, n2, f);
if n1 >= n2 then n := n1
else n := n2;
tmc := cadd(tmc, ans);
tmc := cbiground(tmc, dpcs);
ans := cdivb(tmc, two);
memo1.Lines.Append('変換 1-z c±Δ計算');
XLE := true;
goto TN0E;
end;
end;
//--------------------------------------------------------------------------
// F a,a+1,c, z) or ( F b+1, b, c, z) |z| > 1
am := csub(b, a);
bm := csub(a, b);
if aeqb(am, onec) or aeqb(bm, onec) then begin
if absz > one then begin
goto ZG02; // pfaff変換へ
end;
end;
//--------------------------------------------------------------------------
// F(1, 1, 2, z) z <> 1
if checkbox9.Checked = true then begin
tmc := csub(c, onec); // c - (1+0i)
if aeqb(a, onec) and aeqb(b, onec) and aeqb(tmc, onec) and not aeqb(z, onec) and not aeqb(z, zeroc) then begin
tmc := csub(onec, z); // 1-z
tmc := log_big(tmc, epsln, dpcs); // ln(1-z)
tmc := cbiground(tmc, dpcs);
z := cbiground(z, dpcs);
ans := cdiv(tmc, z); // ln(1-z)/z
ans := cchs(ans); // -ln(1-z)/z
memo1.Lines.Append('F(1, 1, 2, z) z <> 1');
goto TN0E;
end;
end;
//--------------------------------------------------------------------------
// a = b, c / a = 2 0.6<z<2 1-1/z 変換
// cが整数 c<=0 の場合は、先に処理されるので、aのみ近似計算
// a = b, c / a = 2 の時には ±Δ近似計算以外なし
// a±Δ b±Δ c±Δ どれを使用しても結果は同じです
// re(z) =0 /z/=1 は不可
bp := csub(b, a); // a,b 差分 差分は0~+
d1 := '0.6';
if not aeqb(a, zeroc) then begin
c := cbiground(c, dpcs);
a := cbiground(a, dpcs);
cp := cdiv(c, a); // c/a
end;
if (checkbox2.Checked = true) then
// 0.6<|z| c/a=2 a=b z<>1
if (absz > d1) and (cp.r = two) and (cp.i = zero) and aeqb(bp, zeroc) and not aeqb(z, onec) then begin
// zの範囲 0.6 < |z| < 2
if (absz < two) and (absz <> one) and (z.r > d1) then begin
d1 := '3E-19';
if deltbox.Checked = true then d1 := delt;
ap := caddb(a, d1);
Hypergeometric_function_of_first_kind_aeb(ap, b, c, z, eps, tmc, n1, f);
am := csubb(a, d1);
Hypergeometric_function_of_first_kind_aeb(am, b, c, z, eps, ans, n2, f);
if n1 >= n2 then n := n1
else n := n2;
ans := cadd(tmc, ans);
ans := cbiground(ans, dpcs);
two := two.RoundToPrecision(dpcs);
ans := cdivb(ans, two);
memo1.Lines.Append('a = b, c / a = 2 0.6 < z < 2');
memo1.Lines.Append('変換 1-1/z a±Δ計算');
DS := 32; // 近似計算フラグ低精度
XLE := true; // 近似計算フラグ
goto TN0E;
end;
end;
//--------------------------------------------------------------------------
// a = b, c <> a, 1<z<= 2 a,b 非整数
// Γ計算に±∞無し 近似計算の必要なし確認 非整数時はΔ無多い
if not aeqb(a, zeroc) then begin
c := cbiground(c, dpcs);
a := cbiground(a, dpcs);
cp := cdiv(c, a); // c/a
end;
ap.r := a.r.Frac;
if (checkbox2.Checked = true) and (ap.r <> zero) and (bp.r = zero) and (bp.i = zero) and (absz > one)
and (cp.r <> two) and (absz <= two) then begin
ap := cadd(a, b); // a+b
ap := csub(ap, c); // a+b-c
am := csub(c, a); // c-a
am := csub(am, b); // c-a-b
// a+b-c c-a-b c
if not zeroorounderbig(ap) and not zeroorounderbig(am) and not zeroorounderbig(c) then begin
d1 := '0.6';
ap := cadd(ap, onec); // a+b-c+1
am := cadd(am, onec); // c-a-b+1
amb := csub(a, b);
// a+b-c+1 c-a-b+1 a=b RE(z) > 0.6
if not zeroorounderbig(ap) and not zeroorounderbig(am) and aeqb(amb, zeroc) and (z.r > d1) then begin
Hypergeometric_function_of_first_kind_aeb(a, b, c, z, eps, ans, n, f);
memo1.Lines.Append('a = b, 1<z<=2 ');
memo1.Lines.Append('変換 1-1/z Δ無し計算');
goto TN0E;
end;
end;
end;
//--------------------------------------------------------------------------
// c/a=2 c/b=2 二次変換 (a,b 非整数 |z|>1 は前で処理)
// 入力値z= 1.4 近辺で最小値-4.7程度になり入力値が大きくなるとゼロに近づく
if not aeqb(a, zeroc) then begin
c := cbiground(c, dpcs);
a := cbiground(a, dpcs);
ap := cdiv(c, a);
end;
if not aeqb(b, zeroc) then begin
c := cbiground(c, dpcs);
b := cbiground(b, dpcs);
bp := cdiv(c, b);
end;
if (checkbox2.Checked = true) and (ap.r = two) and (ap.i = zero) and (bp.r = two) and (bp.i = zero)
and not aeqb(z, onec) then begin
zback := z; // z=zback
one := one.RoundToPrecision(dpcs);
two := two.RoundToPrecision(dpcs);
tmf := one / two; // 1/2
c := caddb(b, tmf); // c = b + 1/2
aback := a; // a=>aback
a := cbiground(a, dpcs);
a := cdivb(a, two); // a = a/2
b := csub(b, a); // b = b - a/2
tmc := cmulb(z, four); // 4z
tmc := csubb(tmc, four); // 4z - 4
z := cbiground(z, dpcs);
tmc := cbiground(tmc, dpcs);
tmc := cdiv(z, tmc); // z / (4z-4)
z := cmul(tmc, z); // z^2 /(4z-4)
memo1.Lines.Append('c/a=2 c/b=2');
tmf := z.r.RoundToPrecision(40);
memo1.Lines.Append(ZeroErase('z= z^2 /(4z-4)= ' + tmf.ToString));
tmf := '0.9';
if zback.r > tmf then DS := 64 // z.re > 0.9 入力値z 1.16~7.6の時 1-1/z計算
else DS := 8; // z.re <=0.9
absz := cabs(z, dpcs); // |z|
tmf := absz.RoundToPrecision(40);
memo1.Lines.Append(ZeroErase('|z| = ' + tmf.ToString));
// 入力値 z
// 0.9 < /z/ < 2.2
d1 := '0.9';
d2 := '2.2';
if (absz > d1) and (absz < d2) and (z.r > zero) and (z.i = zero) and (DS <> 8) then begin
Hypergeometric_function_of_first_kind_aeb(a, b, c, z, eps, ans, n, f);
memo1.Lines.Append('変換 (1-1/z 0.9<|z|<2.2 Δ無し)');
goto TN0E;
end
else
goto ZG03; // Pfafの変換無し
end;
ZG02:
//--------------------------------------------------------------------------
// Pfaffの変換公式
// a = b c / a = 2 c / b = 2 の時はpfaff使用しない(許可設定あり
// Γ計算の都合上の±Δ計算の誤差が無ければ使用しても問題なし)
// zの実数部がゼロの時で/z/=1ならPfafの変換使用
// |z|>=1 IM(z)=0の場合計算結果に虚数部がある場合虚数部±が逆になる場合があるので注意
// 1近傍は1-1/z の線形接続公式を使用
// 0,75<|z|<=1 又は 1<|z|<2 a,b,c 小数部0 虚数部0
// zの虚数部の値によりPfaffを使用しない方が良い場合があります|z|=1近辺
ap.r := a.r.Frac; // re(a) 小数部
bp.r := b.r.Frac; // re(b) 小数部
cp.r := c.r.Frac; // re(c) 小数部
dnine := '0.75';
// 0,75<|z|<=1
if ((absz > dnine) and (absz <= one)) or
// 又は 1<|z|<2 re(a),re(b),re(c)の小数部0 im(a),im(b),im(c)虚数部0
((absz > one) and (absz < two) and (ap.r = zero) and (bp.r = zero) and (cp.r = zero)
and (a.i = zero) and (b.i = 0) and (c.i = 0)) then begin
// Pfaff変換範囲確認
PAFF := true;
d1 := '0.45';
d2 := '0.55';
if (z.r > d1) and (z.r < d2) then begin
PAFF := false;
tmc := csub(z, onec);
zbackp := cbiground(z, dpcs); // z-1
tmc := cbiground(tmc, dpcs);
zbackp := cdiv(zbackp, tmc); // z = z/(z-1)
nabsz := cabs(zbackp, dpcs); // |z|
end;
if (absz < one) and (nabsz < absz) then PAFF := true;
if (absz < one) and (nabsz > three) then PAFF := true;
if (absz > one) and (nabsz > absz) then PAFF := true;
// pfaff変換 有効 なら
if (checkbox3.Checked = true) and PAFF then begin
if not aeqb(a, zeroc) then begin
c := cbiground(c, dpcs);
a := cbiground(a, dpcs);
ap := cdiv(c, a); // c/a
end;
if not aeqb(bm, zeroc) then begin
c := cbiground(c, dpcs);
b := cbiground(b, dpcs);
bp := cdiv(c, b); // c/b
end;
// a,とbの実数部がc/2, zの虚数部が0でないなら
if (checkbox7.Checked = false) and (ap.r = two) and (bp.r = two) and (z.i = zero) then
else begin
am := csub(a, b); // a-b
cp := csub(c, b); // c-b
// |z| < 0.75 {z| < 2 z<>1 なら Pfafの変換
if (absz > dnine) and (absz <= two) and not aeqb(z, onec) then begin
// a=b c=a+1 c=b+1 でないなら 例 2,2,3 3,3,4でない
// c-b=1がcとbの値によって桁落ちするので cp=1 を not cp.re<1<cp.re で代用
if not (aeqb(am, zeroc) and not (aeqb(am, zeroc) and ((cp.r < one) or (cp.r > one)))) then begin
zbackP := z;
DS := DS or 4; // 4 pfaff 変換フラグセット
tmc := csub(z, onec); // z - 1
z := cbiground(z, dpcs);
tmc := cbiground(tmc, dpcs);
z := cdiv(z, tmc); // z = z/(z-1);
absz := cabs(z, dpcs); // |z|
b := csub(c, b); // b = c - b
end;
// a=b c=a+1 c=b+1 の時変換後aにΔ値加減算して近似計算
// 例 2,2,3 3,3,4 なら
if (aeqb(am, zeroc) and not ((cp.r < one) or (cp.r > one))) then begin
zbackP := (z);
DS := DS or 4 or 128; // 4 pfaff 変換フラグセット 128 は近似計算フラグ
tmc := csub(z, onec); // z - 1
z := cbiground(z, dpcs);
tmc := cbiground(tmc, dpcs);
z := cdiv(z, tmc); // z = z/(z-1);
absz := cabs(z, dpcs); // |z|
b := csub(c, b); // b = c - b
XLE := true;
end;
end;
end;
end;
end
else begin
// 1<|z|<2 の範囲は1-1/z計算使用
// z.re < 0 時は 1/z使用
ap := cadd(a, b); // a+b
ap := csub(ap, c); // a+b-c
am := csub(c, a); // c-a
am := csub(am, b); // c-a-b
if (checkbox2.Checked = true)
// a+b-c c-a-b c
and not zeroorounderbig(ap) and not zeroorounderbig(am) and not zeroorounderbig(c) then begin
d1 := '0.6';
ap := cadd(ap, onec); // a+b-c+1
am := cadd(am, onec); // c-a-b+1
// a+b-c+1 c-a-b+1 |z| > 1
if not zeroorounderbig(ap) and not zeroorounderbig(am) and (absz > one)
// /z/<2 RE(z) > 0
and (absz < two) and (z.r > d1) then begin
Hypergeometric_function_of_first_kind_aeb(a, b, c, z, eps, ans, n, f);
memo1.Lines.Append('変換 1-1/z 1<z<2 Δ無し計算');
goto TN0E;
end;
end;
end;
ZG03:
//--------------------------------------------------------------------------
// |z| > 1
// Γ値の値が±∞になる場合、微小値Δを加減算して計算平均値を答えにしています。
// a=bの計算の時は、aのみ微小値Δを加減算 a=bとa<>bでは、平均値の計算が違います。
if absz > one then begin // |z|が1より大きかったら
if (DS = 0) or (DS = 4) then XLE := false;
amb := csub(a, b);
bma := csub(b, a);
cma := csub(c, a);
cmb := csub(c, b);
aeb := csub(a, b);
df := 0;
// amb= 0 cma整数>0 又は 近似計算フラグ時 a±Δ近似値計算フラグセット df = 16
// aebフラグ1 (a±Δによりa=bではなくなります)
if (aeqb(amb, zeroc) and not zeroorounderbig(cma)) or (DS and 16 = 16) or (DS and 128 = 128) then
begin // DS=16 (a, b=a+1, b+1 b)
df := 16; // aのみΔ加算減算計算
aeb := onec; // df=16時はa±Δで計算する為 aeb では無くなります
end;
// 1/zの線接続公式の時±無限大になるΓ検出
if (df = 16) then
else begin
if zeroorounderbig(amb) then df := df or 1;
if zeroorounderbig(bma) then df := df or 2;
if zeroorounderbig(cma) then df := df or 4;
if zeroorounderbig(cmb) then df := df or 8;
end;
// 片側のΓ計算の分子と分母に一つの|∞|になるので±Δなし
if (df = 6) or (df = 9) or (df = 15) then begin
Hypergeometric_function_of_NO_delt(a, b, c, z, eps, ans, n, f);
if f <> 128 then begin
memo1.Lines.Append(' 1/z Δ無し計算 Γ/Γ');
XLE := false;
goto TN0E;
end;
f := 0;
end;
// Γ計算分母が無限大になる場合±Δなし
if (df and 12<> 0) and (df and 3 = 0) then begin
Hypergeometric_function_of_NO_delt(a, b, c, z, eps, ans, n, f);
if f <> 128 then begin
memo1.Lines.Append(' 1/z Δ無し計算 Γ/∞');
XLE := false;
goto TN0E;
end;
f := 0;
end;
// 両側のΓ計算の分母に|∞|片側の分子が|∞|になるので、a±Δの計算
if (df = 13) or (df = 14) then begin
df := 16;
aeb := onec; // df=16時はa±Δで計算する為 aeb では無くなります
end;
// |z| > 1 計算で Γ値が+∞-∞になるなら近似計算 Δα値を加算減算して計算し平均値を求めます
if checkbox1.Checked = true then begin
// a=bでΓ計算の分子が∞になり、分母に無限大がない場合計算結果が無限大になってしまうが、
// 実際には無限大ではないので、正解に近いΔ値を与えます。
if aeqb(amb, zeroc) then d1 := '2.8E-19'
else d1 := '1E-60';
if DS and 128 = 128 then d1 := '1.8E-19';
if deltbox.Checked = true then d1 := delt;
if aeqb(amb, zeroc) then DS:= DS or 128; // a=b の時は近似計算表示フラグセット
if df <> 0 then begin // 微小値のΔ加算減算が必用なら
XLE := true; // df > 0 近似計算表示選択 XLE = true
// a,b,cの何処にΔ補正するか選択
if (df = 1) or (df = 6) then df := 16; // a
if (df = 2) or (df = 9) then df := 32; // b
if (df = 4) or (df = 8) then df := 64; // c
// +Δ 計算
ap := a;
bp := b;
cp := c;
if df = 16 then ap := caddb(a, d1);
if df = 32 then bp := caddb(b, d1);
if df = 64 then cp := caddb(c, d1);
amb := csub(ap, bp);
bma := csub(bp, ap);
cma := csub(cp, ap);
cmb := csub(cp, bp);
Hypergeometric_function_of_first_kind(ap, bp, cp, amb, bma, cma, cmb, aeb, z, eps, tmc, n1, f); // Δ加算計算
// -Δ 計算
am := a;
bm := b;
cm := c;
if df = 16 then am := csubb(a, d1);
if df = 32 then bm := csubb(b, d1);
if df = 64 then cm := csubb(c, d1);
amb := csub(am, bm);
bma := csub(bm, am);
cma := csub(cm, am);
cmb := csub(cm, bm);
Hypergeometric_function_of_first_kind(am, bm, cm, amb, bma, cma, cmb, aeb, z, eps, ans, n2, f); // Δ減算計算
if n1 >= n2 then n := n1
else n := n2;
ans := cadd(ans, tmc);
ans := cbiground(ans, dpcs);
two := two.RoundToPrecision(dpcs);
ans := cdivb(ans, two); // 平均値
if df = 16 then memo1.Lines.Append(' 1/z a ±Δ 計算');
if df = 32 then memo1.Lines.Append(' 1/z b ±Δ 計算');
if df = 64 then memo1.Lines.Append(' 1/z c ±Δ 計算');
end
else begin // 微小値のΔ加算減算が必用 ないなら
Hypergeometric_function_of_NO_delt(a, b, c, z, eps, ans, n, f);
// Hypergeometric_function_of_first_kind(a, b, c, amb, bma, cma, cmb, aeb, z, eps, ans, n, f); // Δ無し
memo1.Lines.Append(' 1/z Δ=0 計算');
XLE := false;
end;
end
else begin // 無限大回避のチェックを外すと使用されます
Hypergeometric_function_of_NO_delt(a, b, c, z, eps, ans, n, f);
memo1.Lines.Append(' 1/z Δ無し計算');
XLE := false;
end;
end
else
if not aeqb(z, onec) then begin // z < 1 通常の超幾何関数計算
Hypergeometric_functionbig(a, b, c, z, eps, ans, n, f);
memo1.Lines.Append(' z < 1 ±Δ無し');
XLE := false;
end;
end; // TN=0 end
TN0E:
//----------------------------------------------------------------------------
if TN = 0 then begin // 通常計算
tmf := cabs(zback, dpcs);
tmf := tmf.RoundToPrecision(30);
memo1.Lines.Append(' |z| = ' + ZeroErase(tmf.ToString));
if f <> 8 then begin
tmf := cabs(z, dpcs);
tmf := tmf.RoundToPrecision(30);
memo1.Lines.Append('|new z| = ' + ZeroErase(tmf.ToString));
end;
end;
//----------------------------------------------------------------------------
if TN = 1 then begin // arctan計算
mz2 := cmul(z, z);
mz2 := cchs(mz2);
if absz > one then begin // zが1より大きかったら
amb := csub(a, b);
bma := csub(b, a);
cma := csub(c, a);
cmb := csub(c, b);
Hypergeometric_function_of_first_kind(a, b, c, amb, bma, cma, cmb, amb, mz2, eps, ans, n, f);
end
else // zが1より小さかったら
Hypergeometric_functionbig(a, b, c, mz2, eps, ans, n, f);
end;
//----------------------------------------------------------------------------
if TN = 2 then begin // arcsin計算
if az <> one then begin
mz2 := cmul(z, z);
Hypergeometric_functionbig(a, b, c, mz2, eps, ans, n, f);
end;
end;
//----------------------------------------------------------------------------
if BR or BRB or (n >= NC) then begin
tmc := ans;
epsback := epsback.RoundToPrecision(20);
epslimit(tmc, epsback.ToString);
end;
if BR then begin
memo1.Lines.Append('計算が途中で打ち切られました。');
if EpslimitF then
memo1.Lines.Append('計算結果は正しくありません。')
else
memo1.Lines.Append('近似値を表示します。');
end;
if n >= maxloops then begin
memo1.Lines.Append('計算が' + intTostr(maxloops) + 'Loopで収束しませんでした。');
if EpslimitF then
memo1.Lines.Append('計算結果は正しくありません。')
else
memo1.Lines.Append('計算結果は正しくありません、近似値を表示します。');
if DS and 4 = 4 then
memo1.Lines.Append('Pfaff変換のチェックを外すと収束する可能性があります。');
end
else begin
if TN = 0 then begin // 通常計算
memo1.Lines.Append('ガウスの超幾何関数');
end;
end;
// ∞表示
if (f = 1) or (f = -1) then begin
if ans.r >= zero then memo1.Lines.Append('∞')
else memo1.Lines.Append('-∞');
if ans.i > zero then memo1.Lines.Append('+∞i');
if ans.i < zero then memo1.Lines.Append('-∞i');
end;
// Z>1 計算時Γ計算が無限大になる場合 f=128
if f = 128 then begin
memo1.Lines.Append('Γ計算が+∞あるいは-∞になりました。');
memo1.Lines.Append('無限大回避にチェックを入れてください。');
goto EXT;
end;
//----------------------------------------------------------------------------
if TN = 0 then begin // 通常計算
// 絶対値が指定値より小さかったら0セット
if (f = 16) or (f = -2) then begin
memo1.Lines.Append('演算不可');
memo1.Lines.Append('無限大回避にチェックを入れてください。');
goto EXT;
end;
if XLE and not EpslimitF then
memo1.Lines.Append(' 極限計算');
// z=1 計算 ∞時
if f = 8 then begin
memo1.Lines.Append('z = 1');
memo1.Lines.Append(' Re(c - a - b) <= 0');
if ans.r >= zero then memo1.Lines.Append(' ∞')
else memo1.Lines.Append('-∞');
if ans.i > zero then memo1.Lines.Append('+∞i');
if ans.i < zero then memo1.Lines.Append('-∞i');
goto EXT;
end;
// pfaff変時出力設定
if DS and 4 = 4 then begin
tmc := csub(onec, zbackp); // 1-z
ap := cchs(a); // -a
tmc := pow_big(tmc, ap, epsln); // (1-z)^-a
ans := cmul(ans, tmc); // ans = ans * ((1-z)^-a)
tmf := cabs(zbackp, dpcs);
memo1.Lines.Append(' Pfaff');
// re(z) > 1 im(z)=0 の時 虚数部の符号が反転するので修正します。
if (zbackp.r > one) and (zbackp.i = zero) then ans.i := - ans.i;
end;
// 二次 z^2/(z^2/(z4-4)) 変換時出力 必ずpfaffの後に実行
if (DS and 8 = 8) or (DS and 64 = 64) then begin
tmc := csub(onec, zback); // 1-z
aback := cchs(aback); // -a
aback := cbiground(aback, dpcs);
two := two.RoundToPrecision(dpcs);
aback := cdivb(aback, two); // -a/2
tmc := pow_big(tmc, aback, epsln); // (1-z)^-a/2
ans := cmul(ans, tmc); // ans = ans * ((1-z)^-a/2)
memo1.Lines.Append(' F(a=b c=2b, z^2/(z4-4)');
end;
if BR or BRB or (n >= NC) then
else
if abs(f) <> 1 then begin
memo1.Lines.Append('(最大60桁表示)');
tmf := ans.r.RoundToPrecision(60);
memo1.Lines.Append(' (' + ZeroErase(tmf.ToString) + ')');
tmf := ans.i.RoundToPrecision(60);
memo1.Lines.Append(' (' + ZeroErase(tmf.ToString) + ' i)');
end;
// 近似計算時ゼロ設定
if XLE and not (deltbox.Checked = true) then begin
if (DS and 32 = 32) or (DS and 128 = 128) then
zerounde1em35(ans) // 1E-35以下ゼロ設定
else
zerounde1em42(ans); // 1E-42以下ゼロ設定
end
else
zerounde1em52(ans); // 1E-52以下ゼロ設定
if BR or BRB or (n >= NC) then
epslimit(ans, epsback.ToString) // 収束値による表示制限
else
epslimit(ans, epsedit.Text); // 収束判定値による表示制限
// 計算結果表示 近似計算時は40桁 通常は50桁表示 a=b でpfaff時は35桁表示
if (f = 0) or (f = 4) or (f = 16) then begin
memo1.Lines.Append('ans');
az := ans.r.Abs;
if az > infs then begin
if ans.r > zero then memo1.Lines.Append(' ∞')
else memo1.Lines.Append(' -∞');
end
else begin
if XLE and ((DS and 32 = 32) or (DS and 128 = 128)) and not (deltbox.Checked = true) then begin
memo1.Lines.Append(' 精度が低くなっています。');
end;
if deltbox.Checked = true then begin
d1 := '1e-40';
d2 := '1e-100';
if ((delt > d1) or (eps > d2)) and (absz > one) then
memo1.Lines.Append(' 近似値表示 ')
end;
if XLE and not (deltbox.Checked = true) then begin
if (DS and 32 = 32) or (DS and 128 = 128) then begin
tmf := ans.r.RoundToPrecision(33);
if tmf.Abs > epsln then
memo1.Lines.Append(' ' + ZeroErase(tmf.ToString))
else
memo1.Lines.Append(' ' + '0.0');
end
else begin
tmf := ans.r.RoundToPrecision(40);
if tmf.Abs > epsln then
memo1.Lines.Append(' ' + ZeroErase(tmf.ToString))
else
memo1.Lines.Append(' ' + '0.0');
end;
end
else begin
tmf := ans.r.RoundToPrecision(50);
if tmf.Abs > epsln then
memo1.Lines.Append(' ' + ZeroErase(tmf.ToString))
else
memo1.Lines.Append(' ' + '0.0');
end;
end;
az := ans.i.Abs;
if az > infs then begin
if ans.i > zero then memo1.Lines.Append(' +∞i')
else memo1.Lines.Append(' -∞i');
end
else begin
if XLE and not (deltbox.Checked = true) then begin
if (DS and 32 = 32) or (DS and 128 = 128) then begin
tmf := ans.i.RoundToPrecision(33);
if tmf.Abs > epsln then
memo1.Lines.Append(' ' + ZeroErase(tmf.ToString) + ' i')
else
memo1.Lines.Append(' ' + '0.0' + ' i');
end
else begin
tmf := ans.i.RoundToPrecision(40);
if tmf.Abs > epsln then
memo1.Lines.Append(' ' + ZeroErase(tmf.ToString) + ' i')
else
memo1.Lines.Append(' ' + '0.0' + ' i');
end
end
else begin
tmf := ans.i.RoundToPrecision(50);
if tmf.Abs > epsln then
memo1.Lines.Append(' ' + ZeroErase(tmf.ToString) + ' i')
else
memo1.Lines.Append(' ' + '0.0' + ' i');
end;
end;
end;
end;
//----------------------------------------------------------------------------
if TN = 1 then begin // arctan計算
tans := cmul(ans, z); // z *
if DS = 1 then
memo1.Lines.Append('arctan(z) rad 超幾何関数計算');
if DS = 2 then
memo1.Lines.Append('arcsin(z) rad 超幾何関数計算');
tmf := tans.r.RoundToPrecision(50);
memo1.Lines.Append(ZeroErase(' ' + tmf.ToString));
tmf := arctana_bigf(z.r, paib, dpcs);
tmf := tmf.RoundToPrecision(50);
memo1.Lines.Append('rad 組込み関数計算');
memo1.Lines.Append(ZeroErase(' ' + tmf.ToString));
end;
//----------------------------------------------------------------------------
if TN = 2 then begin // arcsin計算
if az <> one then
tans := cmul(ans, z) // z *
else begin
ans.r := paib;
tans.r := tans.r.RoundToPrecision(dpcs);
two := two.RoundToPrecision(dpcs);
tans.r := tans.r / two;
tans := cmul(tans, z) // z *
end;
if DS = 1 then
memo1.Lines.Append('arctan(z) rad 超幾何関数計算');
if DS = 2 then
memo1.Lines.Append('arcsin(z) rad 超幾何関数計算');
tmf := tans.r.RoundToPrecision(50);
memo1.Lines.Append(ZeroErase(' ' + tmf.ToString));
memo1.Lines.Append('rad 組込み関数計算');
tmf := arcsina_big(z.r, dpcs);
tmf := tans.r.RoundToPrecision(50);
memo1.Lines.Append(ZeroErase(' ' + tmf.ToString));
end;
EXT:
button1.Enabled := True;
TN := 0; // artn arsin 解除
DS := 0; // artn arsin pfaff 二次変換 近似計算 解除
end;
//------------------------------------------------------------------------------
// 初期設定
procedure TForm1.FormCreate(Sender: TObject);
begin
BigDecimal.DefaultPrecision := DPS;
epsb := EPSC;
precisionedit.Text := intTostr(DPS);
memo1.Clear;
Label1.Caption := ' 設定値によって、中々収束しません。' + #13#10 +
'その時は計算打切りボタンで停止して' + #13#10 +
'下さい。';
Label2.Caption := ' RE(z)≒0.5 |z|≒1は中々収束しません、収束判定値を' + #13#10 +
'大きくすれば精度は悪くなり表示桁数は少なくなりますが、' + #13#10 +
'計算は早く終了します。 例 1e-20, 1e-50';
BR := false;
TN := 0; // 計算実行 0 通常 1 artan 2 arsin
DS := 0; // 計算表示 0 通常 1 artan 2 arsin 4 pfaff 8,64 二次変換 32,128 近似計算
maxloops := NC;
disploops := NC div 200;
maxloopedit.Text := inttostr(NC div 10000);
// 0,1,2,3,4, π
zero := bigdecimal.Zero;
one := bigdecimal.One;
two := bigdecimal.Two;
three := two + one;
four := two + two;
// ガンマ計算∞設定値
maxmpfbig := '1.0e+1000000'; // 有効桁数 255桁 演算最大値 ガンマ計算時最大値
// ガンマ値にこれより大きい値を与えると演算が
// 出来なくなります。
// ∞判別値
infs := '1.0e+100000'; // 演算結果が之より大きい時無限大判定
// ベルヌーイ数分母分子配列表作成
Bernoulli_number_BigInteger;
comment;
end;
// close時 多倍長配列解放
procedure TForm1.FormCloseQuery(Sender: TObject; var CanClose: Boolean);
begin
// 演算中 close禁止
if not button1.Enabled then CanClose := false;
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
comment;
end;
procedure TForm1.epsEditChange(Sender: TObject);
begin
Z10F := false;
end;
end.
複素数演算用pas
このpasの中に、arctanがあるのですが、arg(複素数の角度)にしか利用されていないので、実数の計算となっています。
arctanは超幾何関数でも計算が出来るのですが、プログラムが煩雑になるので、別途用意しました。
Big_complex.pas
unit Big_complex;
interface
uses system.Math, Velthuis.BigIntegers, Velthuis.Bigdecimals;
// 複素数構造体
type
CBig = record
r : bigdecimal;
i : bigdecimal;
end;
function cadd(a, b: CBig): CBig;
function csub(a, b: CBig): CBig;
function cmul(a, b: Cbig): CBig;
function cdiv(a, b: Cbig): Cbig;
function caddb(a: cbig; b: bigdecimal): cbig;
function csubb(a: cbig; b: bigdecimal): cbig;
function cmulb(a: Cbig; b: bigdecimal): CBig;
function cdivb(a: Cbig; b: bigdecimal): Cbig;
function cabs(a : cbig; dpcs : integer): bigdecimal;
function exp_big(x: Cbig; dpcs: integer; eps : bigdecimal): Cbig;
function pi_big: Bigdecimal;
function log_big(z : Cbig; eps : bigdecimal; dpcs: integer): Cbig;
function sin_big(z : Cbig; eps : bigdecimal; dpcs: integer): Cbig;
function cbiground(x : cbig; dpcs : integer): cbig;
function aeqb(x, y : cbig): boolean;
function pow_big(x, y : cbig; eps : bigdecimal): cbig;
function cchs(x: cbig): cbig;
function arctana_bigf(xi, pib: bigdecimal; dpcs: integer): bigdecimal;
function arcsina_big(xi: bigdecimal; dpcs : integer): bigdecimal;
function arg_big(z : cbig): bigdecimal;
implementation
uses main;
// cbig = -cbig
function cchs(x: cbig): cbig;
begin
result.r := -x.r;
result.i := -x.i;
end;
// CBig複素数の加算
function cadd(a, b: CBig): CBig;
begin
result.r := a.r + b.r;
result.i := a.i + b.i;
end;
// CBig複素数の減算
function csub(a, b: CBig): CBig;
begin
result.r := a.r - b.r;
result.i := a.i - b.i;
end;
// cbig + bigdecimal
function caddb(a: cbig; b:bigdecimal): cbig;
begin
result.r := a.r + b;
result.i := a.i;
end;
// cbig - bigdecimal
function csubb(a : cbig; b: bigdecimal): cbig;
begin
result.r := a.r - b;
result.i := a.i;
end;
// Cbig bigdecimalの乗算
function cmulb(a: Cbig; b: bigdecimal): CBig;
begin
result.r := a.r * b;
result.i := a.i * b;
end;
// Cbig複素数の乗算
function cmul(a, b: Cbig): CBig;
begin
result.r := a.r * b.r - a.i * b.i;
result.i := a.r * b.i + a.i * b.r;
result := cbiground(result, DPS);
end;
// Cbig bigdecimalの除算
function cdivb(a: Cbig; b: bigdecimal): Cbig;
begin
if b <> Bigdecimal.Zero then begin
result.r := a.r / b;
result.i := a.i / b;
end
else begin
result.r := Bigdecimal.Zero;
result.i := Bigdecimal.Zero;
end;
end;
// Cbig複素数の除算
function cdiv(a, b: Cbig): Cbig;
var
bb, arbraibi, aibrarbi: Bigdecimal;
begin
bb := b.r * b.r + b.i * b.i;
arbraibi := a.r * b.r + a.i * b.i;
aibrarbi := a.i * b.r - a.r * b.i;
bb := bb.RoundToPrecision(DPS);
arbraibi := arbraibi.RoundToPrecision(DPS);
aibrarbi := aibrarbi.RoundToPrecision(DPS);
if bb <> Bigdecimal.Zero then begin
result.r := arbraibi / bb;
result.i := aibrarbi / bb;
end
else begin
result.r := Bigdecimal.Zero;
result.i := Bigdecimal.Zero;
end;
end;
// x: cbig dpcs桁に丸め
function cbiground(x : cbig; dpcs : integer): cbig;
begin
result.r := x.r.RoundToPrecision(dpcs);
result.i := x.i.RoundToPrecision(dpcs);
end;
// a:cbig = b:cbig
function aeqb(x, y : cbig): boolean;
begin
if (x.r = y.r) and (x.i = y.i) then result := true
else result := false;
end;
// Cbigの絶対値
function cabs(a : cbig; dpcs : integer): bigdecimal;
var
arh2, aih2 : bigdecimal;
tmp : bigdecimal;
begin
arh2 := a.r * a.r;
aih2 := a.i * a.i;
arh2 := arh2.RoundToPrecision(dpcs);
aih2 := aih2.RoundToPrecision(dpcs);
tmp := arh2 + aih2;
result := bigdecimal.Sqrt(tmp, dpcs);
end;
// exp(x)
// x 入力値 複素数
// dpcs 有効桁数
// eps 収束判定値
function exp_big(x: Cbig; dpcs: integer; eps : bigdecimal): Cbig;
var
xh, s, sb, si, ss: Cbig;
one, ass, eight, i, ih : bigdecimal;
begin
one := bigdecimal.One;
eight := bigdecimal.Ten - bigdecimal.Two;
eight := eight.RoundToPrecision(dpcs);
x.r := x.r.RoundToPrecision(dpcs);
x.i := x.i.RoundToPrecision(dpcs);
x.r := x.r / eight;
x.i := x.i / eight;
i := one;
ih := i;
xh := x;
s := x;
repeat
sb := s;
i := i + one;
ih := ih * i; // i!
xh := cmul(xh, x); // x^n
xh.r := xh.r.RoundToPrecision(dpcs);
xh.i := xh.i.RoundToPrecision(dpcs);
si := cdivb(xh, ih); // x^n/i!
s := cadd(s, si);
ss := csub(s, sb);
ass := cabs(ss, dpcs);
until (ass < eps);
s.r := s.r + one;
s := cmul(s, s);
s := cmul(s, s);
result := cmul(s, s);
result.r := result.r.RoundToPrecision(dpcs);
result.i := result.i.RoundToPrecision(dpcs);
end;
// π
function pi_big: Bigdecimal;
var
n, dpcs, dpcsback : integer;
rmback : BigDecimal.RoundingMode;
SQRT_SQRT_EPSILON, c, b, e : BigDecimal;
npow : Bigdecimal;
a, one, two, four, five, eight : Bigdecimal;
begin
rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ
dpcsback := BigDecimal.DefaultPrecision;
dpcs := dpcsback + 5; // 指定精度 + α
BigDecimal.DefaultPrecision := dpcs;
BigDecimal.DefaultRoundingMode := rmNearesteven;
one := '1';
one := one.RoundToPrecision(dpcs); // oneの有効桁数をdpcsに設定
two := '2';
four := '4';
five := '5';
eight := '8';
SQRT_SQRT_EPSILON := one / BigDecimal.IntPower(two, dpcs shl 0); // 収束判定値
c := BigDecimal.Sqrt(one / eight, dpcs * 2);
a := one + c + c + c;
b := BigDecimal.Sqrt(a, dpcs * 2);
e := b - five / eight;
b := b + b;
c := e - c;
a := a + e;
npow := '4';
n := 0;
while (e > SQRT_SQRT_EPSILON) and (n < 100) do begin
npow := npow + npow;
e := (a + b) / two; // 平均値 除算有効桁数での丸め
b := a * b;
b := b.RoundToPrecision(dpcs); // pcs + α 丸め
b := BigDecimal.Sqrt(b, dpcs * 2); // 平方根有効桁数での丸め
e := e - b;
b := b + b;
c := c - e;
a := e + b;
inc(n);
end;
e := e * e;
e := e.RoundToPrecision(dpcs); // pcs + α 丸め
e := e / four; // e = e * e / 4
a := a + b;
result := (a * a - e - e / two) / (a * c - e) / npow; // 除算の順番に注意
result := result.RoundToPrecision(dpcsback); // 指定の精度に丸め
BigDecimal.DefaultPrecision := dpcsback; // 除算演算精度復帰
BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰
end;
// z 入力値 複素数
// eps 収束判定値
// dpcs 有効桁数
// ndis 収束表示 true 表示 false 非表示
function log_big_sub(z : Cbig; eps : bigdecimal; dpcs: integer; ndis: boolean): Cbig;
const
NN = 1000000;
var
s, x, zm1, zp1, xh2, xg, n2p1 : CBig;
one, two : Cbig;
xgsn : Cbig;
asabs : bigdecimal;
n : integer;
begin
one.r := Bigdecimal.One; // 1
one.i := Bigdecimal.Zero; //
two := cadd(one, one); // 2
zm1 := csub(z, one); // z - 1
zp1 := cadd(z, one); // z + 1
x := cdiv(zm1, zp1); // x = (z-1)/(z+1)
s.r := Bigdecimal.Zero;
s.i := Bigdecimal.Zero;
xh2 := cmul(x, x); // x^2
xg := x; // n = 0; x^(2n+1)
n2p1 := one; // 2n+1 = 1
n := 0;
repeat
xg.r := xg.r.RoundToPrecision(dpcs);
xg.i := xg.i.RoundToPrecision(dpcs);
xgsn := cdiv(xg, n2p1); // x^(2n+1) / (2n+1)
s := cadd(s, xgsn); // Σ
xg := cmul(xg, xh2); // x^(2n+1)
n2p1 := cadd(n2p1, two); // 2n + 1
inc(n);
asabs := cabs(xgsn, dpcs);
until (asabs < eps) or (n > NN);
s := cmul(s, two);
result := s;
end;
// z 因数
// eps 収束判定値
// dpcs 有効桁数
// 返り値 対数複素数
function log_big(z : Cbig; eps : bigdecimal; dpcs: integer): Cbig;
var
zb : Cbig;
z10n : cbig;
Zmax, ten, one, bn : bigdecimal;
pi_big2: bigdecimal;
begin
if (z.r = bigdecimal.Zero) and (z.i = bigdecimal.Zero) then begin
result.r := bigdecimal.Zero;
result.i := bigdecimal.Zero;
exit;
end;
pi_big2 := paib / bigdecimal.Two; // paib = pi_bigs main.pas
zb := z;
// 虚数と実数両方ともゼロでないなら 実数部側を大きな値にして演算誤差を小さくします
if (zb.r <> bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin
if zb.i.Abs(zb.i) > zb.r.Abs(zb.r) then begin // 虚数の絶対値が実数の絶対値より大きい時入れ替え
z.r := zb.i;
z.i := zb.r;
if zb.i < bigdecimal.Zero then begin // 虚数が負数だったら符号反転
z.r := -z.r;
z.i := -z.i;
end;
end
else begin // 虚数の絶対値が実数の絶対値と等しいか小さい時
if zb.r < bigdecimal.Zero then begin // 実数の値が負数だったら符号反転
z.r := -zb.r;
z.i := -zb.i;
end;
end;
end;
// z.rが0でz.iがゼロでない時 虚数部と実数部入れ替え
if (zb.r = bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin
z.r := zb.i;
z.i := zb.r;
if z.r < bigdecimal.Zero then z.r := -z.r; // 実数部が負数だったら符号反転 虚数部ゼロなのでそのまま
end;
// 実数部が負数ので虚数部ゼロの時符号を反転 虚数部ゼロなのでそのまま
if (zb.r <> bigdecimal.Zero) and (zb.i = bigdecimal.Zero) then
if zb.r < bigdecimal.Zero then z.r := -zb.r;
// 10の対数を利用して大きな値の計算を速くします
ten := '10';
ten := ten.RoundToPrecision(dpcs); // dpcs桁合わせ
one := bigdecimal.One;
bn := bigdecimal.Zero;
if not Z10F then begin
z10.r := ten;
z10.i := bigdecimal.Zero;
z10 := log_big_sub(z10, eps, dpcs, false); // 10の対数
z10F := true;
end;
zmax := cabs(z, dpcs); // zの絶対値
zmax := zmax.RoundToPrecision(dpcs); // dpcs桁合わせ
z.r := z.r.RoundToPrecision(dpcs); // dpcs桁合わせ
z.i := z.i.RoundToPrecision(dpcs); // dpcs桁合わせ
// 10で除算又は乗算して値がの値が1~10の範囲に入るようにします。
repeat
if zmax > ten then begin // zmaxが10より大きい時10で除算
z.r := z.r / ten;
z.i := z.i / ten;
zmax := zmax / ten;
bn := bn + one; // 10で除算した回数 +になります。
end;
if zmax < one then begin // zmaxが1より小さい時10を乗算
z.r := z.r * ten;
z.i := z.i * ten;
zmax := zmax * ten;
bn := bn - one; // 10を乗算した回数 -になります。
end;
until (zmax <= ten) and (zmax >= one);
//----------------------------------------
// 修正された値で対数計算
result := log_big_sub(z, eps, dpcs, true);
// 10の対数補正
z10n.r := z10.r * bn; // 加算する対数値計算10の対数値のn倍
z10n.i := z10.i * bn;
result.r := result.r + z10n.r; // 10の対数値のn倍加算
result.i := result.i + z10n.i;
//----------------------------------------
// z.rがゼロでz.iがゼロでない時 虚数部π/2補正
if (zb.r = bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin
if zb.i >= bigdecimal.Zero then result.i := result.i + pi_big2
else result.i := result.i - pi_big2;
end;
// z.rの値が負数のきと符号を変更して計算しているの虚数部π補正。
if (zb.r < bigdecimal.Zero) and (zb.i = bigdecimal.Zero) then
result.i := result.i + pi_big;
// 虚数と実数両方ともゼロでない時
if (zb.r <> bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin
// 次数部絶対値より虚数部の絶対値が大きい場合
if zb.i.Abs(zb.i) > zb.r.Abs(zb.r) then begin
if zb.i > bigdecimal.Zero then result.i := -result.i + pi_big2 // π/2補正
else result.i := -result.i - pi_big2;
end
// 実数部が負数の時
else begin
if zb.r < bigdecimal.Zero then
if zb.i > bigdecimal.Zero then result.i := result.i + pi_big // π補正
else result.i := result.i - pi_big
end;
end;
end;
// arcsin
// 0.7を超えたら反対側の角度を求めます(arccos計算になります)
// arcsin(x) = π/2 - arccos(x)
function arcsina_big(xi: bigdecimal; dpcs : integer): bigdecimal;
label
EXT;
var
i : integer;
ans, bans, fa, fb, d, ab, ta, tb, f, x, seven, zero, one, two, ax: bigdecimal;
begin
dpcs := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ
xi := xi.RoundToPrecision(dpcs);
zero := bigdecimal.Zero;
seven := '0.7';
one := bigdecimal.One;
two := bigdecimal.Two;
i := 1;
fa := one;
x := BigDecimal.Abs(xi);
ax := x;
if ax = one then begin // 1だったらπ/2 90°
ans := paib / two;
goto EXT;
end;
if ax > seven then begin // 0.7を超えたらcosの計算
x := one - x * x;
x := x.RoundToPrecision(dpcs);
x := BigDecimal.Sqrt(x, dpcs * 2); // sqrt は有効桁数が1/2
end;
fb := two;
ta := fa;
tb := fb;
ab := '3';
d := x * x * x;
d := d.RoundToPrecision(dpcs);
ans := (x + d * (ta / tb / ab));
repeat
bans := ans;
d := d * x * x;
d := d.RoundToPrecision(dpcs);
fa := fa + two;
fb := fb + two;
ab := ab + two;
ta := ta * fa;
ta := ta.RoundToPrecision(dpcs);
tb := tb * fb;
tb := tb.RoundToPrecision(dpcs);
f := (ta / tb / ab) * d;
ans := ans + f;
inc(i);
until (bans = ans) or (i > 10000);
if ax > seven then ans := paib / two - ans;
EXT:
ans := ans.RoundToPrecision(dpcs);
if xi < zero then ans := -ans;
result := ans;
end;
// sin(z)
// eps 収束判定値
// dpcs 有効桁数
// 返り値 sin複素数
function sin_big(z : Cbig; eps : bigdecimal; dpcs: integer): Cbig;
var
zh2n1, zh2: cbig;
fa2n1, fn, one : bigdecimal;
s, sb, tmp : cbig;
abss: bigdecimal;
FG : boolean;
begin
// n = 0
one := bigdecimal.One;
zh2n1 := z; // z^(2n+1)
zh2 := cmul(z,z); // z^2
fa2n1 := one; // (2n+1)!
fn := one; // (2*0+1)!
s := z; // z
FG := false; // 次は奇数
// n = 1 ~
repeat
sb := s;
zh2n1 := cmul(zh2n1, zh2); // z^(2n+1) = z^(2n+1) * Z^2
fn := fn + one; // fn = fn + 1
fa2n1 := fa2n1* fn; // (2n+1)! = fa2n1*fn
fn := fn + one; // fn = fn + 1
fa2n1 := fa2n1* fn; // (2n+1)! = fa2n1*fn
// 除算前に桁揃え
fa2n1 := fa2n1.RoundToPrecision(dpcs);
zh2n1.r := zh2n1.r.RoundToPrecision(dpcs);
zh2n1.i := zh2n1.i.RoundToPrecision(dpcs);
tmp := cdivb(zh2n1, fa2n1); // z^(2n+1) / (2n+1)!
if FG then begin // 偶数なら
s := cadd(s, tmp); // 加算
FG := false; // 次は奇数
end
else begin // 奇数なら
s := csub(s, tmp); // 減算
FG := true; // 次は偶数
end;
abss := cabs(tmp, dpcs);
until abss < eps;
result := s;
end;
// x^y
// 実数、虚数部がゼロになる条件でも、演算誤差により、ゼロにならないのて、条件判定をして強制的
// にゼロにしています。
function pow_big(x, y : cbig; eps : bigdecimal): cbig;
var
dpcs : integer;
harf, absi, absy, four : bigdecimal;
lnx, tmp : cbig;
begin
if (x.r = bigdecimal.zero) and (x.i = bigdecimal.zero) then begin
result.r := bigdecimal.Zero;
result.i := bigdecimal.Zero;
exit;
end;
dpcs := BigDecimal.DefaultPrecision;
lnx := log_big(x, eps, dpcs); // ln(x)
lnx := cbiground(lnx, dpcs); // ppcs 丸め
y := cbiground(y, dpcs); // ppcs 丸め
tmp := cmul(lnx, y);
tmp := cbiground(tmp, dpcs); // ln(x) * y
result := exp_big(tmp, dpcs, eps);
// xの虚数部とyの虚数部0なら
if (x.i = bigdecimal.zero) and (y.i = bigdecimal.Zero) then begin
harf := bigdecimal.One / bigdecimal.Two; // 0.5
absy := y.r.Abs(y.r); // yの実数部の絶対値
absi := absy.Frac; // yの実数部の絶対値の小数部
absi := absi - harf; // yの実数部の絶対値の小数部と0.5の差分
// 差分がゼロ(yの実数部の小数部が0.5)
if absi = bigdecimal.Zero then
// xの実数部が0と等しいか0より大きいなら
if x.r >= bigdecimal.zero then result.i := bigdecimal.zero // 答えの虚数部0
// 0より小さいなら
else result.r := bigdecimal.zero; // 答えの実数部0
absi := y.r.Frac; // 乗数の小数部
if absi = bigdecimal.Zero then result.i := bigdecimal.Zero; // 整数なら答えの虚数部0
end;
// xの整数部とyの虚数部が0なら
if (x.r = bigdecimal.Zero) and (y.i = bigdecimal.Zero) then begin
absi := y.r.Frac; // 乗数の小数部
if absi = bigdecimal.Zero then begin // 整数なら
absy := y.r / bigdecimal.Two; // 偶数奇数確認
absi := absy.Frac; // 小数部
if absi = bigdecimal.Zero then result.i := bigdecimal.Zero // 偶数なら 虚数部0
else result.r := bigdecimal.Zero; // 奇数なら実数部0
end;
end;
absy := x.r.Abs(x.r); // |x.r|
absi := x.i.Abs(x.i); // |x.i|
// xの実数部と虚数部の絶対値が等しくてy.rがゼロでなかったら
if (absy = absi) and (y.i = bigdecimal.Zero) and not (y.r = bigdecimal.Zero) then begin
absi := y.r.Frac; // 乗数の小数部
if absi = bigdecimal.Zero then begin // 整数なら
absy := y.r / bigdecimal.Two; // 偶数奇数確認
absi := absy.Frac; // 小数部
if absi = bigdecimal.Zero then begin // 偶数なら
four := bigdecimal.Two + bigdecimal.Two; // 4
absy := y.r / four; // 4偶数奇数確認
absi := absy.Frac; // 小数部
if absi = bigdecimal.Zero then result.i := bigdecimal.Zero // 偶数なら 虚数部0 y= 4 8
else result.r := bigdecimal.Zero; // 奇数なら 実数部0 y= 2 6 10
end;
end;
end;
end;
// arctan
// 1 を越えたら反対側の角度を計算
// レオンハルト・オイラーの計算
function arctana_bigf(xi, pib: bigdecimal; dpcs: integer): bigdecimal;
var
i : integer;
x, ax, y, ans, bans, f, ib, zero, one, two, a2: bigdecimal;
begin
xi := xi.RoundToPrecision(dpcs);
x := bigdecimal.Abs(xi);
ax := x;
zero := '0';
one := '1';
two := '2';
if x > one then ax := one / x;
a2 := ax * ax;
a2 := a2.RoundToPrecision(dpcs);
y := a2 / (one + a2);
// y := y.RoundToScale(dpcs, rmNearesteven);
i := 0;
ib := one;
ans := one;
f := one;
repeat
bans := ans;
f := f * ib * (two / (ib * two + one)) * y;
f := f.RoundToPrecision(dpcs);
ans := ans + f;
ans := ans.RoundToPrecision(dpcs);
ib := ib + one;
inc(i);
until (bans = ans) or (i > 10000);
if ax <> zero then ans := ans * (y / ax)
else ans := zero;
if x > one then ans := pib / two - ans;
if xi < zero then ans := -ans;
result := ans;
end;
// 複素数偏角計算
function arg_big(z : cbig): bigdecimal;
var
zin : cbig;
x, y, ysx, pi1s2, zero : bigdecimal;
dpcs :integer;
begin
dpcs := BigDecimal.DefaultPrecision;
zero := bigdecimal.Zero;
zin := cbiground(z, dpcs);
result := zero;
x := zin.r;
y := zin.i;
if (x = zero) and (y = zero) then exit;
pi1s2 := paib / bigdecimal.two;
if (x = zero) and (y > zero) then result := pi1s2;
if (x = zero) and (y < zero) then result := - pi1s2;
if x <> zero then begin
ysx := y / x;
if x > zero then result := arctana_bigf(ysx, paib, dpcs);
if x < zero then begin
if y >= zero then result := arctana_bigf(ysx, paib, dpcs) + paib;
if y < zero then result := arctana_bigf(ysx, paib, dpcs) - paib;
end;
end;
end;
end.
 Gauss_hypergeometric_function_big.zip
Gauss_hypergeometric_function_big.zip
三角関数、逆三角関数、その他関数 に戻る
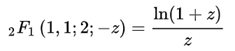
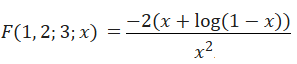 x<>1
x<>1