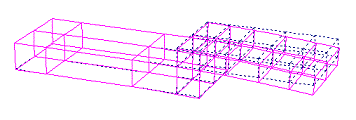
ソリッドモデル有限要素法（２０節点　アイソパラメトリック　共役勾配法）

　ソリッドモデル　２０節点　アイソパラメトリックによる有限要素法の計算プログラムについて。
DOSの時代に、参考書を元にソリッドモデルの有限要素法のプログラムを入力し、その後、入出力と、大撓みのルーチンを追加しました。
この頃の参考書のソリッドモデルのプログラムは殆どが、フォートランで、それ以外の言語のものはありませんでした、その頃のパソコンの性能では、データーの解析に無理があったからでしょう。
　この時代、マイクロソフトが、ＤＯＳ用のフォートランを供給していたので、それを使用してプログラムの確認をしましたが、計算できる要素の数は、最大約１００個程度で、本当に１００個の要素を計算すると、結果が出るのに１時間以上かり、十数個のデーターでも、１０分以上かかるような状態でした。
パソコンの性能は、飛躍的に向上し、現在は十分にソリッドモデルのデーター解析で実用に耐えられるようです。
　六面体２０節点アイソパラメトリック要素の場合、ガウスの積分点を５×５×５迄指定でき、計算点が可なりの数となるので、要素数が少なくても、精度の良い結果が出せます。
　使用できる要素数は約８００個程度ですが、構成条件によって、変化します。
現在のパソコンなら、配列の値を大きくすれば、もっと多い要素でも計算可能ですが、本プログラムは、形状要素の入力及び編集機能はあまり良くありません、単純な形状なら問題ありませんが、複雑な形状の入力は可なりの労力を要します。
　現在の編集機能では、大量の要素を扱うのには無理があるので、要素数８００程度で十分かと思います。
　プログラムは、メニュー、仮データーの作成、入力データーのチェック、微小撓み計算、応力計算指定、応力計算、大撓み計算、計算結果表示、の八個で構成されています。更に、ヘルプファイルもあり、ヘルプファイルは、コンパイル済みのと、ＨＴＭＬ　ＷＯＲＫ　ＳＨＯＰ用のソースリストが添付されています。
　全ての実行ファイルを同じフォルダーに入れて、メニューのショートカットをディスクトップに置けば、メニューから各プログラムの実行が可能です、同時に各ステップのプログラムを実行出来るので、計算することにあまりストレスは感じないでしよう。
あまり良くありませんが、一応取り扱い説明書に近いものも添付してありますし、サンプルも添付してあるので、参考にして下さい。

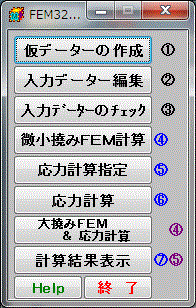　メニュー画面
　計算は、メニューに沿って順次実行します。

①仮データーの作成
　仮データーは、編集用元となる単純な形状を用意するもので、長方形ブロック、円柱、円筒が準備出来る様になっています。

②入力データーの編集
　仮データーで作成したもの、或いは、一度計算使用したもの等の入力データーの編集を行います。

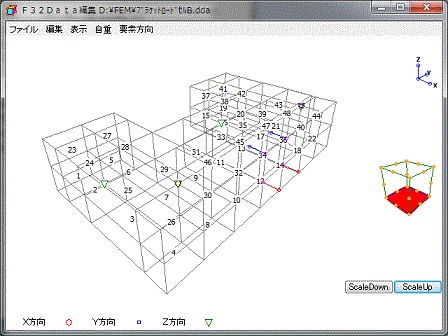
　要素の追加、削除、固定点、外力、変位、節点座標、ガウス積分点数、収束判定値、材質等の変更が可能になっています。
特に固定点については、正しく設定しないと、計算結果に大きな差が出るので注意が必要です。
③入力データーのチェック
　入力したデーターに問題が無いか確認する為のものです。
要素数が少ない場合は、特にチェックをしなくても良いでしょうが、要素数が多く計算に時間が掛かる場合は、先にチェックをした方が良いでしょう。
④微小撓みＦＥＭ計算
　たわみが小さい場合の計算です。
⑤応力計算指定
　
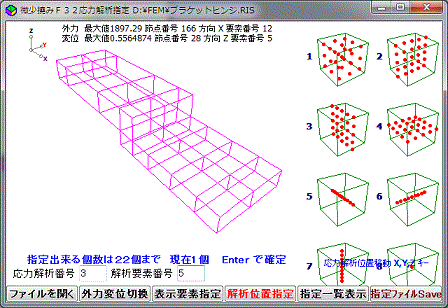
　応力を計算する要素と、計算点を指定します、計算点のパターンは、５，　３×３×３，　５×５　です。
応力計算の計算点の指定は、微小撓み計算の場合のみです。
⑥応力計算
　応力計算の指定に従って、微小撓みの応力の計算をします、計算指定用のファイルが保存されている必要があります。
⑦計算結果表示
　応力計算された結果の表示をします。

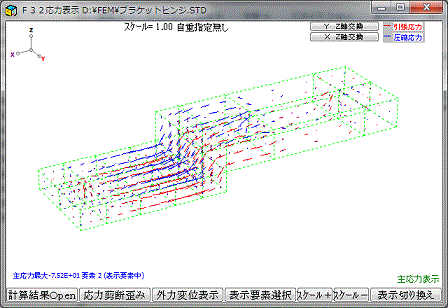
　主応力、引張圧縮、せん断、撓み、外力等を切替えて表示が可能です。
’④大撓み＆ＦＥＭ計算
　
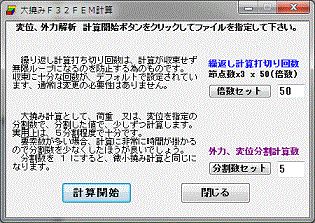
　大撓みの計算をします。
大撓みの場合、荷重の分割して、分割した回数分計算する為、剛性マトリックス、応力計算を続けて行うので、応力の計算は要素中央一ヶ所と　３×３×３　に限定して行います。
分割数は、５　程度良いのですが、撓みが非常に大きい場合は、分割数を増やします。
しかし、回転モーメントは与えることが出来ないので、分割数は２０程度以上にする必要はあまりないと思います。

次の違う計算方法で、同じデーターのものを計算した結果です。
幅　４㎜　　　板厚　0.2㎜　　　長さ　40㎜　　　荷重　0.2N　　材質SUS3301　ばね材

　ラーメンは簡単なＦＥＭ計算、板バネは薄板バネの計算からダウンロードしていただければ、計算が出来ます。
撓み量も、最大応力も殆ど同じ値になっていて、アイソパラメトリックソリッドモデルの計算が良い結果となっていることがわかります。
微小撓み計算の方が、撓みと応力が大きくなるのは、材料の変形による剛性の補正がされないからです、本来は微小撓みの計算を上にあるような撓み量の計算に使用すべきではないのですが、計算結果の比較として取り上げました。
板バネの計算は、撓みによる補正がされており、大撓みの計算になっています。
　データーの入力方法さえ良くなれば、十分実用になります、筆者も実際に仕事に使用しました。

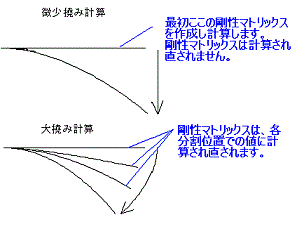
　微小撓み計算と、大撓み計算の差は、作図をしてみるとその差がよく解ります、微小撓み'(一回の計算）で、撓みが大きくなると、垂直荷重の場合、要素が伸びたように真っ直ぐ下へ変位し、現実にはあり得ない形状となりますが、大撓み計算（分割計算）では、実際の撓みとほぼ近似した撓みとなります。
どれぐらい撓むのかわからない場合は、最初から大撓み（分割計算）をした方が手間が省けて良いでしょう。

　Fem3200J.zip

各種プログラム計算例に戻る