exponential function 指数関数
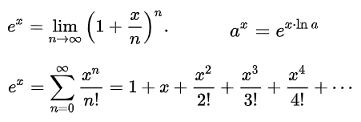 指数関数の詳細については、Wikipedia
指数関数 を参照して下さい。
指数関数の詳細については、Wikipedia
指数関数 を参照して下さい。
此処では、多倍長演算につい検討します。
double, extendedの精度の計算はDelphiに標準の関数として組み込まれています。
多倍長演算の組み込みについては、ベルヌーイ数 その4を参照して下さい。
自然指数関数の計算には、上図の級数展開式を使用しますが、x
の値が小さいときは、直ぐに収束しますが、大きくなると、計算に時間がかかります。
そこで、 ex = e(s+t)
= es ・ et
の様にして計算します。
et のtの値は
t = x-int(x/ln2)ln2 で求めます、es
の値は、k = int(x/ln2) es
= 2k として求めることが出来ます。
tの値は、ln2 (0.693147)~0 となり、級数計算を高速で行う事が出来ます。
xの値がマイナスの場合は、符号をとって正数とし
et を計算その後、逆数にします、es
は (1/2)k とします。
2或いは1/2のk乗の計算が有りますが、単純に計算すると時間が掛かるので、
k 任意の正の乗数 // z^k z = 2 or 1/2
w := 2 or w := 1/2 // w = z^1
ans := 1; // 初期値 = 1 *
z^0 1でなく任意の値でokです
while
k<> 0 do begin
if k and
1 = 1 then ans ::= ans * w; //
ans = ans,"* z^1", "* z^2","* z^4",
w ::= w
* w; // w = z^2, z^4, z^8, z^16
k ::= k shr
1; // 1bit 右シフト
end;
の様にすれば、大幅に乗算回数を減らすことができます、例えば、255乗の計算が16回の乗算で済みます。
指数関数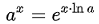 の計算には、自然対数の計算も必要となります。
の計算には、自然対数の計算も必要となります。
自然指数関数の計算が出来れば、容易に双曲線関数の計算が出来ます。
双曲線関数は、級数展開でも計算が出来ますが、sinh, cosh, tanh = sinh/cosh
以外の計算には、ベルヌーイ数、或いは、オイラー数が必要となります。
ベルヌーイ数やオイラー数を使用した級数展開の場合、ベルヌーイ数、オイラー数の値が大きくなり、演算に時間が掛かりあまり良い方法では無いようです。

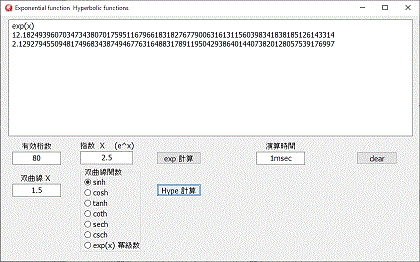 左図 "exp 計算ボタン"が
ex の高速計算で、ラジオボタン選択のexp(x)が級数展開のみによる計算ですので、演算時間の比較が出来ます。
左図 "exp 計算ボタン"が
ex の高速計算で、ラジオボタン選択のexp(x)が級数展開のみによる計算ですので、演算時間の比較が出来ます。
プログラム
Maim.pas
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls, system.Diagnostics;
type
TForm1 = class(TForm)
Memo1: TMemo;
X_Edit: TLabeledEdit;
PrecisionEdit: TLabeledEdit;
calc_Btn: TBitBtn;
clearBtn: TBitBtn;
Hype_Edit: TLabeledEdit;
RadioGroup1: TRadioGroup;
Hype_Btn: TBitBtn;
TimeEdit: TLabeledEdit;
procedure calc_BtnClick(Sender: TObject);
procedure clearBtnClick(Sender: TObject);
procedure Hype_BtnClick(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses exp_sub, Velthuis.Bigdecimals, Velthuis.bigintegers;
// 有効桁数入力
function InPrecision(s: string; m: integer): integer;
var
ch : integer;
begin
val(s, Result, ch);
if ch <> 0 then begin
application.MessageBox('有効桁数に間違いがあります。','注意',0);
result := -1;
exit;
end;
if Result < 1 then begin
application.MessageBox('有効桁数は1以上にしてください。','注意',0);
end;
if m = 0 then begin
if Result > 5000 then begin
application.MessageBox('有効桁数は5000迄にしてください。','注意',0);
result := -1;
end;
end
else
if Result > 50000 then begin
application.MessageBox('有効桁数は50000迄にしてください。','注意',0);
result := -1;
end;
end;
// 指数の無い場合の数値確認
// x: 'e','E'のない数字文字列
// ca: 0 '.' がある場合 1 ない場合
// 問題が無い場合 0を返します
function numeralfloatcheck(x: string; ca: byte): integer;
var
len, dn, n, d : integer;
num, numb : string;
flg : boolean;
snum : integer;
begin
len := length(x); // 文字長さ
snum := 1;
num := x[1]; // 1文字目
dn := 0;
flg := true;
if num = '+' then inc(snum); // '+' パス
if num = '-' then inc(snum); // '-' パス
if num = '.' then begin // '.'
inc(dn); // '.'カウントインクリメント
inc(snum); // パス
end;
for n := snum to len do begin // snum からlen 迄数値確認
num := x[n];
if num = '.' then begin // '.'
inc(dn); // '.'カウントインクリメント
continue; // パス
end;
flg := false;
for d := 0 to 9 do begin // 0~9の値か確認
numb := inttostr(d);
if numb = num then begin
flg := true;
break;
end;
end;
if flg = false then break;
end;
if ca = 0 then begin // '.'あり条件だったら
if dn > 1 then flg := false; // '.'1個迄なら0k
end
else // '.'無条件だったら
if dn > 0 then flg := false; // '.'があったらMG
if flg then result := 0
else result := 1;
end;
// 入力確認
function incheck(s, m: string): boolean;
const
ec = 'e';
eo = 'E';
dt = '.';
var
fs, es : string;
ch, p, po, leng : integer;
begin
result := false;
p := pos(ec, s); // 'e' の位置
po := pos(eo, s); // 'E' の位置
p := p + po;
if p = 0 then begin // 'e' 'E' が無かったら
ch := numeralfloatcheck(s, 0); // '.'がある条件で確認無くても良い
if ch <> 0 then begin
application.MessageBox(' 入力値に間違いがあります。','注意',0);
exit;
end;
result := true;
exit;
end;
leng := length(s);
fs := '';
fs := copy(s, 1, p - 1); // 'e'の前の文字取り出し
es := '';
es := copy(s, p + 1, leng - p); // 'e'の後ろの文字取り出し
ch := numeralfloatcheck(fs, 0); // 'e'の前の文字の確認 '.'がある条件で確認無くても良い
if ch <> 0 then begin
application.MessageBox(' 入力値に間違いがあります。','注意',0);
exit;
end;
if es <> '' then begin // 'e'の後ろの文字確認
ch := numeralfloatcheck(es, 1); // '.'が無い条件で確認
if ch <> 0 then begin
application.MessageBox(' 入力値に間違いがあります。','注意',0);
exit;
end;
end;
result := true;
end;
procedure TForm1.Hype_BtnClick(Sender: TObject);
var
Precision : integer;
x, ans : bigdecimal;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
k: integer;
begin
if not incheck(X_Edit.Text, '双曲線Xの') then exit;
Precision := InPrecision(PrecisionEdit.Text, 0); // 有効桁数入力
if Precision < 1 then exit;
BigDecimal.DefaultPrecision := Precision;
x := Hype_Edit.Text;
StopWatch := TStopwatch.StartNew;
k := radioGroup1.ItemIndex;
ans := hyperbolic(x, k);
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
Timeedit.text := intTostr(ElapsedMillseconds) + 'msec';
memo1.Lines.Append(ans.ToString);
end;
procedure TForm1.calc_BtnClick(Sender: TObject);
var
Precision : integer;
x, ans : bigdecimal;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
begin
if not incheck(X_Edit.Text, '指数Xの') then exit;
Precision := InPrecision(PrecisionEdit.Text, 0); // 有効桁数入力
if Precision < 1 then exit;
BigDecimal.DefaultPrecision := Precision;
x := X_Edit.Text;
StopWatch := TStopwatch.StartNew;
ans := exp_big(x);
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
Timeedit.text := intTostr(ElapsedMillseconds) + 'msec';
memo1.Lines.Append(ans.ToString);
end;
procedure TForm1.clearBtnClick(Sender: TObject);
begin
memo1.Clear;
end;
end.
exp_sub.pas
unit exp_sub;
interface
uses Velthuis.Bigdecimals, System.SysUtils, Vcl.Forms, Velthuis.BigIntegers, main;
function exp_big(x: bigdecimal): bigdecimal;
function sinh_big(x: bigdecimal): bigdecimal;
function cosh_big(x: bigdecimal): bigdecimal;
function tanh_big(x: bigdecimal): bigdecimal;
function coth_big(x: bigdecimal): bigdecimal;
function sech_big(x: bigdecimal): bigdecimal;
function csch_big(x: bigdecimal): bigdecimal;
function exp_test(x: bigdecimal): bigdecimal;
function hyperbolic(x: bigdecimal; k: integer): bigdecimal;
implementation
// 小さい値のlog計算
// x 実数
// dpcs 有効桁数
// ans log値
// 1e-4~1e4 が計算出来る限度
function Log_s_big(x: bigdecimal; dpcs: integer): bigdecimal;
var
one, two, x1, x2, i, s, last: bigdecimal;
begin
one := '1';
two := '2';
x1 := (x - one) / (x + one); // x1 = (x-1)/(x+1)
x2 := x1 * x1; // x1^2
x2 := x2.RoundToPrecision(dpcs);
i := one; // i=1
s := x1; // s初期値
repeat
x1 := x1 * x2; // x1^2n+1
x1 := x1.RoundToPrecision(dpcs);
i := i + two; // 2n+1
last := s; // 判定用sの値保存
s := s + x1 / i; // Σs = s + x1^2n+1 / (2n+1)
s := s.RoundToPrecision(dpcs); // 収束判定の為指定有効桁数以下丸め
until last = s; // 収束判定
result := two * s;
// Form1.Memo1.Lines.Append(intTostr(k));
end;
// exp(x) e^x 冪級数 テイラー級数
// exp(x) = 1 + x + x^2/2! + x^3/3! + x^4/4! ....
function exp_test(x: bigdecimal): bigdecimal;
var
dpcs : integer;
a, e, prev, zero, one, two, d : bigdecimal;
i, ione: bigInteger;
begin
dpcs := BigDecimal.DefaultPrecision;
zero := '0';
one := '1';
two := '2';
e := x; // exp(t)計算開始 e=x
if x < zero then e := -x; // x が負数だったらe 正数に
d := e; // d 初期値 e = /x/
a := d; // a 初期値 d = e = /x/
i := '2';
ione := '1';
repeat
prev := e; // 判定値保存
a := a * (d / i); // a = (d^i)/(i!)
a := a.RoundToPrecision(dpcs);
e := e + a; // e = e + (d^i)/(i!)
e := e.RoundToPrecision(dpcs);
i := i + ione; // inc(i)
until e = prev; // 桁落ちにより値が変わらなくなったら終了
e := e + one; // e = 1 + d + d^2/2! + d^3/3! ~
e := e.RoundToPrecision(dpcs);
one := one.RoundToPrecision(dpcs);
if x < 0 then e := one / e; // xが負数だったら答えは逆数
result := e;
end;
// sub exp(x) e^x
// exp(x)=exp(s+t)=exp(s)exp(t)
// k 2の指数 exp(s)=2^k
// x exp(t)の値
// exp(x)=exp(t) * 2^k
// dpcs 有効桁数
function expb(x: Bigdecimal; k: bigInteger; dpcs: integer): Bigdecimal;
var
w : bigdecimal;
izero, ione, ks : bigInteger;
begin
izero := '0';
ione := '1';
if k >= izero then w := '2' // k正数 2 べき乗初期値
else begin // k負数
w := '0.5'; // 1/2 べき乗初期値
k := -k; // k負数->正数
end;
while k <> izero do begin // kがゼロになるまで実行 exp(t)exp(s)
if k and ione = ione then begin // kの最下位ビットが1だったら
x := x * w; // exp(t) * 2^k'
x := x.RoundToPrecision(dpcs);
end;
w := w * w; // べき乗 w=2,4,16,256 2^1.2^2,2^4,2^8
// or w = 1/2,1/4,1/16,1/256 0.5^1,0.5^2,0.5^4,0.5^8
w := w.RoundToPrecision(dpcs);
bigInteger.ShiftRight(k, 1, ks); // kの値右シフト1ビット
k := ks;
end;
result := x; // exp(t) * 2^k
end;
// exp(x) e^x
// exp(x)=exp(s+t)=exp(s)exp(t)
// x eの指数
function expa(x: bigdecimal): bigdecimal;
var
neg : boolean;
dpcs : integer;
t, km, a, e, prev, LOG2, zero, one, two, d : bigdecimal;
k, i, ione: bigInteger;
begin
d := '100000000';
if x > d then begin
result := '0';
application.MessageBox('値が大きすぎます。','注意',0);
exit;
end;
dpcs := BigDecimal.DefaultPrecision;
zero := '0';
one := '1';
two := '2';
LOG2 := log_s_big(two, dpcs); // log(2)
km := x / LOG2; //
km := km.Floor; // 小数点以下切り捨て 2^km = exp(s)
t := x - km * LOG2; // t "exp(t)"
// form1.Memo1.Lines.Append(t.ToPlainString);
neg := false;
if t < zero then begin // t が負数なら
neg := true; // 負数フラグセット
t := -t; // 符号反転 負数->正数
end;
e := one + t; // exp(t)計算開始 テイラー級数 e初期値
a := t; // a初期値
i := '2';
ione := '1';
repeat
prev := e;
a := a * (t / i); // a = (t^i)/(i!)
a := a.RoundToPrecision(dpcs);
e := e + a; // Σ
e := e.RoundToPrecision(dpcs);
i := i + ione; // inc(i)
until e = prev; // 収束判定
if neg then e := one / e; // 負数なら逆数
k := km.AsBigInteger; // float -> int
// e = exp(t)
result := expb(e, k, dpcs); // exp(x) = exp(t) * 2^k = exp(t) * exp(s)
end;
// e^x exp(x)
function exp_big(x: bigDecimal): bigdecimal;
var
pcsBack, dpcs : integer;
rmback : BigDecimal.RoundingMode;
begin
pcsBack := BigDecimal.DefaultPrecision; // 有効桁数バックアップ
rmBack := BigDecimal.DefaultRoundingMode; // 丸めモードバックアップ
dpcs := pcsBack + 5; // 指定有効桁数 + α
BigDecimal.DefaultPrecision := dpcs;
BigDecimal.DefaultRoundingMode := rmNearesteven;
x := x.RoundToPrecision(dpcs);
result := expa(x);
result := result.RoundToPrecision(pcsBack); // 指定有効桁数に丸め
BigDecimal.DefaultPrecision := pcsBack; // 有効桁数復帰
BigDecimal.DefaultRoundingMode := rmBack; // 丸めモード復帰
end;
// sinh(x) = (e^x - e^-x) / 2
function sinh_big(x : bigdecimal): bigdecimal;
var
dpcs : integer;
two, a, b, c : bigdecimal;
begin
dpcs := BigDecimal.DefaultPrecision; // 有効桁数
two := '2';
x := x.RoundToPrecision(dpcs);
a := expa(x);
b := expa(-x);
c := a - b;
c := c.RoundToPrecision(dpcs);
result := c / two;
end;
// cosh(x) = (e^x + e^-x) / 2
function cosh_big(x : bigdecimal): bigdecimal;
var
dpcs : integer;
two, a, b, c : bigdecimal;
begin
dpcs := BigDecimal.DefaultPrecision; // 有効桁数
two := '2';
x := x.RoundToPrecision(dpcs);
a := expa(x);
b := expa(-x);
c := a + b;
c := c.RoundToPrecision(dpcs);
result := c / two;
end;
// tanh(x) = (e^x - e^-x) / (e^x + e^-x)
function tanh_big(x : bigdecimal): bigdecimal;
var
dpcs : integer;
a, b, c, d : bigdecimal;
begin
dpcs := BigDecimal.DefaultPrecision; // 有効桁数
x := x.RoundToPrecision(dpcs);
a := expa(x);
b := expa(-x);
c := a - b;
c := c.RoundToPrecision(dpcs);
d := a + b;
d := d.RoundToPrecision(dpcs);
result := c / d;
end;
// coth(x) = (e^x + e^-x) / (e^x - e^-x)
// x ≠ 0
function coth_big(x : bigdecimal): bigdecimal;
var
dpcs : integer;
zero, a, b, c, d : bigdecimal;
begin
dpcs := BigDecimal.DefaultPrecision; // 有効桁数
x := x.RoundToPrecision(dpcs);
a := expa(x);
b := expa(-x);
c := a + b;
c := c.RoundToPrecision(dpcs);
d := a - b;
d := d.RoundToPrecision(dpcs);
result := c / d;
end;
// sech(x) = 2 / (e^x + e^-x)
function sech_big(x : bigdecimal): bigdecimal;
var
dpcs : integer;
two, a, b, c : bigdecimal;
begin
dpcs := BigDecimal.DefaultPrecision; // 有効桁数
two := '2';
x := x.RoundToPrecision(dpcs);
a := expa(x);
b := expa(-x);
c := a + b;
c := c.RoundToPrecision(dpcs);
result := two / c;
end;
// csch(x) = 2 / (e^x - e^-x)
// x ≠ 0
function csch_big(x : bigdecimal): bigdecimal;
var
dpcs : integer;
two, a, b, c : bigdecimal;
begin
dpcs := BigDecimal.DefaultPrecision; // 有効桁数
two := '2';
x := x.RoundToPrecision(dpcs);
a := expa(x);
b := expa(-x);
c := a - b;
c := c.RoundToPrecision(dpcs);
result := two / c;
end;
// x : 双曲線引数
// k : 双曲線種類
function hyperbolic(x: bigdecimal; k: integer): bigdecimal;
var
pcsBack, dpcs : integer;
rmback : BigDecimal.RoundingMode;
zero: bigdecimal;
begin
zero := '0';
if k = 3 or 5 then begin
if x = zero then begin
application.MessageBox('csch(x)の引数値xがゼロです。','注意',0);
result := '0';
exit;
end;
end;
pcsBack := BigDecimal.DefaultPrecision; // 有効桁数バックアップ
rmBack := BigDecimal.DefaultRoundingMode; // 丸めモードバックアップ
dpcs := pcsBack + 5; // 指定有効桁数 + α
BigDecimal.DefaultPrecision := dpcs;
BigDecimal.DefaultRoundingMode := rmNearesteven;
case k of
0 : result := sinh_big(x);
1 : result := cosh_big(x);
2 : result := tanh_big(x);
3 : result := coth_big(x);
4 : result := sech_big(x);
5 : result := csch_big(x);
6 : result := exp_test(x);
end;
result := result.RoundToPrecision(pcsBack); // 指定有効桁数に丸め
BigDecimal.DefaultPrecision := pcsBack; // 有効桁数復帰
BigDecimal.DefaultRoundingMode := rmBack; // 丸めモード復帰
end;
end.
 exponential_function.zip
exponential_function.zip
三角関数、逆三角関数、その他関数 に戻る
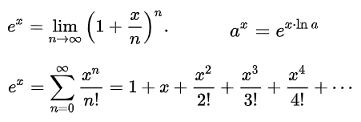 指数関数の詳細については、Wikipedia
指数関数 を参照して下さい。
指数関数の詳細については、Wikipedia
指数関数 を参照して下さい。
 左図 "exp 計算ボタン"が
ex の高速計算で、ラジオボタン選択のexp(x)が級数展開のみによる計算ですので、演算時間の比較が出来ます。
左図 "exp 計算ボタン"が
ex の高速計算で、ラジオボタン選択のexp(x)が級数展開のみによる計算ですので、演算時間の比較が出来ます。