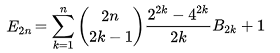
オイラー数 その3
オイラー数の計算に、ベルヌーイ数から変換する数式が有ったので、試してみました。
ベルヌーイ数を利用して、オイラー数が計算できる参考のプログラムです。
当然オイラー数を利用して、ベルヌーイ数を求める計算式もありますが、参考程度なので此処では取り上げないことにしました。
詳細はウィキペディアを参照してください。
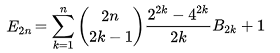
計算式は上記です。
二項係数を使用して、オイラー数を計算する他のプログラムと同じように見えますが、E10を計算したとすると、K=1～10迄のΣ値を計算するだけなので、意外と速く計算できます。
他の二項係数による計算では、E0を計算Σk=0でE1をΣk=0～2でE2を計算してからΣk=0～4でE4を計算するように、指定されたEnの値を求めるのに、E1,E2～Enと繰り返しΣ値を計算する必要があり非常に計算数が多くなり計算に時間が掛かりました。
ベルヌーイ数の計算は、二項係数を使用しない計算で先に計算をしておきます。
プログラム
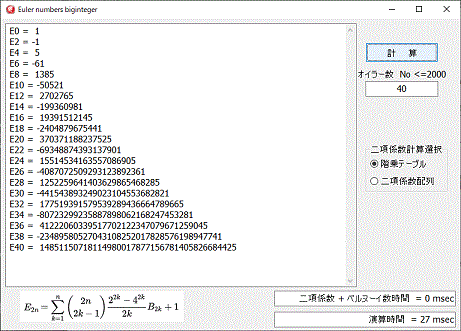E2000で0.8秒(cpu依存)程度で計算出来ます。
プログラムには、Bigintegerを使用します。
bigintegerの組み込みについては、ベルヌーイ数 その４を参照してください。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, system.Diagnostics, Vcl.Buttons,
Vcl.ExtCtrls, Vcl.Imaging.pngimage;
type
TForm1 = class(TForm)
Memo1: TMemo;
BitBtn1: TBitBtn;
LabeledEdit1: TLabeledEdit;
Image1: TImage;
Edit1: TEdit;
RadioGroup1: TRadioGroup;
Edit2: TEdit;
procedure BitBtn1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
uses Velthuis.BigIntegers;
{$R *.dfm}
var
fact : array of biginteger; // 階乗テーブル配列
com : array of array of Biginteger; // nCk ck配列
mback : integer = -1;
rindex : integer = -1;
// nCk C[n, k] 二項係数配列の作成 Biginteger
// 二項係数の対称性を利用しkの配列のサイズはnの二分の一
procedure calac_com(size: integer);
var
i, j: integer;
begin
setlength(com, size + 1, size div 2 + 1);
com[0, 0] := 1;
for i := 1 to size do begin
com[i, 0] := 1;
for j := 1 to size div 2 do
com[i, j] := (com[i - 1, j - 1] + com[i - 1, j]);
end;
end;
// 階乗テーブル作成
// 0～n
procedure factorialtable(n: integer);
var
j : integer;
begin
setlength(fact, n + 1); // 階乗テーブル配列確保
fact[0] := 1; // 0!
if n = 0 then exit;
fact[1] := 1; // 1!
if n = 1 then exit;
for j := 2 to n do
fact[j] := fact[j - 1] * j; // 2～n!
end;
// 二項係数 biginteger
function binomialBig(n, k: int64): biginteger;
begin
result := fact[n] div (fact[k] * fact[n - k]);
end;
// 最大公約数 ユークリッドの互除法 biginteger
function gcd(x, y: biginteger): biginteger;
var
t : biginteger;
begin
while y <> 0 do begin
t := x mod y;
x := y;
y := t;
end;
result := x;
end;
// ベルヌーイ数テーブルの作成 biginteger
// N 最大ベルヌーイNo
// Bn,Bd ベルヌーイ数配列 分子,分母 No0と偶数Noのみ配列に保存
// B1= ±1/2, Bn=0の n奇数の値はテーブルに無し
// n = 2000 作成時約810msec(cpu依存)
procedure Bernoulli(N: integer; var Bn, Bd: array of biginteger);
var
i, m, md2 : integer;
q : biginteger; // 分母の値計算用
b1, b2 : biginteger; // 分子,分母
d : biginteger; // 最大公約数
t : array of biginteger; // t[]は分子の値計算用
begin
// B0 = 1
bn[0] := 1; // bn[0] B0 分子
bd[0] := 1; // bd[0] B0 分母
if N = 0 then exit;
// B2～Bn
setlength(t, N + 1); // 分子計算用配列確保 配列全て0(ゼロ)
q := 1; // 分母計算初期値
t[1] := 1; // 分子計算初期値
for m := 2 to N do begin
for i := 1 to m - 1 do t[i - 1] := i * t[i]; // 分子計算
t[m - 1] := 0; // 〃
for i := m downto 2 do t[i] := t[i] + t[i - 2]; // 〃
if m mod 2 = 0 then begin // 偶数ベルヌーイNoなら
q := q * 4; // 分母計算
b1 := m * t[0]; // 分子
b2 := q * (q - 1); // 分母
d := gcd(b1, b2); // 最大公約数
b1 := b1 div d; // 分子
b2 := b2 div d; // 分母
if m mod 4 = 0 then b1 := -b1; // 4の倍数のベルヌーイNoは負数
md2 := m div 2; // 配列No
bn[md2] := b1; // bn[1] ～ bn[n/2]配列に保存 奇数No無し 分子
bd[md2] := b2; // bd[1] ～ bd[n/2] 〃 分母
end;
end;
end;
// オイラー数計算 Biginteger
// m: オイラー数 No
// m = 2000 変換時間 980msec(cpu 依存)
procedure TForm1.BitBtn1Click(Sender: TObject);
const
NM = 40; // 表示数切替 NM迄は一括表示
var // NMを超えたら指定数のみ表示
Bn, Bd : array of biginteger; // ベリヌーイ数配列 分子,分母
En, Ed : biginteger; // オイラー数 分子 分母
Tn, Td, g : biginteger; // 分子,分母,最大公約数
two, four : biginteger; // 2, 4
binomial : biginteger; // 二項係数
n, i, m : integer;
mstr : string;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
// ベルヌーイ数->オイラー数変換
// ベルヌーイ数配列はNo0と偶数No値のみ
// 変換後オイラー数は En
procedure calcEuler(n: integer);
var
k, j: integer;
begin
j := 0;
En := bn[j]; // 分子 1 (Σ=1)
Ed := bd[j]; // 分母 1
for j := 1 to n div 2 do begin // for k = 2 to n step 2
k := 2 * j; // 偶数項のみ計算
case RadioGroup1.ItemIndex of
0 : binomial := binomialBig(n, k - 1);
1 : begin
if (k - 1) <= n div 2 then binomial := com[n, k - 1]
else binomial := com[n, n - k + 1];
end;
end;
Tn := binomial * (biginteger.Pow(two, k) - biginteger.Pow(four, k)) * Bn[j];
Td := Bd[j] * k;
// Σ= 分数加算 En/Ed := En/Ed + Tn/Td
En := En * Td + Tn * Ed; // 分子計算
Ed := Ed * Td; // 分母計算
g := gcd(En, Ed); // 最大公約数
En := En div g;
Ed := Ed div g;
end;
end;
begin
val(labelededit1.Text, m, n);
if n <> 0 then begin
memo1.Text := 'オイラー数 Noに間違いがあります。';
exit;
end;
if m > 2000 then begin
memo1.Text := 'オイラー数 Noは2000迄にして下さい。';
exit;
end;
if m < 0 then begin
memo1.Text := 'オイラー数 Noは0以上にして下さい。';
exit;
end;
StopWatch := TStopwatch.StartNew;
setlength(Bn, m div 2 + 1); // ベルヌーイ数配列確保 分子
setlength(Bd, m div 2 + 1); // 〃 分母
Bernoulli(m, Bn, Bd); // ベルヌーイ数 配列データー作成
if (mback <> m) or (rindex <> RadioGroup1.ItemIndex) then
case RadioGroup1.ItemIndex of
0: factorialtable(m); // 階乗テーブル作成
1: calac_com(m);
end;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
if (mback <> m) or (rindex <> RadioGroup1.ItemIndex) then
Edit1.text := '二項係数 + ベルヌーイ数時間 = ' + intTostr(ElapsedMillseconds) + ' msec'
else
Edit1.text := 'ベルヌーイ数演算時間 = ' + intTostr(ElapsedMillseconds) + ' msec';
mback := m;
rindex := RadioGroup1.ItemIndex;
memo1.Clear;
two := 2;
four := 4;
// E0～ // m = 2000 変換時間 150msec(cpu依存)
if m <= NM then // No が NM 以下なら m迄 計算
for i := 0 to m div 2 do begin // for n = 0 to m step 2
n := i * 2; // 偶数No
calcEuler(n); // ベルヌーイ数->オイラー数変換
if En < 0 then mstr := ' = ' else mstr := ' = ';
memo1.lines.append('E' + inttostr(n) + mstr + En.ToString);
end;
// 奇数 No指定の時 0表示
if (m mod 2 <> 0) then begin
En := 0;
memo1.lines.append('E' + inttostr(m) + ' = ' + En.ToString);
end
else
// 偶数 No で NMより大きいとき表示
if m > NM then begin
calcEuler(m); // ベルヌーイ数->オイラー数変換
if En < 0 then mstr := ' = ' else mstr := ' = ';
memo1.lines.append('E' + inttostr(m) + mstr + En.ToString);
end;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
Edit2.text := '演算時間 = ' + intTostr(ElapsedMillseconds) + ' msec';
end;
end.
Euler_number_3.zip
各種プログラム計算例に戻る