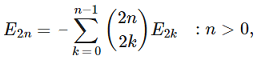の計算が一番高速に計算出来たので、更に高速に計算する方法を検討します。計算の時間に大きな影響を及ぼしているのは、二項係数の計算なので、この計算の高速化です。
2022-01-09
二項係数計算3の配列サイズ変更 メモリーの使用量縮小
2022-01-04
説明の追加
2021-12-31
二項係数用配列の確保の方法変更。
オイラー数 その２
オイラー数その１で、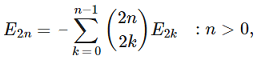の計算が一番高速に計算出来たので、更に高速に計算する方法を検討します。
計算の時間に大きな影響を及ぼしているのは、二項係数の計算なので、この計算の高速化です。
高速 二項計算の方法について探すと、フェルマーの小定理を利用した方法があり、時間の掛かる割り算を逆数を掛ける掛け算にして高速に計算するという方法が見つかったので、最初に検討してみる事にしました。
理論的な事は、"高速 二項係数" でインターネットで探して見てください。
計算用の配列の作成、階乗の配列を作成するよりは可成り計算量が多くなっていますが、最初に作成してしまえば問題ありませんので、この方法で計算していました。
しかし、オイラー数の計算時間に比べて、二項係数計算用の配列の作成時間が短いので、オイラー数の大きさに合わせて配列の大きさを変更し、二項係数用配列の作成と、オイラー数計算をその都度行う様にしました。
変更した最大の理由は、二項係数計算で、逆数を利用した計算の時、オイラー数Noが小さいときの計算の速度を上げる為です。
配列の大きさを小さくすると、素数として使用する値を小さく出来、計算を高速化出来るからです。
二項係数計算 1
この計算では、modp(mod64)は、必ずしも素数である必要性はありませんが正しく計算出来る値は探し出す必要があります。
const mod64 = 1000000007; // 素数あるいは、素数代替数 var fact64: array of int64; inv64: array of int64; fact64_inv: array of int64; // 配列の作成 int64 procedure init64_nck(size: integer); var i: integer; begin setlength(fact64, size + 1); setlength(fact64_inv, size + 1); setlength(inv64, size + 1); fact64[0] := 1; fact64[1] := 1; fact64_inv[0] := 1; fact64_inv[1] := 1; inv64[0] := 1; inv64[1] := 1; for i := 2 to size do begin fact64[i] := fact64[i - 1] * i mod mod64; // 階乗 inv64[i] := mod64 - inv64[mod64 mod i] * (mod64 div i) mod mod64; // 逆数 fact64_inv[i] := fact64_inv[i - 1] * inv64[i] mod mod64; // 逆数の階乗 end; end;
二項係数計算 2 フェルマーの小定理
modp(mod64)の値は素数でないと成り立ちません。
const mod64 = 1000000007; // 素数 var fact64: array of int64; fact64_inv: array of int64; function invcalc(x : int64): int64; // 逆数計算 var res, k, y : int64; begin res := 1; k := mod64 - 2; y := x; while K <> 0 do begin if k and 1 = 1 then res := (res * y) mod mod64; y := (y * y) mod mod64; k := k div 2; end; result := res; end; procedure init(size: integer); var i : integer; begin setlength(fact64, size + 1); setlength(fact64_inv, size + 1); fact64[0] := 1; for i := 1 to size do fact64[i] := (fact64[i - 1] * i) mod mod64; // 階乗 fact64_inv[size] := invcalc(fact64[size]); // 逆数 for i := size - 1 downto 0 do fact64_inv[i] := (fact64_inv[i + 1] * (i + 1)) mod mod64; end;
一度、配列の作成をしてしまえば、Function で二項係数の値を求める事ができます。
// 二項係数
function binomialint64(n, k: integer): int64;
begin
result := fact64[n] * (fact64_inv[k] * fact64_inv[n - k] mod mod64) mod mod64;
end;
確かに、割り算は無くなっていますが、mod剰余の計算が二回になっています。
modの計算を一回にすることも出来ますが、掛け算が三個繋がるので、オーバーフローが発生しやすくなります。
上の計算式は、int64(long long)ですが、実際に計算に時間が掛かるのは、EnのNoが大きい時でBigintegerの計算なので、二項係数の計算もBigintegerとなります。
プログラムは、最初にint64で作成して、問題が無かったらBigintegerに変換しています。
問題は、素数の設定です。
高速二項係数のプログラムを検索すると、long long(64ビット)の計算で素数1000000007を使用した例で、n
,kの値(配列の数)5000位迄設定できるように書かれているものがありましたが、long
long(64ビット)では、n=32,k=16が限度で、これ以上ではオーバーフローしますが、整数演算なのでオーバーフローは検出されません。
上記のプログラムでは、size=32が限度となりますが、これは二項係数の値で、オイラー数を計算すると、n=22を超えた場合オイラー数がint64(long
long)を超えオーバーフローします。
n=22だと、素数の値は、800011で良いことになります。
更に、計算をしてみると、二項係数計算1では、素数ではない800027でも正しい二項係数の値となりました、必ずしも素数を必要とするわけでは無いようです。
二項係数計算2の場合は、素数でないと正しい値を得ることは出来ません。
次は、bigintegerで、n=2000での値の設定です。
まずは、階乗での二項係数の計算から、n = 2000 k= 1000
の二項係数nCkの最大値を求めます、nに対してn/2のkの値が最大値となります。
最大値は、2.0482E600 の値となりました。
これより大きい値の素数の設定が必要となりますが、ここ迄大きいと、素数検索や、素数生成のプログラムでは、どれぐらいの時間を要するかわからない位時間がかかります、実際にプログラムを作ってみました。
2.0482E600より大きな値の仮の素数値を設定して計算し、階乗で:計算した、n=2000のオイラー数の結果と同じ結果が出れば、その値は、素数とは違うかもしれませんが問題の無い値となります。
2.0482E600 より大きい値として、1E601=10^601 を設定 更に奇数を加算 +
3 ,7,11,13,17,19,23,29,31 >>で、19で正しい答えがでました。
意外と早く見つける事が出来て正しい答えが得られたので、10^601 + 19 は素数とは違うかもしれませんが二項係数を計算するのには問題の無い値です。
実際に計算をしてみると、n=1750 位迄は階乗の配列を使用した方が速く、これを超えると、逆数を利用した計算が速くなります。
n=2000 で、階乗の配列使用で、22sec (cpu依存)に対して、逆数使用で 16sec(cpu依存) となりました。
あまり、改善されません。
階乗の配列を使用した場合に比べて、オイラー数Noの小さい時に計算に時間が掛かるので、オイラー数Noに合わせて、配列のサイズも変更するようにした結果、inv逆数を使用した場合と、階乗の配列を使用した場合で大差ない時間で計算が出来るようになりました。
しかし、ベルヌーイ数の計算に比べて、根本的に遅いので、メモリーを大量に使用しますが、二項係数の配列を先に計算しておいて、オイラー数計算の時に、二項係数の計算の必要の無い方法を検討します。
二項係数計算 3
二項係数テーブル作成プログラム
var
comint: array of array of int64; // nCk ck配列 int64
procedure calac_comint(size: integer);
var
i, j: integer;
begin
setlength(comint, size + 1, size + 1);
comint[0, 0] := 1;
for i := 1 to size do begin
comint[i, 0] := 1;
for j := 1 to size do
comint[i, j] := comint[i - 1, j - 1] + comint[i - 1, j];
end;
end;
配列の大きさは、オイラー数No が2000だと、2001×2001となり可成り大きくなりますが、Bigintegerでも現在のパソコンなら問題のない大きさです。
テーブルの作成にはBiginteger時 0.3sec程必要としますが、初期化時だけなので問題のない時間です。
(二項係数配列作成のプログラムの計算には加算しかないので、意外と早く作成することができます。)
二項係数nCkの時の値は単に配列
comint[n][k] でオイラー数計算の時、演算の必要性が無いので、非常に高速に計算することが出来ます。
プログラムを作成して実行した結果 1.2sec(cpu依存)で、10倍以上速くなりました、配列作成の時間を入れても1.5secです。
配列の大きさの縮小
配列の中の二項係数の値は下記のようになります。
n k 0 1 2 3 4 5 6 0 1 0 0 0 0 0 0 1 1 1 0 0 0 0 0 2 1 2 1 0 0 0 0 3 1 3 3 1 0 0 0 4 1 4 6 4 0 0 0 5 1 5 10 10 5 0 0 6 1 6 15 20 15 6 1
配列のnの一番大きい場所を見ると、中心の値に対して左右対称になっています。(パスカルの三角形で表示すると、全て左右対象です。)
そこで、右側の赤文字の部分を省略すれば、配列の大きさと、配列を作成する時間を節約できます。
var
comint: array of array of int64; // nCk ck配列 int64
procedure calac_comint(size: integer);
var
i, j: integer;
begin
setlength(comint, size + 1, size div 2 + 1);
comint[0, 0] := 1;
for i := 1 to size do begin
comint[i, 0] := 1;
for j := 1 to i div 2 do
comint[i, j] := comint[i - 1, j - 1] + comint[i - 1, j];
end;
end;
comint[n, k] k <= n / 2
comint[n, n - k]] K > n / 2
配列の値を取り出すときに、kの値の判別を必要としますが、配列作成の時間が短くなり、トータルとしては変わりません。
プログラム
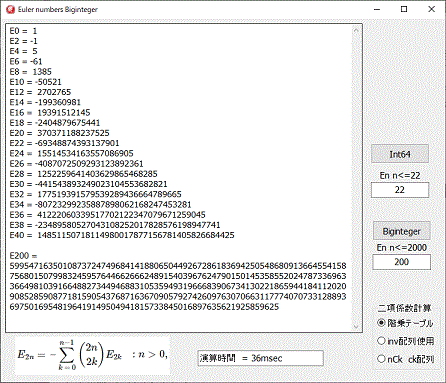二項係数の計算方法は、三種類設定が出来ます。
nCkの配列以外は、nを大きくすると、待ち時間が長くなります。
int64の計算の場合、n=22迄しか計算できないので、演算時間に殆ど差は出ません。
bigintegerの組み込みはベルヌーイ数 その４を参照してください。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, system.Diagnostics,
Vcl.ExtCtrls, Vcl.Imaging.pngimage;
type
TForm1 = class(TForm)
Memo1: TMemo;
Image1: TImage;
LabeledEdit1: TLabeledEdit;
BigIntegerBtn: TBitBtn;
LabeledEdit2: TLabeledEdit;
Int64Btn: TBitBtn;
RadioGroup1: TRadioGroup;
Edit1: TEdit;
procedure FormCreate(Sender: TObject);
procedure BigIntegerBtnClick(Sender: TObject);
procedure Int64BtnClick(Sender: TObject);
private
{ Private 宣言 }
function Ninput(var n: integer): boolean;
function NinputBig(var n: integer): boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses Velthuis.BigIntegers, system.Math;
const
NI = 22; // 最大オイラー 1nt64
NB = 2000; // 最大オイラー Biginteger
var
// int64用
mod64 : int64; // 素数用
fact64: array of Int64;
fact64_inv: array of Int64;
factdbl: array of double; // 階乗テーブル n=22の桁落ち防止の為 double設定
comint: array of array of int64; // nCk ck配列 int64
// biginteger用
modbig: Biginteger; // mod正解用
fact: array of BigInteger;
fact_inv: array of BigInteger;
factbig: array of BigInteger; // 階乗テーブル配列
com: array of array of Biginteger; // nCk ck配列
//--------------------------------- int64 --------------------------------------
// 階乗テーブル作成
procedure facttablemake(size: integer);
var
i: integer;
begin
setlength(factdbl, size + 1);
factdbl[0] := 1;
factdbl[1] := 1;
for i := 2 to size do factdbl[i] := factdbl[i - 1] * i;
end;
// inv配列の作成 int64
procedure init64_nck(size: integer);
var
i: integer;
inv64: array of Int64;
begin
setlength(fact64, size + 1);
setlength(fact64_inv, size + 1);
setlength(inv64, size + 1);
// mod64 := 1000000007; // 1nt64 で 1000000007 は不向き
// 素数選択
// オイラー数計算ではint64は、size = 22 を超えるとオーバーフローします。
// if size <= 32 then mod64 := 601080397; // int64 素数 > 601080390 最大二項係数 n=32 k=16
if size <= 22 then mod64 := 705437; // int64 素数 > 705432 最大二項係数 n = 22 k=11
if size <= 16 then mod64 := 12889; // int64 素数 > 12870 最大二項係数 n = 16 k=8
fact64[0] := 1;
fact64[1] := 1;
fact64_inv[0] := 1;
fact64_inv[1] := 1;
inv64[0] := 0;
inv64[1] := 1;
for i := 2 to size do begin
fact64[i] := fact64[i - 1] * i mod mod64;
inv64[i] := mod64 - inv64[mod64 mod i] * (mod64 div i) mod mod64;
fact64_inv[i] := fact64_inv[i - 1] * inv64[i] mod mod64;
end;
end;
// nCk C[n, k] 二項係数配列の作成 int64
procedure calac_comint(size: integer);
var
i, j: integer;
begin
setlength(comint, size + 1, size div 2 + 1);
comint[0, 0] := 1;
for i := 1 to size do begin
comint[i, 0] := 1;
for j := 1 to size div 2 do
comint[i, j] := comint[i - 1, j - 1] + comint[i - 1, j];
end;
end;
// 二項係数 doubleの階乗配列使用
function binomialint(n, k: integer): int64;
begin
result := round(factdbl[n] / (factdbl[k] * factdbl[n - k]));
end;
// 二項係数 int64 div 無し inv使用
function binomialint64(n, k: integer): int64;
begin
result := fact64[n] * (fact64_inv[k] * fact64_inv[n - k] mod mod64) mod mod64;
end;
// オイラーNo入力処理
function TForm1.Ninput(var n: integer): boolean;
var
c : integer;
begin
result := true;
val(labelededit1.Text, n, c);
if c <> 0 then begin
memo1.Text := 'オイラーNo に間違いがあります。';
result := false;
exit;
end;
if n < 0 then begin
memo1.Text := 'オイラーNoはゼロ以上にして下さい。';
result := false;
end;
if n > NI then begin
memo1.Text := 'オイラーNo が大きすぎます' + intTostr(NI) + '迄です。';
result := false;
end;
end;
// オイラー数 Int64
procedure TForm1.Int64BtnClick(Sender: TObject);
label
N0;
var
n, n2, nd2 : integer;
En : array of Int64;
i, k, k2 : integer;
s : Int64;
mstr : string;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
begin
if not Ninput(n) then exit; // n数入力
Int64Btn.Enabled := false;
BigIntegerBtn.Enabled := false;
StopWatch := TStopwatch.StartNew;
memo1.Clear;
if n > 0 then
case RadioGroup1.ItemIndex of
0: facttablemake(n); // !テーブル
1: init64_nck(n); // inv配列
2: calac_comint(n); // nCk nk配列
end;
nd2 := n div 2;
setlength(En, nd2 + 1); // No=0 + 偶数No用配列確保
i := 0; // Kn [0] [1] [2] [3] [4] [5] [6]・・
En[i] := 1; // En 0 2 4 6 8 10 12・・
memo1.Lines.Append('E' + intTostr(i) + ' = ' + inttostr(En[i]));
if n = 0 then goto N0;
for i := 1 to nd2 do begin // for i = 2 to n step 2
s := 0;
n2 := i shl 1; // n2 = i * 2
for k := 0 to i - 1 do begin // ΣEk
k2 := k shl 1; // k2 = 2 * k
case RadioGroup1.ItemIndex of
0: s := s + binomialint(n2, k2) * En[k]; // !テーブル
1: s := s + binomialint64(n2, k2) * En[k]; // inv配列
2: begin // 二項係数の対称性利用
if k2 <= i then // k <= n / 2
s := s + comint[n2, k2] * En[k] // nCk nk配列
else
s := s + comint[n2, n2 - k2] * En[k]; // nCk nk配列
end;
end;
end;
En[i] := -s; // En[No/2] = -s
if s > 0 then mstr := ' = '
else mstr := ' = ';
memo1.Lines.Append('E' + intTostr(n2) + mstr + intTostr(En[i]));
end;
N0:
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
Edit1.text := '演算時間 = ' + intTostr(ElapsedMillseconds) + 'msec';
Int64Btn.Enabled := True;;
BigIntegerBtn.Enabled := true;
end;
//--------------------------- biginteger ---------------------------------------
// 階乗テーブル作成 Biginteger
procedure factmbigake(size: integer);
var
i : integer;
begin
// 階乗テーブル
setlength(factbig, size + 1);
factbig[0] := 1;
factbig[1] := 1;
for i := 2 to size do factbig[i] := factbig[i - 1] * i;
end;
// inv配列の作成 Biginteger
procedure init_nck(size: integer);
var
i : integer;
j : int64;
b : biginteger;
Ten : biginteger;
inv: array of BigInteger;
begin
Ten := biginteger.Ten;
// mod変換の値の選択 配列の大きさで値の選択 二項係数より大きくてより近い値の選択
// 素数でない値でも二項係数は正しく計算されますがが一応素数を用意しました。
if (size <= 2000) and (size > 1800) then begin modbig := 2049 * biginteger.Pow(Ten, 597) + 1759; size := 2000 end;
if (size <= 1800) and (size > 1600) then begin modbig := 1344 * biginteger.Pow(Ten, 537) + 2701; size := 1800 end;
if (size <= 1600) and (size > 1400) then begin modbig := 8868 * biginteger.Pow(Ten, 476) + 2021; size := 1600 end;
if (size <= 1400) and (size > 1200) then begin modbig := 5900 * biginteger.Pow(Ten, 416) + 321; size := 1400 end;
if (size <= 1200) and (size > 1000) then begin modbig := 3966 * biginteger.Pow(Ten, 356) + 611; size := 1200 end;
if (size <= 1000) and (size > 800) then begin modbig := 2703 * biginteger.Pow(Ten, 296) + 517; size := 1000 end;
if (size <= 800) and (size > 600) then begin modbig := 1881 * biginteger.Pow(Ten, 236) + 479; size := 800 end;
if (size <= 600) and (size > 400) then begin modbig := 1352 * biginteger.Pow(Ten, 176) + 653; size := 600 end;
if (size <= 400) and (size > 200) then begin modbig := 1030 * biginteger.Pow(Ten, 116) + 171; size := 400 end;
if size <= 200 then begin modbig := 9055 * biginteger.Pow(Ten, 55) + 33; size := 200 end;
setlength(fact, size + 1);
setlength(fact_inv, size + 1);
setlength(inv, size + 1);
fact[0] := 1;
fact[1] := 1;
fact_inv[0] := 1;
fact_inv[1] := 1;
inv[0] := 1;
inv[1] := 1;
for i := 2 to size do begin
fact[i] := fact[i - 1] * i mod modbig;
b := modbig mod i; // b < i
j := b.AsInt64; // biginteger -> 1nt64
inv[i] := modbig - inv[j] * (modbig div i) mod modbig;
fact_inv[i] := fact_inv[i - 1] * inv[i] mod modbig;
end;
end;
// nCk C[n, k] 二項係数配列の作成 Biginteger
// 二項係数の対称性を利用しkの配列のサイズはnの二分の一
procedure calac_com(size: integer);
var
i, j: integer;
begin
setlength(com, size + 1, size div 2 + 1);
com[0, 0] := 1;
for i := 1 to size do begin
com[i, 0] := 1;
for j := 1 to size div 2 do
com[i, j] := (com[i - 1, j - 1] + com[i - 1, j]);
end;
end;
// 二項係数 BigInteger 階乗配列使用
function binomialBigB(n, k: integer): BigInteger;
begin
result := factbig[n] div (factbig[k] * factbig[n - k]);
end;
// 二項係数 BigInteger div 無し inv使用
function binomialBig(n, k: integer): BigInteger;
//var
// r : integer;
begin
// r := min(k, n - k);
// result := fact[n] * fact_inv[r] * fact_inv[n - r] mod modbig; // 値が大きくなるので不利
result := fact[n] * (fact_inv[k] * fact_inv[n - k] mod modbig) mod modbig;
end;
// オイラーNo入力処理 big
function TForm1.NinputBig(var n: integer): boolean;
var
c : integer;
begin
result := true;
val(labelededit2.Text, n, c);
if c <> 0 then begin
memo1.Text := 'オイラーNo に間違いがあります。';
result := false;
exit;
end;
if n < 0 then begin
memo1.Text := 'オイラーNoはゼロ以上にして下さい。';
result := false;
end;
if n > NB then begin
memo1.Text := 'オイラーNo が大きすぎます' + intTostr(NB) + '迄です。';
result := false;
end;
end;
// オイラー数 BigInteger
procedure TForm1.BigIntegerBtnClick(Sender: TObject);
label
N0;
var
n, n2, nd2 : integer;
En : array of BigInteger;
i, k, k2 : integer;
s : BigInteger;
mstr : string;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
begin
if not NinputBig(n) then exit; // n数入力
Int64Btn.Enabled := false;
BigIntegerBtn.Enabled := false;
StopWatch := TStopwatch.StartNew;
memo1.Clear;
if n > 0 then
case RadioGroup1.ItemIndex of
0: factmbigake(n); // !テーブル
1: init_nck(n); // inv配列
2: calac_com(n); // nCk nk配列
end;
nd2 := n div 2;
setlength(En, nd2 + 1); // No=0 + 偶数No用配列確保
i := 0; // Kn [0] [1] [2] [3] [4] [5] [6]・・
En[i] := 1; // En 0 2 4 6 8 10 12・・
if nd2 < 100 then memo1.Lines.Append('E' + intTostr(i) + ' = ' + En[i].ToString);
if n = 0 then goto N0;
for i := 1 to nd2 do begin // for i = 2 to n step 2
application.ProcessMessages;
s := 0;
n2 := i shl 1; // n2 = i * 2
for k := 0 to i - 1 do begin // ΣEk
k2 := k shl 1;
case RadioGroup1.ItemIndex of // k2 = k * 2
0: s := s + binomialBigB(n2, k2) * En[k]; // !テーブル
1: s := s + binomialBig(n2, k2) * En[k]; // inv配列
2: begin // 二項配列の対称性利用
if k2 <= i then // k <= n / 2
s := s + com[n2, k2] * En[k] // nCk nk配列
else // k > n / 2
s := s + com[n2, n2 - k2] * En[k]; // nCk nk配列
end;
end;
end;
En[i] := -s; // En[No/2] = -s
if (nd2 = i) or (i <= 20) then begin
if s > 0 then mstr := ' = '
else mstr := ' = ';
if (i <= 20) and (nd2 < 100) then
memo1.Lines.Append('E' + intTostr(n2) + mstr + En[i].ToString);
if (nd2 = i) and (i > 20) then begin
if nd2 < 100 then Memo1.Lines.Append('');
memo1.Text := memo1.Text + 'E' + intTostr(n2) + mstr + En[i].ToString;
end;
end;
end;
N0:
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
Edit1.text := '演算時間 = ' + intTostr(ElapsedMillseconds) + 'msec';
Int64Btn.Enabled := True;;
BigIntegerBtn.Enabled := true;
end;
//----------------------------- 初期設定 ---------------------------------------
procedure TForm1.FormCreate(Sender: TObject);
begin
labeledEdit1.EditLabel.Caption := 'En n<=' + intTostr(NI);
labeledEdit2.EditLabel.Caption := 'En n<=' + intTostr(NB);
end;
end.
Euler_numbers_4.zip
各種プログラム計算例に戻る