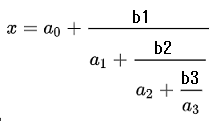
連分数
連分数は分母に更に分数が含まれているような分数です。
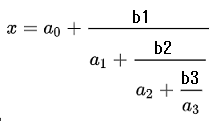
分子の値が全て1の場合正則連分数と呼ばれます。
表記方法としては次のようなものもあります。
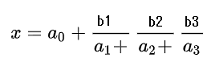
連分数で、πの値や、三角関数、平方根の値を表すことができ、小数点を含む実数を簡単に連分数に変換することが出来ます。
詳細については、webで"連分数"を検索してください。
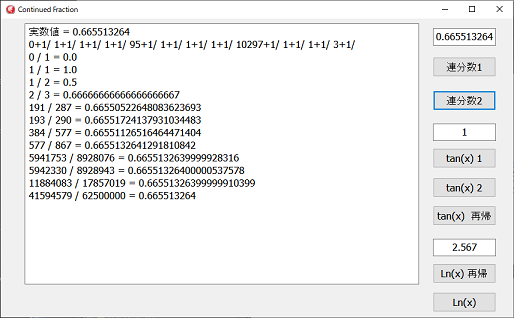左図は、実数値を連分数に変換した場合の実行例です。
三角関数値としては、tan(x)を取り上げています。
big_mathでは、tan(x)を級数展開で求めていますが、連分数による方法の方が高速なのかもしれません。
プログラム
Bigdecimalの組み込みはベルヌーイ数 その4を参照して下さい。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls;
type
TForm1 = class(TForm)
Memo1: TMemo;
continued_fraction_btn1: TButton;
Edit1: TEdit;
Edit2: TEdit;
tanx2_btn: TButton;
continued_fraction_btn2: TButton;
Tanx3_btn: TButton;
tanx1_btn: TButton;
Edit3: TEdit;
LnX1_Btn: TButton;
LnX2_btn: TButton;
procedure continued_fraction_btn1Click(Sender: TObject);
procedure tanx2_btnClick(Sender: TObject);
procedure continued_fraction_btn2Click(Sender: TObject);
procedure Tanx3_btnClick(Sender: TObject);
procedure tanx1_btnClick(Sender: TObject);
procedure LnX1_BtnClick(Sender: TObject);
procedure LnX2_btnClick(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses Velthuis.Bigdecimals, Velthuis.BigIntegers, math;
//--------------------------------------------------------------
// tanの連分数展開計算
// tan(x) x radian
// tan(x) = x /
// 1 - x^2 /
// 3 - x^2 / 5,7,9
procedure TForm1.tanx1_btnClick(Sender: TObject);
const
N = 15;
var
i : integer;
x, t : double;
c, b : array[0..N - 1] of double;
// tan(x)
function ascend(n: integer): double;
var
f, bk : double;
k : integer;
begin
bk := 0;
f := 0; // 初期値
for k := n downto 0 do begin // 後ろから計算
bk := b[k] + f;
if bk = 0 then break;
f := c[k] / bk;
end;
if bk = 0 then result := infinity
else result := f;
end;
begin
val(edit2.Text, x, i);
if i <> 0 then begin
application.MessageBox('入力値に間違いが有ります。','注意',0);
exit;
end;
memo1.Clear;
c[0] := x;
for i := 1 to N - 1 do c[i] := -x * x; // x, -x^2, -x^2, ・・・
for i := 0 to N - 1 do b[i] := 2 * (i + 1) - 1; // 1, 3, 5, 7, ・・・ 奇数
t := ascend(N - 1); // 連分数計算
Memo1.Lines.Append('tan(x) = ' + floattostr(t));
end;
// tan(x)
// 途中結果出力あり
procedure TForm1.tanx2_btnClick(Sender: TObject);
const
N = 18;
var
i : integer;
x, t : double;
// tan(x) 計算途中経過出力あり
function descend(x: double; n: integer): double;
var
i : integer;
p1, q1, p2, q2, p3, q3 : double;
ci, bi, p2b : double;
begin
p1 := 1; // 初期値 分子1
q1 := 0; // 初期値 分母1
p2 := 0; // 初期値 分子2
q2 := 1; // 初期値 分母2
p2b := 0;
for i := 1 to n do begin // 先頭から計算
if i = 1 then ci := x // ci= x, -x^2, -x^2 ・・・
else ci := -x * x;
bi := 2 * i - 1; // bi= 1,3,5,7,9・・・奇数
p3 := p1 * ci + p2 * bi; // 分子計算
p1 := p2;
p2 := p3;
q3 := q1 * ci + q2 * bi; // 分母計算
q1 := q2;
q2 := q3;
if q2 <> 0 then begin // 分母がゼロでなければ
p1 := p1 / q2;
q1 := q1 / q2;
p2 := p2 / q2;
q2 := 1;
Form1.Memo1.Lines.Append(inttostr(i) + ': ' + floattostr(p2));
if p2b = p2 then break; // 同じ値が続いたら終了
p2b := p2;
end
else begin // 分母がゼロだったら
Form1.Memo1.Lines.Append('無限大');
break;
end;
end;
if q2 <> 0 then result := p2 else result := infinity;
end;
begin
val(edit2.Text, x, i);
if i <> 0 then begin
application.MessageBox('入力値に間違いが有ります。','注意',0);
exit;
end;
memo1.Clear;
t := descend(x, N); // 途中結果出力あり計算
Memo1.Lines.Append('tan(x) =' + floattostr(t));
end;
// tan(x) 再帰ループ計算
procedure TForm1.Tanx3_btnClick(Sender: TObject);
var
x, t : double;
ch : integer;
// x radian
// x2 x^2
// t 連分数
// n 再起数 nの1/2 n は奇数
function drTan(x, x2, t: double; n: integer): double;
begin
if n - t = 0 then t := infinity
else t := x2 / (n - t);
n := n - 2;
if (n <= 1) then begin
if (1 - t) = 0 then result := infinity
else result := x / (1 - t);
end
else
result := drTan(x, x2, t, n);
end;
begin
val(edit2.Text, x, ch);
if ch <> 0 then begin
application.MessageBox('入力値に間違いが有ります。','注意',0);
exit;
end;
memo1.Clear;
t := drtan(x, x * x, 0, 21); // 再起計算
Memo1.Lines.Append('再帰ループ計算');
Memo1.Lines.Append('tan(x) =' + floattostr(t));
end;
//-------------------------------------------------------------------------
// ln(x)
// ln(1+x) = x/
// 1+x/
// 2+x/
// 3+2x/
// 2+2x/
// 5+3x/
// 2+3x/
// 7+ ・・・
procedure TForm1.LnX1_BtnClick(Sender: TObject);
const
N = 28;
var
xin, x : double;
ch : integer;
t, Lnx : double;
// 対数関数 再帰 後ろから計算
function drLog(x: double; n: integer; t: double): double;
var
n2 :Integer;
x2 :double;
begin
n2 := n;
x2 := x;
if (n > 3) then
begin
if (n mod 2 = 0) then n2 := 2;
x2 := x * (n div 2);
end;
t := x2 / (n2 + t);
if (n <= 2) then result := x / (1 + t)
else result := drLog(x, n - 1, t);
end;
begin
val(edit3.Text, xin, ch); // 入力値確認
if ch <> 0 then begin
application.MessageBox('入力値に間違いが有ります。','注意',0);
exit;
end;
if xin <= 0 then begin
application.MessageBox('無効な入力です。','注意',0);
exit;
end;
Memo1.Clear;
t := 0;
x := xin - 1;
LnX := drLog(x, n, t);
Memo1.Lines.Append('再帰計算');
Memo1.Lines.Append('Len(x) =' + floattostr(Lnx));
end;
// ln(x)
// ln(1+x) = x/
// 1+1^2x/
// 2+1^2x/
// 3+2^2/
// 4+2^2/
// 5+3^2x/
// 6+3^2x/
// 7+4^2/
// 8+4^2/
// 9+ ・・・・・
procedure TForm1.LnX2_btnClick(Sender: TObject);
const
N = 28;
var
xin : double;
ch : integer;
Lnx : double;
// ln(x)
function drln(x: double; n: integer): double;
var
nx, i : integer;
t : double;
begin
t := 0;
for i := n downto 2 do begin // n -> 2 後ろから計算
nx := i div 2;
t := nx * nx * x / (i + t)
end;
result := x / (1 + t); // n=1
end;
begin
val(edit3.Text, xin, ch); // 入力値確認
if ch <> 0 then begin
application.MessageBox('入力値に間違いが有ります。','注意',0);
exit;
end;
if xin <= 0 then begin
application.MessageBox('無効な入力です。','注意',0);
exit;
end;
Memo1.Clear;
Lnx := drln(xin - 1, 28);
Memo1.Lines.Append('Len(x) =' + floattostr(Lnx));
end;
//-------------------------------------------------------------------------
// 実数の連分数
procedure TForm1.continued_fraction_btn1Click(Sender: TObject);
var
xin : double;
x, b, a, t, one : bigdecimal;
ch : integer;
begin
val(edit1.Text, xin, ch); // 入力値確認
if ch <> 0 then begin
application.MessageBox('入力値に間違いが有ります。','注意',0);
exit;
end;
memo1.Clear;
memo1.Lines.Append('実数値 = ' + floattostr(xin));
x := edit1.Text;
b := x;
t := '1e-30'; // 収束判定値
one := '1';
while True do begin
a := b.Int; // 小数部切り捨て
memo1.Lines.Append(a.ToPlainString + '+1/');
b := b - a; // 小数部のみ取り出し
if bigdecimal.Abs(b) < t then break;
b := one / b;
end;
end;
// 実数の連分数
procedure TForm1.continued_fraction_btn2Click(Sender: TObject);
var
a : array of bigdecimal; // 連分数
t : array of array of bigdecimal; // 分数 分子分母
xb : bigdecimal;
k : integer;
s : string;
xin : double;
procedure ContFrac(x : bigdecimal); // 連分数計算
const
M = 32; // 最大ループ数
var
b, one, h : bigdecimal;
i : integer;
begin
one := '1';
h := '1e-30'; // 収束判定値
for i := 1 to M do begin
b := x.Int; // 小数点以下切り捨て
setlength(a, i);
a[i - 1] := b; // 連分数 配列a
x := x - b; // xの小数部
if bigdecimal.Abs(x) < h then break;
x := one / x;
end;
end;
procedure ApproximateRatio; // 近似分数(比)計算 分子 & 分母
var
p0, p1, p2 : bigdecimal;
q0, q1, q2 : bigdecimal;
one : bigdecimal;
i, j, k : integer;
begin
one := '1';
p0 := a[0]; // 分子
q0 := one; // 分母
p1 := a[1] * p0 + one;
q1 := a[1];
j := length(a);
setlength(t, j, 2);
t[0, 0] := p0; // 分子
t[0, 1] := q0; // 分母
t[1, 0] := p1;
t[1, 1] := q1;
delete(a, 0 , 2); // 配列a 先頭2個削除
j := length(a);
for k := 0 to j - 1 do begin
p2 := a[k] * p1 + p0; // 分子
q2 := a[k] * q1 + q0; // 分母
i := k + 2;
t[i, 0] := p2; // 分子
t[i, 1] := q2; // 分母
p0 := p1;
p1 := p2;
q0 := q1;
q1 := q2;
end;
end;
begin
val(edit1.Text, xin, k); // 入力値確認
if k <> 0 then begin
application.MessageBox('入力値に間違いが有ります。','注意',0);
exit;
end;
Memo1.Clear;
memo1.Lines.Append('実数値 = ' + floattostr(xin));
xb := edit1.Text;
ContFrac(xb); // 連分数計算 結果配列a
s := '';
for xb in a do s := s + xb.ToPlainString + '+1/ ';
memo1.Lines.Append(s);
ApproximateRatio; // 連分数から分数 分子分母計算 結果配列t
for k := 0 to length(t) - 1 do begin
if t[k, 0] <> bigdecimal.Zero then begin // ゼロ表示'0.0'の為ゼロ以外表示調整
xb := t[k, 0] / t[k, 1];
xb := xb.RoundToScale(20, rmNearestUp); // 小数点以下20桁で丸め
xb := xb.RemoveTrailingZeros(1); // 不要なゼロ削除
s := xb.ToPlainString;
end
else s := '0.0';
memo1.Lines.Append(t[k, 0].ToPlainString +' / ' + t[k, 1].ToPlainString + ' = ' + s);
end;
end;
end.
continued_fraction.zip
三角関数、逆三角関数、その他関数 に戻る