プログラムでは、正則ベータ関数を利用して、累積確率を計算している例と、正則ベータ関数を使わずに、確率密度を加算して累積確率を計算している計算例があります。
正則ベータ関数は不完全ベータ関数を参照して下さい。二項分布
不完全ベーター関数計算の利用に二項分布の計算があります。
詳細は、ウィキペディア 二項分布 を参照してください。
プログラムでは、正則ベータ関数を利用して、累積確率を計算している例と、正則ベータ関数を使わずに、確率密度を加算して累積確率を計算している計算例があります。
正則ベータ関数は不完全ベータ関数を参照して下さい。
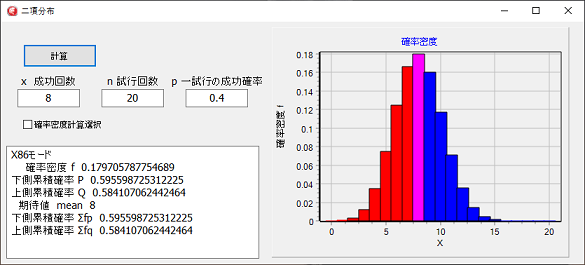累積確率で∑fp、∑fqとなっているのは、確率密度を加算して計算したものです。
正則ベータ関数を利用して計算したものと値があうのか確認しています。
プログラムは Ｃ言語辞典 アルゴリズム にあるものを Delphi ように変換し、更に別の計算を追加してあります。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, Vcl.StdCtrls, Vcl.ExtCtrls,
VCLTee.Series, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart, system.UITypes, system.Math;
type
TForm1 = class(TForm)
Chart1: TChart;
Memo1: TMemo;
LabeledEdit2: TLabeledEdit;
LabeledEdit1: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
Button1: TButton;
Series1: TBarSeries;
CheckBox1: TCheckBox;
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
// ************ loggamma(x) ************
const
N = 8;
B0 = 1; // 以下はBernoulli数
B1 = (-1.0 / 2.0);
B2 = ( 1.0 / 6.0);
B4 = (-1.0 / 30.0);
B6 = ( 1.0 / 42.0);
B8 = (-1.0 / 30.0);
B10 = ( 5.0 / 66.0);
B12 = (-691.0 / 2730.0);
B14 = ( 7.0 / 6.0);
B16 = (-3617.0 / 510.0);
function loggamma(x : double): double; // ガンマ関数の対数
var
LOG_2PI : Double;
v, w : Double;
begin
v := 1;
while x < N do begin
v := v * x;
x := x + 1;
end;
LOG_2PI := ln(2 * pi);
w := 1 / (x * x);
result := ((((((((B16 / (16 * 15)) * w + (B14 / (14 * 13))) * w
+ (B12 / (12 * 11))) * w + (B10 / (10 * 9))) * w
+ (B8 / ( 8 * 7))) * w + (B6 / ( 6 * 5))) * w
+ (B4 / ( 4 * 3))) * w + (B2 / ( 2 * 1))) / x
+ 0.5 * LOG_2PI - ln(v) - x + (x - 0.5) * ln(x);
end;
// 正則ベータ関数
function p_beta(x, a, b : double): double;
var
k : integer;
p1, q1, p2, q2, d, previous : double;
begin
if a <= 0 then begin
result := MaxDouble;
exit;
end;
if b <= 0 then begin
if x < 1 then begin
result := 0;
exit;
end;
if x = 1 then begin
result := 1;
exit;
end;
result := MaxDouble;
exit;
end;
if x > (a + 1) / (a + b + 2) then begin
result := 1 - p_beta(1 - x, b, a);
exit;
end;
if x <= 0 then begin
result := 0;
exit;
end;
p1 := 0;
q1 := 1;
p2 := exp(a * ln(x) + b * ln(1 - x)
+ loggamma(a + b) - loggamma(a) - loggamma(b)) / a;
q2 := 1;
k := 0;
while k < 200 do begin
previous := p2;
d := - (a + k) * (a + b + k) * x
/ ((a + 2 * k) * (a + 2 * k + 1));
p1 := p1 * d + p2;
q1 := q1 * d + q2;
inc(k);
d := k * (b - k) * x / ((a + 2 * k - 1) * (a + 2 * k));
p2 := p2 * d + p1;
q2 := q2 * d + q1;
if q2 = 0 then begin
p2 := Maxdouble;
continue;
end;
p1 := p1 / q2;
q1 := q1 / q2;
p2 := p2 / q2;
q2 := 1;
if p2 = previous then begin
result := p2;
exit;
end;
end;
Form1.Memo1.Lines.Add('p_beta: 収束しません');
result := p2;
end;
function q_beta(x, a, b: double): double;
begin
result := 1 - p_beta(x, a, b);
end;
//**********************************************************
// 2項分布 B(n,p) の X <= k の確率
function p_binomial(n: integer; p: double; k: integer): double;
begin
if k < 0 then begin
result := 0;
exit;
end;
if k >= n then begin
result := 1;
exit;
end;
result := p_beta(1 - p, n - k, k + 1);
end;
// 2項分布 B(n,p) の X >= k の確率
function q_binomial(n: integer; p: double; k: integer): double;
begin
if k <= 0 then begin
result := 1;
exit;
end;
if k > n then begin
result := 0;
exit;
end;
result := p_beta(p, k, n - k + 1);
end;
//**********************************************************
// 2項分布 確率密度1
function binomial_mass(n: integer; p: double; k: integer): double;
var
nCx: double;
begin
nCx := exp(loggamma(n + 1) - loggamma(k + 1) - loggamma(n - k + 1));
result := nCx * power(p, k) * power(1 - p, n - k);
end;
// 2項分布 確率密度2
function binomial_f(n: integer; p: double; k: integer): double;
var
q : double;
t : double;
i : integer;
begin
q := 1 - p;
t := power(q, n);
for i := 0 to k - 1 do
t := t * (n - i) * p / ((i + 1) * q);
result := t;
end;
//**********************************************************/
procedure TForm1.Button1Click(Sender: TObject);
var
ch : integer;
n, x : integer; // n 試行回数 x 成功回数
p : double; // p 一試行の成功確率
Po, Qo : double;
fo: double;
I: Integer;
begin
val(LabeledEdit1.Text, n, Ch);
if ch <> 0 then begin
MessageDlg('n値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
if n <= 0 then begin
MessageDlg('nの値をゼロより大きくしてください。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
val(LabeledEdit2.Text, p, Ch);
if ch <> 0 then begin
MessageDlg('p値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
if p < 0 then begin
MessageDlg('pの値がゼロ以下です。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
if p > 1 then begin
MessageDlg('pの値をが１より大きいです。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
val(LabeledEdit3.Text, x, Ch);
if ch <> 0 then begin
MessageDlg('x値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
if x < 0 then begin
MessageDlg('xの値がゼロ以下です。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
if x > n then begin
MessageDlg('xの値がnより大きいです。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
Memo1.Clear;
{$IFDEF CPUX64} // プラットフォーム64ビット
begin
Memo1.Lines.Add('X64モード');
end;
{$ENDIF CPUX64}
{$IFDEF CPUX86} // プラットフォーム32ビット
begin
Memo1.Lines.Add('X86モード');
end;
{$ENDIF CPUX86}
if power(1 - p, n) = 0 then begin // 確率密度計算桁落ち確認
MessageDlg('n か p が大きすぎます。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
Po := p_binomial(n, p, x);
Qo := q_binomial(n, p, x);
if checkbox1.Checked = true then
fo := binomial_f(n, p, x)
else
fo := binomial_mass(n, p, x);
Memo1.Lines.Add(' 確率密度 f ' + floatTostr(fo));
Memo1.Lines.Add('下側累積確率 P ' + floatTostr(Po));
Memo1.Lines.Add('上側累積確率 Q ' + floatTostr(Qo));
Memo1.Lines.Add(' 期待値 mean ' + floatTostr(n * p));
Po := 0;
Qo := 0;
Series1.Clear;
for I := 0 to n do begin
if checkbox1.Checked = true then
fo := binomial_f(n, p, I)
else
fo := binomial_mass(n, p, I);
if I < x then begin
Series1.AddXY(I, fo, '', clred);
Po := Po + fo;
end;
if I = x then begin
Series1.AddXY(I, fo, '', clFuchsia);
Po := Po + fo;
Qo := Qo + fo;
end;
if I > x then begin
Series1.AddXY(I, fo, '', clBlue);
Qo := Qo + fo;
end;
end;
Memo1.Lines.Add('下側累積確率 Σfp ' + floatTostr(Po));
Memo1.Lines.Add('上側累積確率 Σfq ' + floatTostr(Qo));
end;
end.
binomial_distribution_function.zip