不完全ベータ関数

 
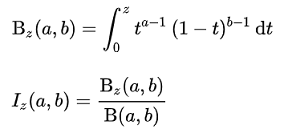
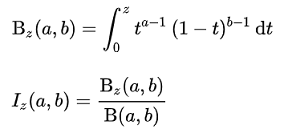
　不完全ベータ関数 Ｂｚ は、ベータ関数の積分の範囲を限定したものです、不完全ガンマ関数はガンマ関数の積分範囲を限定したものでした。
積分の範囲は ０ ≦ ｚ ≦ １　となります。
　Ｉｚ は正則ベータ関数で、全体の積分値に対しての積分割合を示しています。
Z = 1　で全ての積分値となるので、Ｉｚ　は　１　となります。

　不完全ベータ関数は、不完全ガンマ関数と同じように、単体での利用はあまりなく、確率の計算に応用されています。

詳細については、ウィキペディア　不完全ベータ関数　を参照して下さい。

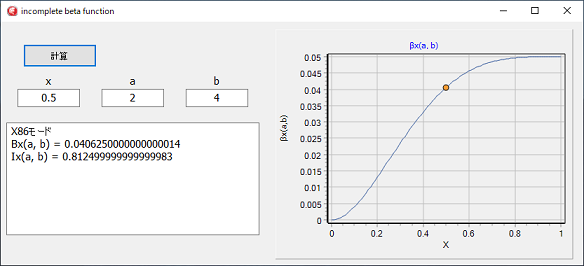
　次のプログラムは、Mathematics Source Library C & ASM にあるC 言語のものをDelphiに変換したものです。
このプログラムは長いので、短いプログラムの　Ｃ言語辞典　アルゴリズム　にあるものを　Delphi　に変換したものを後に載せておきます。

不完全ベータ関数　プログラム　１

//=============================================================================
// http://www.mymathlib.com/c_source/functions/gamma_beta/gamma_function.c
// http://www.mymathlib.com/c_source/functions/gamma_beta/beta_function.c
// http://www.mymathlib.com/c_source/functions/gamma_beta/incomplete_beta_function.c
//
// ルーチン
//  Gamma_Function
//  xGamma_Function
//  Gamma_Function_Max_Arg
//  xGamma_Function_Max_Arg
//  Ln_Gamma_Function(x)
//  xLn_Gamma_Function(x)
//  Beta_Function
//  xBeta_Function
//  Ln_Beta_Function
//  xLn_Beta_Function
//  Incomplete_Beta_Function
//  xIncomplete_Beta_Function
//
// 実数x> 0のxのガンマ関数は次のように定義されます。
// Gamma(x)= Integral[0、inf]t^(x-1)exp(-t)dt
// 複雑な平面内で解析的に継続され、単純な極がある
// 非正の整数、つまりガンマ関数は有理型である
// 非正の整数に単純な極を持つ関数。
// 実数x<0の場合、ガンマ関数は反射方程式を満たします。
// Gamma(x)= pi/(sin(pi*x)*Gamma(1-x))
//
// 関数Gamma_Function()およびxGamma_Function()はガンマを返します。
// 関数はxでx実数で評価されます。
//
// 関数Gamma_Function_Max_Arg()は、最大引数を返します
// 引数>1のガンマ関数は、double型の値を返します。
//
// 関数xGamma_Function_Max_Arg()は、
// 引数>1のガンマ関数とextended型の戻り値です。
//
// Ln_Gamma_Function(x) および　xLn_Gamma_Function(x)
//　
// Gamma_Function_Max_Arg = 171とすると、
// 0 < x <= 171の場合、ln(gamma(x))は、Gamma_Function(x)からの結果。
// x> 171の場合、ln(gamma(x)は漸近展開を使用して計算されます。
// ln(gamma(x)〜ln(2sqrt(2pi))-x + (x-1/2)ln x +
// B[2j] / [2j *(2j-1)* x^(2j-1)]の合計、
// 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。
//
// ベータ関数は被積分関数の0から1までの積分です
// x^(a-1)(1-x)^(b-1)、パラメータa>0およびb>0
// ガンマ関数に対して、ベータ関数は次のとおりです：
// beta(a,b)= gamma(a)*gamma(b)/gamma(a+b)
//
// Ln_Beta_Function 及び xLn_Beta_Function
// ln(Beta(a、b)=ln(Gamma(a))+ln(Gamma(b))-ln(Gamma(a+b))
//
// incomplete_beta_function
// 不完全なベータ関数は0からxまでの積分です
// t^(a-1)(1-t)^(b-1)dt,
// 0<=x<=1、a>0 および b>0です。
//=============================================================================

unit Main;

interface

uses
  Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
  Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, VclTee.TeeGDIPlus,
  VCLTee.TeEngine, VCLTee.Series, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart,
  system.UITypes;

type
  TForm1 = class(TForm)
    Button1: TButton;
    LabeledEdit2: TLabeledEdit;
    Memo1: TMemo;
    LabeledEdit1: TLabeledEdit;
    LabeledEdit3: TLabeledEdit;
    Chart1: TChart;
    Series1: TLineSeries;
    Series2: TPointSeries;
    procedure Button1Click(Sender: TObject);
    procedure FormCreate(Sender: TObject);
  private
    { Private 宣言 }
    function Gamma_Function(x: double): double;
    function xGamma_Function(x: extended): extended;
    function xGamma(x: extended): extended;
    function Duplication_Formula(two_x: extended): extended;
    function Gamma_Function_Max_Arg: double;
    function xGamma_Function_Max_Arg: extended;
    function Ln_Gamma_Function(x: double): double;
    function xLn_Gamma_Function(x: extended): extended;
    function xLnGamma_Asymptotic_Expansion(x: extended): extended;
    function Beta_Function(a, b: double): double;
    function xBeta_Function(a, b: extended): extended;
    function LnBeta_Function(a, b: double): double;
    function xLnBeta_Function(a, b: extended): extended;
    function Incomplete_Beta_Function(x, a, b: double): double;
    function xIncomplete_Beta_Function(x, a, b: extended): extended;
    function Beta_Continued_Fraction(x, a, b: extended): extended;
  Public
    { Public 宣言 }
  end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

uses math;

const
  LONG_MAX = 2147483647;
  e =  2.71828182845904523536028747;
  exp_g_o_sqrt_2pi = 6.23316569877722552586386e+3;
  g =  9.65657815377331589457187;
  max_double_arg: double  = 171.6243769;
  max_long_double_arg: extended = 1755.5;
  a: array[0..8] of extended = (
                                +1.14400529453851095667309e+4,
                                -3.23988020152318335053598e+4,
                                +3.50514523505571666566083e+4,
                                -1.81641309541260702610647e+4,
                                +4.63232990536666818409138e+3,
                                -5.36976777703356780555748e+2,
                                +2.28754473395181007645155e+1,
                                -2.17925748738865115560082e-1,
                                +1.08314836272589368860689e-4
                               );

//=============================================================================
//
// この関数はLanczosの式を使用して実際のGamma(x)を計算します。
// xの範囲は -(max_double_arg-1) < x < max_double_arg。
// ガンマ関数は複素平面で有理型であり、
// 正でない整数の値、xaの正の整数または半分の正の整数をテストすると、
// 約1.9e-16の最大絶対相対誤差です。
// x > max_double_argの場合、xGamma_Function(x)を使用する必要があります。
// または lnGamma(x) を計算します。
// x < 0の場合、ln(Gamma(x))は複素数になる可能性があることに注意してください。
// 複素数の計算はプログラムに組んでありません
// 戻り値
//   xが正で、max_double_argより小さい場合、Gamma(x)は
//   返され、x> max_double_argの場合、maxdoubleが返されます。
//   xが非正の整数、つまりxが極の場合、maxdoubleが返されます。
//  （Gamma(x)は極の両側で符号を変更することに注意してください）。
//   xが非正の非整数の場合　Gamma(x)> maxdouble場合、maxdoubleが返され、
//   Gamma(x)<-maxdoubleの場合、-maxdoubleが返されます。
//
//=============================================================================
//================ ガンマ関数 ===================
// Γ(x)
function TForm1.Gamma_Function(x: double): double;
var
  g: extended;
  maxx: double;
begin
  maxx := max_double_arg;
  if x >= maxx then begin
    result := maxdouble;
    exit;
  end;
  g := xGamma_Function(x);
  if abs(g) < maxdouble then
    result := g
  else
    if g < 0 then result := -maxdouble
             else result := maxdouble;
end;

//=============================================================================
//
// この関数はLanczosの式を使用して実際のGamma(x)を計算します。
// xの範囲は -(max_long_double_arg-1) < x < max_long_double_arg。
// ガンマ関数は複素平面で有理型であり、正でない整数の値
// xaの正の整数または半分の正の整数をテストすると、
// 最大絶対相対誤差は約3.5e-16です。
//
// x > max_long_double_argの場合、lnGamma(x)を使用する必要があります。
// x < 0 の場合、ln(Gamma(x)) は複素数になる可能性があることに注意してください。
//
// 戻り値
//  xが正で、max_long_double_argより小さい場合、Gamma(x)
//  が返され、x > max_long_double_argの場合、maxextendedが返されます。
//  xが正でない整数の場合、maxextendedが
//  返されます（Gamma(x)は値の両側で符号を変更することに注意してください）。
//  xが非正の非整数の場合でx>-(max_long_double_arg + 1）の場合
//  Gamma(x)が返されます。それ以外の場合は0.0が返されます
//
//=============================================================================
function TForm1.xGamma_Function(x: extended): extended;
var
  sin_x: extended;
  rg: extended;
  ix: int64;
begin
  if x > 0 then
    if x <= max_long_double_arg then begin
      result := xGamma(x);
      exit;
    end
    else begin
      result := maxextended;
      exit;
    end;
  if x > -LONG_MAX then begin
    ix := round(x);
    if x = ix then begin
      result := maxextended;
      exit;
    end;
  end;
  sin_x := sin(pi * x);
  if sin_x = 0 then begin
    result := maxextended;
    exit;
  end;
  if x < - max_long_double_arg - 1 then begin
    result := 0;
    exit;
  end;
  rg := xGamma(1 - x) * sin_x / pi;
  if rg <> 0 then result := 1 / rg
             else result := maxextended;
end;

//=============================================================================
//
// この関数はLanczosの式を使用して実際のGamma(x)を計算します。
// x、ここで0<x<=900。900<x<1755.5の場合、倍数公式を使用します。
// 関数power()。結果の相対誤差は約10^-16です。x = 0付近を除きます。
// x>1755.5の場合、lnGamma(x)を計算する必要があります。
// xが正で1755.5未満の場合、Gamma(x)が返され、
// x>1755.5の場合、maxextendedが返されます。
//
//=============================================================================
function TForm1.xGamma(x: extended): extended;
var
  xx: extended;
  temp: extended;
  n, i: integer;
  xx2 : extended;
begin
  if x < 1 then xx := x + 1 else xx := x;
  n := sizeof(a) div sizeof(extended);
  if x > max_long_double_arg then begin
    result := maxextended;
    exit;
  end;
  if x > 900 then begin
    result := Duplication_Formula(x);
    exit;
  end;
  temp := 0;
  for i := n - 1 downto 0 do temp := temp + a[i] / (xx + i);
  temp := temp + 1;
  xx2 := (xx - 0.5) / 2;
  temp := temp * (power((g + xx - 0.5) / e, xx2) / exp_g_o_sqrt_2pi );
  temp := temp * power((g + xx - 0.5) / e, xx2);      // X64 オーバーフロー対策
  if x < 1 then result := temp / x
           else result := temp;
end;

//=============================================================================
//
// この関数は倍数公式を使用してGamma(two_x)を返します。
//
//=============================================================================
function TForm1.Duplication_Formula(two_x: extended): extended;
var
  x: extended;
  g: extended;
  n: integer;
begin
  x := 0.5 * two_x;
  n := round(two_x) - 1;
  g := power(2.0, two_x - 1.0 - n);
  g := g * power(2, n);
  g := g / sqrt(pi);
  g := g * xGamma_Function(x);
  g := g * xGamma_Function(x + 0.5);
  result := g;
end;

//=============================================================================
//
// この関数は、Gamma_Functionの最大引数を返します。
// Gamma_Functionは引数が1より大きい場合、< maxdoubleという数値が返されます。
//
//=============================================================================
function TForm1.Gamma_Function_Max_Arg: double;
begin
  result := max_double_arg;
end;

//=============================================================================
//
// この関数は、xGamma_Functionの最大引数を返します。
// xGamma_Functionは引数が1より大きい場合、< maxextendedという数値が返されます。
//
//=============================================================================
function TForm1.xGamma_Function_Max_Arg: extended;
begin
 result := max_long_double_arg;
end;

//*****************************************************************************

//=============================================================================
//
// 正の実数xに対するGamma(x)の自然対数を計算します。
//
//=============================================================================

//=============================================================================
// Ln_Gamma_Function(x) および　xLn_Gamma_Function(x)
//　
// Gamma_Function_Max_Arg = 171とすると、
// 0 < x <= 171の場合、ln(gamma(x))は、Gamma_Function(x)からの結果。
// x> 171の場合、ln(gamma(x)は漸近展開を使用して計算されます。
// ln(gamma(x)〜ln(2sqrt(2pi))-x + (x-1/2)ln x +
// B[2j] / [2j *(2j-1)* x^(2j-1)]の合計、
// 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。
//
//=============================================================================
function TForm1.Ln_Gamma_Function(x: double): double;
begin
  // 正の引数の 0 <x <= Gamma_Function_Max_Arg
  // の場合、Log(Gamma(x)を返します。

  if x <= Gamma_Function_Max_Arg then result := ln(Gamma_Function(x))

  //そうでない場合は、ln Gamma(x) の漸近展開から結果を返します。
  else
   result := xLnGamma_Asymptotic_Expansion(x);
end;

//=============================================================================
//
// 正の実数のGamma(x)の自然対数を計算します
//
// Gamma_Function_Max_Arg = 171とすると、
// 0 <x <= 171の場合、ln(gamma(x))は
// Gamma_Function(x)からの結果の値。
// x> 171の場合、ln(gamma(x)) は漸近展開を使用して計算されます。
// ln（gamma(x))〜ln（2sqrt(2pi))-x +(x-1/2)ln x +
// B[2j] / [2j *(2j-1)* x^(2j-1)]の合計、
// 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。
//
//=============================================================================
function TForm1.xLn_Gamma_Function(x: extended): extended;
begin

  // 正の引数の場合、0 <x <= Gamma_Function_Max_Arg()
  // の場合、LogGamma(x)を返します。

  if x <= xGamma_Function_Max_Arg then result := ln(xGamma_Function(x))

  // そうでない場合は、ln Gamma(x) の漸近展開から結果を返します。
  else
    result := xLnGamma_Asymptotic_Expansion(x);
end;

//=============================================================================
//
// この関数は、漸近を評価することでlog(gamma(x)を推定します
//
// ln(Gamma(x))〜ln(2sqrt(2pi))-x +(x-1/2)ln(x) +
// B[2j] / [2j *（2j-1）* x^(2j-1)]の合計、
// 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。
//
//=============================================================================

const
  log_sqrt_2pi = 9.18938533204672741780329736e-1;

//ベルヌーイ数B(2)、B(4)、B(6)、...、B(20)現在B(2)、...、B(6)のみ

  B : array[0..9] of extended = ( 1.0 / (6 * 2 * 1),
                                 -1.0 / (30 * 4 * 3),
                                  1.0 / (42 * 6 * 5),
                                 -1.0 / (30 * 8 * 7),
                                  5.0 / (66 * 10 * 9),
                               -691.0 / (2730 * 12 * 11),
                                  7.0 / (6 * 14 * 13),
                              -3617.0 / (510 * 16 * 15),
                              43867.0 / (798 * 18 * 17),
                            -174611.0 / (330 * 20 * 19));

 n: integer = sizeof(B) div sizeof(extended);

function TForm1.xLnGamma_Asymptotic_Expansion(x: extended): extended;
//const
//  m = 3;                                // 3で十分な精度が得られます。
var
  i : integer;
  term: array[0..9] of extended;
  sum : extended;
  xx  : extended;
  xj  : extended;
  lngamma : extended;
begin
  sum := 0;
  xx := x * x;
  xj := x;
  lngamma := log_sqrt_2pi - xj + (xj - 0.5) * ln(xj);
  for i := 0 to  n - 1 do begin
//  for i := 0 to  m - 1 do begin
    term[i] := B[i] / xj;
    xj := xj * xx;
  end;
  for i := n - 1 downto 0 do sum := sum + term[i];
//  for i := m - 1 downto 0 do sum := sum + term[i];
  result := lngamma + sum;
end;
//*****************************************************************************

const
  ln_LDBL_MAX : extended =  1.13565234062941435e+4;

//==============================================================================
// function Beta_Function(a,b : double): double
//
// この関数は、beta(a、b)=gamma(a)*gamma(b)/gamma(a+b)、を返します
// ここでa> 0、b>0
//
// 戻り値
// beta（a、b）が返されます
// beta（a、b）がDBL_MAXを超える場合は、DBL_MAXが返されます
//==============================================================================

function TForm1.Beta_Function(a, b: double): double;
var
  beta : extended;
begin
  beta := xBeta_Function(a, b);
  if beta < MAXDouble then result := beta
                      else result := MAXDouble;
end;

//==============================================================================
// function xBeta_Function(a,b: extended): extended
//
//この関数は、beta(a,b)=gamma(a)*gamma(b)/gamma(a+b) を返します
// a> 0、b>0
//
// 引数
// ベータ関数の引数をextendedにします
// a,bは正でなければなりません
//
//戻り値
// beta（a、b）が返されます。//
// beta（a、b）がextendedを超える場合は、extendedが返されます
//
//==============================================================================

function TForm1.xBeta_Function(a, b: extended): extended;
var
  lnbeta : extended;
begin
  // If (a + b) <= Gamma_Function_Max_Arg() then simply return
  //  gamma(a)*gamma(b) / gamma(a+b).
  if (a + b) <= Gamma_Function_Max_Arg then begin
    result := xGamma_Function(a) / (xGamma_Function(a + b) / xGamma_Function(b));
    exit;
  end;
  // If (a + b) > Gamma_Function_Max_Arg() then simply return
  //  exp(lngamma(a) + lngamma(b) - lngamma(a+b) ).

   lnbeta := xLn_Gamma_Function(a) + xLn_Gamma_Function(b)
                                                 - xLn_Gamma_Function(a + b);
   if lnbeta > ln_LDBL_MAX then result := MAXExtended
                           else result := exp(lnbeta);
end;

//=============================================================================
// function Ln_Beta_Function(a,b: double): double;
//
// この関数は、ln(Beta(a,b))を返します
// ここで、a> 0およびb> 0です
//
// 戻り値
// log(beta(a、b))
//
//=============================================================================

function TForm1.LnBeta_Function(a, b: double): double;
begin
  result := xLnBeta_Function(a, b);
end;

//=============================================================================
// function xLn_Beta_Function(a,b: extended): extended;
//
// この関数は、ln(Beta(a,b))を返します
// ここで、a> 0およびb> 0です
//
// 戻り値
// log(beta(a、b))
//
//=============================================================================

function TForm1.xLnBeta_Function(a, b: extended): extended;
begin
  // If (a + b) <= Gamma_Function_Max_Arg then simply return
  //  log(gamma(a)*gamma(b) / gamma(a+b)).
  if a + b <= Gamma_Function_Max_Arg then begin
    if (a = 1.0) and (b = 1) then result := 0.0
    else result := ln( xGamma_Function(a) /
                             (xGamma_Function(a + b) / xGamma_Function(b)));
    exit;
  end;
  // If (a + b) > Gamma_Function_Max_Arg() then simply return
  //  lngamma(a) + lngamma(b) - lngamma(a+b).

  result := xLn_Gamma_Function(a) + xLn_Gamma_Function(b)
                                                  - xLn_Gamma_Function(a+b);
end;

//==============================================================================
// function Incomplete_Beta_Function(x,a,b: double): double;
//
// 不完全なベータ関数は0からxまでの積分です
// t^(a-1)(1-t)^(b-1)dt,
// 0 <= x <= 1, a>0 及び b>0です。
//
// 不完全なベータ関数を評価する手順では、関数の継続的な分数展開
// beta(x,a,b)=x^a*(1-x)^b/a*((1/1+)(d[1]/1+)(d[2]/1+） ...）
// ここでd[2m+1] = -(a+m)(a+b+m)x/((a+2m)(a+2m+1))
// d[2m]=m(bm)x/((a+2m)(a+2m-1)),
// 対称関係：
//  beta(x,a,b) = B(a,b)-beta(1-x,b,a）
//  B(a,b)は完全なベータ関数です。
// 繰り返し関係：
//  beta(x,a+1,b)= a/b beta(x,a,b+1)-x^a(1-x)^ b/b
//  beta(x,a,b+1)= b/a beta(x,a+1,b)+x^a(1-x)^ b/a
// 相互関係：
//  beta(x,a,b)= beta(x,a+1,b)+beta(x,a,b+1)
//
// a>1とb>1の両方の場合で
//  x<=(a-1)/(a+b-2）の場合,継続分数展開を使用します。
//  違う場合、対称関係を使用し、
//  beta(1-x,b,a）を評価するための拡張継続部分を使用します。
//
// a<1 および b>1 の場合
//  相互関係式を再帰と共に使用します
//  評価する関係
//  beta(x,a,b)= [(a+b)beta(x,a+1,b)+x^a(1-x)^b]/a
//
// a>1 かつ b<1 の場合
//  相互関係式を再帰と共に使用します
//  評価する関係
//  beta(x,a,b)= [(a+b)beta(x,a,b+1)-x^a(1-x)^b]/b
//
// a<1 および b<1の場合
//  相互関係式を使用して評価します
//  beta(x,a,b)= beta(x,a+1,b+beta(x,a,b+1)
//  1つの形状パラメータ> 1を持つベータ関数
//
// a=1 の場合、積分を明示的に評価します
// beta(x,a,b)=[1-(1-x)^b]/b
//
// b=1 の場合、積分を明示的に評価します
// beta(x,a,b)= x^a/a
//
// 引数
//  x 不完全なベータ関数積分の上限x、xは必須
//  a 不完全なベータ関数の正の形状パラメーター
//    a-1は、被積分関数の係数xの指数です
//  b 不完全なベータ関数の正のShapeパラメータ
//    b-1は、被積分関数の係数（1-x）の指数です
// 戻り値：
//  beta(x,a,b,がMAXDoubleを超える場合、MAXdoubleが返されます
//  そうでない場合は。beta(x,a,b)が返されます。
//==============================================================================

function TForm1.Incomplete_Beta_Function(x, a, b: double): double;
var
  beta : extended;
begin
  beta := xIncomplete_Beta_Function(x, a, b);
  if beta > MaxDouble then result := MaxDouble
                      else result := beta;
end;

function TForm1.xIncomplete_Beta_Function(x, a, b: extended): extended;
begin
  // Both shape parameters are strictly greater than 1
  if (a > 1.0) and (b > 1.0) then begin
    if x <= (a - 1.0) / (a + b - 2.0) then
         result := Beta_Continued_Fraction(x, a, b)
      else
         result := xBeta_Function(a, b)
                                   - Beta_Continued_Fraction(1 - x, b, a);
    exit;
  end;

  // Both shape parameters are strictly less than 1
  if (a < 1.0) and (b < 1.0) then begin
    result := xIncomplete_Beta_Function(x, a + 1, b)
                                  + xIncomplete_Beta_Function(x, a, b + 1);
    exit;
  end;

  // One of the shape parameters exactly equals 1
  if a = 1 then begin
    result := (1 - power(1 - x, b) ) / b;
    exit;
  end;
  if b = 1 then begin
    result := power(x, a) / a;
    exit;
  end;

  // Exactly one of the shape parameters is strictly less than 1.
  if a < 1  then begin
    result := ((a + b) * xIncomplete_Beta_Function(x, a + 1, b)
                                       + power(x, a) * power(1 - x, b) ) / a;
    exit;
  end;
  // The remaining condition is b < 1.0

  result := ((a + b) * xIncomplete_Beta_Function(x, a, b + 1)
                                       - power(x, a) * power(1 - x, b) ) / b;
end;

//==============================================================================
// function Beta_Continued_Fraction(x,a,b: extended): extended;
//
// 不完全なベータを評価するために使用される継続的な分数展開関数
//
// beta(x,a,b)= x^a*(1-x)^b/a*((1/1+)(d[1]/1+)(d[2]/1+） ...）
//        d[2m+1]=-(a+m)(a+b+m)x/((a+2m)(a+2m+1)
//        d[2m]  = m(bm)x/((a+2m)(a+2m-1))
//
//   a> 1,b> 1,及び x <=（a-1）/（a + b-2）です。
//
// 引数：
//  x 不完全ベータ関数積分の上限、x間隔[0,1]内にある必要があります
//  a 不完全なベータ関数のShapeパラメータ、a-1 被積分関数の係数xの指数です。
//  b 不完全なベータ関数のShapeパラメータ、b-1 被積分関数の係数（1-x）の指数です。
//==============================================================================

var
  LDBL_EPSILON : extended;

function TForm1.Beta_Continued_Fraction(x, a, b: extended): extended;
var
  Am1, Bm1: extended;
  A0, B0 : extended;
  e : extended;
  Ap1, Bp1 : extended;
  f_less: extended;
  f_greater : extended;
  m : integer;
  aj, am : extended;
  eps : extended;
  j, k : integer;
begin
  Am1 := 1.0;
  A0 := 0.0;
  Bm1 := 0.0;
  B0 := 1.0;
  e := 1.0;
  Ap1 := A0 + e * Am1;
  Bp1 := B0 + e * Bm1;
  f_less := Ap1 / Bp1;
  f_greater := 0.0;
  aj := a;
  eps := 10.0 * LDBL_EPSILON;
  j := 0;
  m := 0;
  k := 1;

  if x = 0  then  begin
    result := 0;
    exit;
  end;

  while (2 * abs(f_greater - f_less) > eps * abs(f_greater + f_less)) do begin
    Am1 := A0;
    A0 := Ap1;
    Bm1 := B0;
    B0 := Bp1;
    am := a + m;
    e := - am * (am + b) * x / ( (aj + 1) * aj );
    Ap1 := A0 + e * Am1;
    Bp1 := B0 + e * Bm1;
    k := (k + 1) and 3;
    if k = 1 then f_less := Ap1 / Bp1
             else
               if k = 3 then f_greater := Ap1/Bp1;
    if abs(Bp1) > 1.0 then begin
      Am1 := A0 / Bp1;
      A0 := Ap1 / Bp1;
      Bm1 := B0 / Bp1;
      B0 := 1.0;
    end
    else begin
      Am1 := A0;
      A0 := Ap1;
      Bm1 := B0;
      B0 := Bp1;
    end;
    inc(m);
    j := j + 2;
    aj := a + j;
    e := m * ( b - m ) * x / ( ( aj - 1) * aj  );
    Ap1 := A0 + e * Am1;
    Bp1 := B0 + e * Bm1;
    k := (k + 1) and 3;
    if k = 1 then f_less := Ap1 / Bp1
             else
              if k = 3 then f_greater := Ap1/Bp1;
  end;
  result := exp( a * ln(x) + b * ln(1 - x) + ln(Ap1 / Bp1) ) / a;
end;

//=============================================================================
// beta関数計算
// a, bの値は a>0 b>0 の範囲です。
// 入力されたa, b の値でbata関数を計算し、グラフのbata曲線上にプロットします。
//=============================================================================
procedure TForm1.Button1Click(Sender: TObject);
var
  ch   : integer;
  a, b, x : extended;
  Bx, Bi   : extended;
  dx, Bg: double;
  Sg   : string;
begin
  val(LabeledEdit1.Text, a, Ch);
  if ch <> 0 then begin
    MessageDlg('a値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  if a < 0 then begin
    MessageDlg('aの値をゼロより大きくしてください。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  val(LabeledEdit2.Text, b, Ch);
  if ch <> 0 then begin
    MessageDlg('b値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  if b < 0 then begin
    MessageDlg('bの値をゼロより大きくしてください。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  Memo1.Clear;
  val(LabeledEdit3.Text, x, Ch);
  if ch <> 0 then begin
    MessageDlg('x値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  if x < 0 then begin
    MessageDlg('xの値をゼロより大きくしてください。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  if x > 1 then begin
    MessageDlg('xの値をが１より大きいです。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;

  Memo1.Clear;
  {$IFDEF CPUX64}                               // プラットフォーム64ビット
  begin
    Memo1.Lines.Add('X64モード');
  end;
  {$ENDIF CPUX64}
  {$IFDEF CPUX86}                               // プラットフォーム32ビット
  begin
    Memo1.Lines.Add('X86モード');
  end;
  {$ENDIF CPUX86}
  if (a <= 0) or (b <= 0) then begin                  // X Y 0なら
    if a <= 0 then Memo1.Lines.Add('aの値をゼロより大きくしてください。');
    if b <= 0 then Memo1.Lines.Add('bの値をゼロより大きくしてください。');
    exit;
  end;
  Sg := 'Bx(a, b) = ';
  Bx := Incomplete_Beta_Function(x, a, b);
  Bi := Beta_Function(a, b);
  Memo1.Lines.Add(Sg + floatTostrF(Bx, ffgeneral, 20, 3));  // iBの値表示
  Sg := 'Ix(a, b) = ';
  Memo1.Lines.Add(Sg + floatTostrF(Bx / Bi, ffgeneral, 20, 3));  // iBの値表示
  Series1.Clear;
  Series2.Clear;
  Bg := Incomplete_Beta_Function(x, a, b);
  Series2.AddXY(X, Bg);
  dx := 1 / 100;
  for ch := 0 to 100 do begin
    X := dx * ch;
    Bg := Incomplete_Beta_Function(x, a, b);
    Series1.AddXY(X, Bg);
  end;
end;

//////////////////////////////////////////////////////////////////////
//
// LDBL_EPSILONの設定
// 
// １に加算して１以上になる一番小さい値を計算します
//////////////////////////////////////////////////////////////////////
procedure TForm1.FormCreate(Sender: TObject);
var
  i : integer;
  y, z : extended;
begin
  i := 0;
  z := 1;
  LDBL_EPSILON := 1;
  repeat
    LDBL_EPSILON := LDBL_EPSILON / 2;
    y := z + LDBL_EPSILON;
    inc(i);
  until (y = 1) or (i > 70);
  LDBL_EPSILON := LDBL_EPSILON * 2;
end;

end.

不完全ベータ関数　プログラム２

　ここのプログラムは、正則ベータ関数が基本計算になっています、不完全ベータ関数を直接計算するものではありません。
ベータ関数の値に正則ベータ関数の値を乗ずれば不完全ベーター関数の値になります。

unit Main;

interface

uses
  Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
  Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, Vcl.StdCtrls, Vcl.ExtCtrls,
  VCLTee.Series, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart, system.UITypes, system.Math;

type
  TForm1 = class(TForm)
    Chart1: TChart;
    Series1: TLineSeries;
    Series2: TPointSeries;
    Memo1: TMemo;
    LabeledEdit2: TLabeledEdit;
    LabeledEdit1: TLabeledEdit;
    LabeledEdit3: TLabeledEdit;
    Button1: TButton;
    procedure Button1Click(Sender: TObject);
  private
    { Private 宣言 }
  public
    { Public 宣言 }
  end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

// ************ loggamma(x) ************
const
  N =      8;

  B0 = 1;                 // 以下はBernoulli数
  B1 = (-1.0 / 2.0);
  B2 = ( 1.0 / 6.0);
  B4 = (-1.0 / 30.0);
  B6 = ( 1.0 / 42.0);
  B8 = (-1.0 / 30.0);
  B10 = ( 5.0 / 66.0);
  B12 = (-691.0 / 2730.0);
  B14 = ( 7.0 / 6.0);
  B16 = (-3617.0 / 510.0);


function  loggamma(x : double): double;  // ガンマ関数の対数
var
  LOG_2PI : Double;
  v, w  : Double;
begin
  v := 1;
  while x < N do begin
    v :=  v * x;
    x := x + 1;
  end;
  LOG_2PI := ln(2 * pi);
  w := 1 / (x * x);
  result := ((((((((B16 / (16 * 15))  * w + (B14 / (14 * 13))) * w
	            + (B12 / (12 * 11))) * w + (B10 / (10 *  9))) * w
	            + (B8  / ( 8 *  7))) * w + (B6  / ( 6 *  5))) * w
	            + (B4  / ( 4 *  3))) * w + (B2  / ( 2 *  1))) / x
	            + 0.5 * LOG_2PI - ln(v) - x + (x - 0.5) * ln(x);
end;

//*****************************************************************
// Ix(a,b) 正則ベータ関数を計算します。
// Bx(a,b) 不完全ペーター関数は Ix(a,b) * B(a,b) で計算されます。
//*****************************************************************
function p_beta(x, a, b : double): double;       // 正則ベータ関数
var
  k : integer;
  p1, q1, p2, q2, d, previous : double;
begin
  if a <= 0 then begin
    result :=  MaxDouble;
    exit;
  end;
  if b <= 0 then begin
    if x <  1 then begin
      result := 0;
      exit;
    end;
    if x = 1 then begin
      result := 1;
      exit;
    end;
    result :=  MaxDouble;
    exit;
  end;
  if x > (a + 1) / (a + b + 2) then begin
    result := 1 - p_beta(1 - x, b, a);
    exit;
  end;
  if x <= 0 then begin
    result := 0;
    exit;
  end;
  p1 := 0;
  q1 := 1;
  p2 := exp(a * ln(x) + b * ln(1 - x)
		+ loggamma(a + b) - loggamma(a) - loggamma(b)) / a;
  q2 := 1;
  k := 0;
  while k < 200 do begin
    previous := p2;
    d := - (a + k) * (a + b + k) * x
			/ ((a + 2 * k) * (a + 2 * k + 1));
    p1 := p1 * d + p2;
    q1 := q1 * d + q2;
    inc(k);
    d := k * (b - k) * x / ((a + 2 * k - 1) * (a + 2 * k));
    p2 := p2 * d + p1;
    q2 := q2 * d + q1;
    if q2 = 0 then begin
      p2 := Maxdouble;
      continue;
    end;
    p1 := p1 / q2;
    q1 := q1 / q2;
    p2 := p2 / q2;
    q2 := 1;
    if p2 = previous then begin
      result := p2;
      exit;
    end;
  end;
  Form1.Memo1.Lines.Add('p_beta: 収束しません');
  result := p2;
end;

function q_beta(x, a, b: double): double;
begin
  result := 1 - p_beta(x, a, b);
end;

//**********************************************************/

procedure TForm1.Button1Click(Sender: TObject);
var
  ch   : integer;
  a, b, x : extended;
  Bx, Bi   : extended;
  dx, Bg: double;
  Sg   : string;
begin
  val(LabeledEdit1.Text, a, Ch);
  if ch <> 0 then begin
    MessageDlg('a値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  if a < 0 then begin
    MessageDlg('aの値をゼロより大きくしてください。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  val(LabeledEdit2.Text, b, Ch);
  if ch <> 0 then begin
    MessageDlg('b値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  if b < 0 then begin
    MessageDlg('bの値をゼロより大きくしてください。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  Memo1.Clear;
  val(LabeledEdit3.Text, x, Ch);
  if ch <> 0 then begin
    MessageDlg('x値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  if x < 0 then begin
    MessageDlg('xの値をゼロより大きくしてください。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  if x > 1 then begin
    MessageDlg('xの値をが１より大きいです。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;

  Memo1.Clear;
  {$IFDEF CPUX64}                               // プラットフォーム64ビット
  begin
    Memo1.Lines.Add('X64モード');
  end;
  {$ENDIF CPUX64}
  {$IFDEF CPUX86}                               // プラットフォーム32ビット
  begin
    Memo1.Lines.Add('X86モード');
  end;
  {$ENDIF CPUX86}
  if (a <= 0) or (b <= 0) then begin                  // X Y 0なら
    if a <= 0 then Memo1.Lines.Add('aの値をゼロより大きくしてください。');
    if b <= 0 then Memo1.Lines.Add('bの値をゼロより大きくしてください。');
    exit;
  end;
  Sg := 'Bx(a, b) = ';
  Bx := p_beta(x, a, b);                                        // 正則ベータ関数
  Bi := exp(loggamma(a) + loggamma(b) - loggamma(a + b));       // ペータ関数
  Memo1.Lines.Add(Sg + floatTostrF(Bx * Bi, ffgeneral, 20, 3)); // Bx * Bi 不完全ペーター関数
  Sg := 'Ix(a, b) = ';
  Memo1.Lines.Add(Sg + floatTostrF(Bx, ffgeneral, 20, 3));      // iBの値表示(正則ベータ関数)
  Series1.Clear;
  Series2.Clear;
  Bx := p_beta(x, a, b);
  Bg := Bx * Bi;
  Series2.AddXY(X, Bg);
  dx := 1 / 100;
  for ch := 0 to 100 do begin
    x := dx * ch;
    Bx := p_beta(x, a, b);
    Bg := Bx * Bi;                                              // 不完全ペーター関数
    Series1.AddXY(X, Bg);
  end;
end;

end.

　
　　　incomplete_beta_function.zip

各種プログラム計算例に戻る