ベータ関数
ベータ関数の詳細については、ウィキペディア ベータ関数を参照してください。
ペーター関数は次の定義となっています。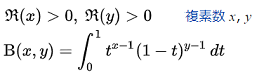
ガンマ関数で表すと次のようになりますので、ガンマ関数からペーター関数を計算するのが一般的なようです。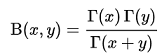
正の整数の場合は、
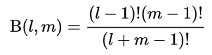
の様になりますが、正の整数のガンマ関数による計算と同じです。
プログラムはガンマ関数のプログラムを使えば計算できるのですが、一応載せておきます。
ガンマ関数にΓ関数を簡単に計算すめプログラムがありその中にペータ関数の計算も入れてあるのでそちらも参照してください。
プログラム
プログラムはMathematics Source Library Beta function.c をDelphi に変換したものです。
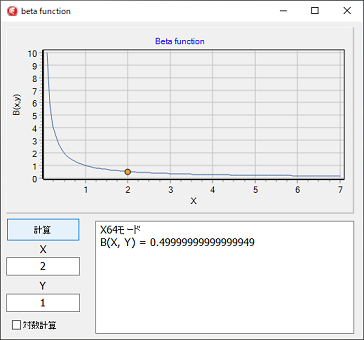左図はβ関数のグラフですが、横軸はXの値です。
対数値も計算可能です。
//============================================================================= // http://www.mymathlib.com/c_source/functions/gamma_beta/gamma_function.c // http://www.mymathlib.com/c_source/functions/gamma_beta/beta_function.c // // ルーチン // Gamma_Function // xGamma_Function // Gamma_Function_Max_Arg // xGamma_Function_Max_Arg // Ln_Gamma_Function(x) // xLn_Gamma_Function(x) // Beta_Function // xBeta_Function // Ln_Beta_Function // xLn_Beta_Function // // 実数x> 0のxのガンマ関数は次のように定義されます。 // Gamma(x)= Integral[0、inf]t^(x-1)exp(-t)dt // 複雑な平面内で解析的に継続され、単純な極がある // 非正の整数、つまりガンマ関数は有理型である // 非正の整数に単純な極を持つ関数。 // 実数x<0の場合、ガンマ関数は反射方程式を満たします。 // Gamma(x)= pi/(sin(pi*x)*Gamma(1-x)) // // 関数Gamma_Function()およびxGamma_Function()はガンマを返します。 // 関数はxでx実数で評価されます。 // // 関数Gamma_Function_Max_Arg()は、最大引数を返します // 引数>1のガンマ関数は、double型の値を返します。 // // 関数xGamma_Function_Max_Arg()は、 // 引数>1のガンマ関数とextended型の戻り値です。 // // Ln_Gamma_Function(x) および xLn_Gamma_Function(x) // // Gamma_Function_Max_Arg = 171とすると、 // 0 < x <= 171の場合、ln(gamma(x))は、Gamma_Function(x)からの結果。 // x> 171の場合、ln(gamma(x)は漸近展開を使用して計算されます。 // ln(gamma(x)〜ln(2sqrt(2pi))-x + (x-1/2)ln x + // B[2j] / [2j *(2j-1)* x^(2j-1)]の合計、 // 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。 // // ベータ関数は被積分関数の0から1までの積分です // x^(a-1)(1-x)^(b-1)、パラメータa>0およびb>0 // ガンマ関数に対して、ベータ関数は次のとおりです： // beta(a,b)= gamma(a)*gamma(b)/gamma(a+b) // // Ln_Beta_Function 及び xLn_Beta_Function // ln(Beta(a、b)=ln(Gamma(a))+ln(Gamma(b))-ln(Gamma(a+b)) //============================================================================= unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart, system.UITypes; type TForm1 = class(TForm) Button1: TButton; LabeledEdit2: TLabeledEdit; Memo1: TMemo; CheckBox1: TCheckBox; LabeledEdit1: TLabeledEdit; Chart1: TChart; Series1: TLineSeries; Series2: TPointSeries; procedure Button1Click(Sender: TObject); Private { Private 宣言 } function Gamma_Function(x: double): double; function xGamma_Function(x: extended): extended; function xGamma(x: extended): extended; function Duplication_Formula(two_x: extended): extended; function Gamma_Function_Max_Arg: double; function xGamma_Function_Max_Arg: extended; function Ln_Gamma_Function(x: double): double; function xLn_Gamma_Function(x: extended): extended; function xLnGamma_Asymptotic_Expansion(x: extended): extended; function Beta_Function(a, b: double): double; function xBeta_Function(a, b: extended): extended; function LnBeta_Function(a, b: double): double; function xLnBeta_Function(a, b: extended): extended; Public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses math; const LONG_MAX = 2147483647; e = 2.71828182845904523536028747; exp_g_o_sqrt_2pi = 6.23316569877722552586386e+3; g = 9.65657815377331589457187; max_double_arg: double = 171.6243769; max_long_double_arg: extended = 1755.5; a: array[0..8] of extended = ( +1.14400529453851095667309e+4, -3.23988020152318335053598e+4, +3.50514523505571666566083e+4, -1.81641309541260702610647e+4, +4.63232990536666818409138e+3, -5.36976777703356780555748e+2, +2.28754473395181007645155e+1, -2.17925748738865115560082e-1, +1.08314836272589368860689e-4 ); //============================================================================= // // この関数はLanczosの式を使用して実際のGamma(x)を計算します。 // xの範囲は -(max_double_arg-1) < x < max_double_arg。 // ガンマ関数は複素平面で有理型であり、 // 正でない整数の値、xaの正の整数または半分の正の整数をテストすると、 // 約1.9e-16の最大絶対相対誤差です。 // x > max_double_argの場合、xGamma_Function(x)を使用する必要があります。 // または lnGamma(x) を計算します。 // x < 0の場合、ln(Gamma(x))は複素数になる可能性があることに注意してください。 // 複素数の計算はプログラムに組んでありません // 戻り値 // xが正で、max_double_argより小さい場合、Gamma(x)は // 返され、x> max_double_argの場合、maxdoubleが返されます。 // xが非正の整数、つまりxが極の場合、maxdoubleが返されます。 // （Gamma(x)は極の両側で符号を変更することに注意してください）。 // xが非正の非整数の場合 Gamma(x)> maxdouble場合、maxdoubleが返され、 // Gamma(x)<-maxdoubleの場合、-maxdoubleが返されます。 // //============================================================================= //================ ガンマ関数 =================== // Γ(x) function TForm1.Gamma_Function(x: double): double; var g: extended; maxx: double; begin maxx := max_double_arg; if x >= maxx then begin result := maxdouble; exit; end; g := xGamma_Function(x); if abs(g) < maxdouble then result := g else if g < 0 then result := -maxdouble else result := maxdouble; end; //============================================================================= // // この関数はLanczosの式を使用して実際のGamma(x)を計算します。 // xの範囲は -(max_long_double_arg-1) < x < max_long_double_arg。 // ガンマ関数は複素平面で有理型であり、正でない整数の値 // xaの正の整数または半分の正の整数をテストすると、 // 最大絶対相対誤差は約3.5e-16です。 // // x > max_long_double_argの場合、lnGamma(x)を使用する必要があります。 // x < 0 の場合、ln(Gamma(x)) は複素数になる可能性があることに注意してください。 // // 戻り値 // xが正で、max_long_double_argより小さい場合、Gamma(x) // が返され、x > max_long_double_argの場合、maxextendedが返されます。 // xが正でない整数の場合、maxextendedが // 返されます（Gamma(x)は値の両側で符号を変更することに注意してください）。 // xが非正の非整数の場合でx>-(max_long_double_arg + 1）の場合 // Gamma(x)が返されます。それ以外の場合は0.0が返されます // //============================================================================= function TForm1.xGamma_Function(x: extended): extended; var sin_x: extended; rg: extended; ix: int64; begin if x > 0 then if x <= max_long_double_arg then begin result := xGamma(x); exit; end else begin result := maxextended; exit; end; if x > -LONG_MAX then begin ix := round(x); if x = ix then begin result := maxextended; exit; end; end; sin_x := sin(pi * x); if sin_x = 0 then begin result := maxextended; exit; end; if x < - max_long_double_arg - 1 then begin result := 0; exit; end; rg := xGamma(1 - x) * sin_x / pi; if rg <> 0 then result := 1 / rg else result := maxextended; end; //============================================================================= // // この関数はLanczosの式を使用して実際のGamma(x)を計算します。 // x、ここで0<x<=900。900<x<1755.5の場合、倍数公式を使用します。 // 関数power()。結果の相対誤差は約10^-16です。x = 0付近を除きます。 // x>1755.5の場合、lnGamma(x)を計算する必要があります。 // xが正で1755.5未満の場合、Gamma(x)が返され、 // x>1755.5の場合、maxextendedが返されます。 // //============================================================================= function TForm1.xGamma(x: extended): extended; var xx: extended; temp: extended; n, i: integer; xx2 : extended; begin if x < 1 then xx := x + 1 else xx := x; n := sizeof(a) div sizeof(extended); if x > max_long_double_arg then begin result := maxextended; exit; end; if x > 900 then begin result := Duplication_Formula(x); exit; end; temp := 0; for i := n - 1 downto 0 do temp := temp + a[i] / (xx + i); temp := temp + 1; xx2 := (xx - 0.5) / 2; temp := temp * (power((g + xx - 0.5) / e, xx2) / exp_g_o_sqrt_2pi ); temp := temp * power((g + xx - 0.5) / e, xx2); // X64 オーバーフロー対策 if x < 1 then result := temp / x else result := temp; end; //============================================================================= // // この関数は倍数公式を使用してGamma(two_x)を返します。 // //============================================================================= function TForm1.Duplication_Formula(two_x: extended): extended; var x: extended; g: extended; n: integer; begin x := 0.5 * two_x; n := round(two_x) - 1; g := power(2.0, two_x - 1.0 - n); g := g * power(2, n); g := g / sqrt(pi); g := g * xGamma_Function(x); g := g * xGamma_Function(x + 0.5); result := g; end; //============================================================================= // // この関数は、Gamma_Functionの最大引数を返します。 // Gamma_Functionは引数が1より大きい場合、< maxdoubleという数値が返されます。 // //============================================================================= function TForm1.Gamma_Function_Max_Arg: double; begin result := max_double_arg; end; //============================================================================= // // この関数は、xGamma_Functionの最大引数を返します。 // xGamma_Functionは引数が1より大きい場合、< maxextendedという数値が返されます。 // //============================================================================= function TForm1.xGamma_Function_Max_Arg: extended; begin result := max_long_double_arg; end; //***************************************************************************** //============================================================================= // // 正の実数xに対するGamma(x)の自然対数を計算します。 // //============================================================================= //============================================================================= // Ln_Gamma_Function(x) および xLn_Gamma_Function(x) // // Gamma_Function_Max_Arg = 171とすると、 // 0 < x <= 171の場合、ln(gamma(x))は、Gamma_Function(x)からの結果。 // x> 171の場合、ln(gamma(x)は漸近展開を使用して計算されます。 // ln(gamma(x)〜ln(2sqrt(2pi))-x + (x-1/2)ln x + // B[2j] / [2j *(2j-1)* x^(2j-1)]の合計、 // 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。 // //============================================================================= function TForm1.Ln_Gamma_Function(x: double): double; begin // 正の引数の 0 <x <= Gamma_Function_Max_Arg // の場合、Log(Gamma(x)を返します。 if x <= Gamma_Function_Max_Arg then result := ln(Gamma_Function(x)) // そうでない場合は、ln Gamma(x) の漸近展開から結果を返します。 else result := xLnGamma_Asymptotic_Expansion(x); end; //============================================================================= // // 正の実数のGamma(x)の自然対数を計算します // // Gamma_Function_Max_Arg = 171とすると、 // 0 <x <= 171の場合、ln(gamma(x))は // Gamma_Function(x)からの結果の値。 // x> 171の場合、ln(gamma(x)) は漸近展開を使用して計算されます。 // ln（gamma(x))〜ln（2sqrt(2pi))-x +(x-1/2)ln x + // B[2j] / [2j *(2j-1)* x^(2j-1)]の合計、 // 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。 // //============================================================================= function TForm1.xLn_Gamma_Function(x: extended): extended; begin // 正の引数の場合、0 <x <= Gamma_Function_Max_Arg() // の場合、LogGamma(x)を返します。 if x <= xGamma_Function_Max_Arg then result := ln(xGamma_Function(x)) // そうでない場合は、ln Gamma(x) の漸近展開から結果を返します。 else result := xLnGamma_Asymptotic_Expansion(x); end; //============================================================================= // // この関数は、漸近を評価することでlog(gamma(x)を推定します // // ln(Gamma(x))〜ln(2sqrt(2pi))-x +(x-1/2)ln(x) + // B[2j] / [2j *（2j-1）* x^(2j-1)]の合計、 // 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。 // //============================================================================= const log_sqrt_2pi = 9.18938533204672741780329736e-1; //ベルヌーイ数B(2)、B(4)、B(6)、...、B(20) B : array[0..9] of extended = ( 1.0 / (6 * 2 * 1), -1.0 / (30 * 4 * 3), 1.0 / (42 * 6 * 5), -1.0 / (30 * 8 * 7), 5.0 / (66 * 10 * 9), -691.0 / (2730 * 12 * 11), 7.0 / (6 * 14 * 13), -3617.0 / (510 * 16 * 15), 43867.0 / (798 * 18 * 17), -174611.0 / (330 * 20 * 19)); n: integer = sizeof(B) div sizeof(extended); function TForm1.xLnGamma_Asymptotic_Expansion(x: extended): extended; //const // m = 3; // 3で十分な精度が得られます。 var i : integer; term: array[0..9] of extended; sum : extended; xx : extended; xj : extended; lngamma : extended; begin sum := 0; xx := x * x; xj := x; lngamma := log_sqrt_2pi - xj + (xj - 0.5) * ln(xj); for i := 0 to n - 1 do begin // for i := 0 to m - 1 do begin term[i] := B[i] / xj; xj := xj * xx; end; for i := n - 1 downto 0 do sum := sum + term[i]; // for i := m - 1 downto 0 do sum := sum + term[i]; result := lngamma + sum; end; //***************************************************************************** const ln_LDBL_MAX : extended = 1.13565234062941435e+4; //============================================================================== // function Beta_Function(a,b : double): double // // この関数は、beta(a、b)=gamma(a)*gamma(b)/gamma(a+b)、を返します // ここでa> 0、b>0 // // 戻り値 // beta（a、b）が返されます // beta（a、b）がDBL_MAXを超える場合は、DBL_MAXが返されます //============================================================================== function TForm1.Beta_Function(a, b: double): double; var beta : extended; begin beta := xBeta_Function(a, b); if beta < MAXDouble then result := beta else result := MAXDouble; end; //============================================================================== // function xBeta_Function(a,b: extended): extended // //この関数は、beta(a,b)=gamma(a)*gamma(b)/gamma(a+b) を返します // a> 0、b>0 // // 引数 // ベータ関数の引数をextendedにします // a,bは正でなければなりません // //戻り値 // beta（a、b）が返されます。// // beta（a、b）がextendedを超える場合は、extendedが返されます // //============================================================================== function TForm1.xBeta_Function(a, b: extended): extended; var lnbeta : extended; begin // If (a + b) <= Gamma_Function_Max_Arg() then simply return // gamma(a)*gamma(b) / gamma(a+b). if (a + b) <= Gamma_Function_Max_Arg then begin result := xGamma_Function(a) / (xGamma_Function(a + b) / xGamma_Function(b)); exit; end; // If (a + b) > Gamma_Function_Max_Arg() then simply return // exp(lngamma(a) + lngamma(b) - lngamma(a+b) ). lnbeta := xLn_Gamma_Function(a) + xLn_Gamma_Function(b) - xLn_Gamma_Function(a + b); if lnbeta > ln_LDBL_MAX then result := MAXExtended else result := exp(lnbeta); end; //============================================================================= // function Ln_Beta_Function(a,b: double): double; // // この関数は、ln(Beta(a,b))を返します // ここで、a> 0およびb> 0です // // 戻り値 // log(beta(a、b)) // //============================================================================= function TForm1.LnBeta_Function(a, b: double): double; begin result := xLnBeta_Function(a, b); end; //============================================================================= // function xLn_Beta_Function(a,b: extended): extended; // // この関数は、ln(Beta(a,b))を返します // ここで、a> 0およびb> 0です // // 戻り値 // log(beta(a、b)) // //============================================================================= function TForm1.xLnBeta_Function(a, b: extended): extended; begin // If (a + b) <= Gamma_Function_Max_Arg then simply return // log(gamma(a)*gamma(b) / gamma(a+b)). if a + b <= Gamma_Function_Max_Arg then begin if (a = 1.0) and (b = 1) then result := 0.0 else result := ln( xGamma_Function(a) / (xGamma_Function(a + b) / xGamma_Function(b))); exit; end; // If (a + b) > Gamma_Function_Max_Arg() then simply return // lngamma(a) + lngamma(b) - lngamma(a+b). result := xLn_Gamma_Function(a) + xLn_Gamma_Function(b) - xLn_Gamma_Function(a+b); end; //============================================================================= // beta関数計算 // a, bの値は a>0 b>0 の範囲です。 // 入力されたa, b の値でbata関数を計算し、グラフのbata曲線上にプロットします。 //============================================================================= procedure TForm1.Button1Click(Sender: TObject); const GLIMIT = 100; // グラフデーター上下限値 グラフ値のオーバーフロー防止数 PLIMIT = 11.3; // グラフ点プロットの上下限値点の半分を表示 ALIMIT = 10.5; // 通常Γ値グラフ左軸スケール上下値 MINARG = 5.5626846463e-309; // 下限値 0 < x MINARG でオーバーフロー var ch : integer; X, Y, B : extended; maxarg0: extended; Sg : string; istr : string; X8664F : boolean; // true 86 false 64 MIN, MAX : double; dx : double; begin val(LabeledEdit1.Text, X, Ch); if ch <> 0 then begin MessageDlg('X値に間違いがあります。', mtInformation, [mbOk], 0, mbOk); exit; end; if X < 0 then begin MessageDlg('Xの値をゼロより大きくしてください。', mtInformation, [mbOk], 0, mbOk); exit; end; val(LabeledEdit2.Text, Y, Ch); if ch <> 0 then begin MessageDlg('Y値に間違いがあります。', mtInformation, [mbOk], 0, mbOk); exit; end; if Y < 0 then begin MessageDlg('Yの値をゼロより大きくしてください。', mtInformation, [mbOk], 0, mbOk); exit; end; Memo1.Clear; Sg := 'B(X, Y) = '; if checkbox1.Checked = true then begin Sg := 'LnB(X, Y) = '; end; {$IFDEF CPUX64} // プラットフォーム64ビット begin X8664F := False; Memo1.Lines.Add('X64モード'); end; {$ENDIF CPUX64} {$IFDEF CPUX86} // プラットフォーム32ビット begin X8664F := True; Memo1.Lines.Add('X86モード'); end; {$ENDIF CPUX86} if X8664F then maxarg0 := xGamma_Function_Max_Arg // ガンマ計算の最大値 else maxarg0 := Gamma_Function_Max_Arg; if (X + Y) > maxarg0 then begin // 計算の最大値チェック Memo1.Lines.Add('入力値が計算最大値を超えています。'); exit; end; if (X <= 0) or (Y <= 0) then begin // X Y 0なら if X <= 0 then Memo1.Lines.Add('Xの値をゼロより大きくしてください。'); if Y <= 0 then Memo1.Lines.Add('Yの値をゼロより大きくしてください。'); if checkbox1.Checked = false then Memo1.Lines.Add(Sg + '1') else begin Memo1.Lines.Add(Sg + '0'); end; exit; end else begin if checkbox1.Checked = False then begin // 非対数なら if X8664F then B := xBeta_Function(x, y) else B := Beta_Function(x, y); end else // 対数なら if X8664F then B := xLnBeta_Function(x, y) // 対数ペーター else B := LnBeta_Function(x, y) end; Memo1.Lines.Add(Sg + floatTostrF(B, ffgeneral, 20, 3) + istr); // Bの値表示 Series1.Clear; Series2.Clear; Series2.AddXY(x, B); MIN := x / 20; MAX := x + 5; dx := (MAX - MIN) / 100; for ch := 0 to 100 do begin x := dx * ch + MIN; if checkbox1.Checked = False then B := Beta_Function(x, y) // 非対数なら else B := LnBeta_Function(x, y); Series1.AddXY(x, B); end; end; end.
beta_function.zip