
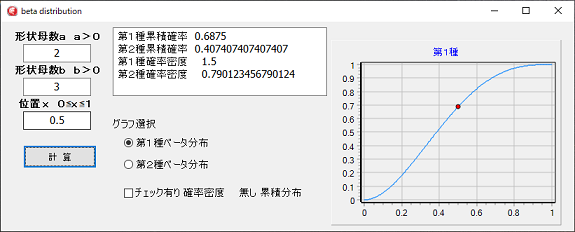
ベータ分布
連続確率分布で第1種と第2種があります。
単にベータ分布と呼ぶ場合は第1種ペーター分布です。

プログラム
プログラムはMathematics Source Library C & ASMにあった不完全ベータ関数を使用していますが、
C言語辞典アルゴリズムにあるものを利用すればプログラムは簡単になります。
Delphi用に変換したものが不完全ベータ関数にあるので参照してください。
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, system.Math, Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons,
system.UITypes, VclTee.TeeGDIPlus, VCLTee.Series, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart;
type
TForm1 = class(TForm)
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
Memo1: TMemo;
BitBtn1: TBitBtn;
RadioButton1: TRadioButton;
RadioButton2: TRadioButton;
Label1: TLabel;
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
CheckBox1: TCheckBox;
procedure FormCreate(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
procedure RadioButton2Click(Sender: TObject);
procedure RadioButton1Click(Sender: TObject);
private
{ Private 宣言 }
function xBeta_Function(a, b: extended): extended;
function Gamma_Function_Max_Arg: double;
function xGamma_Function(x: extended): extended;
function xLn_Gamma_Function(x: extended): extended;
function xGamma(x: extended): extended;
function xGamma_Function_Max_Arg: extended;
function xLnGamma_Asymptotic_Expansion(x: extended): extended;
function Duplication_Formula(two_x: extended): extended;
function Beta_Distribution(x, a, b: double): double;
function xBeta_Distribution(xx, aa, bb: double): extended;
function Beta_Continued_Fraction(x, a, b: extended): extended;
function Beta_Function(a, b: double): double;
function Beta_Density(x, a, b: double): double;
function Beta_Density2(x, a, b: double): double;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
//===============================================================================
// function Beta_Density(x, a, b)
//
// 説明:
// 第1種ベータ分布の密度は
// x <0の場合は0
// 0 <= x <= 1 f(x) = x^(a-1) (1-x)^(b-1) / B(a,b)
// x> 1の場合は0
// ここで、a>0, b>0, B(a,b)は完全ベータ関数です
//
// 引数:
// x: double
// 密度関数の引数。x <= 0の場合、結果は0であり、x> = 1の場合も結果は0、
// それ以外の場合
// a <1 又は x = 1, x = 0の場合を除き、上記の関数です
// b <1の場合はMaxDoubleが返されます。
// a: double ベータ分布の正の形状パラメータ、
// a-1は、被積分関数の係数xの指数です。
// b: double ベータ分布の正の形状パラメータ、
// b-1は、被積分関数の係数(1-x)の指数です。
//
//===============================================================================
function TForm1.Beta_Density(x, a, b: double): double;
begin
result := 0;
if (x <= 0.0) or (x >= 1.0) then exit;;
result := power(x, a - 1.0) * power(1.0 - x, b - 1.0) / Beta_Function(a,b);
end;
//===============================================================================
// function Beta_Density2(x, a, b)
//
// 説明:
// 第2種ベータ分布の密度は
// x <0の場合は0
// 0 <= x f(x) = x^(a-1) (1+x)^(-a-b) / B(a,b)
// x> 1の場合は0
// ここで、a>0, b>0, B(a,b)は完全ベータ関数です
//
// 引数:
// x: double
// 密度関数の引数。x <= 0の場合、結果は0、
// それ以外の場合
// a: double ベータ分布の正の形状パラメータ、
// a-1は、被積分関数の係数xの指数です。
// b: double ベータ分布の正の形状パラメータ、
// b-1は、被積分関数の係数(1-x)の指数です。
//
//===============================================================================
function TForm1.Beta_Density2(x, a, b: double): double;
begin
result := 0;
if x < 0.0 then exit;;
result := power(x, a - 1.0) * power(1.0 + x, -a - b) / Beta_Function(a,b);
end;
//===============================================================================
// function Beta_Function(a, b: double): double;
//
// 説明:
// この関数は beta(a,b) = gamma(a)*gamma(b)/gamma(a+b)を返します。
// ここで a>0, b>0
//
// 引数:
// a : double 引数は正でなければなりません。
// b : double 引数は正でなければなりません。
//
//===============================================================================
function TForm1.Beta_Function(a, b: double): double;
var
beta: extended;
begin
beta := xBeta_Function(a, b);
if beta < MaxDouble then result := beta
else result := MaxDouble;
end;
//================================================================================
// function Beta_Distribution(x,a,b: double): double;
//
// 説明:
// ベータ分布は-infからxまでの積分です。
// t <= 0 の場合は 0
// 0 <t <1 の場合、t^(a-1)(1-t)^(b-1)/ B(a,b)
// t> = 1 の場合は 0
// a> 0, b> 0, B(a,b)は(完全な)ベータ関数です。
//
// 0 <x <1の場合、ベータ分布を評価するための手順は
// ベータ分布の継続的な分数展開:
// beta(x,a,b)= [x^a *(1-x^b /(a B(a,b))]
// *((1/1+)(d[1]/1+)(d[2]/1+)...)
// ここで d[2m+1] = - (a+m)(a+b+m)x/((a+2m)(a+2m+1))
// d[2m] = m(b-m)x/((a+2m)(a+2m-1)).
// 対称関係:
// beta(x,a,b)= 1 - beta(1-x,b,a).
// 繰り返し関係:
// beta(x,a+1,b) = beta(x,a,b+1) - x^a(1-x)^b / (b*B(a+1,b)).
// beta(x,a,b+1) = beta(x,a+1,b) + x^a(1-x^ b /(a*B(a,b+1)).
// そして相互関係:
// beta(x,a,b) = [a * beta(x,a+1,b)+ b*beta(x,a,b+1)] / (a+b).
//
// a > 1 と b > 1の両方の場合で
// x <=(a-1)/(a+b-2)の場合、
// 継続分数展開を使用します でなければ
// 対称関係を使用し、継続部分を使用します。
// beta(1-x,b,a)を評価するための拡張です。
//
// a < 1 及び b > 1の場合、
// 相互関係式を再帰と共に使用します
// 評価する関係
// beta(x,a,b) = beta(x,a+1,b)+ [x^a*(1-x)^b] / [a * B(a,b)].
//
// a> 1 かつ b <1の場合、
// 相互関係式を再帰と共に使用します
// 評価する関係
// beta(x,a,b) = beta(x,a,b+1)-[x^a*(1-x)^b] / [b * B(a,b)].
//
// a <1 及び b<1の場合、
// 相互関係式を使用して評価します
// beta(x,a,b)= [a * beta(x,a+1,b)+ b * beta(x,a,b+1)] / (a+b)
// 現在は1つの形状パラメーター > 1 を持つベータ分布の観点から
//
// a == 1の場合、積分を明示的に評価します
// beta(x,a,b)= [1-(1-x)^b] / [b*B(a,b].
//
// b == 1の場合、積分を明示的に評価します
// beta(x,a,b)= x^a / [a* B(a,b)].
//
//
// 引数:
// x : double ベータ分布の引数 x <= 0の場合、結果は0であり、
// x >= 1の場合、結果は1、それ以外の場合、結果は上記の積分です。
// a: double ベータ分布の正の形状パラメーター
// a-1 は、被積分関数の係数xの指数です。
// b: double ベータ分布の正の形状パラメーター
// b-1は、被積分関数の係数(1-x)の指数です。
//
// 戻り値:
// 0〜1の実数。
//===============================================================================
function TForm1.Beta_Distribution(x, a, b: double): double;
begin
result := 0;
if x <= 0.0 then result := 0.0;
if x >= 1.0 then result := 1.0;
if (x <= 0) or (x >= 1) then exit;
result := xBeta_Distribution(x, a, b);
end;
//===============================================================================
// function xBeta_Distribution(x,a,b: double): extended;
//
// 説明:
// 不完全ベータ関数は t^(a-1)(1-t^(b-1)dt の 0からx 迄の積分です。
// ここで、0 <= x <= 1、a> 0, b> 0 です。
//
// 不完全ベータ関数を評価する手順では、
// 不完全ベータ関数の継続的な分数展開:
// beta(x,a,b)= x^a *(1-x)^b / a *((1/1+)(d[1] / 1+)(d[2] / 1+)...)
// ここで d[2m+1] = - (a+m)(a+b+m)x/((a+2m)(a+2m+1))
// d[2m] = m(b-m)x/((a+2m)(a+2m-1)).
// 対称関係:
// beta(x,a,b)= B(a,b)-beta(1-x,b,a)
// B(a,b)は完全ベータ関数です。
// 繰り返し関係:
// beta(x,a+1,b)= a/b beta(x,a,b+1)-x^a (1-x)^b /b
// beta(x,a,b+1)= b/a beta(x,a+1,b)+x^a(1-x)^b /a.
// そして相互関係:
// beta(x,a,b)= beta(x,a+1,b)+beta(x,a,b+1).
//
// a> 1とb> 1 両方の場合、
// x <=(a-1)/(a+ b-2)の場合
// 継続分数展開を使用します
// でなければ
// 対称関係を使用し、継続部分を使用します
// beta(1-x,b,a)を評価するための拡張です。
//
// a <1 及び b> 1の場合、
// 相互関係式を再帰と共に使用します
// 評価する関係
// beta(x,a,b)= [(a+b) beta(x,a+1,b+x^a(1-x)^b] / a.
//
// a> 1 かつ b <1の場合、
// 相互関係式を再帰と共に使用します
// 評価する関係
// beta(x,a,b)= [(a+b)beta(x,a,b+1)-x^a(1-x)^b] / b.
//
// a <1 及び b <1の場合、
// 相互関係式を使用して評価します
// beta(x,a,b)= beta(x,a+1,b)+beta(x,a,b+1)
// 1つの形状パラメータ> 1を持つベータ関数に関して
//
// a == 1 の場合、積分を明示的に評価します
// beta(x,a,b)= [1-(1-x)^b] / b.
//
// b == 1 の場合、積分を明示的に評価します
// beta(x,a,b)= x^a /a.
//
//
// 引数://
// x: extended 不完全ベータ関数積分の上限
// xは閉じた間隔[0,1]内にある必要があります。
// a: extended 不完全ベータ関数のShapeパラメータ, a-1
// 被積分関数の係数xの指数です。
// b: extebded 不完全ベータ関数のShapeパラメータ, b-1
// 被積分関数の係数(1-x)の指数です。
//
// 戻り値:
// beta(x,a,b): extended;
//
//===============================================================================
function TForm1.xBeta_Distribution(xx, aa, bb: double): extended;
var
x, a, b: extended;
begin
x := xx;
a := aa;
b := bb;
// Both shape parameters are strictly greater than 1.
if (aa > 1.0) and (bb > 1.0) then begin
if (x <= (a - 1.0) / ( a + b - 2.0)) then
result := Beta_Continued_Fraction(x, a, b)
else
result := 1.0 - Beta_Continued_Fraction(1.0 - x, b, a);
exit;
end;
// Both shape parameters are strictly less than 1.
if (aa < 1.0) and (bb < 1.0) then begin
result := (a * xBeta_Distribution(xx, aa + 1.0, bb)
+ b * xBeta_Distribution(xx, aa, bb + 1.0) ) / (a + b);
exit;
end;
// One of the shape parameters exactly equals 1.
if aa = 1.0 then begin
result := 1.0 - power(1.0 - x, b) / (b * xBeta_Function(a, b));
exit;
end;
if bb = 1.0 then begin
result := power(x, a) / (a * xBeta_Function(a, b));
exit;
end;
// Exactly one of the shape parameters is strictly less than 1.
if aa < 1.0 then begin
result := xBeta_Distribution(xx, aa + 1.0, bb)
+ power(x, a) * power(1.0 - x, b) / (a * xBeta_Function(a,b));
exit;
end;
// The remaining condition is b < 1.0
result := xBeta_Distribution(xx, aa, bb + 1.0)
- power(x, a) * power(1.0 - x, b) / (b * xBeta_Function(a, b));
end;
//===============================================================================
// function Beta_Continued_Fraction(x, a, b: extended): extended
//
// 説明:
// 不完全ベータを評価するために使用される継続的な分数展開
// 関数は
// beta(x,a,b)= x^a*(1-x)^b / a*((1/1+)(d[1]/1+)(d[2]/1+)...)
// ここで d[2m+1] = - (a+m)(a+b+m)x / ((a+2m)(a+2m+1))
// d[2m] = m(bm)x / ((a+2m)(a+2m-1)).
//
// ここで, a>1, b>1, 及び x <= (a-1) / (a+b-2)です。
//
// 引数:
// x: extended 不完全ベータ関数積分の上限
// xは閉じた間隔[0,1]内にある必要があります。
// a: extended 不完全ベータ関数のShapeパラメータ a-1
// 被積分関数の係数xの指数です。
// b: extended 不完全ベータ関数のShapeパラメータ b-1
// 被積分関数の係数(1-x)の指数です。
//
// 戻り値:
// beta(x,a,b)
//
//===============================================================================
var
LDBL_EPSILON: extended;
function TForm1.Beta_Continued_Fraction(x, a, b: extended): extended;
var
Am1, A0, Bm1, B0: extended;
e: extended;
Ap1, Bp1: extended;
f_less: extended;
f_greater: extended;
aj, am: extended;
eps: extended;
j, m, k: integer;
begin
Am1 := 1.0;
A0 := 0.0;
Bm1 := 0.0;
B0 := 1.0;
e := 1.0;
Ap1 := A0 + e * Am1;
Bp1 := B0 + e * Bm1;
f_less := Ap1 / Bp1;
f_greater := 0.0;
aj := a;
eps := 10.0 * LDBL_EPSILON;
j := 0;
m := 0;
k := 1;
if x = 0.0 then begin
result := 0.0;
exit;
end;
while 2.0 * abs(f_greater - f_less) > eps * abs(f_greater + f_less) do begin
Am1 := A0;
A0 := Ap1;
Bm1 := B0;
B0 := Bp1;
am := a + m;
e := - am * (am + b) * x / ( (aj + 1.0) * aj );
Ap1 := A0 + e * Am1;
Bp1 := B0 + e * Bm1;
k := (k + 1) and 3;
if k = 1 then f_less := Ap1/Bp1
else if k = 3 then f_greater := Ap1/Bp1;
if abs(Bp1) > 1.0 then begin
Am1 := A0 / Bp1;
A0 := Ap1 / Bp1;
Bm1 := B0 / Bp1;
B0 := 1.0;
end
else begin
Am1 := A0;
A0 := Ap1;
Bm1 := B0;
B0 := Bp1;
end;
inc(m);
j := j + 2;
aj := a + j;
e := m * ( b - m ) * x / ( ( aj - 1.0) * aj );
Ap1 := A0 + e * Am1;
Bp1 := B0 + e * Bm1;
k := (k + 1) and 3;
if k = 1 then f_less := Ap1 / Bp1
else if k = 3 then f_greater := Ap1 / Bp1;
end;
result := exp(a * ln(x) + b * ln(1.0 - x) + ln(Ap1 / Bp1)) /
(a * xBeta_Function(a,b));
end;
//===================================================================================
const
LONG_MAX = 2147483647;
e = 2.71828182845904523536028747;
exp_g_o_sqrt_2pi = 6.23316569877722552586386e+3;
g = 9.65657815377331589457187;
ln_LDBL_MAX : extended = 1.13565234062941435e+4;
max_double_arg: double = 171.6243769;
max_long_double_arg: extended = 1755.5;
a: array[0..8] of extended = (
+1.14400529453851095667309e+4,
-3.23988020152318335053598e+4,
+3.50514523505571666566083e+4,
-1.81641309541260702610647e+4,
+4.63232990536666818409138e+3,
-5.36976777703356780555748e+2,
+2.28754473395181007645155e+1,
-2.17925748738865115560082e-1,
+1.08314836272589368860689e-4
);
//==============================================================================
// function xBeta_Function(a,b: extended): extended
//
//この関数は、beta(a,b)=gamma(a)*gamma(b)/gamma(a+b) を返します
// a> 0、b>0
//
// 引数
// ベータ関数の引数をextendedにします
// a,bは正でなければなりません
//
//戻り値
// beta(a、b)が返されます。//
// beta(a、b)がextendedを超える場合は、extendedが返されます
//
//==============================================================================
function TForm1.xBeta_Function(a, b: extended): extended;
var
lnbeta : extended;
begin
// If (a + b) <= Gamma_Function_Max_Arg() then simply return
// gamma(a)*gamma(b) / gamma(a+b).
if (a + b) <= Gamma_Function_Max_Arg then begin
result := xGamma_Function(a) / (xGamma_Function(a + b) / xGamma_Function(b));
exit;
end;
// If (a + b) > Gamma_Function_Max_Arg() then simply return
// exp(lngamma(a) + lngamma(b) - lngamma(a+b) ).
lnbeta := xLn_Gamma_Function(a) + xLn_Gamma_Function(b)
- xLn_Gamma_Function(a + b);
if lnbeta > ln_LDBL_MAX then result := MAXExtended
else result := exp(lnbeta);
end;
//=============================================================================
//
// この関数は、Gamma_Functionの最大引数を返します。
// Gamma_Functionは引数が1より大きい場合、< maxdoubleという数値が返されます。
//
//=============================================================================
function TForm1.Gamma_Function_Max_Arg: double;
begin
result := max_double_arg;
end;
//=============================================================================
//
// この関数はLanczosの式を使用して実際のGamma(x)を計算します。
// xの範囲は -(max_long_double_arg-1) < x < max_long_double_arg。
// ガンマ関数は複素平面で有理型であり、正でない整数の値
// xaの正の整数または半分の正の整数をテストすると、
// 最大絶対相対誤差は約3.5e-16です。
//
// x > max_long_double_argの場合、lnGamma(x)を使用する必要があります。
// x < 0 の場合、ln(Gamma(x)) は複素数になる可能性があることに注意してください。
//
// 戻り値
// xが正で、max_long_double_argより小さい場合、Gamma(x)
// が返され、x > max_long_double_argの場合、maxextendedが返されます。
// xが正でない整数の場合、maxextendedが
// 返されます(Gamma(x)は値の両側で符号を変更することに注意してください)。
// xが非正の非整数の場合でx>-(max_long_double_arg + 1)の場合
// Gamma(x)が返されます。それ以外の場合は0.0が返されます
//
//=============================================================================
function TForm1.xGamma_Function(x: extended): extended;
var
sin_x: extended;
rg: extended;
ix: int64;
begin
if x > 0 then
if x <= max_long_double_arg then begin
result := xGamma(x);
exit;
end
else begin
result := maxextended;
exit;
end;
if x > -LONG_MAX then begin
ix := round(x);
if x = ix then begin
result := maxextended;
exit;
end;
end;
sin_x := sin(pi * x);
if sin_x = 0 then begin
result := maxextended;
exit;
end;
if x < - max_long_double_arg - 1 then begin
result := 0;
exit;
end;
rg := xGamma(1 - x) * sin_x / pi;
if rg <> 0 then result := 1 / rg
else result := maxextended;
end;
//=============================================================================
//
// 正の実数のGamma(x)の自然対数を計算します
//
// Gamma_Function_Max_Arg = 171とすると、
// 0 <x <= 171の場合、ln(gamma(x))は
// Gamma_Function(x)からの結果の値。
// x> 171の場合、ln(gamma(x)) は漸近展開を使用して計算されます。
// ln(gamma(x))〜ln(2sqrt(2pi))-x +(x-1/2)ln x +
// B[2j] / [2j *(2j-1)* x^(2j-1)]の合計、
// 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。
//
//=============================================================================
function TForm1.xLn_Gamma_Function(x: extended): extended;
begin
// 正の引数の場合、0 <x <= Gamma_Function_Max_Arg()
// の場合、LogGamma(x)を返します。
if x <= xGamma_Function_Max_Arg then result := ln(xGamma_Function(x))
// そうでない場合は、ln Gamma(x) の漸近展開から結果を返します。
else
result := xLnGamma_Asymptotic_Expansion(x);
end;
//=============================================================================
//
// この関数はLanczosの式を使用して実際のGamma(x)を計算します。
// x、ここで0<x<=900。900<x<1755.5の場合、倍数公式を使用します。
// 関数power()。結果の相対誤差は約10^-16です。x = 0付近を除きます。
// x>1755.5の場合、lnGamma(x)を計算する必要があります。
// xが正で1755.5未満の場合、Gamma(x)が返され、
// x>1755.5の場合、maxextendedが返されます。
//
//=============================================================================
function TForm1.xGamma(x: extended): extended;
var
xx: extended;
temp: extended;
n, i: integer;
xx2 : extended;
begin
if x < 1 then xx := x + 1 else xx := x;
n := sizeof(a) div sizeof(extended);
if x > max_long_double_arg then begin
result := maxextended;
exit;
end;
if x > 900 then begin
result := Duplication_Formula(x);
exit;
end;
temp := 0;
for i := n - 1 downto 0 do temp := temp + a[i] / (xx + i);
temp := temp + 1;
xx2 := (xx - 0.5) / 2;
temp := temp * (power((g + xx - 0.5) / e, xx2) / exp_g_o_sqrt_2pi );
temp := temp * power((g + xx - 0.5) / e, xx2); // X64 オーバーフロー対策
if x < 1 then result := temp / x
else result := temp;
end;
//=============================================================================
//
// この関数は、xGamma_Functionの最大引数を返します。
// xGamma_Functionは引数が1より大きい場合、< maxextendedという数値が返されます。
//
//=============================================================================
function TForm1.xGamma_Function_Max_Arg: extended;
begin
result := max_long_double_arg;
end;
//=============================================================================
//
// この関数は、漸近を評価することでlog(gamma(x)を推定します
//
// ln(Gamma(x))〜ln(2sqrt(2pi))-x +(x-1/2)ln(x) +
// B[2j] / [2j *(2j-1)* x^(2j-1)]の合計、
// 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。
//
//=============================================================================
const
log_sqrt_2pi = 9.18938533204672741780329736e-1;
//ベルヌーイ数B(2)、B(4)、B(6)、...、B(20)
B : array[0..9] of extended = ( 1.0 / (6 * 2 * 1),
-1.0 / (30 * 4 * 3),
1.0 / (42 * 6 * 5),
-1.0 / (30 * 8 * 7),
5.0 / (66 * 10 * 9),
-691.0 / (2730 * 12 * 11),
7.0 / (6 * 14 * 13),
-3617.0 / (510 * 16 * 15),
43867.0 / (798 * 18 * 17),
-174611.0 / (330 * 20 * 19));
n: integer = sizeof(B) div sizeof(extended);
function TForm1.xLnGamma_Asymptotic_Expansion(x: extended): extended;
//const
// m = 3; // 3で十分な精度が得られます。
var
i : integer;
term: array[0..9] of extended;
sum : extended;
xx : extended;
xj : extended;
lngamma : extended;
begin
sum := 0;
xx := x * x;
xj := x;
lngamma := log_sqrt_2pi - xj + (xj - 0.5) * ln(xj);
for i := 0 to n - 1 do begin
// for i := 0 to m - 1 do begin
term[i] := B[i] / xj;
xj := xj * xx;
end;
for i := n - 1 downto 0 do sum := sum + term[i];
// for i := m - 1 downto 0 do sum := sum + term[i];
result := lngamma + sum;
end;
//*****************************************************************************
//=============================================================================
//
// この関数は倍数公式を使用してGamma(two_x)を返します。
//
//=============================================================================
function TForm1.Duplication_Formula(two_x: extended): extended;
var
x: extended;
g: extended;
n: integer;
begin
x := 0.5 * two_x;
n := round(two_x) - 1;
g := power(2.0, two_x - 1.0 - n);
g := g * power(2, n);
g := g / sqrt(pi);
g := g * xGamma_Function(x);
g := g * xGamma_Function(x + 0.5);
result := g;
end;
//===================================================
//
// プログラム起動時の設定
// EPSILONの値の設定
//
//===================================================
procedure TForm1.FormCreate(Sender: TObject);
var
x, y, s : extended;
begin
s := 1;
x := 1;
repeat
y := 1;
s := s / 2;
y := y + s;
until x = y;
LDBL_EPSILON := s * 2;
Memo1.Clear;
Memo1.Lines.Add('第1種ベータ分布')
end;
//=========================================================
//
// 計算の選択と実行
//
//=========================================================
procedure TForm1.BitBtn1Click(Sender: TObject);
var
a, b, x: double;
bf1, bf2: double;
bd1, bd2: double;
ch: integer;
dx : double;
begin
val(labelededit1.Text, a, ch);
if ch <> 0 then begin
MessageDlg('形状母数a値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
if a <= 0 then begin
MessageDlg('形状母数aの値をゼロより大きくしてください。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
val(labelededit2.Text, b, ch);
if ch <> 0 then begin
MessageDlg('形状母数b値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
if b <= 0 then begin
MessageDlg('形状母数bの値をゼロより大きくしてください。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
val(labelededit3.Text, x, ch);
if ch <> 0 then begin
MessageDlg('位置x値に間違いがあります。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
if radiobutton1.Checked = true then begin
if (0 > x) or (x > 1) then begin
MessageDlg('第1種ベータ分布の場合' + #13#10 + 'xの値は 0 ≦ x ≦ 1 にして下さい。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
end
else begin
if 0 > x then begin
MessageDlg('xの値は 0 ≦ x にして下さい。', mtInformation, [mbOk], 0, mbOk);
exit;
end;
end;
bd1 := Beta_Distribution(x, a, b);
memo1.Clear;
if x > 1 then
memo1.Lines.Add('第1種累積確率 xが1以上値無し')
else
memo1.Lines.Add('第1種累積確率 ' + floatTostr(bd1));
bd2 := Beta_Distribution(x / (1 + x), a, b);
memo1.Lines.Add('第2種累積確率 ' + floatTostr(bd2));
bf1 := Beta_Density(x, a, b);
if x > 1 then
memo1.Lines.Add('第1種確率密度 xが1以上値無し')
else
memo1.Lines.Add('第1種確率密度 ' + floatTostr(bf1));
bf2 := Beta_Density2(x, a, b);
memo1.Lines.Add('第2種確率密度 ' + floatTostr(bf2));
Series1.Clear;
Series2.Clear;
dx := 0;
chart1.Title.Text.Clear;
if radiobutton1.Checked = true then begin
dx := bd1;
chart1.Title.Text.Add('第1種');
end;
if radiobutton2.Checked = true then begin
dx := bd2;
chart1.Title.Text.Add('第2種');
end;
if (CheckBox1.Checked = true) then begin
if radiobutton1.Checked = true then dx := bf1;
if radiobutton2.Checked = true then dx := bf2;
end;
Series2.AddXY(x, dx);
dx := 1 / 200;
if radiobutton2.Checked = true then begin
if x <= 5 then dx := 5 / 200
else dx := round(x + 0.5) / 200;
end;
for ch := 0 to 200 do begin
x := dx * ch;
if CheckBox1.Checked = False then begin
if radiobutton1.Checked = true then bd1 := Beta_Distribution(x, a, b);
if radiobutton2.Checked = true then bd1 := Beta_Distribution(x / (1 + x), a, b);
Series1.AddXY(x, bd1);
end
else begin
if radiobutton1.Checked = true then bf1 := Beta_Density(x, a, b);
if radiobutton2.Checked = true then bf1 := Beta_Density2(x, a, b);
Series1.AddXY(x, bf1);
end;
end;
end;
//========================================================
// 計算の種類変更による表示変更
//========================================================
procedure TForm1.RadioButton1Click(Sender: TObject);
begin
labelededit3.EditLabel.Caption := '位置 x 0≦X≦1 ';
Series1.Clear;
Series2.Clear;
end;
procedure TForm1.RadioButton2Click(Sender: TObject);
begin
labelededit3.EditLabel.Caption := '位置 x 0 ≦ X ';
Series1.Clear;
Series2.Clear;
end;
end.